下凹形态裂隙面粗糙程度表征及立方定律修正系数拟合
甘 磊,马洪影,沈振中
(河海大学 水利水电学院,江苏 南京 210098)
1 研究背景
天然裂隙的裂隙面多为粗糙面,而裂隙面的粗糙程度直接影响裂隙岩体的渗流过程。粗糙裂隙渗流特性不能忽视裂隙面几何特征的影响[1-3]。定量解析和描述裂隙粗糙程度对裂隙渗流水力特性的影响是研究裂隙渗流特性的基础,具有重要意义和价值[4-6]。
粗糙度是结构面侧壁的粗糙程度,是裂隙渗流计算中的关键指标之一。目前,裂隙面粗糙程度信息测定设备主要有测针式剖面测量仪(精度0.1 mm)、断面测量仪(精度10 ~0.001 mm)、千分表(精度0.001 mm)、光投射仪及激光剖面测量仪(精度0.01 μm)等。裂隙粗糙程度表征方法可归纳为三大类:凸起高度表征法、节理粗糙度系数JRC 表征法和分数维表征法[7]。凸起高度表征法直接以裂隙表面的凸起高度函数或凸起高度的概率密度函数来描述裂隙表面的粗糙性,该方法需精确量测裂隙上每一测点凸起高度。JRC 系数一般采用标准剖面对照法确定,但是实际结构面很复杂,难用Barton[8]提出的10 条标准剖面完全表述。分数维表征法是采用分数维的大小来表征裂隙的粗糙程度,主要通过量轨法或功率谱密度法进行测定,近年来应用广泛。如王来贵等[9]利用激光共聚焦显微镜观测不同粒径砂岩裂隙表面,以三维分形维数D作为裂隙表面粗糙度表征参数,建立基于三维分形维数D的单裂隙渗流模型。鞠杨等[10]采用Weierstrass-Mandelbrot 分形函数,基于透明有机玻璃材料制作不同分形维数粗糙单裂隙的物理模型,分析水渗流性质随裂隙粗糙性的变化规律,提出了粗糙单裂隙分形等效渗透系数计算公式。Chen 等[11]利用投影覆盖法计算表面分形维数,采用多重分形参数来表征三维粗糙度。Liren 等[12]引入粗糙度参数,结合分形理论,提出了一种能反映岩石节理剪切强度和描述粗糙度各向异性的三维粗糙度参数系统,该系统克服了采样间隔的影响。Brown 等[13]利用雷诺方程和节理表面形态分形模型,研究了节理粗糙度对节理渗流特性的影响。也有学者通过建立粗糙度和JRC 与分形维数D之间的数值关系[14-15],解决了粗糙度和JRC 的量化问题。单一的分形维数无法真实反映裂隙面形态对单裂隙渗流特性的影响,结合数码成像、3D 扫描/打印等新技术开展裂隙渗流研究是一种新的趋势[16]。
天然的岩体裂隙面是粗糙、不规则的,若将平均隙宽或机械隙宽应用于立方定律,计算结果会存在较大的误差[17-21]。为了提高立方定律的适用性,Lomize[22]、Louis[23]、Barton 等[24]、速宝玉等[25]、Kishida 等[26]、Wang 等[27]基于试验及统计分析,提出了不同立方定律修正公式。周创兵等[28]根据立方定律求得渗透系数,结合试验与数值模拟成果,分析了粗糙裂隙的渗流规律。Belem 等[29]和Homand等[30]采用三维平均角度、参数Z2、表面相对粗糙度系数、表观各向异性程度和表面弯曲度系数等5个粗糙度参数来描述及表征三维节理表面几何信息。张鹏等[31]基于Belem 三维表面粗糙度表征理论,引入裂隙表面局部坡向概念,提出了一种能够反映裂隙剪切方向与裂隙表面各向异性关系的三维表面粗糙度表征方法。肖维民等[32]将节理平面离散成单元格,建立节理渗流空腔模型,研究粗糙裂隙的渗流特性。郭保华[33]研究了粗糙度系数、粗糙轮廓指数、粗糙角、分维和截距等参数的相互关系。Tang 等[34]提出了一种基于亮度面积百分比(BAP)表征岩石节理三维粗糙度的方法。王志良等[35]基于Boltzmann 格子方法,讨论裂隙面粗糙度对渗流流态的影响。申林方等[36]采用中点插值法以及Boltzmann 格子法,研究粗糙岩体裂隙几何形貌对裂隙渗流特性的影响。上述学者采用不同粗糙度表征参数来描述粗糙裂隙形貌对裂隙渗流特性的影响,也有学者侧重研究正应力、剪应力、裂隙接触面积等因素对裂隙渗流过程的影响[37-42]。自然界中岩体裂隙面多为上凸形态粗糙面,而以上研究成果多是基于上凸形态岩体粗糙面提出的。水工混凝土结构(隧洞衬砌、溢洪道、导墙、渠道等),一般是预制浇筑而成,其多孔混凝土粗糙面呈下凹分布特点,相对于同条件下的上凸形态粗糙面,其平均裂隙宽度大。上凸形态粗糙面凸起程度与裂隙过流能力是负相关的,而下凹形态粗糙裂隙面下凹程度与裂隙过流能力是正相关的,两种形态粗糙裂隙面对裂隙过流能力的影响不同。
本文基于下凹形态的粗糙裂隙面,利用数字成像技术采集粗糙裂隙面下凹数字信息,提出一种描述下凹形态裂隙面粗糙程度的新方法,结合MATLAB 随机函数拟定不同下凹度的粗糙面,建立下凹形态粗糙裂隙的立方定律修正公式。基于数值模拟和物理模型试验成果,验证立方定律修正系数公式和参数取值的合理性。
2 下凹度表征方法
上凸形态的裂隙面粗糙程度常采用起伏差[35]、节理粗糙系数JRC[13]和分数维D[43]来表征,本文引入裂隙面下凹度参数来表征下凹形态裂隙面粗糙度。采用高倍数数码相机(1000 万像素),对裂隙面进行数字成像,单次拍摄区域为500 mm×500 mm,每个试样拍摄3 次。结合软件统计处理的方法获取粗糙裂隙面信息并使其数值化,拍摄后未处理的某个裂隙面图片如图1(a)所示,将拍摄后图形文件导入Photoshop,生成具有黑、深灰、浅灰、白四种色阶的图像,如图1(b)所示。
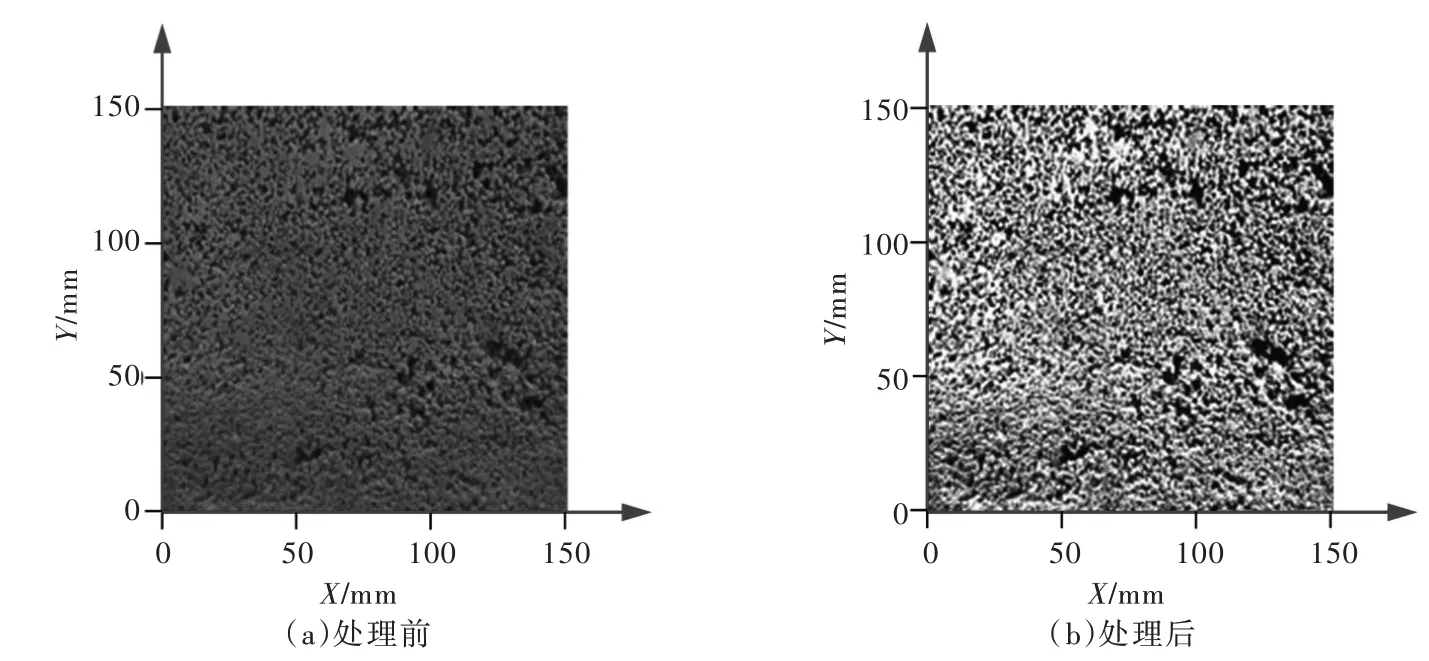
图1 裂隙面数字成像图
将图像与实际裂隙面相应位置进行探针测量,测量结果表明白色裂隙基准面的下凹度为0 ~0.15 mm,浅灰色、深灰色及黑色区域下凹度分别为0.15 ~0.45 mm、0.45 ~0.75 mm 及0.75 ~1 mm。采用Photo⁃shop 软件进行统计计算,四种不同色阶区域占整个裂隙面的面积百分比分别为51%、24%、17%和8%。将4 种不同(白、浅灰、深灰及黑)色阶的下凹程度分别按0.075 mm、0.300 mm、0.600 mm、0.875 mm 进行统计,即可得到3 组不同孔隙介质裂隙面下凹面积百分比随下凹度的变化规律,如图2所示。由于多孔混凝土(孔隙介质)浇注工艺以及Photoshop 数字化特点,使通过高像素数码相机成像的粗糙裂隙面图像具有以下特点:粗糙裂隙面表面整齐,局部下凹,而且不同下凹区域的下凹程度不同;3 个孔隙介质的裂隙基准面面积占50%左右,远高于下凹部分面积;随着下凹程度的加大,其所在区域逐渐减小。

图2 不同孔隙介质裂隙面各色阶面积占比随下凹度的变化规律
孔隙介质的孔隙分布比较均匀,其裂隙面下凹分布相对均匀。针对这一构造特点,利用MAT⁃LAB 软件进行处理,不同下凹程度区域在整个裂隙面分布相对均匀,其三维裂隙面的每个标准剖面的粗糙度取平均下凹度进行表征,沿裂隙水流流动方向随机生成该裂隙介质的裂隙结构面,数值化后的孔隙介质P-1 裂隙面示意图如图3所示。如图3所示,多孔混凝土的浇筑特点导致其裂隙面呈现表面整齐、局部下凹的粗糙形态,引入裂隙面下凹度φ来表征裂隙面的粗糙程度。
采用等效均质方法,选取各色阶区域面积占比与其平均下凹程度乘积之和来表征整个裂隙面下凹程度,如白色区域的面积百分占比为a(平均下凹0.075 mm),浅灰色区域面积百分占比为b(平均下凹0.300 mm),深灰色区域面积百分占比为c(平均下凹0.600 mm),黑色区域面积百分占比为d(平均下凹0.875 mm),则其裂隙面下凹度φ由下式计算:
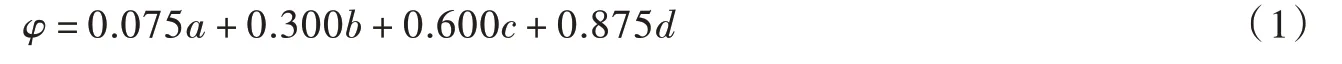
故该第一组孔隙介质P-1 的下凹度φ为0.282 mm,同理可得到另外两种孔隙介质裂隙面下凹度为0.300 mm 和0.324 mm。

图3 孔隙介质P-1 裂隙面示意(单位:mm)
3 试验论证
3.1 试验装置及材料裂隙渗流试验系统包含水循环控制系统、数据采集系统和试验模块[44],如图4所示。水循环控制系统确保供水循环使用,且控制上、下游水箱水头;数据采集系统采集试样内部水压、水温和流量等的实时数据。试验模块由一个长1200 mm、宽300 mm、高500 mm 的多孔混凝土砌块和相邻的长1700 mm、厚3.5 mm、高500 mm 的有机玻璃板组成。多孔混凝土块和有机玻璃板之间有间隙,间隙是通过插入不锈钢垫片形成的,在混凝土块和有机玻璃板之间形成厚度为1.0 mm 的间隙模拟裂隙,如图5(a)所示。采用的多孔混凝土配合比水泥∶水∶石英砂∶黄沙为2∶1∶9∶1,浇筑了三组多孔混凝土块,渗透系数分别为0.19、0.37 和0.88 cm/s。试验模块的进、出口流量控制开关布置如图5(b)所示。由直径为6.0 mm 高强度不锈钢管和HM-20-1-A1-F1-W2 水压传感器测量块体和裂缝内不同位置的水压。在浇筑多孔混凝土时,测压管被预埋在多孔混凝土中,各测试模块中埋管的分布如图6所示。进水和出水流量采用LDG15 集成电磁流量计测量,最大流量为99.0 m3/h,精度为0.001 m3/h。

图4 双重介质渗流系统装置

图5 渗流试验模块
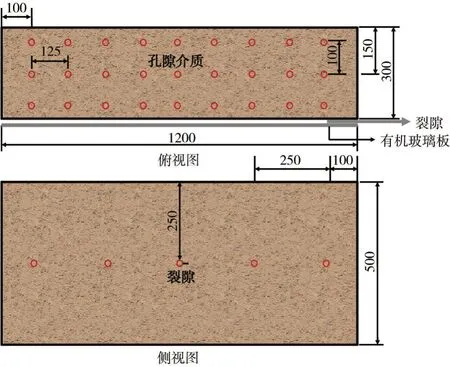
图6 试验模块水压测量位置布置图(单位:mm)
3.2 结果论证对三种孔隙介质随机裂隙面和光滑裂隙面进行数值模拟,计算得到上、下游水头1.0 m、隙宽1.0 mm、水温18 ℃时裂隙的流量,三组孔隙介质(P-1、P-2 和P-3)和光滑裂隙单宽流量分别为8.980×10-4、9.160×10-4、1.040×10-3和8.134×10-4m2/s。假定三组孔隙介质和光滑裂隙面的单宽出流量分别为q1、q2、q3和q,第i组孔隙介质在隙宽为1.0 mm 时的等效水力隙宽Bi计算公式如下:

式中:ξ为粗糙修正系数;B为光滑裂隙面隙宽;i为第i组孔隙介质。由式(3)可以计算三组孔隙介质裂隙面的水力隙宽分别为1.048、1.059 和1.127 mm。
上、下游水头1.0 m、隙宽1.00 mm、水温18 ℃时,两种不同进水方案下双重介质渗流模型试验结果、数值计算结果和考虑裂隙粗糙程度修正后的裂隙介质出水量占出水总量百分比如表1所示。由表1可知,光滑裂隙情况下的计算值与双重介质裂隙渗流试验结果的平均绝对误差MAE、均方根误差RMSE和平方根R2分别为8.86%、3.87×10-4和0.929;考虑裂隙面粗糙度,修正后的裂隙介质出水量占比计算值与试验值的平均绝对误差MAE、均方根误差RMSE和平方根R2分别为1.35%、1.06×10-4和0.995。修正裂隙面粗糙程度的计算值更接近试验值,说明采用数码成像,结合MATLAB 软件随机生成裂隙面的方法适用于研究下凹形态孔隙介质裂隙面粗糙度对裂隙过水能力的影响。

表1 试验值与计算值比较
4 立方定律修正
4.1 典型粗糙裂隙面根据孔隙介质粗糙裂隙面的构造特点,拟定如下13 个典型裂隙面,各裂隙面的四个色阶区域面积占比和下凹度值信息如表2所示。利用MATLAB 软件随机函数,结合CAD 软件生成13 个典型裂隙面,典型裂隙面形态如图7所示。

表2 典型裂隙面信息

图7 典型粗糙裂隙图
上、下游水头为1.00 m、水温18 ℃时,13 个典型粗糙裂隙面(F-1 ~F-13)与光滑裂隙面组成的裂隙的单宽流量Q与裂隙宽度之间的变化关系如图8所示。由图8可知,随着裂隙开度增大,裂隙单宽流量也随之增大,且增速不断变大;同裂隙宽度情况下,裂隙面下凹度越大,裂隙的单宽流量越大。裂隙单宽流量与裂隙开度和下凹度正相关。

图8 不同下凹度条件下裂隙单宽流量与裂隙开度变化曲线
4.2 立方定律修正函数
4.2.1 修正函数参数拟合 国内外许多学者对粗糙裂隙渗流特性做了研究,建立了单宽流量q与代表隙宽B(如水力隙宽Bh、平均隙宽、机械隙宽Bm等)的关系式,如Lomize[22]和Louis[45]将裂隙水流态严格划分为层流与紊流, 分别提出了层流情况下的岩体裂隙水流的计算公式:

式中:μ为流体动力黏滞系数;q为裂隙渗流量。
Barton[24]提出JRC(节理粗糙度系数)修正法,将等效水力隙宽Bh与机械隙宽Bm联系起来。在立方定律中建议裂隙宽度采用等效水力隙宽:

Iwai[46]考虑裂隙接触面积率的影响,提出下式:

式中:Q为相应于接触面积率ω的流量;Q0为ω=0 时的流量;ω为隙面面积接触率(裂隙面凸起接触面积与总面积之比);η为经验系数。
速宝玉[25]认为粗糙岩体裂隙隙宽一般均不大,多数为10-3~10-1mm,实际岩体裂隙水流多数处于层流、光滑紊流和过渡区,难于进入充分发展的紊流阶段。将层流近似看作为一种非线性程度极弱的流动,提出了一个紊流、层流统一的经验公式:

式中m为裂隙水流非线性指数。
归纳以上各式,可写为统一形式:

式中:α为粗糙裂隙流量的修正系数。针对孔隙-裂隙双重介质水力特性试验中孔隙介质裂隙面的构造特点,需要建立α、下凹度φ和裂隙宽度B的关联。
下凹度φ对立方定律的修正系数α的表达式为:

式中:q为不同下凹度情况下裂隙的单宽流量,m2/s;q0为相同隙宽条件下光滑裂隙的单宽流量,m2/s。
取0.25、0.50、0.75 和1.00 mm 四个不同隙宽的工况进行修正函数的参数拟合,修正系数α如表3所示。0.40 mm 隙宽各工况计算值用于拟合函数的检验。
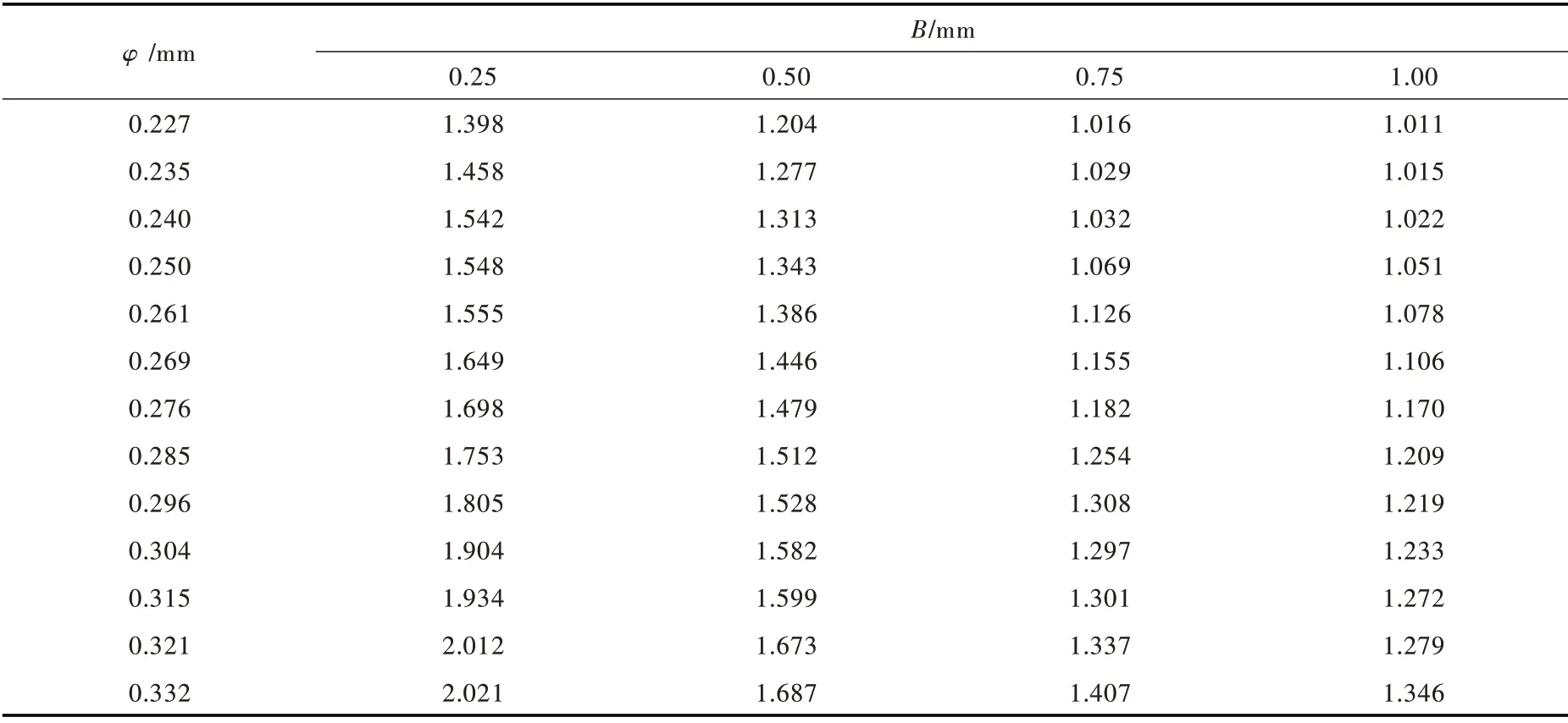
表3 不同工况修正参数α 值
为研究不同裂隙宽度B情况下下凹度φ对修正系数α的影响,引入相对下凹度φ′,构造立方定律修正函数α=f(φ′)。相对下凹度φ′与修正系数α的关系分析呈现较好的二次多项式关系。故采用二次多项表达式拟合不同裂隙宽度下相对下凹度φ′与修正系数α的关系,即:

式中:α为粗糙裂隙立方定律修正系数;a,b,c为经验常数。由于相对下凹度φ′=0 ,为光滑裂隙,修正系数α=1,故c=1.0。
根据图9中拟合得到a、b参数值,分别与裂隙宽度B进行拟合,拟合曲线如图10所示,拟合表达式为:



图9 相对下凹度-修正系数关系曲线

图10 裂隙宽度-拟合参数关系曲线
基于立方定律修正系数计算式(14),选取裂隙宽度B在0.02 mm ~0.30 mm 间的几组数据进行分析,其修正系数α与下凹度φ的关系曲线如图11所示。由图11可知,当裂隙宽度B一定时,裂隙面下凹度越大,其修正系数越大;随着B的增大,修正系数对下凹度敏感程度降低,裂隙宽度B大于0.10 mm,修正系数随裂隙面下凹度增大而增长速率减小,当裂隙宽度0.30 mm 时,裂隙面下凹度0.10 mm 对应的修正系数为1.029,而裂隙面下凹度0.40 mm 对应的修正系数为2.519。因此,对于涉水混凝土结构而言,可通过混凝土抗裂设计控制裂缝宽度,同时在预制养护过程中尽量减小裂隙面下凹度,减小混凝土裂缝渗漏量。实际岩体工程中, 除极少数较大断裂构造外, 绝大多数为细小裂隙[25],而露天高湿环境下混凝土裂缝最大允许宽度不超过0.30 mm,也是细小裂缝为主,一般宽度为10-3~10-1mm 量级,故本文提出立方定律修正系数计算公式具有较广泛的应用前景。
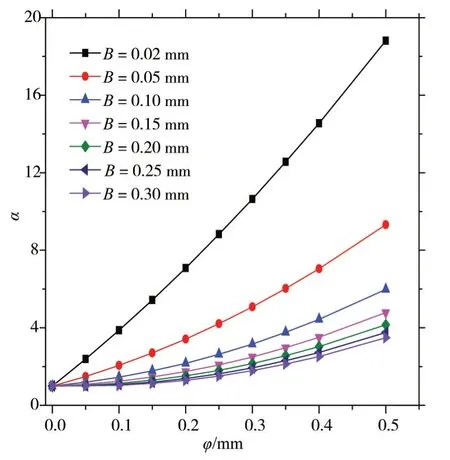
图11 裂隙面下凹度-修正系数关系曲线
4.2.2 修正函数验证 裂隙宽度0.40 mm 时各下凹度工况下的修正系数α用Comsol Multiphysic[47]软件进行数值模拟,将数值计算得到修正系数值与采用公式(14)计算得到的修正系数α进行比较,如图12所示。
由图12可知,裂隙宽度0.40 mm 时,两种方法得到的立方定律修正系数值平均绝对误差为1.75%,R2和RMSE分别为0.983 和0.023,说明拟定的修正系数公式和参数是合理的。同时,将采用该修正系数公式得到的裂隙过流单宽流量和试验测得的单宽流量值进行对比,选取裂隙宽度为1.0 mm,水温18 ℃,裂隙进水方式下三种不同孔隙介质(P-1、P-2 和P-3)工况进行分析,孔隙介质P-1、P-2 和P-3 对应的下凹度分别为0.282 mm、0.300 mm 和0.324 mm,采用公式(19)可以求得修正系数值分别为1.141、1.203 和1.295,根据立方定律计算光滑裂隙过流的单宽流量,再结合公式(15)即可求得三种孔隙介质裂隙面的单宽流量,其计算结果见表4。
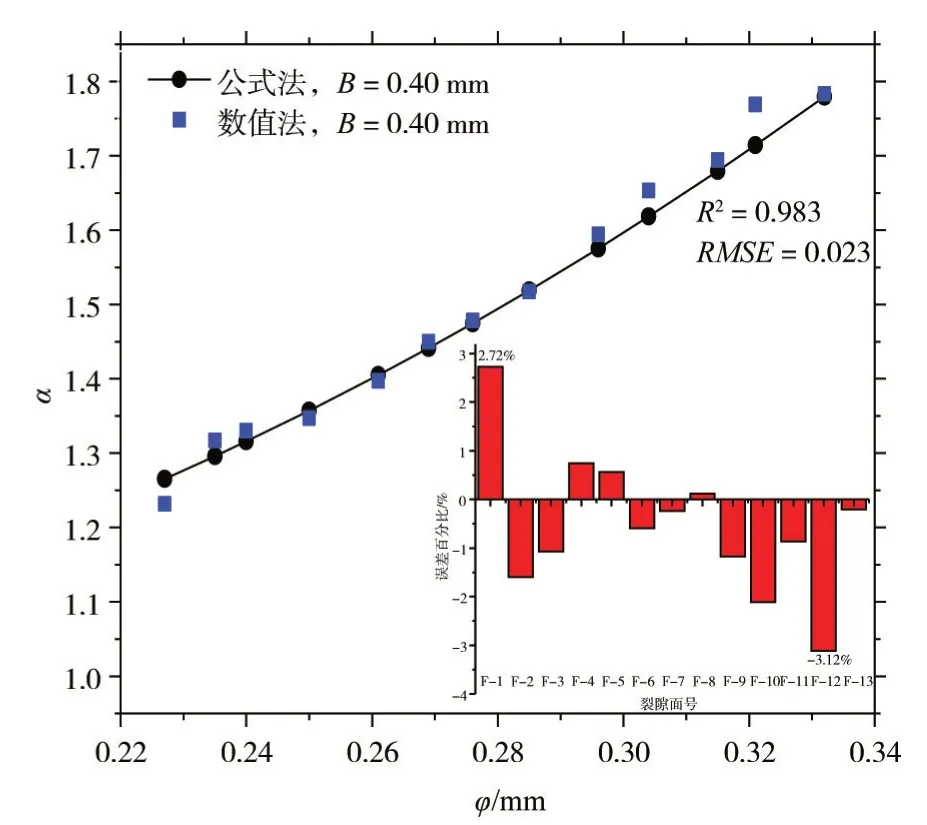
图12 不同下凹度下数值和公式方法得到的修正系数对比

表4 裂隙单宽流量试验值和计算值
由表4可得:随着裂隙面下凹度数值的增大,采用修正系数公式计算得到的单宽流量和试验测定的裂隙单宽流量均增大,符合一般规律;三种不同孔隙裂隙面情况下的裂隙单宽流量计算值和试验值最大相对误差为6.83%,平均绝对误差和RMSE分别为3.82%和4.080×10-4m2/s。
综上研究表明,基于高像素数码相机成像和MATLAB 技术,拟定下凹形态孔隙介质粗糙裂隙面,结合孔隙介质粗糙裂隙面相对下凹度,提出粗糙裂隙立方定量修正系数公式,该综合研究方法是合理可行的,适用于下凹形态粗糙裂隙面的裂隙渗流研究,研究成果可为涉水混凝土结构裂缝渗漏量估算提供理论依据。但本文拟合得到的修正系数公式和参数是基于下凹形态孔隙介质粗糙裂隙面和光滑裂隙面所构成的裂隙,并不适用于所有形态粗糙裂隙,且未考虑正应力、剪应力、接触面积及裂隙弯曲度对裂隙渗流的影响,存在一定局限性。
5 结论
本文针对下凹形态的粗糙裂隙面,引入下凹度参数来表征裂隙面的粗糙程度,结合裂隙开度对立方定律公式进行修正,提出修正系数计算公式,具体结论如下:
(1)使用高像素照相机采集孔隙介质模块粗糙裂隙面的信息,结合MATLAB 软件对裂隙面信息进行数学处理,按下凹程度0.075、0.300、0.600 和0.875 mm 对粗糙裂隙面信息进行统计,得到孔隙介质试验模块的各色阶区域面积占比随下凹程度的变化规律。
(2)提出用下凹度来描述下凹形态孔隙介质裂隙面粗糙度的方法。按裂隙面下凹度随机生成三组孔隙介质粗糙裂隙面,上、下游水头为1.00 m、隙宽1.0 mm、水温18 ℃时,修正后的裂隙介质出水量占比计算值与试验值的MAE、RMSE和R2分别为1.35%、1.06 × 10-4和0.995,与试验值更为吻合,说明该方法适用于研究下凹形态孔隙介质裂隙面粗糙程度对裂隙渗流特性的影响。
(3)基于孔隙介质试验模块各色阶区域面积百分占比随下凹度变化规律,随机生成13 个典型粗糙裂隙面,引入相对下凹度,拟定立方定律修正函数公式,并拟合公式参数。当裂隙宽度0.40 mm 时,数值和修正公式计算得到的立方定律修正系数值平均绝对误差为1.75%,R2和RMSE分别为0.983 和0.023;裂隙宽度为1.00 mm 时,孔隙介质P-1、P-2 和P-3 对应修正系数值分别为1.141、1.203 和1.295,裂隙单宽流量计算值和试验值最大相对误差为6.83%,MAE和RMSE分别为3.82%和4.080 ×10-4m2/s。综上说明本文所提出的粗糙程度表征方法和立方定律修正公式是合理的,适用于下凹形态粗糙裂隙渗漏量估算,具有应用前景。

