铜胁迫下玉米叶片光谱STFT分析与叶片铜离子浓度反演

孟 飞 崔 宇 付萍杰

(山东建筑大学测绘地理信息学院， 济南 250101)

0 引言

土壤重金属污染是影响农作物正常生长的重要因素之一，其中铜(Cu)、铅(Pb)、镉(Cd)等重金属污染较为突出[1]。土壤重金属污染隐蔽性强、毒性大、治理难且周期长[2]。以Cu为例，常量时Cu是植物生长发育的必需微量元素[3]，而土壤Cu2+含量的超标会破坏农作物细胞组织结构，引起植物代谢紊乱[4]。受重金属胁迫的农作物不但生长会受到抑制，而且土壤生理化参数也会发生改变[5]，这些变化都会反映在光谱曲线上。因此，利用光谱技术对农作物重金属污染胁迫等弱信息进行提取与判别已成为高光谱遥感的研究热点，快速有效地监测农作物重金属污染对生态系统的安全与稳定具有重要意义。研究利用叶片光谱判别玉米铜胁迫程度的最佳生长阶段同样具有重要意义[6]。

高光谱数据具有波段众多、光谱分辨率高的优势，可实现农作物快速、无损、实时的动态监测[7-8]，也为监测和防治土壤总金属污染提供了技术保障[9]。刘厚田等[10]基于一、二阶微分分析了土壤中过量铜对水稻叶片光谱反射特性的影响；李苑溪等[11]研究发现，铜胁迫下玉米叶片光谱红边波长与叶片中叶绿素含量存在一定的相关关系；高鹏等[12]基于铜胁迫下玉米叶片光谱的MRSVD特征构建奇异特征参数，进行了光谱奇异性分析，并采用逐步回归分析法建立奇异特征参数与玉米叶片Cu2+含量之间的定量关系模型。光谱时频分析在前人研究中同样有了长足的发展。杨可明等[13]采用结合EMD算法的HHT时频分析方法，对不同浓度Cu2+污染下土壤光谱进行信息挖掘及诊断，并依据信息进行Cu2+浓度的反演；姜雪芹等[14]将谐波分析与BP神经网络结合，利用土壤高光谱遥感的传统处理数据进行土壤含水率反演，取得较好的效果；李旭青等[15]基于小波变换和BP神经网络建立水稻冠层重金属含量反演模型，该模型精度较高，具有一定的实用性。信号的STFT时频分析方法是针对非平稳信号非常有效的分析工具[16-17]。晁娇[18]对不同类型复杂雷达信号经STFT变换后的结果进行统计，形成了基于短时傅里叶变换的雷达信号脉内特征自动识别流程，这对电子侦察情报的获取及应用具有重要意义；同晓荣[19]提出一种基于STFT的声信号盲分选算法，优化了声信号盲分选仿真系统的实时性，提高了分选精度；张博等[20]基于轨道高低不平顺数据提出一种基于STFT时频分析模型的高速铁路路基局部变形识别方法；LIU等[21]提出了一种基于STFT的端点检测方法，应用于光纤干涉振动传感系统；NARASIMHAN等[22]提出一种新的STFT控制算法，以减少基础隔震建筑物的响应；CHIKKERUR等[23]提出了一种基于STFT分析的指纹增强新方法，提高了传统指纹识别精度。尽管高光谱遥感已广泛应用于农业检测领域，但传统的农作物重金属污染监测多数围绕植被原始光谱获取较为复杂的光谱特征参数，而重金属胁迫下农作物叶片光谱信号产生的变化微小，根据传统监测方法和常规的光谱特征参数很难区别光谱之间的微弱差异[24]，因此引入在雷达信号、声音信号、光线信号、电信号等异常检测中广泛应用的STFT时频分析方法，研究重金属胁迫下农作物叶片光谱响应。

传统的STFT对较为平滑的信号反应并不敏感，本文结合一阶微分和STFT方法的优势，对农作物原始平滑光谱做一阶微分处理后进行STFT时频分析，研究重金属胁迫下的农作物叶片光谱信号能量随波长和频率聚集形态的众多参数，通过分析揭示重金属胁迫下农作物叶片光谱的时频能量变化规律，同时依据其峰值能量参数建立玉米叶片Cu2+浓度反演的多变量偏最小二乘回归模型，以期实现基于光谱时频分析法的农作物重金属胁迫的快速、简单、有效监测。

1 实验设计与数据采集

1.1 实验设计

选用含有Cu2+的CuSO4·5H2O溶液作为重金属胁迫源，植物样品选用“中糯1号”玉米进行培养，实验分别设置0、50、200、300、400、800、1 200 μg/g 7个浓度梯度，分别标记为CK、Cu(50)、Cu(200)、Cu(300)、Cu(400)、Cu(800)和Cu(1200)，其中CK(0 μg/g设计浓度的植物样品)为对照组，未添加CuSO4·5H2O，每个浓度梯度设置3组同期培养的平行实验，组1为实验组，组2、3为验证组，共计21盆盆栽，作为研究用培养植物，用于获取玉米叶片光谱。

1.2 玉米叶片光谱采集

采用美国SVC公司生产的SVC HR-1024I型高性能地物光谱仪测定Cu2+胁迫下玉米叶片光谱。光谱采集使用功率为50 W的卤素灯光源和4°视场角探头，探头垂直于叶片表面40 cm，每盆玉米叶片光谱测量3次，由原始扫描光谱自动平均得到输出结果，光谱反射系数经专用平面白板标准化处理，由此得到不同Cu2+浓度胁迫下的玉米叶片光谱。不同浓度梯度Cu2+胁迫下玉米叶片光谱如图1所示。

1.3 叶片Cu2+浓度测定

对采集的玉米叶片样品经过冲洗、干燥、粉碎等预处理后封装在样品袋中，样品经高纯硝酸、高氯酸消化后，用WFX-120型原子吸收分光光度计测定Cu2+浓度。各浓度梯度Cu2+污染胁迫下3组玉米叶片样本中Cu2+浓度见表1。

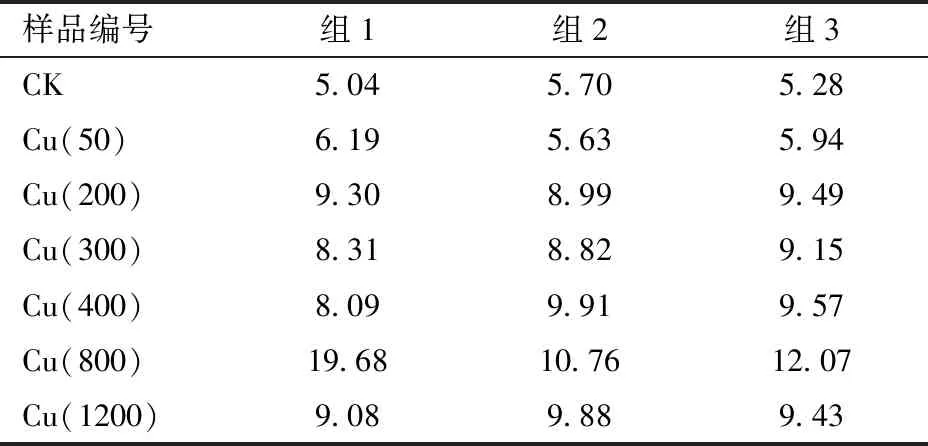
表1 不同浓度梯度Cu2+胁迫下玉米叶片Cu2+实测浓度Tab.1 Measured concentration of Cu2+ in maize leaves under different concentrations gradient Cu2+ stress μg/g

2 研究方法

2.1 光谱信号处理

2.1.1光谱一阶微分

光谱信号的预处理包括归一化、一阶微分、统去除等，其中对光谱的一阶微分处理是最为常用的方法。光谱数据进行一阶微分处理可以去除线性或接近线性的背景噪声对目标光谱的影响[25],也能提供比原光谱更高分辨率和更清晰的光谱轮廓变换[26]，且相比原始平滑光谱曲线，光谱一阶微分曲线更加不平稳，进一步有利于信号的STFT变换处理。光谱一阶微分计算式为

SD(λi)=(ρ(λi+1)-ρ(λi-1))/Δλ

(1)

式中λi——光谱波长

ρ(λi+1)、ρ(λi-1)——光谱反射率

SD(λi)——光谱一阶微分

Δλ——波长λi+1与λi-1的波段间隔

2.1.2光谱短时傅里叶变换(STFT)

STFT变换的基本原理是把原始信号和窗函数进行相乘并进行一维的傅里叶变换，然后通过窗函数的滑动得到一系列频谱函数，将频谱函数随时域依次展开可得到该信号的三维时频图，即信号随时间和频率变化的复数幅度。STFT变换的时间分辨率和频率分辨率之间不能兼得，窗长越长，频率分辨率越高，时间分辨率越差[27]。STFT常用窗函数有Hamming窗、Hanning窗、矩形窗、高斯窗等。STFT变换公式为

(2)

式中Z(u)——u时刻的原信号

g(u-t)——窗函数f——角频率

2.2 回归模型

2.2.1多元线性回归

多元线性回归模型(MLR)通常用于研究一个因变量与多个自变量的变化关系，若二者的关系可以用线性形式来描述，则可以建立多元线性模型进行分析。本文分别以7组受不同浓度Cu2+胁迫下叶片光谱一阶微分参数及光谱一阶微分STFT分析参数为因变量，实测叶片Cu2+浓度为自变量，在SPSS中建立叶片Cu2+浓度反演的多元线性回归模型。由于光谱一阶微分及光谱一阶微分STFT分析参数较多，SPSS软件自动剔除对因变量无显著影响的自变量，保留6个对因变量有显著影响参数，分别建立六变量多元线性回归模型，反演叶片Cu2+浓度。MLR模型为

y=β0+β1x1+…+β6x6

(3)

式中x1、x2、…、x6——非随机变量，叶片光谱一阶微分参数及光谱一阶微分STFT能量幅值

y——因变量，模型预测Cu2+浓度

β0、β1、…、β6——回归系数

2.2.2偏最小二乘回归

偏最小二乘回归(PLSR)是一种统计学方法，与主成分回归有关，利用多因变量对多自变量进行回归建模。PLSR模型通过投影分别将频谱和相关响应变量投影到一个二维空间，来寻找一个线性回归模型，从而降低维数并避免噪声[28]。相比传统回归分析，在自变量多、样本数量较少的情况下，PLSR有更明显的优势[29]。本文分别以7组受不同浓度Cu2+胁迫下叶片光谱一阶微分参数及光谱STFT时域特征波段上随频域变化的STFT时频能量幅值(每个特征波段包含65个幅值)为因变量，以实测叶片Cu2+浓度为自变量分别建立多变量PLSR模型，反演叶片Cu2+浓度。PLSR模型流程图如图2所示(以STFT能量参数为例)。

2.3 模型精度验证

采用决定系数R2评价模型预测值与实测值的拟合精度。决定系数R2是回归平方和占总误差平方和的比例，反映回归直线的拟合程度，其取值范围介于0～1之间。R2越趋近于1，说明回归方程拟合精度越高；R2越趋近于0，说明回归方程拟合精度越差。同时采用均方根误差RMSE评价模型精度，反映模型预测值与实测值之间的离散程度，RMSE越小，说明模型预测值与实测值之间离散程度越小，模型精度越高。

3 结果与分析

3.1 光谱一阶微分分析

用式(1)对获取的波段340～1 000 nm玉米叶片光谱信号进行一阶微分处理，发现不同浓度Cu2+胁迫下玉米叶片光谱一阶微分处理后在波段480～670 nm、700～750 nm处产生较为明显的峰值及低谷变化，原因是该波段范围是较易受重金属胁迫影响的玉米叶片光谱响应特征的“紫谷-绿峰-红谷”所对应的波段范围[30]。通过信号的STFT变换，能够在该明显“峰值-低谷”变化范围获取其对应时频能量的变化规律，并针对相应规律及参数做进一步研究。不同浓度梯度Cu2+胁迫下玉米叶片光谱一阶微分处理结果如图3所示。

3.2 光谱的STFT分析

以不同浓度梯度Cu2+胁迫下波段340～1 000 nm玉米叶片光谱的一阶微分数据为原始信号，为突出光谱一阶微分STFT时频能量在一阶微分光谱“峰值-低谷”位置的能量值及其变化情况，设置采样间隔为1，FFT长度为128，窗口长度为32，采样重叠度为31，窗口选用Hamming窗进行STFT变换，获取不同浓度梯度Cu2+胁迫下波段340～1 000 nm玉米叶片光谱响应的一阶微分处理数据的时频图，将时域转换为虚拟光谱，如图4所示。能量振幅峰值所处波段随Cu2+浓度梯度变化情况见表2。

由图4可看出，随着Cu2+浓度的不断增加，能量振幅峰值呈先降低后升高趋势。结合表2，无重金属Cu2+胁迫的正常植株的光谱一阶微分STFT峰值所处波长为722 nm附近。随着Cu2+浓度不断升高，实验组与验证组的光谱一阶微分STFT时频能量峰值均在样品Cu2+浓度设置为400 μg/g时为最小值，峰值能量所处波段均出现在690～730 nm之间，且沿波段轴向左，即短波方向迁移，仅验证组组2与组3在Cu2+浓度800 μg/g与1 200 μg/g时振幅与所处波段出现极小反常情况，但未影响整体规律。红边(REP)是绿色植物叶子光谱曲线在波段680～740 nm之间变化率最快的点，也是一阶导数光谱在该区间内的拐点[31]，而重金属Cu胁迫程度增加会造成农作物红边“蓝移”程度增强[32]，因此玉米叶片光谱受重金属胁迫影响而产生的红边“蓝移”是其STFT时频峰值能量迁移的重要原因。

3.3 玉米叶片重金属Cu2+浓度反演

3.3.1基于光谱一阶微分变量的MLR及PLSR模型反演

选取17组不同Cu2+浓度梯度胁迫下玉米叶片光谱一阶微分处理参数为自变量，叶片实测Cu2+浓度为因变量，在SPSS软件中做多元回归线性拟合，建立Cu2+浓度反演的MLR模型。光谱一阶微分前共661个波段，一阶微分后得659个参数，将参数编号为Fod1、Fod2、…、Fod659，软件模型参数选取及对应系数如表3所示，模型R2=0.98(P<0.01)。

分别选取组2与组3光谱一阶微分参数对应参数代入模型进行Cu2+浓度反演，Cu2+浓度反演值与实测值对比见图5。由图5可得，光谱一阶微分参数建立的线性预测模型精度低，组2实测值与预测值R2=0.114，RMSE为5.696 μg/g；组3R2=0.120 1，RMSE为4.159 μg/g，且组2反演结果存在一个负值，表明简单的光谱一阶微分参数建立的六变量参数MLR模型尽管本身精度较高，但存在一定的局限，不能实现对验证组玉米叶片Cu2+浓度的准确预测。

选取17组不同Cu2+浓度梯度胁迫下玉米叶片光谱一阶微分全部参数为自变量，实测Cu2+浓度为因变量，在Matlab中建立一阶微分参数PLSR Cu2+浓度反演模型。模型自变量系数见图6a，精度验证见图6b，模型精度R2=1(P<0.01)，由于模型本身精度过高，存在过拟合现象，因此仅将此模型用于对比，而不能对其进行参考。

表3 一阶微分参数反演MLR模型选取编号及对应系数Tab.3 First-order differential parameter inversion MLR model selection number and corresponding coefficient

依据组1光谱一阶微分参数建立的PLSR模型，对组2与组3光谱一阶微分参数进行Cu2+浓度反演，模型反演值与实测值拟合见图7。由图7可见，组2与组3反演精度R2分别为0.619 2(P<0.05)和0.451 2，RMSE分别为6.05、5.429 μg/g，尽管模型对验证组反演精度有所提高，但总体离散程度较大，因此光谱一阶微分STFT参数建立的PLSR模型虽发挥了自变量多的优势，且模型本身精度极高，但其反演结果仅能用作对比，而不予对其参考。

3.3.2基于光谱一阶微分STFT参数的MLR及PLSR模型反演

同样选取17组不同Cu2+浓度梯度胁迫下玉米叶片光谱一阶微分STFT能量峰值所在时域波段上的能量参数为自变量，实测叶片Cu2+浓度为因变量，在SPSS软件中做多元回归线性拟合，建立Cu2+浓度反演模型。光谱一阶微分STFT处理后在频域上得65个参数，将参数编号为St1、St2、…、St65，软件模型参数选取及对应系数见表4，模型精度R2=0.97(P<0.01)，精度较高。忽略组2、3真实峰值所处波段，仍以组1建模波段为参数选取波段，将组2与组3光谱一阶微分STFT数据对应参数代入模型进行叶片Cu2+浓度反演，叶片Cu2+浓度模型反演值与实测值对比见图8。由图8可得，光谱一阶微分STFT参数建立的MLR预测模型组2实测值与预测值R2为0.509 5，RMSE为6.152 μg/g，组3R2为0.275 1，RMSE为4.921 μg/g，与光谱一阶微分参数建立的MLR模型相比，精度略有提高，但组3反演效果仍不理想，仅不存在负值反演结果。

为进一步提高STFT参数模型反演精度，发挥PLSR模型的优势，选取组1 Cu2+浓度梯度胁迫下玉米叶片一阶微分处理光谱的STFT变换虚拟光谱波段上特定波长随频域变化的65个全部能量幅值用作7组自变量，7个实测叶片Cu2+浓度用作因变量，在Matlab中建立PLSR Cu2+浓度预测模型。建立的PLSR线性回归模型自变量系数见图9a，模型精度验证见图9b。忽略验证组实际振幅峰值波段，仍以实验组建模参数波段为特征波段，依次选取组2与组3光谱响应一阶微分数据的STFT变换结果的对应波段全部能量幅值作为验证参数，代入PLSR模型进行叶片Cu2+浓度含量反演，并将反演结果与验证组实测Cu2+浓度进行线性拟合，拟合结果如图10所示。组2与组3R2分别为0.880 6与0.733 1(P<0.01)，RMSE分别为1.563、2.619 μg/g，相比SPSS软件建立的6自变量MLR模型，STFT参数的PLSR多自变量模型反演精度进一步提高，且反演结果离散程度较其他参数和模型的反演结果，有了大幅降低。

表4 一阶微分STFT参数反演线性模型选取编号及对应系数Tab.4 First-order differential STFT parameter inversion linear model selection number and corresponding coefficient

4 结论

(1)随着Cu2+胁迫浓度升高，受农作物“红边蓝移”现象的影响，光谱一阶微分STFT能量峰值参数呈先降低、后升高趋势，且峰值参数频谱随Cu2+浓度升高沿波段轴不断向短波方向迁移。峰值参数频谱的迁移状况与峰值参数可以作为判别玉米叶片光谱重金属胁迫程度的标志。

(2)相比一阶微分参数、一阶微分STFT分析参数的6自变量MLR模型，以及一阶微分参数PLSR模型，以峰值参数频谱的全部能量幅值为自变量、以实测玉米叶片Cu2+浓度为因变量建立的多自变量光谱一阶微分STFT参数的PLSR模型Cu2+浓度预测精度最高，且在对验证组两组参数进行反演时，预测值与实测值R2分别为0.880 6和0.733 1(P<0.01)，RMSE分别为1.563、2.619 μg/g。由此可见，若验证样本组数量足够多，且本文建立的模型能够利用相同方式获取参数对玉米叶片Cu2+浓度进行准确预测，则表明本文通过光谱STFT时频分析方法获取参数建立的Cu2+浓度预测模型存在一定的普适性。