气动肌肉力-位移迟滞特性实验与建模

孟德远 李顺利 杨 林 李艾民 唐超权

(1.中国矿业大学机电工程学院, 徐州 221116； 2.重庆大学机械工程学院, 重庆 400044)

0 引言

气动肌肉(PAM)是一种仿人体肌肉提供收缩力的气动执行元件。常见的McKibben型气动肌肉由橡胶管气囊、纤维编织网及两端固定装配件组成。由于编织网的纤维不可伸展，当气动肌肉充入压缩空气、气囊膨胀时，编织网纤维间的角度变化使气动肌肉缩短，从而产生轴向收缩力。气动肌肉具有功率-质量比大、柔顺性好、清洁、安装使用方便等优点，在仿生机器人[1-4]和农业机器人[5]领域具有广泛的应用前景，特别是在有清洁和大驱动力要求的农业采摘及处理场合。由于内部摩擦、橡胶管弹性变形等原因，气动肌肉具有非常复杂的输出特性，且收缩力与位移之间存在明显的迟滞现象[6-8]，精确控制气动肌肉的收缩量或长度十分困难。近年来，科研人员建立了许多气动肌肉力学模型，并用于控制器设计，显著改善了控制性能，但对气动肌肉的迟滞特性研究不够深入，导致难以进一步提高气动肌肉的控制精度，严重制约了该类执行器在上述领域的大规模应用。

物理系统的迟滞现象一直是研究热点，国内外学者提出了许多迟滞模型，其中以Prandtl-Ishlinskii模型[9-14](简称PI模型)、Maxwell-slip模型[15](简称MS模型)为代表的积分类模型和以Bouc-Wen模型[16-19](简称BW模型)为代表的微分类模型最常见。针对气动肌肉的迟滞特性，MINH等[15]忽略气动肌肉力-位移迟滞现象的非对称性，采用MS模型对其进行描述，并通过分析迟滞曲线变化趋势得到模型参数计算方法；LIN等[20]采用PI模型描述气动肌肉的位移-压力迟滞现象，并利用遗传算法进行模型参数辨识；王斌锐等[21]通过对PI模型的play算子进行修正来描述非对称迟滞现象，提出一种气动肌肉压力-位移迟滞的PI+Polynomial模型；XIE等[22]为更精确描述气动肌肉的位移-压力非对称迟滞现象，将PI模型与死区算子模型串联建立一种PI+Dead-zone模型，并利用最小二乘法进行模型参数辨识；王琦珑等[23]建立气动肌肉力-位移迟滞的改进BW模型，该模型的参数比积分类模型少，能描述具有非对称极点的迟滞曲线；ASCHEMANM等[24]建立气动肌肉力-位移迟滞的PI模型、MS模型和J-Song模型(一种通用BW模型)，并进行各模型参数辨识，通过实验对比发现，3种模型精度相差不大。需要指出的是，PI类模型具有的率不相关性与气动肌肉力-位移迟滞现象的特性相吻合，且其迟滞算子形状与气动肌肉的力-位移迟滞曲线相接近，因此，采用PI类迟滞模型来描述气动肌肉力-位移迟滞现象具有显著优势。由于气动肌肉力-位移迟滞现象的强非对称性，使其非对称信息无法由经典PI模型表达，加之存在其迟滞曲线与常用PI类迟滞模型方向不匹配的问题，导致建立一种适用于描述气动肌肉非对称力-位移迟滞现象的高精度PI类模型十分困难。

本文搭建气动肌肉收缩力测试实验台，通过实验得到气动肌肉力-位移迟滞曲线，分析并验证气动肌肉的力-位移迟滞的非对称性、非局部记忆性、大压力弱相关性和准率不相关性，基于PI+Dead-zone模型，并对其进行修正，建立一种高精度气动肌肉通用PI迟滞模型，并完成参数辨识，对模型精度进行分析，并与PI类模型及BW类模型等5种模型进行对比。

1 气动肌肉力-位移迟滞特性

通常将运动过程中气动肌肉的收缩力FM(ξ,p)分为静态力Fs(ξ,p)和迟滞力Fh(ξ,p)两部分，即

FM(ξ,p)=Fs(ξ,p)+Fh(ξ,p)

(1)

其中ξ=(lmax-l)/lmax×100%

式中p——气动肌肉腔内绝对压力

ξ——气动肌肉收缩率

lmax——气动肌肉原始长度

l——气动肌肉收缩后长度

图1展示了气动肌肉静态力与位移关系，将静态力从收缩力中减去，得到如图2所示的迟滞力与位移关系曲线，该曲线通常也被称为气动肌肉力-位移迟滞曲线。气动肌肉的力-位移迟滞现象呈现如下特性：

(1)非对称性

气动肌肉的力-位移迟滞曲线是非对称环形曲线，即气动肌肉收缩和恢复原始长度过程中的迟滞力关于中心(位移与迟滞力中点)不对称。

(2)非局部记忆性

如图3所示，保持气动肌肉腔内压力恒定、初始长度不变，不同行程下气动肌肉力-位移迟滞曲线的形状与位置存在显著差异。由此可见，气动肌肉的力-位移迟滞现象具有非局部记忆特性，即气动肌肉的迟滞力不仅与其当前长度有关，还受运动轨迹幅值、起始长度的影响。此外，行程越大，气动肌肉力-位移迟滞曲线的非对称性越显著，由此可见，非局部记忆性对气动肌肉力-位移建模及相关控制起着至关重要的作用。因此，对气动肌肉力-位移迟滞现象高精度建模需考虑不同行程的情况。

(3)大压力弱相关性

保持气动肌肉行程不变、起始长度不变，改变其腔内压力，测得气动肌肉的力-位移迟滞曲线如图4所示，当气动肌肉腔内压力大于一定值后，各力-位移迟滞曲线基本一致。由此证明气动肌肉在大压力、同行程、同起始长度条件下，其迟滞力受腔内压力影响较小。合理利用此特性可以简化气动肌肉迟滞建模的实验量。实验发现，对于本次实验被测型号气动肌肉，当实际工作中其腔内压力大于0.5 MPa，可认为其迟滞力与腔内压力无关。

(4)准率不相关性

保持气动肌肉运动行程和压力不变，改变其收缩速度和换向频率，测得气动肌肉力-位移迟滞曲线如图5所示，各迟滞曲线的形状及位置基本一致，表明收缩速度和换向频率对气动肌肉迟滞特性影响很小。保持气动肌肉运动行程和压力不变，改变气动肌肉运动轨迹类型，测得气动肌肉力-位移迟滞曲线如图6所示，两迟滞曲线也基本一致。由于实验时气动肌肉的换向误差较大，气动肌肉在运动两拐点附近迟滞曲线误差较大，但其迟滞曲线趋势一致。由此可得，气动肌肉力位移迟滞现象宏观上具有准率不相关性，即迟滞曲线形状与收缩速率及换向频率无关。

2 气动肌肉力-位移迟滞模型

以收缩率作横坐标时，气动肌肉力-位移迟滞曲线如图7所示，得到的迟滞力随收缩率增大而减小，且迟滞曲线呈逆时针方向。以长度作横坐标时，气动肌肉力-位移迟滞曲线如图8所示，得到的迟滞力随肌肉长度增大而增大，且迟滞曲线呈顺时针方向。本文选定以气动肌肉长度作为横坐标绘制力-位移迟滞曲线。

2.1 经典PI模型

气动肌肉力-位移迟滞现象的经典PI模型[20]描述为

(2)

式中FPI(k)——k时刻经典PI模型输出

wi——第i个stop算子的权重

yi(k)——第i个stop算子的输出

为使经典PI模型与气动肌肉力-位移迟滞曲线的方向相匹配，常用的play算子[20](图9a)其方向呈由小到大逆时针方向，与图8所示迟滞曲线的方向并不一致。选用如图9b所示的stop算子[25]作为基本算子，此算子与图8所示迟滞曲线的方向均为由小到大顺时针方向，具体描述为

yi(k)=Hri[x,ri](k)= min(ri,max(-ri,x(k)-x(k-1)+yi(k-1)))

(3)

式中ri——第i个stop算子的阈值

x(k)——k时刻气动肌肉长度

Hri[x,ri](k)——第i个stop算子的输出

stop算子初始条件为

yi(0)=min(ri,max(-ri,yi0))

(4)

在参数辨识过程中提前给定阈值为

(5)

式中Fh(k)——k时刻气动肌肉迟滞力测量值

实际应用中气动肌肉力-位移迟滞现象经典PI的模型描述为

FPI(k)=wTHr[x,y0](k)

(6)

其中w=(w1,w2,…,wn)T

Hr[x,y0](k)=(y1(k),y2(k)，…,yn(k))Ty0=(y0r1,y0r2,…，y0rn)T

式中w——stop算子权重向量

Hr[x,y0](k)——stop算子k时刻输出向量

y0——stop算子初始状态向量

通过stop算子加权叠加方式，气动肌肉经典PI模型继承了其映射特性，将k时刻模型输出迟滞力与模型输入气动肌肉长度对应。式(3)中stop算子在某确定时刻的输出与速度、频率等无关，且是由上一时刻递推得到，加权叠加后并未改变这些特性，因此经典PI模型具有率不相关性。

2.2 修正PI+Dead-zone模型

原PI+Dead-zone模型[9]采用play算子与dead-zone算子相级联，可用于描述压电材料的非对称迟滞现象。于2.1节建立的气动肌肉经典PI模型中采用stop算子代替play算子解决了经典PI模型与迟滞曲线方向不匹配的问题，其原因为stop算子与迟滞曲线方向一致。由于在PI+Dead-zone模型中更换了PI模型的基本算子类型，此时若继续使用dead-zone算子会造成两类算子权重辨识失败。鉴于stop算子与play算子为互逆算子，其在方向上也互逆。据此，可从找到dead-zone逆模型角度出发，找到能替代dead-zone算子的“逆算子”并与stop算子相级联，以此建立适用于气动肌肉力-位移迟滞现象的修正PI+Dead-zone模型。dead-zone算子如图10a所示，其数学上的逆如图10b所示，采用此模型会造成在输入为0时，其输出值在纵坐标轴上滑动，此时模型明显会失效。因此，对其进一步做修正，得到图10c所示的修正dead-zone算子。

气动肌肉修正PI+Dead-zone模型描述为

(7)

Sd[FPI](k)=(q1(k),q2(k),…,qm(k))Twd=(wd1,wd2,…,wdm)T

式中FPI+Dead-zone(k)——k时刻修正PI+Dead-zone模型输出

Sd[FPI](k)——k时刻修正dead-zone算子输出向量

wd——修正dead-zone算子权重向量

wdj——第j个修正dead-zone算子权重

如图10c所示，第j个修正dead-zone算子qj(t)描述为

(8)

式中dj——第j个修正dead-zone算子阈值

在参数辨识过程中提前给定stop算子阈值及修正dead-zone算子阈值，stop算子阈值选取方式与经典PI模型相同，修正dead-zone算子阈值选取为

-∞<…

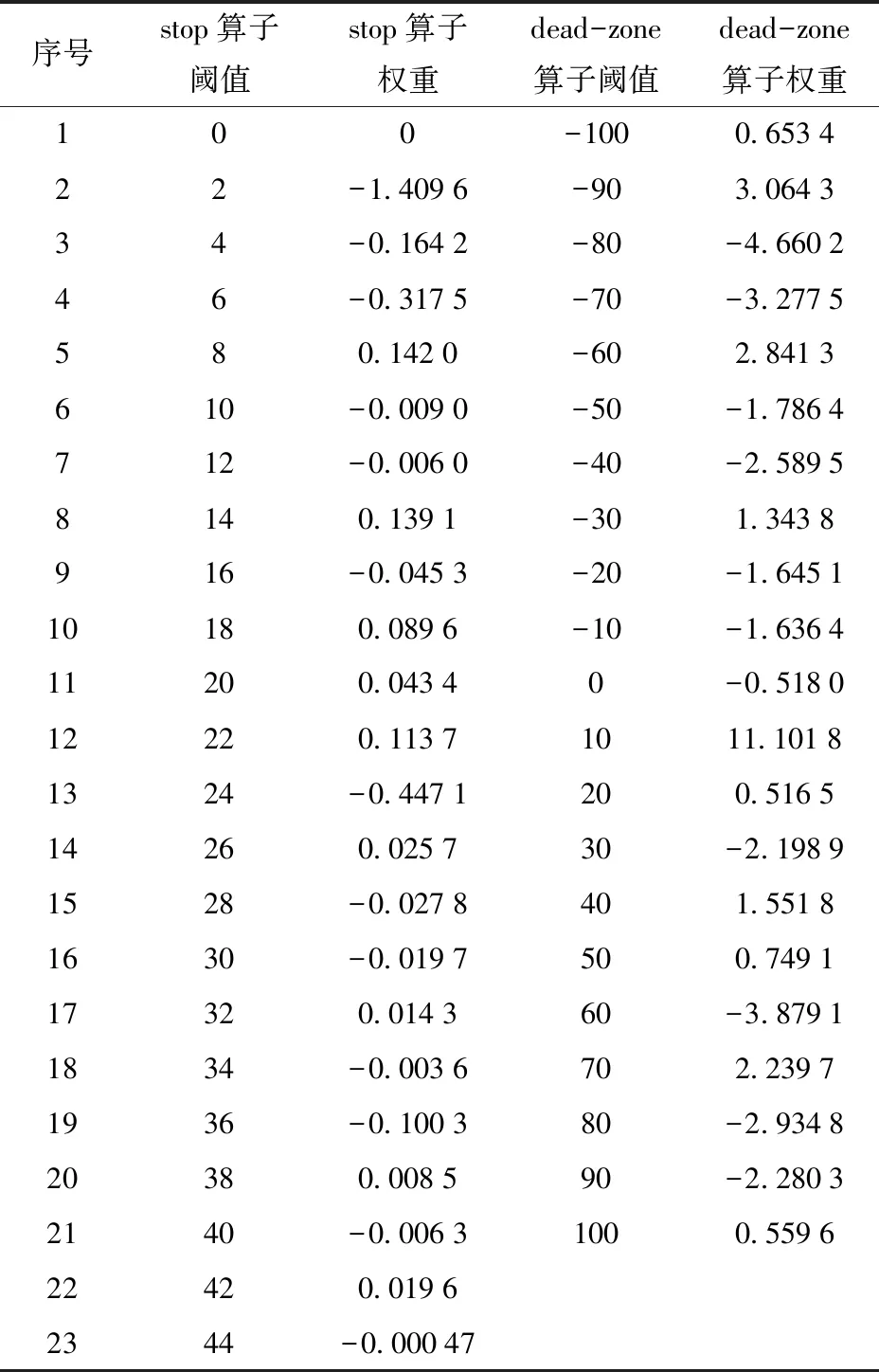
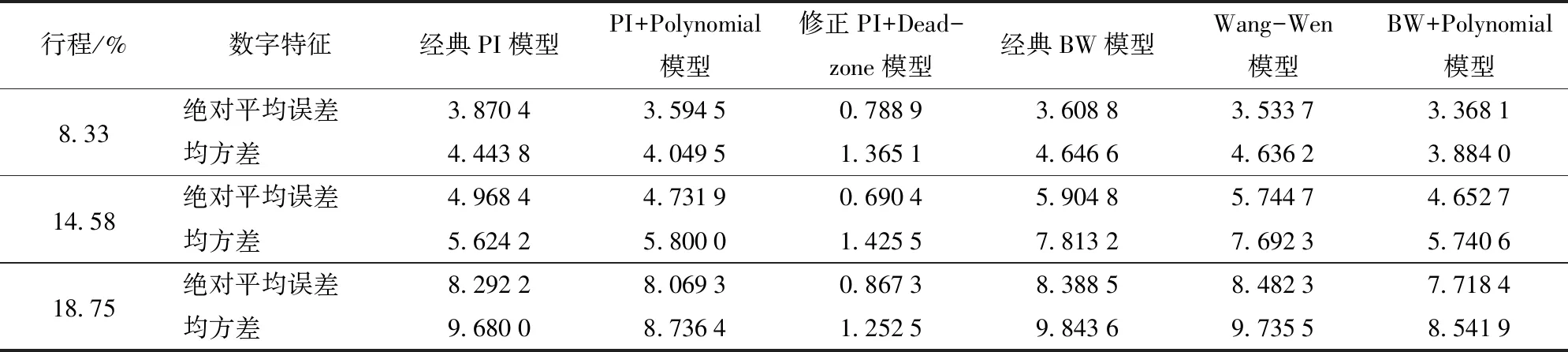
(9)

图11展示了修正PI+Dead-zone模型结构：经典PI模型的输出FPI作为修正dead-zone算子模型的输入，通过该方式，将stop算子与修正dead-zone算子相级联，修正PI+Dead-zone算子同原PI+Dead-zone类似具有非对称性，因此，级联后的修正PI+Dead-zone模型可以描述非对称迟滞现象。与经典PI模型类似，stop算子与修正dead-zone算子均具有率不相关性，加权叠加后，修正PI+Dead-zone模型继承了这一特点。

3 模型参数辨识及实验验证

3.1 气动肌肉收缩力测试装置

搭建图12所示气动肌肉收缩力测试台。被测气动肌肉(Festo DMSP-20-480N-RM-CM型)一端固定，另一端通过拉压力传感器(DYLY-103型)与负载气缸(AirTAC SC100-400LB型)相连。利用精密减压阀(CKD RP1000-8-07型)调节气动肌肉内部压力，并采用压力传感器(FestoSPTW-P10R-G14-VD-M12型)测量实时压力。通过比例方向阀(Festo MPYE-5-1/8-HF-010-B型)闭环控制负载气缸的活塞杆伸出长度，从而动态调节气动肌肉的收缩量。气动肌肉伸缩量/长度测量采用拉线式位移传感器(MIRAN MPS-S-100MM-P型)。比例方向阀控制信号的产生和各传感器信号的读取利用dSPACE DS1103完成。

动态收缩力是由收缩力测试台通过等压实验测得。测试过程中，调节精密减压阀将气动肌肉内部压力设定在某一值，然后通过闭环控制驱动气缸改变气动肌肉长度，获取气动肌肉收缩力与位移关系曲线。静态力是由等距实验拟合而来，先将气动肌肉两端距离固定于某一值(即收缩后长度固定)，对其充气至设定压力，记录此时气动肌肉的静态力和压力，放气后调整气动肌肉两端距离，重复上述过程即可获得静态力与压力的线性关系。进一步将斜率和截距与收缩率的关系通过适当阶次多项式拟合出来，从而得到完整的静态力模型。再将静态力从收缩力中减去，得到迟滞力与位移关系曲线。

3.2 模型参数辨识

保持气动肌肉压力为0.5 MPa，利用负载气缸使气动肌肉收缩率按幅值为8.33%、14.58%、18.75%的三角波变化，获得气动肌肉迟滞力Fh及气动肌肉长度l的实时数据，PI类模型利用最小二乘法进行参数辨识(BW类模型使用遗传算法)，选取准则函数J(θ)为

J(θ)=(Fh-Fm(θ))T(Fh-Fm(θ))

(10)

式中Fm(θ)——各迟滞模型输出迟滞力

Fh——连续时刻气动肌肉迟滞力测量值

θ——模型辨识参数

表1给出了经典PI模型、PI+Polynomial模型[10]、修正PI+Dead-zone模型、经典BW模型、Wang-Wen模型[23]、BW+Polyomial模型所需辨识参数θ。

表1 模型所需辨识参数Tab.1 Parameters for identification

受到篇幅限制，表2仅给出气动肌肉行程为18.75%的修正PI+Dead-zone模型辨识结果。

表2 修正PI+Dead-zone模型辨识结果Tab.2 Identification results of modified PI+Dead-zone model

3.3 模型精度分析

为合理量化模型精确度，引入各迟滞模型与实验数据间绝对平均误差emea及均方差erms作为评价指标。表3分别给出了行程为8.33%、14.58%、18.75% 6种模型的emea及erms。图13分别给出了3种行程下经典PI模型、PI+Polynomial模型、修正PI+Dead-zone模型、经典BW模型、Wang-Wen模型、BW+Polynomial模型模型的拟合结果。图13a表明经典PI模型能大致反映气动肌肉迟滞曲线变化趋势，且相比经典BW模型，经典PI模型的均方差erms比经典BW模型提高了4.4%(行程8.33%)、28%(行程14.58%)、1.6%(行程18.75%)，这说明经典PI模型更能反映气动肌肉力-位移迟滞曲线趋势。原因可从两方面分析：从宏观上可以看出，气动肌肉力-位移迟滞曲线在形状上呈不规则多边形形状，经典BW模型迟滞曲线形状关于曲线中心对称且与其差异较大；从模型构成机理上分析，鉴于气动肌肉力-位移迟滞现象的非局部记忆性，气动肌肉力-位移迟滞曲线形状明显受到气动肌肉长度的影响，而模型迟滞曲线形状控制函数与模型输入气动肌肉长度无关。图13c表明修正PI+Dead-zone模型能反映气动肌肉力-位移迟滞现象所有的非对称信息，模型拟合效果极好，各行程下绝对平均误差不超过1 N，均方差不超过1.5 N，仅就对称性最差的大行程工况(行程18.75%)，较经典PI模型、PI+Polynomial模型、经典BW模型、Wang-Wen模型、BW+Polynomial模型，修正PI+Dead-zone模型的绝对平均误差emea分别提高了89.5%、89.25%、89.7%、89.8%、88.7%，其均方差erms分别提高了87.0%、85.7%、87.3%、87.1%、85.3%。从图13c直观看出，修正PI+Dead-zone模型解决了其他模型大行程下迟滞拟合精度较差的问题，其原因在于经典PI模型及经典BW模型均为对称迟滞模型，无法描述非对称迟滞现象；Wang-Wen模型仅能描述迟滞曲线拐点关于迟滞曲线中心不对称的迟滞现象，其描述非对称迟滞现象的能力十分有限；PI+Polynomial模型与BW+Polynomial模型无法找到一个适合阶次的多项式来准确反映各行程下气动肌肉力-位移迟滞现象的非对称信息。在行程不大的情况下，经典PI模型也能达到一定的建模精度，绝对平均误差emea为3.870 4 N(行程8.33%)、4.968 4 N(行程14.58%)，且模型参数相比修正PI+Dead-zone模型参数大大减少。

表3 6种迟滞模型的数字特征Tab.3 Indexes of six hysteresis models under stroke N

将来，可进一步将建立的气动肌肉修正PI+Dead-zone模型用于气动肌肉伺服系统控制器的设计，尤其是以单关节气动肌肉为驱动的并联平台及相关仿人机器人系统。工程中相关气动肌肉系统常以比例方向阀或高速开关阀控制，其整个系统动态模型相对阶为3阶，整个系统具有强非线性，常用基于反步法的控制策略非线性控制器。反步法要求各模型项至少一阶连续可导，而PI类迟滞模型在本质上均是泛函概念且不连续，在设计包含气动肌肉力-位移迟滞模型的非线性控制器时导致模型不确定性无界或者虚拟控制输入无法求导，虽然现阶段相关控制理论研究有一定的手段处理此类问题，但就精度最高的修正PI+Dead-zone模型，由于其stop算子与修正dead-zone算子级联特点，其在解决迟滞模型项不可微问题上的复杂度远大于经典PI模型。如果在控制器设计中考虑参数自适应，对修正PI+Dead-zone模型两类算子权重全部进行在线辨识，其两类算子权重辨识算法很难设计或在牺牲一部分系统控制精度上才能满足参数收敛性要求，由此导致控制器设计难度大大增加；若在参数自适应中仅在线辨识修正dead-zone算子权重，又由于修正PI+Dead-zone模型级联特点，其控制器设计复杂性也远大于经典PI模型。因此，气动肌肉处于小行程工况，进行迟滞补偿的非线性控制器设计可以选择经典PI模型。

4 结论

(1)搭建了气动肌肉收缩力测试平台，通过气动肌肉动态拉伸实验得到气动肌肉力-位移迟滞曲线，通过分析气动肌肉力-位移迟滞曲线，证明气动肌肉力-位移迟滞现象具有非对称性、非局部记忆性、大压力弱相关性及准率不相关性。

(2)PI类迟滞模型比BW类迟滞模型更能反映气动肌肉力-位移迟滞曲线变化趋势，经典PI模型的均方差erms较经典BW模型提高了4.4%(行程8.33%)、28%(行程14.58%)、1.6%(行程18.75%)。

(3)气动肌肉修正PI+Dead-zone模型精度最高，各行程下绝对平均误差emea不超过1 N，均方差erms不超过1.5 N。建立的气动肌肉修正PI+Dead-zone模型能极好拟合各行程下的气动肌肉力-位移迟滞曲线，特别对大行程下的非对称迟滞曲线有显著效果。

(4)在小行程工况下，气动肌肉经典PI模型也能相对准确描述其力-位移迟滞现象，其绝对平均误差emea为3.870 4 N(行程8.33%)、4.968 4 N(行程14.58%),且具有比修正PI+Dead-zone模型的模型参数少的优点。