考虑非线性摩擦的绳驱动连续体机器人动力学研究

齐 飞 佘世刚 高书苑 陈 柏 吴洪涛

(1.常州大学机械与轨道交通学院， 常州 213016； 2.南京航空航天大学机电学院， 南京 210016)

0 引言

连续体机器人具有独特的柔顺性、安全性和灵活性，能在一些曲折、狭小的工作环境中作业，因此在工业管道、航空发动机及医疗手术等领域得到了广泛研究。建立高效、准确的运动模型是机器人运动控制的基础和前提条件，但连续体机器人是一种超冗余、强耦合的非线性系统，获取其适用的数学模型难度较大。为了实现对连续体机器人精确的运动控制，需要对其进行动力学建模研究。

一般情况下，连续体机器人的变形过程可以通过运动学模型进行描述，但在受到外界环境干扰及运动速度较大时，运动学模型将无法准确地表示机器人的动态变形过程[1-5]。常见的动力学建模方法有拉格朗日法、牛顿欧拉法和凯恩法[6-9]。HE等[10]基于拉格朗日法建立了多节连续体机器人的动力学模型，但忽略了传动摩擦损失的影响。RONE等[11]基于虚功原理推导了连续体机器人动力学模型，同时对驱动绳与连接盘间的摩擦影响进行了研究。WANG等[12]基于融合的Cosserat梁理论和凯恩方法建立了一种绳驱动的软体机器人动力学模型，该模型考虑了软体材料粘性变形所带来的阻尼作用。RENDA等[13]基于几何分析法推导了仿象鼻软体机器人的动力学模型，并分析了关节耦合力与外界相互作用力的影响。XU等[14]针对一种绳驱动冗余机械臂进行了运动学和动力学建模，并提出了一种驱动解耦方法。XU等[15]基于分段分析法推导了一种杆驱动软体机器人的静力学模型，并通过几何相容性约束和椭圆积分法分析了机器人的运动和刚度特性，但这种方法建模复杂，且需要进行多次积分。

本文针对自主研发的介入手术连续体机器人的运动模型及控制策略进行研究。首先，基于几何分析法对运动学模型进行分析，构建考虑惯性力、弹性内力、重力及驱动力影响的动力学模型；分析绳-轮传动系统的非线性摩擦对运动传递的影响，提出一种基于误差补偿的前馈控制策略；最后通过仿真和实验对所建模型和控制方法的有效性进行验证。

1 连续体机器人运动模型

图1为本文所提出的一种绳驱动连续体机器人，该机器人主要由NiTi合金芯柱、连接盘、硅胶外壳等组成。连接盘等间距固定在芯柱上，每个连接盘圆周上均匀分布3个导向孔。驱动绳通过导向孔后固定在机器人末端，通过调节驱动绳长度来实现机器人在三维空间中的变形运动[16]。为方便建模，假设机器人质量和惯性由连接盘、芯柱质量和惯性所决定，忽略了弯曲过程中机器人扭转和剪切应变。

如图2所示，每段弯曲单元用参数β、θ来表示，其中β为弯曲切面方向角，θ为弯曲角，定义向量qi=(θi,βi)T来描述图2b所示的坐标系，则对于n个单元的连续体机器人有

(1)

在分段常曲率圆弧假设下基于几何分析法建立第i个连接盘中心相对于前一坐标的位置向量为

i-1pi=(cβi(1-cθi)l/θi，sβi(1-cθi)l/θi，sθil/θi)T

(2)

式中l——弯曲单元长度

pi——位置向量

其中s表示sin,c表示cos。

其中当弯曲角为0时，为避免矩阵变换陷入奇异性(分母为0)，令pi=(0,0,l)T。

而第i个坐标系的方向则由3个欧拉变换矩阵组成(图2b)，分别为绕前一坐标系zi-1轴旋转βi，绕当前坐标系y1轴旋转θi，最后再绕zi轴旋转-βi。

(3)

则第i节弯曲单元相对于基坐标系的位姿变换矩阵Ti为

(4)

其中R1=0R1P1=0P1

Ri=Ri-1i-1RiPi=Ri-1i-1pi+Pi-1(i>1)

式中Pi——第i节弯曲单元相对于基坐标系的位置向量

Ri——第i节弯曲单元相对于基坐标系的旋转矩阵

若已知机器人末端位姿，则关节空间与操控空间的逆变换为

(5)

根据几何分析法，则关节空间到驱动空间的映射关系为

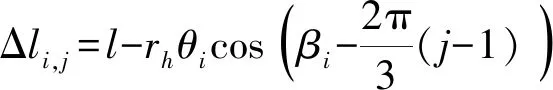
(i=1,2,…，n;j=1,2,3)

(6)

式中rh——驱动绳孔半径

Δli,j——第j根绳长的变化量

相邻坐标系间的速度可分别通过位置变换向量i-1pi和旋转变换矩阵i-1Ri对时间求导得出，其中线速度可直接通过对位置向量求导得出，即

(7)

式中i-1vi——线速度

Jxv——线速度对应的雅可比矩阵

但直接对旋转变换矩阵i-1Ri求导比较复杂，可通过欧拉变换原理求解当前坐标系相对于前一坐标系的角速度。

令旋转变换矩阵i-1Ri每一列分别对应切向量i-1ti、法向量i-1ni、副法线向量i-1bi，即i-1Ri=[i-1nii-1bii-1ti]，则当前坐标系下机器人的角速度由式(8)可得

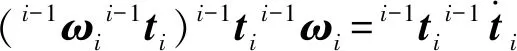
(8)

将式(8)展开并化简得角速度为

(9)

式中i-1ωi——角速度

Jxω——角速度对应的雅可比矩阵

对于n段连续体机器人，其末端连接盘相对于初始坐标系的速度为

(10)

其中

式中Jn——n节连续体机器人的雅可比矩阵

Ji——第i节弯曲单元对应的雅可比矩阵，i=1,2,…,n

Ai——第i节弯曲单元对应的伴随矩阵

而第i节弯曲单元相对于基坐标系的线加速度ai和角加速度ψi可通过对线速度和角速度相对于时间求导得出，即

(11)

(12)

2 连续机器人动力学模型

为分析连续体机器人的动态变形特性，基于凯恩方法对机器人进行动力学建模。为简化模型，忽略了机器人在运动过程中的剪切、扭转及压缩等变形，只考虑机器人的弯曲变形运动。

2.1 弹性力分析

根据Cosserat梁理论[17-18]，当机器人弯曲变形时其中心骨架产生的弯曲和扭转应变可由曲率向量Ki表示，则第i段弯曲单元在弯曲过程中产生的弹性势能密度Ep为

其中

(13)

式中E——杨氏模量G——剪切模量

Ii——截面惯性矩Ipi——极惯性矩

(14)

考虑到相邻关节间的耦合影响，则第i个离散单元的弹性力矩Mi,el为

(15)

2.2 重力分析

根据前文假设，第i段弯曲单元所受的重力Fi,g表示为

(16)

式中mi——第i段弯曲单元质量

g——重力加速度

2.3 驱动力分析

如图3所示，每个连接盘具有3个导向绳孔，且相邻连接盘间的驱动绳为直线，则驱动绳的运动方向可由连接盘导向孔的方向决定。在当前坐标系下，连接盘的3个导向孔的位置向量为

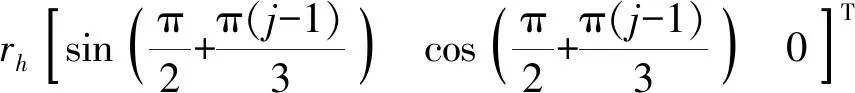
(j=1,2,3)

(17)

根据式(17)，则驱动绳张力的方向可通过驱动绳位置向量pi,j的单位向量表示为

fi,j=pi,j/‖pi,j‖

(18)

其中

(19)

式中fi,j——第i连接盘第j根绳张力向量

第i连接盘第j根绳的张力Fi,j为

(20)

最终施加在每个连接盘上的等效驱动力Fi,act及驱动力矩Mi,act为

(21)

2.4 惯性力分析

根据式(10)～(12)求解出的速度及加速度，则每个连接盘所受到的惯性力Fi,inr和惯性力矩Mi,inr为

(22)

其中

式中IIi——连接盘的转动惯量

Ixx、Izz——径向和轴向转动惯量

2.5 动力学模型

根据凯恩(Kane)方法[19-20]，机器人系统在外力和外力矩下所做的虚功P(式(23))为0时从而推导出机器人的动力学模型。假设机器人每个离散的弯曲系统所受的外力和外力矩分别为Fi,ex、Mi,ex，结合由式(10)得出的对应角速度和线速度，则连续体机器人系统的动力学模型为

(23)

(24)

其中

Fi,ex=Fi,inr+Fi,g+Fi,act

Mi,ex=Mi,inr+Mi,act

为了便于分析，可将式(24)简化为一般形式的动力学模型，即

(25)

其中

式中H(q)——机器人惯性矩阵

G(q)——机器人自身重力和中心骨架的弹性力

Q——等效广义力

3 动力学模型仿真

以一个由4节离散单元组成的绳驱动连续体机器人为仿真对象，分别在静态平衡和弯曲运动状态下对机器人的动态性能进行分析，通过求解该模型的数值解来验证所建动力学模型的正确性。机器人材料特性和结构参数如表1所示。

表1 材料与结构特性参数Tab.1 Material and structure parameters

3.1 静态平衡时

首先研究未加负载时机器人的动态特性，即驱动张力为0。令θi=0.000 1 rad、βi=0 rad作为数值求解动力学模型时的初始关节参数。由于输入张力为0，机器人理论上处于静态平衡状态，即广义速度及加速度均为0。图4为零驱动状态下机器人各离散关节参数的动态特性。由图4可知，零驱动时，连续体机器人各离散单元弯曲角θ随时间的变化规律为绕某一固定值的正弦曲线，而旋转角随时间变化始终为0。同时由于各驱动绳的输入张力为0，系统总能量始终保持不变。而图4b展示了零驱动时连续体机器人的运动形状为绕某一平衡位置做振荡运动。

3.2 弯曲运动时

考虑到机器人在三维空间中相互对称运动特性，对弯曲运动时机器人的动态特性进行分析。假设机器人初始驱动张力为T1=5 N,T2=0 N,T3=0 N，以各个关节参数θi=π/12,βi=0.001 rad作为求解动力学模型的初始值，则运动过程中连续体机器人各关节弯曲角的动态变化如图5所示。由图5可知，机器人在单一驱动力下做平面运动，则旋转角βi始终为0。由图5a可知，从前至后各离散弯曲单元的弯曲角幅值依次减少，并最终收敛于某一稳定位置，这可能是由于传动系统中的摩擦所引起的。而图5b则展示了运动过程中机器人中心骨架的形状随时间呈振荡变化，且最终收敛于弯曲角为π/6的平衡位置。

4 导向轮间传动特性分析

在实际运动过程中驱动绳索需要通过导向轮后与伺服电机转轴相连(图6)，则绳-轮传动系统中的摩擦力势必会对张力的传递造成影响，从而降低机器人的运动精度。

由文献[21-22]可知，驱动绳与导向轮间摩擦力与接触面正压力满足能量法则

f=αNn(n≤1)

(26)

式中f——摩擦力N——法向力

α、n——常量，与接触材料特性有关

结合图6，则驱动绳与导向轮间的绳张力、剪切力和弯曲力矩的平衡方程为

(27)

由于dφ→0，将式(27)化简可得

(28)

式中T——绳张力Q——剪切力

M——剪切力矩

φ——传动系统微小包角

r——驱动绳半径

Rp——导向轮半径

由于所采用的驱动绳为超高分子聚乙烯编制的PE线，由文献[23-25]可知，驱动绳与导向轮在运动过程中将产生粘弹性的变形。假设ρ=Rp/r为接触面半径，将式(26)代入到方程(28)中，可得

(29)

式(29)为考虑了弯曲刚度和非线性摩擦力影响的改进Capstan方程，该模型能够准确地描述驱动绳与导向轮间的粘弹性变形。为便于求解，通过Matlab中的ODEs函数来解其数值解。首先将微分方程转换为1阶微分的形式，即

(30)

假设绳-轮传动系统总包角φ=[0，π]，绳-轮半径比ρ为1或10，接触摩擦力系数α为0.15或0.6，参数n为0.67或1。若假设经绳-轮传动系统后的初始输出张力为1，则在运动过程中传动系统输入和输出张力的比值随包角的变化规律如图7所示。由图7可知，随着接触包角的变大，绳-轮传动系统的能量损耗越大，即输入到系统中的绳张力也越大。与经典的Capstan方程相比，考虑非线性摩擦及弯曲刚度的改进模型的摩擦损失小，且其张力比随弯曲度的变化相对比较平稳，即在输出相同张力时所需的绳输入张力小。同时分析了不同参数对绳-轮传动模型的影响，对比图7a、7b可知，改进后的传动模型中绳张力损失较小，且非线性摩擦对张力损耗的影响比弯曲刚度的大。当摩擦力系数α为0.6时，输入和输出的绳张力比比摩擦力系数α为0.15时变化快，表明摩擦力系数是影响传动效率的最主要参数。

5 实验验证

为验证所建模型及所提控制方法的有效性，根据图8所示的机器人运动控制框图搭建了单节连续体机器人样机平台，如图9所示。该机器人本体由一个直径为0.8 mm的NITi合金芯柱、5个3D打印的外径为10 mm的连接盘、硅胶外壳和4根直径为0.8 mm的大力马聚合编织的绳组成。机器人的材料特性如表1所示。机器人总长度为90 mm，直径为10 mm，弯曲所需的驱动力主要由3个Maxon电机(A-max22, Switzerland)提供，同时每根驱动绳均连有一个张力传感器(JLBS-MD-10kg)，用于测量运动过程中绳的实际张力。通过Matlab/Simulink编写相应的控制程序，并基于RTW/xPC实时控制平台控制机器人的变形运动，从而来验证机器人运动模型及控制方法的有效性。

5.1 平面内的弯曲运动

首先控制连续体机器人在单一平面xz内进行弯曲运动(图10)，则机器人仅在驱动绳1张力作用下进行平面弯曲运动，其他绳张力均为0。根据所建的运动模型，则在运动过程中机器人的理论运动轨迹及驱动绳长的变化量如图11a、11b所示。由图可知，连续体机器人的末端运动轨迹为一椭圆弧曲线，且在平面内以同一弯曲角速度0.26 rad/s进行弯曲运动。而图11c、11d展示了运动过程中连续体的理论驱动力和实测驱动力。由图可知，该机器人仅在驱动绳1张力F1作用下进行弯曲运动，其余绳张力均为0。同时根据图11d理论驱动绳张力与实测输入驱动力间的误差可知，其张力损失量随着机器人弯曲角的增大而增大，当弯曲角为1.6 rad时，最大驱动力偏差为1.26 N，可能是机器人加工误差所引起，但占比较小，可忽略不计。

5.2 空间内的圆弧运动

假设机器人在三维空间的圆弧轨迹为

(31)

其具体的运动过程如图12所示。首先根据运动学模型可得机器人理论运动轨迹，如图13a所示，而运动过程中关节参数和驱动绳长随时间的变化曲线如图13b、13c所示。由图可知，连续体机器人在三维空间中以旋转角速度0.53 rad/s，恒定的弯曲角π/3作圆弧运动。由图13d、13e可知，连续体机器人在弯曲运动中所需的理论驱动力基本上与实际施加的驱动力一致，但存在一定量的偏差(理论驱动力略小于实际输入驱动力)，其主要原因是用于补偿绳-轮传递系统中摩擦力所引起的绳张力损耗。运动过程中绳驱动的张力损失如图13e所示，同时该误差也包含了加工误差和装配误差所引起的张力损失，由于这项误差较小(均值均为0.42 N)可忽略不计。但从实验结果可知，所提的动力学模型基本上能够较为精确地描述连续体机器人的动态运动过程。

6 结论

(1)所建立的动力学模型能够准确地描述机器人的动态变形过程，并通过实验进行了验证。但在运动过程中，机器人实际电机输入驱动力略大于理论驱动力，其主要原因是需要补偿运动过程中绳-轮传动系统的摩擦损失。

(2)实验结果同时也验证了运动学建模时的常曲率圆弧假设，忽略了连接盘间距参数对连续体机器人运动学建模误差的影响。

(3)连续体机器人理论弯曲形状与实际形状间存在微小偏差，这可能是由制造加工误差及装配误差等导致，可忽略不计。