基于工作空间的果园作业平台结构参数优化与试验

樊桂菊 李 钊 毛文华 娄 伟 梁 昭 姜红花

(1.山东农业大学机械与电子工程学院， 泰安 271018； 2.山东省农业装备智能化工程实验室， 泰安 271018；3.山东省园艺机械与装备重点实验室， 泰安 271018； 4.中国农业机械化科学研究院， 北京 100083；5.山东农业大学信息科学与工程学院， 泰安 271018)

0 引言

水果种植属于劳动密集型产业。为降低剪枝、疏花疏果、采摘等作业环节的劳动强度，提高工作效率，学者们研制了多种类型辅助人工操作的果园作业平台[1-4]，根据升降机构的不同，作业平台可分为剪叉式和臂式。水果种类繁多，各地种植模式不同[5]，果园作业平台的工作空间直接影响其适用性。因此，开展基于工作空间的果园作业平台结构参数优化研究对其推广应用具有重要意义。

针对考虑工作空间的结构参数优化问题，吴超宇等[6]以提出的全局混合性能指标为目标函数，利用粒子群算法优化得到直线驱动型并联机器人的最优尺寸参数。权龙哲等[7]以包容目标工作空间及杆长因素为目标，采用遗传算法优化立体苗盘管理机器人的结构参数。丁渊明等[8]提出以工作空间和能量消耗综合指标为目标函数，使用遗传算法优化机械臂结构参数。孙小勇等[9]通过分析并联机构结构尺寸对工作空间的影响确定了结构参数的优化范围，利用fminimax函数求解得到优化后的结构参数。

基于工作空间的结构参数优化主要集中在机器人或机械臂等方面，针对果园机械的相关研究较少。本文基于已研制的果园作业平台，以乔砧密植的纺锤形苹果种植模式确定其目标工作空间，采用网格迭代算法计算可达工作空间体积，分析平台结构参数对其空间性能的影响规律，建立以空间性能和结构紧凑为指标的多目标优化函数，利用遗传算法求解最优参数，并通过仿真与试验进行验证，以期提高果园作业平台的适用性和可操作性。

1 果园作业平台工作空间分析

1.1 运动学模型

前期研制的果园作业平台主要由动力装置、行走机构、回转机构、升降机构、调平机构、工作台和控制系统等组成，实现工作台升降、旋转和坡地调平等功能。其结构、工作原理和运动学方程见文献[10]，但未考虑操作人员在工作台的左右和前后移动。为更好地描述平台可操作性和各机构运动，将原参考点在竖直方向上移动至成人肩高[11]位置作为平台执行末端参考点，建立D-H坐标系[12-13]，如图1所示。其中，l1～l5为各杆长度，分别为964、812、210、900、680 mm。各参数如表1所示，表中αi、ai、di、θi(i为关节编号，i=1,2,…,6)分别表示连杆转角、连杆长度、连杆偏移和关节角。d5min为工作台铰接点安装距离，为70 mm；d6max与d6min互为相反数，使工作台关于横梁对称以保持平衡。其运动学方程为

(1)

其中

P=[pxpypz]T

式中R——姿态矩阵P——位置矩阵

n、o、a、p——关于θi与di的函数

O——零矩阵

表1 果园作业平台D-H参数Tab.1 D-H parameter of orchard platform

1.2 目标工作空间

果园作业平台的目标工作空间是其结构参数设计和优化的重要依据，与果园地形、果树种类和种植模式密切相关。而我国果树种类繁多，种植模式各异，为使作业平台能够灵活、高效地在复杂环境中进行升降、旋转和调平等动作，实现辅助人工完成剪枝、疏花疏果、套袋及果实采摘等作业环节，结合作业平台的通用性，本文以种植面积位居前列的苹果为研究对象，目前其种植模式仍以乔砧密植为主，树形多为纺锤形[14-15]，株距为3～4 m，行距4～5 m，株高为2.8～3.5 m，主干高度为0.6～1.0 m，冠径为1.4～3.0 m。以O0为坐标原点，X轴为行距方向，Y轴为平台前进方向，Z轴为株高方向，平台参考点的目标工作空间如图2所示。其中，阴影部分为平台参考点的目标工作空间；Dtx、Dty、Dtz分别表示目标工作空间在X、Y、Z方向范围，分别为[-((L0-Ld)/2-Lr)，(L0-Ld)/2-Lr]、(0，D0/2-Lr]、[Hr+Lr，Hs-Lr]，其中L0为行距，Ld为冠径，D0为株距，Hr为成人肩高，Hs为株高，Lr为成人掌心与肩膀距离。

为使平台最大限度地满足作业需求，各参数取值为：L0、D0、Hs分别取最大值，冠径取最小值，由文献[11]可知，成人掌心与肩膀距离取0.5 m，肩高取1.4 m。得目标工作空间在X、Y、Z方向范围分别为：Dtx为[-1 300 mm,1 300 mm]、Dty为(0,1 500 mm]、Dtz为[1 900 mm,3 000 mm]。

1.3 可达工作空间

平台参考点的可达工作空间指在各关节约束下参考点运动学方程所有解的集合。本文采用改进的蒙特卡洛法[10]得到其工作空间点云图，如图3所示。由图3可知，参考点可达工作空间在X、Y、Z方向范围分别为：Drx为[-1 781 mm,1 802 mm]、Dry为[-730 mm,1 819 mm]、Drz为[1 190 mm,2 917 mm]。

2 可达工作空间性能指标

2.1 工作空间尺寸偏差

由上文可知，作业平台参考点的可达工作空间与目标工作空间存在偏差，X方向和Y方向偏差可以通过调整平台底盘位置消除，因此本文仅研究Z方向偏差。

对比图2和图3，为保证操作人员对两行果树有效作业，以μz1和μz2描述平台工作空间尺寸偏差，计算式为

(2)

式中Zr1max、Zr1min——X为-1 300 mm时可达工作空间中Z的最大值、最小值，mm

Zr2max、Zr2min——X为1 300 mm时可达工作空间中Z的最大值、最小值，mm

Ztmax、Ztmin——目标工作空间在Z方向的最大值、最小值，mm

2.2 工作空间体积

工作空间体积[16]是表述作业平台工作能力的重要参数。为得到较高精度的空间体积，本文采用网格迭代算法[17]。设某子网格编号为Numi，其相邻网格编号如图4所示，算法流程如图5所示。

通过多次迭代计算平台参考点的工作空间体积，体积迭代差计算式为

(3)

式中Vj、Vj-1——第j、j-1次迭代工作空间体积，m3

以体积迭代差ε≤0.1%为体积收敛标准。图6为工作空间体积迭代变化曲线，第16次迭代时体积迭代差为0.045%，故取工作空间体积为4.26 m3。

2.3 平均可操作度

为量化作业平台在X、Y、Z方向的运动能力，以平台可操作性作为评价参数。目前关于机器人可操作性的研究方法主要有：基于雅可比矩阵、基于Hessian矩阵和基于刚度矩阵[18-20]，其中由于雅可比矩阵代表了机器关节空间的微分运动向操作空间的微分运动之间的映射转换，而被广泛应用。因此，本文在平台参考点运动学模型基础上推导雅可比矩阵，计算式为

(4)

其中

D=[dxdydzδxδyδz]TJ=[J1J2J3J4J5J6]Θ=[θ1θ2θ3θ4d5d6]T

(5)

式中D——参考点沿X、Y、Z轴的微分平移和绕X、Y、Z轴的微分旋转矩阵

J——雅可比矩阵Θ——关节空间

基于雅可比矩阵有多种指标可以描述平台可操作性，其中可操作度κ考虑了机构执行末端的各方向运动能力而优于其他指标[21]，计算式为

(6)

式中λi——矩阵JJT的特征值

由式(4)、(6)可知，当平台结构参数给定后，可操作度随平台参考点空间位置变化而不同，为描述作业平台在工作空间的全局操作性能，引入平均可操作度τ，计算式为

(7)

其中Ω={(x,y,z)|x∈Drx,y∈Dry,z∈Drz}

式中Vi——平台可达工作空间子网格空间体积，m3

V——平台可达工作空间体积，m3

Ω——平台可达工作空间范围，m

2.4 结构参数对可达工作空间性能的影响

通过分析果园作业平台运动学模型和其工作空间，影响其空间性能的结构参数主要是杆长和关节变量(关节角和连杆偏移)。根据其结构特点及作业要求，主要分析杆2、4长度，关节1、3关节角，以及关节5、6连杆偏移对空间性能的影响规律。

2.4.1杆长

保持关节变量和杆1、3、5长度不变，杆2、4长度在0～1 600 mm之间变化，通过蒙特卡洛方法多次模拟可达工作空间，由2.1～2.3节分别得杆2、4对可达工作空间尺寸偏差μz1和μz2、体积V及平均可操作度τ的影响，如图7所示。

由图7可知，杆2、4对μz1和μz2影响趋势一致，杆2影响更大：当杆2长度约为950、960 mm时，μz1和μz2最小，分别为42.82、40.05 mm；当杆4长度约为800、810 mm时，μz1和μz2最小，分别为260.49、258.97 mm；杆2对V和τ影响较小，杆4对V和τ影响较大且呈正相关。

2.4.2关节变量

保持杆长和关节2、4关节角不变，关节1、3的关节角分别在[60°,300°]和[-130°,-50°]范围内变化；由表1可知，d5min为70 mm，|d6max|=|d6min|，故仅考虑d5max、d6max对工作空间的影响，关节5、6的连杆偏移最大值在[0,1 200 mm]范围内变化。得关节1、3的关节角和关节5、6的连杆偏移对可达工作空间性能的影响，如图8～10所示。

由图8～10可知，θ1对μz1、μz2影响较小，当θ3为-111°～-63°时，μz1和μz2最小，分别为62.18、54.74 mm；θ1与θ3对V影响较大，对τ影响较小但均呈正相关。当d5max大于700 mm时，μz1和μz2基本不再变化；当d6max大于800 mm时，μz1和μz2基本不再变化；d5max对V和τ均影响较大呈正相关；d6max对V影响较大呈正相关，对τ影响较小呈负相关。

3 结构参数优化

3.1 优化模型

针对复杂的果园作业环境空间，为使作业平台能够安全可靠地完成动作，在能够满足目标工作空间的作业要求下，执行升降、旋转和调平任务时更加灵活、高效，可达工作空间与目标工作空间的尺寸偏差应尽量小，空间体积和平均可操作度应尽量大。因此可达工作空间性能目标优化函数为

(8)

式中w——待优化参数矩阵

同时，为使作业平台结构更加紧凑，在满足目标工作空间作业任务前提下，平台结构尺寸和关节变量应尽量小，即总杆长和关节变量总和应尽量小。因此结构紧凑目标优化函数为

(9)

式中ζ1、ζ2——量纲统一系数

根据2.4节的分析和上述目标优化函数涉及的变量可得出平台待优化的参数为杆2、4长度，关节1、3关节角范围和关节5、6连杆偏移范围，用矩阵w表示为

w=[l2l4θ1maxθ1minθ3maxθ3mind5maxd6max]T

(10)

综上所述，作业平台结构参数优化函数共有6个子目标，8个待优化参数，属于多元多目标函数优化问题，引入比例因子和权重，将其变为单目标优化函数；由图7～10得到待优化结构参数范围作为约束条件，优化模型为

(11)

其中

∑ηi=1

式中fi(w)——各子目标函数

F(w)——总目标函数

si——比例因子ηi——权重

3.2 优化过程

根据平台原有结构和实际作业需求，对优化模型的各指标设定适当的比例因子和权重。

3.2.1比例因子

工作空间尺寸偏差越小越好，考虑优化精度和实际作业情况，其比例因子取10 mm；工作空间体积、平均可操作度及结构参数指标的比例因子均以原样机结构为基础，分别按照前述对应内容计算求解，结果如表2所示。

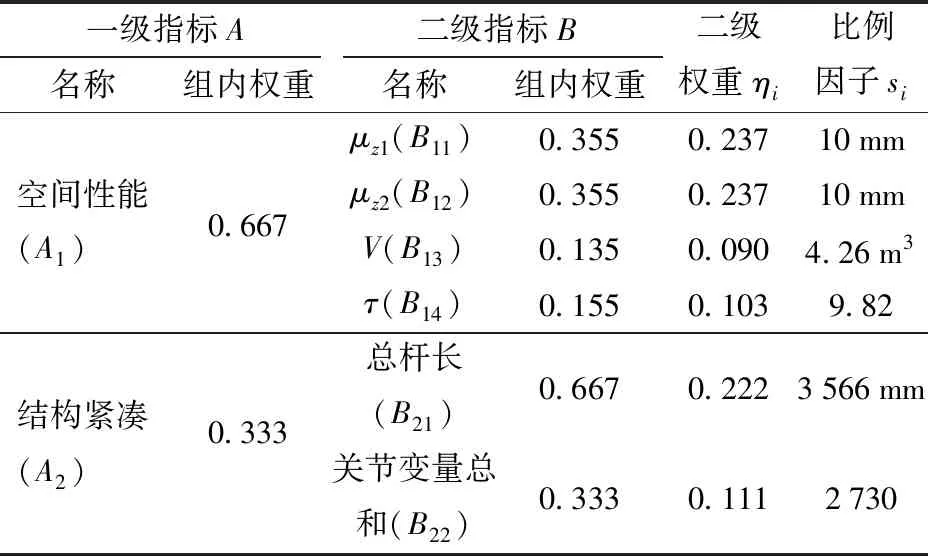
表2 子目标函数指标权重及比例因子Tab.2 Index weight and scale factor of sub-objective function

3.2.2权重

基于果园种植模式和优化模型，在能够完成作业任务的前提下，考虑农机农艺融合和人机工程学，各指标权重确定原则如下：①空间性能指标较结构紧凑指标更为重要。②在空间性能指标中，工作空间尺寸偏差最重要，μz1、μz2为同一性质优化指标，二者同等重要。③为保证平台灵活高效地完成执行动作，平均可操作度较工作空间体积更为重要。④通过分析图8～10中杆长和关节变量对工作空间尺寸偏差的影响，前者大于后者，因此杆长较关节变量重要。

以工作空间性能和结构紧凑为一级指标，6个子目标函数为二级指标。在上述原则前提下，采用德尔菲法[22]征询相关领域专家意见，同时结合层次分析法[23-24]的分析计算，最终确定各评价指标的权重。以空间性能(A1)为准则的二级指标μz1(B11)、μz2(B12)、V(B13)和τ(B14)为例，其步骤如下：

(1)将专家对各指标重要性评分汇总，依据判断矩阵标度[25]对指标B11～B14进行两两判断，构造出判断矩阵EA1，计算式为

(12)

(2)将上述矩阵每一行元素相乘得积为PA1i，对其归一化处理，即得权重ηA1i计算式为

(13)

(3)为保证专家对指标B11～B14重要程度的判断一致，以一致性比率CR检验判断矩阵的一致性，计算式为

(14)

式中RI——随机指标，判断矩阵4阶时RI取0.89[26]

根据以上步骤，将判断矩阵EA1和权重ηA1代入式(14)，得CR=0.057<0.1，即判断矩阵通过一致性检验，ηA1=[0.355 0.355 0.135 0.155]T。

同理，按上述步骤计算其余指标权重，结果如表2所示。

3.3 优化结果

将表2的数据代入式(11)，并将其编译为适应Matlab遗传算法工具箱的适应度函数，将优化模型的约束条件编译为适应于算法工具箱的区域描述器。设置初始种群个体数目为40，遗传代数为200，交叉概率为0.7，变异概率为0.007。运行算法得到适应度函数进化曲线如图11所示。

由图11可知，适应度函数约在第50代收敛。考虑实际加工因素，规整优化参数，如表3所示。

将优化前后参数代入运动学模型，模拟可达工作空间，分别计算其空间性能指标、总杆长和关节变量总和，结果如表4所示。

表3 优化前后结构参数对比Tab.3 Comparison of structural parameters before and after optimization

表4 优化前后指标对比Tab.4 Comparison of index before and after optimization

由表4可知，优化后可达工作空间最大偏差仅为12.33 mm，平均可操作度提高1.43%，表明优化后更接近目标工作空间，且操作更灵活。

4 试验与结果分析

4.1 试验条件

4.1.1试验准备

基于优化后的果园作业平台结构参数改进样机，于2020年7月在山东农业大学园艺实验基地果园(图12)进行工作空间试验。该果园为乔砧密植苹果园，树形为自由纺锤形，株行距为2 m×3 m，平均株高约为3.5 m，试验人员肩高为1.41 m，体质量为65 kg。

试验仪器包括：直川电子科技有限公司ZCT 230M型倾角仪，Panasonic公司HG-C1100型激光位移传感器，杰科斯JK-100F系列土壤水分仪，史丹利STHT 36191-23型钢卷尺和李宁AQAP322型秒表等。

4.1.2试验设计

以D-H坐标原点为实际坐标系原点，工作台保持水平，以平台承载质量、横坡坡度及纵坡坡度为影响因素进行工作空间尺寸偏差测量试验，设计三因素三水平试验，如表5所示。

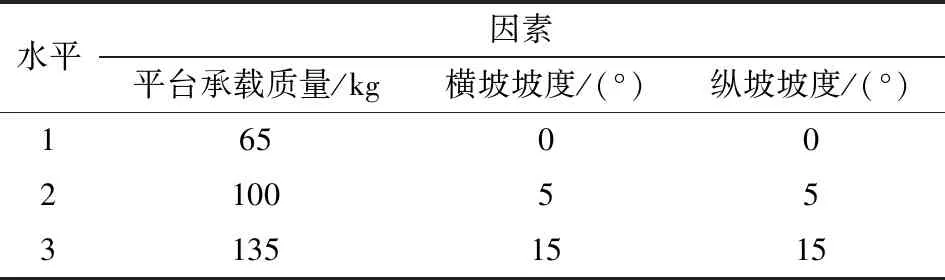
表5 试验因素水平Tab.5 Factors and levels

4.2 试验结果与分析

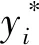
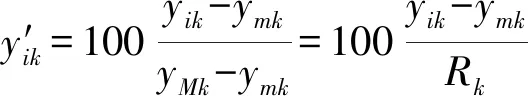
(k=1,2;i=1,2,…,9)

(15)

(16)

式中y′ik——第k项指标第i指标值的评分

yik——第k项指标的第i指标实测值

yMk、ymk——第k项指标最大、最小实测值

Rk——第k项指标的实测值极差

ηk——第k项指标的权重，由表2给出

表6 试验方案与结果Tab.6 Test scheme and result

5 结论

(1)在果园作业平台前期研究基础上，结合农机农艺融合确定了其目标工作空间，采用网格迭代算法求取可达工作空间体积，以工作空间尺寸偏差、工作空间体积和平均可操作度描述可达工作空间性能，分析了平台结构参数杆长、关节角和连杆偏移对可达工作空间性能的影响。

(2)建立了以可达工作空间性能和结构紧凑为目标的优化模型，通过引入各指标比例因子和权重转换为单目标函数，利用遗传算法求解得出最优结构参数为：杆2和杆4的长度分别为988、879 mm，关节1、3的关节角范围分别为[107°,256°]、[-118°,-76°]，关节5、6的连杆偏移最大值分别为720、340 mm。优化后工作空间尺寸偏差分别减小96.09%、95.60%，平均可操作度增加1.43%，表明优化后更接近目标工作空间，且操作更灵活。

(3)进行了不同承载质量、不同坡度下的优化样机实地果园工作空间试验，当平台承载质量65 kg、横坡坡度15°、纵坡坡度15°时，实际工作空间尺寸偏差最大值仅为16.7 mm，较原型减小了93.76%。