曲面轮齿斜置式稻田行间除草装置设计与试验

王金武 马骁驰 唐 汉 王 奇 吴亦鹏 张振江

(1.东北农业大学工程学院， 哈尔滨 150030； 2.南通富来威农业装备有限公司， 南通 158400；3.黑龙江牡丹江农垦向明农业机械制造有限公司， 虎林 226009)

0 引言

机械除草是一项环境友好型杂草防控技术[1]，具有无化学污染[2-4]、可改善土壤物理环境[5]、促进作物生长发育[6-7]、提高水稻产量[8-9]等优点，近年来已被大面积推广使用。水田土壤、旱田土壤特性不同，水田土壤长期浸水，具有含水量高、强度低、粘性大等特点[10]，使水田除草作业性能和作业稳定性较难保证，这也是水田机械除草的重点与难点。因此，高效的机械除草是提高水稻品质和保证水稻安全的基础。

目前，行间机械除草装置按结构形式主要分为鼠笼式和耙齿式。近年来，国内外相关学者对水田除草装置进行了结构优化设计[11-13]和除草机整机轻简化设计[14-15]，而鲜见对除草关键部件结构的创新性设计，并且缺乏关于除草关键部件结构与除草性能间关系的研究。现有除草装置的除草轮多为多个金属板条横置或竖置焊接于除草轮盘，对土壤扰动不足、易黏附土壤和挂草，导致除草作业性能不稳定；通过减小作业幅宽可降低除草轮及其安装架在作业过程中对稻株茎叶和根系的损伤，但导致其有效除草幅宽和除草率均同时下降；除草轮与安装架多为刚性连接，其仿形能力差，无法保证作业性能的稳定。因此，需要开发一种能够高效、稳定的水田行间除草装置。

针对以上问题，本文设计一种被动式曲面轮齿斜置式稻田行间除草装置，通过理论分析确定除草轮盘结构形式和影响作业性能的结构参数及取值范围，通过正交旋转试验与显式动力学仿真确定除草轮盘的最优参数组合，通过田间对比试验验证该装置的作业性能。

1 整体结构与工作原理

1.1 整体结构

曲面轮齿斜置式稻田行间除草装置的结构如图1所示，主要由固定架、压力调节弹簧、支架、除草轮安装架、曲面轮齿除草轮和固定轴承等部件组成。曲面轮齿除草轮是该装置的关键工作部件，由除草轮圆盘和曲面除草轮齿组成，两个除草轮对称斜置布置。张紧弹簧两端挂接在除草轮安装架和支架上。

1.2 工作原理

该装置由插秧机机头提供动力，通过机架挂接在三点悬挂架上，沿插秧机前进方向运动。作业前，根据入土深度要求调节限深滑掌使装置在恒定深度下运行；根据不同水田地况调节仿形机构弹簧挡位，以实现除草装置遇到田间障碍物或水田地况软硬不均时仍可稳定工作，提高作业性能稳定性。作业时，除草轮在插秧机拉力和泥土摩擦力的作用下在行间作业区域内作被动旋转；以特定斜置角度对置安装的两除草轮圆盘使除草轮整体“上宽下窄”，在保证除草幅宽的同时减小除草轮最下方宽度，有效降低对秧苗根系的损伤；除草轮各轮齿偏移角度与除草轮安装斜置角度相同，提高轮齿入土面积，为除草轮被动旋转提供稳定驱动力；各曲面除草轮齿顺次入土、压埋杂草并搅动土壤，随后带动杂草根部与接触泥土翻转并带出泥土层，使杂草漂浮于水面；曲面除草轮齿出土后，附着在其表面的杂草和泥土在所受合力作用下沿轮齿外表面滑脱，避免挂草现象发生，从而去除作业幅宽内生长的杂草，完成稻田行间除草作业。

2 关键部件设计

2.1 曲面轮齿除草轮

2.1.1除草轮轮齿形式确定

除草轮轮齿结构直接影响除草性能，为探究不同轮齿结构对除草装置作业性能的影响，对曲面结构和直面结构除草轮轮齿作业过程进行力学分析。

(1)入土压埋过程

将土壤视为质点(以下简称土壤颗粒)，建立土壤-轮齿力学分析模型。取除草轮轮齿上一土壤颗粒M，对其入土过程进行力学分析。除草轮作业时的前进速度和转速为匀速运动，作业深度保持稳定。如图2所示，以土壤颗粒中心点为原点O，过土壤颗粒作曲面齿切平面，平行于切平面方向为x轴方向，垂直于切平面方向为y轴方向，建立直角坐标系Oxy。土壤颗粒M受力包括：轮齿对土壤的正压力N(曲面轮齿和直面轮齿分别用Nq和Nz表示)、摩擦力f和重力mg。在入土过程中，轮齿对土壤施加的正压力越大，其对杂草压埋强度越高，因此对正压力N进行分析。

以轮齿曲面结构为例，土壤颗粒M受轮齿对土壤正压力为

Nq=mgcosσ1/μ

(1)

式中σ1——入土过程曲面轮齿接触土壤所受重力方向与切平面方向夹角，(°)

μ——土壤与除草轮齿摩擦因数

同理可得

Nz=mgcosσ2/μ

(2)

式中σ2——入土过程直面轮齿接触土壤所受重力方向与切平面方向夹角，(°)

当轮齿刚接触土壤时，σ1=σ2。随着轮齿逐渐入土，σ1<σ2，即Nq>Nz。因此，曲面轮齿对杂草压埋能力优于直面轮齿。

(2)出土脱附过程

取除草轮轮齿上一土壤颗粒Q，对其出土过程进行力学分析。坐标系建立方式与入土过程相同。土壤颗粒Q受力有重力mg、摩擦力f和轮齿对土壤的支持力FN，如图3所示。出土过程中，土壤在轮齿上所受滑脱合力越大，其滑脱效果越好，越不容易发生堵塞现象。因此，对土壤滑脱时所受合力Fh进行分析。

以轮齿曲面结构为例，假设土壤颗粒Q沿除草轮齿表面只进行滑动，无跳动和滚动现象。因此，mgsinσ3可分解为向土壤提供向心力的分力F1和用来平衡支持力FN的支反力F2，其中F1又可分解为土壤牵连运动向心力Fe和切向分力Ft，建立土壤颗粒Q力学平衡方程为

Farn=marn=FN-F2=0

(3)

Fe=mae=mω2rQ=Ft/cosξ

(4)

Fart=mart=Ft+mgcosσ3-μFN

(5)

式中Farn——土壤颗粒Q所受法向力，N

arn——土壤颗粒Q法向相对加速度，m/s2

ae——土壤颗粒Q牵连加速度，m/s2

ω——除草轮转动角速度，rad/s

rQ——土壤颗粒Q与旋转中心间距离，mm

ξ——土壤颗粒Q和旋转中心连线与切平面夹角，(°)

Fart——土壤颗粒Q所受切向力，N

art——土壤颗粒Q切向相对加速度，m/s2

σ3——出土过程曲面轮齿接触土壤所受重力方向与切平面方向夹角，(°)

由式(3)～(5)可得

Fhq=mart=mgcosσ3-μmgsinσ3+mω2rQcosξ+μmω2rQsinξ

(6)

式中Fhq——曲面轮齿上土壤滑脱时所受合力，N

同理可得

Fhz=mart=mgcosσ4-μmgsinσ4+mω2rQcosξ+μmω2rQsinξ

(7)

式中Fhz——直面轮齿上土壤滑脱时所受合力，N

σ4——出土过程直面轮齿接触土壤所受重力方向与切平面方向夹角，(°)

当土壤颗粒开始滑脱时，σ3=σ4。随着土壤颗粒沿除草轮齿滑脱可得σ3<σ4，于是mgcosσ3>mgcosσ4、μmgsinσ3<μmgsinσ4，即Fhq>Fhz。因此，曲面轮齿滑脱能力优于直面轮齿。

综上所述，轮齿曲面结构相比于直面结构在入土过程对杂草压埋能力和在出土过程对土壤滑脱能力均更优，因此选用曲面结构设计除草轮轮齿。

2.1.2除草轮结构参数确定

除草轮回转半径如图4所示。

为防止除草轮圆盘出现缠草现象，除草轮圆盘和轮齿数量需要满足结构要求[16]

2πr≥l

(8)

(9)

其中

R=r+q

(10)

式中r——除草轮圆盘半径，mm

l——杂草高度，mm

R——除草轮回转半径，mm

q——曲面齿作业深度(曲面作业深度等于曲面轮齿投影长度)，mm

i——除草轮轮齿数量

S——相邻齿根弦长，mm

采用以除草轮圆盘为圆心的偏心圆的一段圆弧作为曲面轮齿的曲线，构成轮齿曲面结构，如图5所示。

曲面轮齿曲线的参数方程为

p2-2epsinδ=ρ2-e2

(11)

式中p——曲面曲线上任一点到除草轮圆盘圆心距离，mm

e——曲面曲线的偏心距，mm

δ——曲线上任一点和除草轮圆盘圆心连线与水平方向夹角，(°)

ρ——曲面曲线的曲率半径，mm

综合上述分析，根据东北地区除草时期农艺要求，最佳除草时期为插秧后7～20 d，作业时，泥土深度180～200 mm，返青后控水，泥浆层深度20～50 mm，在插秧后15 d的除草期内水稻秧苗根部深度为80～100 mm，杂草高度一般不超过240 mm[17-18]，杂草根部深度为30～50 mm[19]。综合以上设计要求，经计算，确定除草轮圆盘半径r=60 mm，曲面轮齿投影长度q为40 mm，除草轮轮齿数量i为14，曲率半径ρ取值范围为60～100 mm，偏心距e取值范围为80～120 mm。

2.1.3除草轮斜置角度和轮齿结构确定

除草作业过程中部件使水稻植株伤苗伤根均会影响植株生长和产量[19-20]，为避免上述现象发生，本文设计将除草轮斜置从而保证在有效作业幅宽不变条件下降低对水稻根系的损伤；改变除草轮安装形式，从而避免安装架损伤稻株茎叶和挂草现象发生；将除草圆盘安装斜置角度和曲面轮齿偏移角度均设置为θ，保证除草轮被动转动动力和入土深度稳定性；设计除草轮齿为梯形结构以便于加工，如图6所示。

为避免除草轮在作业过程中出现伤苗伤根现象，应使除草轮最高点幅宽B2不超过两侧秧苗最小间距B1，同时在土壤最低点处幅宽B4小于两根系最小间距B5，因此，则有

(12)

B4=2b1+d≤B5

(13)

式中d——两除草轮齿间距离，mm

b1——除草轮齿齿顶宽，mm

综合上述分析，根据东北地区水稻常规种植要求，种植行距为300 mm。水稻秧苗根系直径为100 mm[15]，通过实际测量除草期茎叶直径为40 mm，设计除草轮最上方幅宽B2为250 mm，理论除草幅宽B3为200 mm，除草轮最下方幅宽B4为185 mm，两除草轮齿间距离d为25 mm。经计算并对数值进行取整，确定除草轮轮齿齿顶宽b1为80 mm、齿底宽b2为15 mm、固装间距c为10 mm，除草圆盘安装斜置角度和曲面轮齿偏移角度θ为10°。

2.2 仿形机构

除草装置作业时需要根据不同地块泥土条件设置除草轮入土压力，使之能够在合理的入土深度下作业，从而保证装置作业性能稳定一致；同时当遇到障碍物时，需要具有越障能力，防止对装置造成破坏。因此，本文设计了单铰链结构的仿形机构，通过调节弹簧伸长量调整除草轮初始入土压力，实现随地仿形功能。

为确定仿形机构各部件结构参数，对仿形机构结构进行简化，建立Oxy平面直角坐标系，如图7所示。

当转臂绕O轴转动角度τ时，转臂ACB转至A′C′B′，由几何关系得

lByB′y=lOBy-lOB′y=l2cosγ-l2cos(γ+τ)=Δh

(14)

lAyA′y=lOAy-lOA′y=l1sinα-l1(α-τ)=Δh′

(15)

(16)

式中lByB′y——By、B′y之间距离，mm

lOBy——O、By之间距离，mm

lOB′y——O、B′y之间距离，mm

lAyA′y——Ay、A′y之间距离，mm

lOAy——O、Ay之间距离，mm

lOA′y——O、A′y之间距离，mm

l1——O、A之间距离，即铰链点左侧转臂长度，mm

l2——O、B之间距离，即除草轮圆心与铰链点之间距离，mm

l3——O、C之间距离，即铰链点右侧转臂长度，mm

l4——C、B之间距离，即除草轮安装架竖直方向长度，mm

γ——OB与竖直方向夹角，(°)

α——转臂与水平方向夹角，(°)

τ——转动后转臂与转动前转臂夹角，(°)

Δh——除草轮遇到障碍物被迫举起高度，mm

Δh′——仿形安全弹簧被迫压缩的长度，mm

当部件在相同地况下作业时，可以认为该部件为刚性结构，弹簧预紧力和弹簧具体参数计算式为

F3cosβl1cosα=F4l3cosα

(17)

F3=kΔh

(18)

(19)

式中F3——弹簧预紧力，N

F4——所受土壤支持力，N

β——弹簧弹力与垂直方向夹角，(°)

k——弹簧刚度系数，N/mm

G——弹性系数，kg/mm2

d1——弹簧线径，mm

Dc——弹簧中心径，mm

Nc——弹簧有效圈数

综合考虑作业地况条件和装置结构配置，确定转臂参数l1=110 mm、l3=50 mm、l4=110 mm，选择弹簧材质为弹簧钢(弹性系数为8 000 kg/mm2)，设定弹簧具体参数为线径d1=2 mm、中心径Dc=18 mm、有效圈数Nc=54，在上述参数条件下，仿形机构的初始下压力调节范围为33.93～96.13 N，能满足作业要求。

3 LS-DYNA虚拟仿真试验

采用显式动力学软件LS-DYNA建立除草轮-水-土壤流固耦合模型，模拟行间除草田间作业环境，以土壤扰动率和耦合应力为评价指标，分析影响除草轮作业性能的主要因素，探寻最优结构参数组合，为后续田间试验奠定基础。

3.1 仿真模型建立

3.1.1除草轮有限元模型

采用Creo3.0软件建立除草轮三维实体模型。为了缩短仿真运算时间，且合理有效地进行仿真模拟与计算，对除草轮模型进行简化处理，材料均采用刚性体定义，去除其工作过程中无关的部件。建模后以.stp格式导入hypermesh软件中，通过六面体网格单元对除草轮模型进行网格划分，生成k文件后导入到LS-DYNA前后处理软件LS-PrePost中。除草轮材料采用MAT_RIGID关键字进行定义，设置其参数为：密度0.007 86 g/mm3，弹性模量2.12×105MPa，泊松比0.288[21]。有限元仿真试验统一使用g-mm-ms单位制。网格划分后除草轮模型如图8所示。

3.1.2水-土壤多物质耦合模型

除草轮在实际作业时的作业对象为水和土壤的耦合物质。为模拟实际田间作业状态，运用LS-DYNA前后处理软件LS-PrePost建模功能进行建模。建立两个长方体实体作为水层模型和土壤模型，将水层模型直接建立在土壤模型上，运用节点重合命令让两个长方体模型进行节点重合，形成由上至下水-土壤两物质耦合模型。根据农艺要求，土壤模型尺寸(长×宽×高)设置为650 mm×300 mm×60 mm，水层模型尺寸(长×宽×高)设置为650 mm×300 mm×30 mm。

土层材料选择LS-DYNA中的MAT_FHWA_SOIL材料，参数取值为：土壤密度0.001 61 g/mm3，土粒密度0.002 73 g/mm3，体积模量5.6 MPa，剪切模量1.9 MPa，黏聚力0.015 5 MPa，内摩擦角15°，含水率40%[22]。其他参数的选取参考MAT147的试验值[23]。

水层材料选择LS-DYNA中的MAT_NULL材料，密度0.001 g/mm3，截止压力-1×10-5MPa。并定义EOS状态方程，用于定义土壤和空气的材料参数。

采用多物质ALE单元算法的SOLID网格单元来定义水层网格和土层网格单元类型。为实现水与土壤在模型中相互混合，采用多物质耦合关键字ALE_MULTI_MATERIAL_GROUP对模型进行设定，设定该关键字命令后，允许一个单元中容纳多种ALE物质材料。为模拟真实的水土模型，对水土耦合模型施加重力条件，运用BOUNDARY_NON_REFLECTING关键字对水土表面进行约束，对土壤底层施加SPC全约束。后通过CONTROL_ALE关键字来对ALE网格光滑化进行激活。虚拟水-土壤复合模型如图9所示。

3.2 除草轮与水-土壤流固耦合仿真过程

根据除草轮实际作业状态及除草农艺要求，设置该装置前进速度为0.8 m/s，入土深度为40 mm。为便于后续除草轮的运动关键字设定，对除草轮设置局部坐标系，并创建向量。除草轮运动可分为匀速直线运动和定轴转动，因此运用DEFINE_CURVE关键字命令对其前进运动速度曲线和旋转运动速度曲线进行定义。通过BOUNDARY_PRESCRIBED_MOTION_RIGID关键字命令调用速度曲线，对除草轮进行前进运动和旋转运动的设置。设置CONSTRAINED_LAGRANGE_IN_SOLID流固耦合关键字命令，将ALE单元体(水-土壤模型)定义为主结构MASTER，将拉格朗日单元体(除草轮模型)定义为从结构SLAVE，设置罚耦合算法进行流固耦合仿真。仿真状态截图如图10所示。

3.3 试验设计

为得到除草轮最优结构参数组合，进行LS-DYNA虚拟仿真试验。根据理论分析结果，确定除草轮曲率半径和偏心距为试验因素，以作业后土壤扰动率和耦合应力为试验指标，采用二因素五水平二次正交旋转组合试验设计安排试验方案，试验因素编码如表1所示。

3.4 试验指标

参照相关文献，以土壤扰动率和耦合应力作为评价指标。

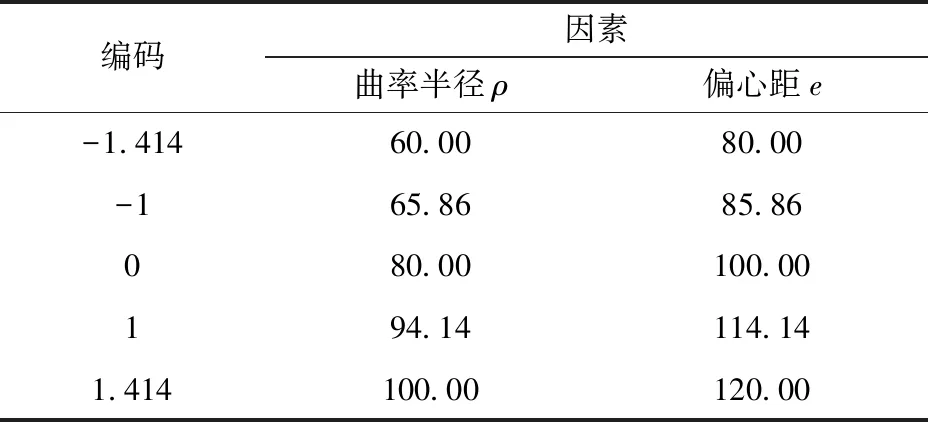
表1 试验因素编码Tab.1 Levels of experimental factors mm

(1)土壤扰动率

土壤扰动率定义为受破坏导致密度下降的土壤单元数与土壤复合模型总单元数的比值，土壤扰动率越大，除草率越高[24]。如图11所示，后处理软件LS-PrePost可对不同时刻密度分布进行测定，并对土壤网格单元密度进行导出。通过将数据导入Excel软件中进行整理，得出总网格单元数与密度下降土壤单元数，可计算出土壤扰动率Sr。

(2)耦合应力

耦合应力为部件与水-土壤模型作用过程中耦合面上所产生的耦合应力平均值，耦合应力越小，部件所受阻力越小，作业能耗越小[25]。如图12所示，后处理软件LS-PrePost对不同时刻应力分布进行测定和导出，并将数据导入Excel软件中进行整理计算。

3.5 试验结果分析与优化

虚拟试验操作值与参数设计值无误差，可根据数据进行结果分析，具体试验方案与结果如表2所示，x1、x2为因素编码值。

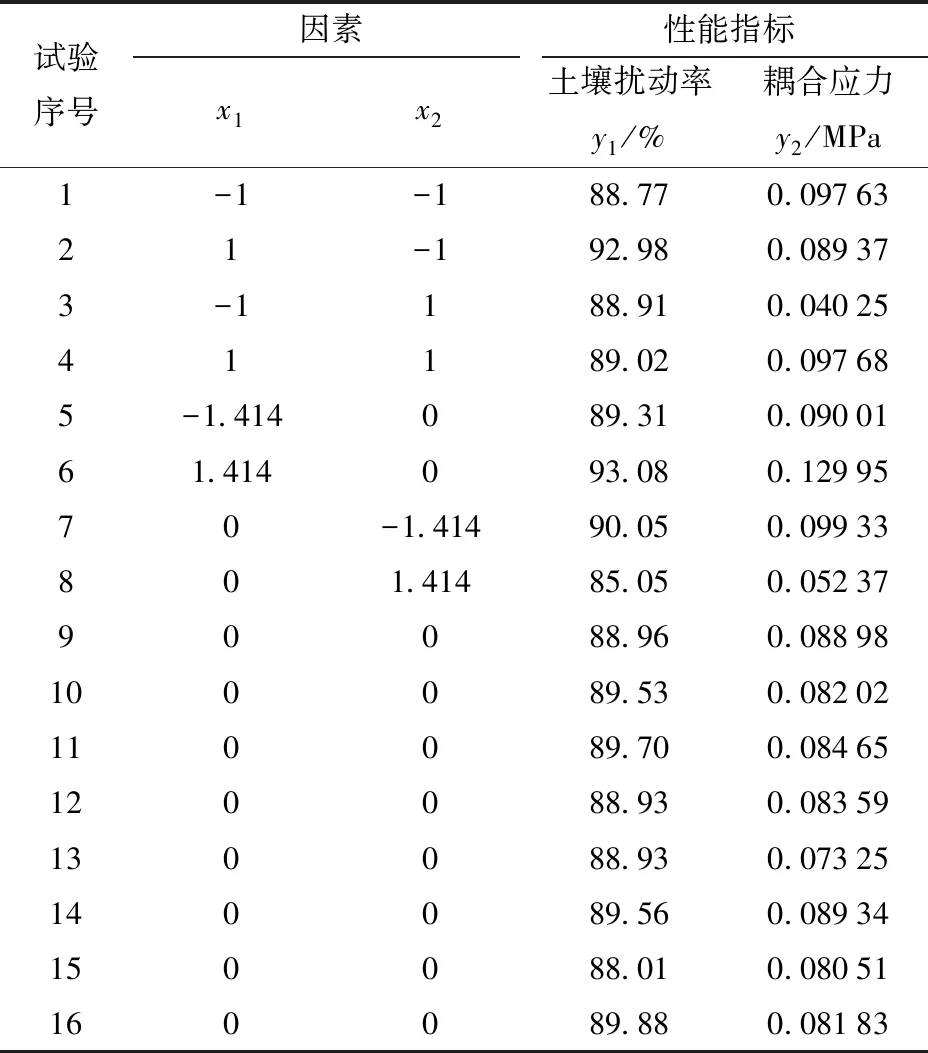
表2 试验方案与结果Tab.2 Schemes and results of tests

通过Design-Expert软件对试验数据进行回归分析和因素方差分析，筛选出影响显著因素，从而得出土壤扰动率y1和耦合应力y2的回归方程

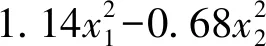
(20)

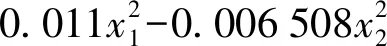
(21)

为直观分析试验因素与指标间关系，运用Design-Expert软件得到响应曲面图，如图13所示。

根据上述回归方程和响应曲面图可知，除草轮曲率半径和偏心距对土壤扰动率存在交互作用，如图13a所示，其中偏心距对土壤扰动率影响比曲率半径显著；当偏心距一定时，土壤扰动率随曲率半径的增加而增加；当曲率半径一定时，土壤扰动率随偏心距的增加而降低。除草轮曲率半径和偏心距对耦合应力存在交互作用，如图13b所示，其中偏心距对耦合应力影响比曲率半径显著；当偏心距一定时，耦合应力随曲率半径增加而增加；当曲率半径一定时，耦合应力随偏心距增加而降低。分析上述影响规律产生的原因可知，除草轮曲率半径增大，增大了除草轮齿作业时与土壤接触面积，从而使土壤扰动率增加，也使耦合应力增加；除草轮的偏心距增大，减小了除草轮齿作业时与土壤接触面积，从而使土壤扰动率降低，也使耦合应力降低。

为得到该行间除草装置最优结构参数组合，对试验因素进行优化设计，遵循提高土壤扰动率、降低耦合应力的原则，采用多目标变量优化方法，结合试验因素边界条件，建立非线性规划参数模型

(22)

基于Design-Expert软件中的多目标参数优化(Optimization)模块对数学模型进行分析求解，从优化结果中选取一组合理参数组合，即当曲率半径为65.86 mm，偏心距为113.27 mm时，行间除草装置作业性能较理想，其土壤扰动率为88.21%，耦合应力为0.045 69 MPa。根据所优化的结果进行虚拟仿真验证，其土壤扰动率为89.63%，耦合应力为0.047 23 MPa，与优化结果基本一致。

4 田间试验

为验证曲面轮齿斜置式行间除草装置在田间作业时工作性能，于2020年6月24日—7月1日在东北农业大学阿城水稻试验示范区进行田间试验。试验期间平均气温20～25℃，无降雨。试验田水层深度为20～30 mm，泥脚深度为160～180 mm。水稻秧苗平均高度为220～250 mm，行距为300 mm，株距为150 mm。杂草主要种类有稗草和野慈菇，平均高度100～140 mm。试验区平均杂草密度为35株/m2。

该装置由南通富来威农业装备有限公司加工试制，曲面轮齿斜置式行间除草装置的结构参数在优化结果基础上进行取整处理：轮齿曲率半径为66.00 mm，偏心距为113.00 mm。该装置通过三点悬挂架与插秧机相连。试验前，调节机器限深装置作业深度为40 mm。试验时控制插秧机前进速度为0.6、0.7、0.8、0.9、1.0 m/s共5个水平，以除草率和伤苗率作为评价指标进行试验，田间试验现场如图14所示。

每次试验结束后，对除草率和伤苗率进行统计。各试验区长度为15 m，设置试验区前后各5 m区域为缓冲区用于机器启停缓冲，以便除草机组稳定通过试验区。

除草率统计方法为在试验区内沿机器前进方向选取5个测试小区，每个测试小区间隔1 m，目的是便于观察作业后杂草数量及状态并方便统计，其测试小区大小为0.2 m(除草装置理论作业幅宽)×1 m。作业前记录每个测试小区内杂草数，作业后统计每个测试小区内剩余杂草数。该试验区除草率即为每个试验小区内已除杂草数之和占每个试验小区内杂草数之和百分比。其中测试小区内杂草根茎被拉断、翻埋、漂起定义为已除杂草；杂草根与泥面相连接，可以继续生长定义为未除杂草[26]。

伤苗率统计方法为在试验前记录试验区两侧总秧苗数，试验后统计出试验区两侧损伤秧苗数。伤苗率即为损伤秧苗数占总秧苗数百分比。试验区内被压折叶片、连根拔起和倒伏定义为损伤秧苗[27]。

每组水平试验重复3次，测试结果取平均值作为试验结果。作业效果如图15所示，相关数据如表3所示。

由表3可知，在相同作业情况下曲面轮齿斜置式行间除草装置的平均除草率为89.66%，平均伤苗率为2.1%，仿真试验中土壤扰动率用来表征除草率，通过除草率田间试验结果与仿真试验结果进行对比可知，更大的土壤扰动导致了更优的除草效果，也验证了仿真试验的可行性。田间试验结果表明，曲面轮齿斜置式行间除草装置除草作业性能良好，作业质量满足水田中耕行间除草农艺要求。

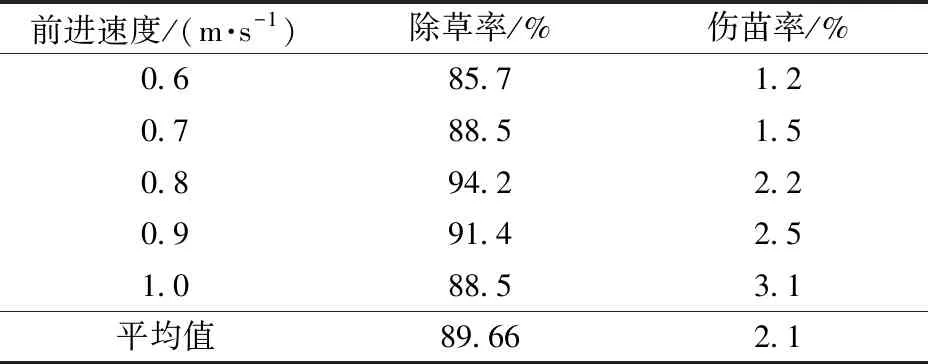
表3 田间试验结果Tab.3 Test results

5 结论

(1)设计了一种曲面轮齿斜置式行间除草装置，该装置能有效清除水田行间杂草，其除草率高、伤苗率低、工作性能稳定，作业质量满足水田中耕行间除草作业要求。

(2)对土壤在轮齿表面上的运动过程进行理论分析，结果表明，曲面轮齿结构除草轮的杂草压埋效果和脱土效果均优于直面轮齿结构的除草轮。通过理论分析和数值计算得出影响作业性能的结构参数为除草轮曲率半径ρ和偏心距e，确定了ρ取值范围为60～100 mm，e取值范围为80～120 mm。

(3)运用显式动力学软件LS-DYNA构建部件与水-土壤流固耦合仿真模型，以除草轮曲率半径和偏心距为试验因素，以土壤扰动率和耦合应力为试验指标，采用虚拟正交试验方法建立了因素与指标间的数学模型，运用多目标变量优化方法建立了优化模型，得出除草轮轮齿最优结构参数组合为曲率半径65.86 mm、偏心距113.27 mm。

(4)田间验证试验表明，在最优结构参数组合下，曲面轮齿斜置式行间除草装置平均除草率为89.66%、平均伤苗率为2.1%，满足农艺要求。