基于裂隙几何特征的岩体渗透率预测

郭忠华

(吕梁学院 矿业工程系，山西 吕梁 033000)

资源开采和工程建设均涉及岩体渗流问题[1-4]。流体在岩体裂隙中快速运移，也会通过周围基质块中微小孔隙相对缓慢地迁移[5]。岩体中存在着大量的孔隙和裂隙，而裂隙介质通常表现出很强的水力复杂性，这些都严重影响到岩体的渗透特性和水流规律[6]。基于岩体渗透率采取合理的防渗措施是防控岩体渗流危害的有效手段，而准确地预测岩体渗透率是预防和消除岩体渗流影响的关键，能够避免突水等灾害造成的经济损失并减少工程建设中过度防渗的经济浪费。

三维模型在描述实际裂隙岩体产状、渗透率张量方面具有突出的优势[7，8]。但是，当裂隙分布较为密集时，对每个裂隙面都进行精细计算是不现实的，因此，此类分析通常简化为二维问题[9，10]。二维平面只是三维岩体的剖切面，无法展现岩体内部裂隙的真实产状，直接使用二维渗透率来近似反映三维渗透率会在大小和方向上出现明显误差[11，12]。但是二维模型能够直接使用地表出露的几何特征，这使得二维模型仍然很有吸引力[13，14]。

目前有很多研究将三维裂隙网络的特征与二维裂隙网络联系起来。周维垣等[15]基于自协调法利用岩体结构勘测面产生的二维网络图形得到三维裂隙网络；冯增朝等[16]从分形理论的角度讨论了三维裂隙面数量分布的分形参数与其二维剖面裂隙迹线数量分布的分形参数间的强相关性。Ebigbo等[17]使用裂隙网络几何参数预测了基于包裹体的有效介质模型渗透率，其中包括球形裂隙的纵横比和基质/裂隙渗透率比值。Lang等[18]提出了使用二维切面渗透率近似表达三维模型渗透率的公式，但是其二维切面需要从其他三维模型中提取因此无法使用相应的二维切面渗透率直接去预测其三维渗透率。Huang等[19]基于二维切面渗透率提出了三维离散裂隙网络的渗透率预测公式，但是其模型并未考虑岩体水力学参数的尺寸效应及岩体基质的渗透性，模型存在一定的局限性。岩体中裂隙分布的随机性往往会导致其水力学参数呈现出明显的尺寸效应，而随着岩体尺寸的增大其岩体等效水力学参数才趋于稳定[20]。此外，虽然基质的渗透能力通常要远小于裂隙渗透能力，但是在砂岩、灰岩、页岩等岩体中考虑基质渗透性时有必要的，而且考虑岩体基质的渗透性时，岩体中的裂隙死端、孤立裂隙及基质-裂隙相互作用都对岩体渗透能力有重要影响[21]。综上，以往研究多是基于裂隙网络模型分析几何产状对二维、三维裂隙网络渗透率的影响，但忽略了岩石基质渗透率和岩体尺寸效应对岩体渗透率的影响，导致预测结果与工程实际存在误差，所以考虑岩体的尺寸效应及岩石基质渗透性对预测三维岩体渗透率是有必要的。

本研究在岩体渗透性表征单元体(REV)尺度上考虑基质渗透性后计算对比了三维模型及其二维剖切面的渗透率，量化了裂隙几何参数及基质渗透率对三维模型等效渗透率的影响，最后建立了三维裂隙岩体渗透率预测模型。

1 概 述

实际岩体中裂隙往往产状各异，仅从地表出露的裂隙特征去推测真实的三维岩体渗流能力会产生明显的误差。但是，很多研究已经表明裂隙几何特征在统计学角度上服从一定的概率分布，如裂隙迹长、倾角等[22]。因此，可以通过现场调查和统计分析，建立结构面几何参数的概率统计模型，进而应用随机模拟法，在计算机上求得表征结构面分布特征的节理网络图像。

在假定了裂隙各个几何参数的先验概率模型后，需要从这些概率分布中进行随机抽样，以得到单个裂隙的具体参数(裂隙面中心点坐标、大小、产状)，将这些参数组合起来就能够生成一个具体裂隙[8，22]。从已知概率分布中的随机抽样可以用Monte-Carlo法模拟实现，Monte-Carlo法已被广泛应用于岩体的裂隙网络模拟[23，24]。在众多三维裂隙模型中，被广泛采用的有Baecher圆盘模型、Veneziano多边形模型等[25]。在本研究中，三维裂隙采用Baecher圆盘模型，不考虑裂隙开度的各向异性，假定裂隙中心点和方向都是均匀分布，裂隙开度为0.1mm。在上述几何假定下，裂隙密度、长度、基质渗透率是能够控制岩体渗透能力的主要参数，详细参数见表1。

表1 裂隙岩体模拟参数

根据相关文献[26，27]可知，岩体的渗透性表征单元体尺寸(REV值)一般为裂隙迹长的3～5倍，因此模拟计算中都取20m×20m×20m的模型进行分析。9个不同裂隙长度及密度的三维岩体几何模型如图1所示：从左到右，裂隙长度从3m增长到5m；从上到下，裂隙密度从0.01条/m3增加到0.1条/m3。从图1可以看出，随着裂隙长度及密度的增加，裂隙网络的连通度逐渐增加。

图1 不同裂隙长度、密度的三维裂隙岩体几何模型

本研究中，认为基质与裂隙都具有渗透性，流体既在岩体裂隙中快速运移，也会相对缓慢地通过周围基质块中微小孔隙迁移。假设基质为各向同性，流动遵循达西定律，基质中连续性方程为：

式中，km为基质的渗透率；Q为基质中的源汇项。使用式(1)，即可在基质中获得可连续微分的压力场。

对于表面光滑的裂隙和流速较低的流体，一般使用立方定律去描述裂隙水的流动：

式中，w为裂隙的宽度；e为裂隙开度；Q为裂隙中的源汇项。在基质和裂隙交界面处压力和流速连续，从而将两种介质中的流动耦合起来。

为了将三维裂隙网络和二维裂隙网络联系起来，在每个三维模型中截取了6个切面形成二维裂隙岩体平面，截取方向平行于流动方向，即平行于x-y平面。截取二维平面的过程如图2(a)所示，施加边界条件如图2(b)所示。三维模型与二维平面边界条件一致，即入、出口两端施加压力边界，其他边界不透水。统计模型出口流量，即可得到岩体等效渗透率：

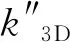
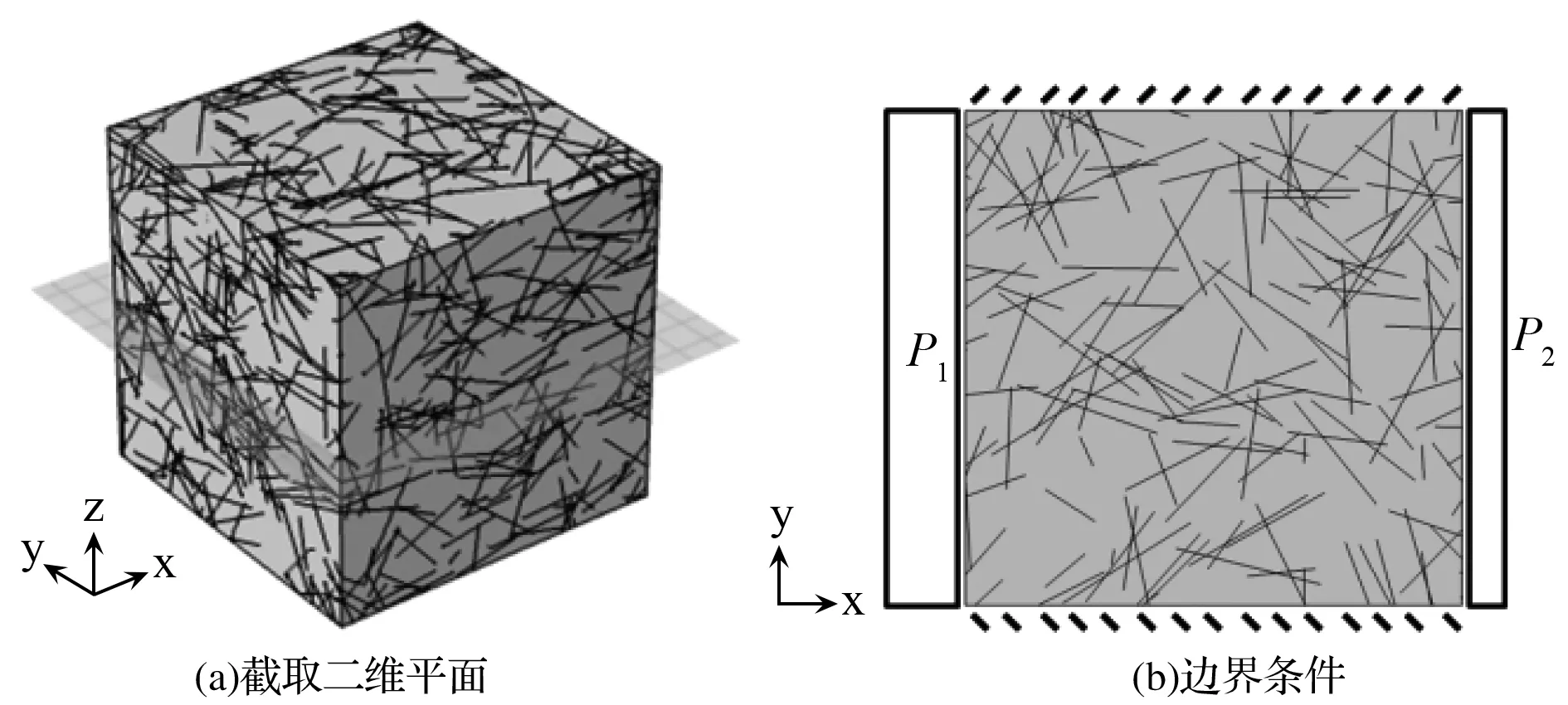
图2 截取二维平面及边界条件

2 计算结果

统计不同裂隙几何参数下的三维裂隙岩体等效渗透率计算结果，分析裂隙长度、裂隙密度、基质渗透率对岩体等效渗透率的影响，并分析了二维、三维模型的差异。

2.1 裂隙长度对岩体等效渗透率的影响

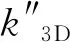
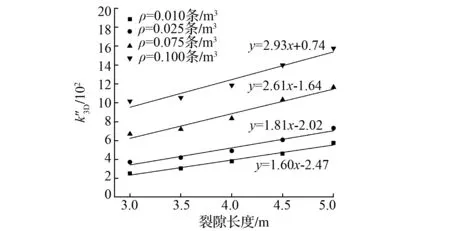
图3 不同裂隙密度下无量纲等效渗透率与裂隙长度的关系

2.2 裂隙密度对岩体等效渗透率的影响

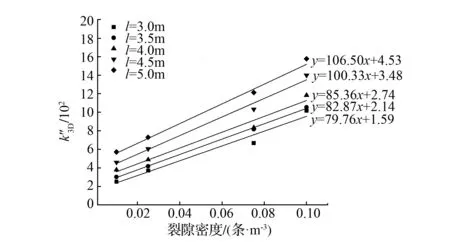
图4 不同裂隙长度下无量纲等效渗透率与裂隙密度的关系

2.3 基质渗透率对岩体等效渗透率的影响

图5 不同裂隙密度下无量纲等效渗透率与基质渗透率的关系

2.4 三维模型与二维平面等效渗透率关系

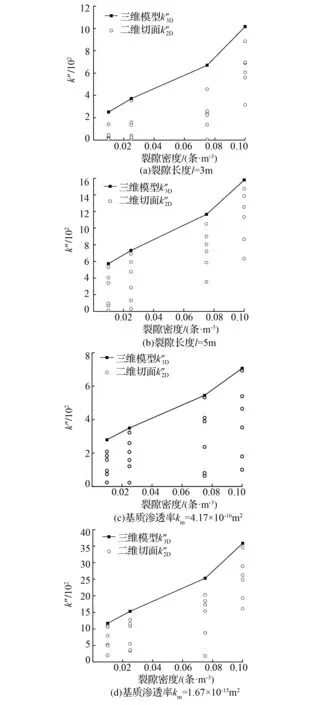
图6 三维模型及其二维切面在不同裂隙长度、基质渗透率下的无量纲等效渗透率

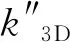
3 三维岩体等效渗透率预测

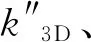
3.40×1015km-2.35

(4)

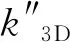
图7 预测值与模拟结果对比

Huang等人[19]为了研究二维切面、三维裂隙岩体渗透率间的联系，计算了18个不同裂隙密度、迹长的裂隙岩体渗透率，也提出了三维裂隙岩体渗透率预测公式，现将式(4)计算结果与之对比，结果如图8所示。由图8可知，三个数据集之间存在较好的一致性。

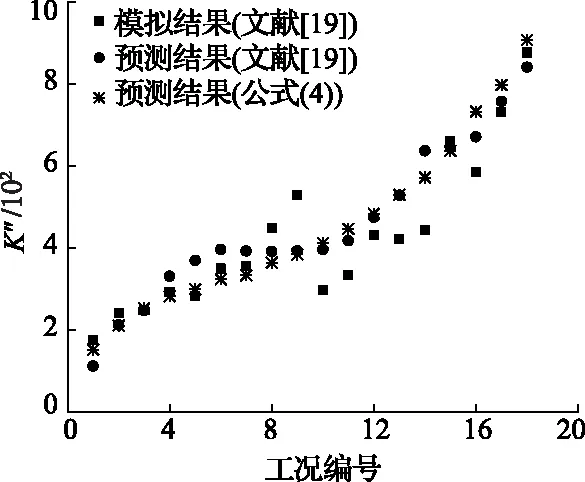
图8 公式(4)预测值与文献[19]模拟结果对比

4 结 论

1)通过对比不同裂隙长度、密度、基质渗透率下的三维岩体等效渗透率，发现在模拟条件下三维岩体等效渗透率与裂隙长度、密度、基质渗透率呈现为线性关系，并分别拟合得到了三维岩体等效渗透率与裂隙长度、密度、基质渗透率的关系式。

2)通过对三维岩体中切面进行渗流计算分析，发现二维切面等效渗透率整体要比三维岩体等效渗透率要小，且差距与数值波动随着裂隙长度、密度、基质渗透率的增长而逐渐减小。