TBM净掘进速率预测模型及多指标评价方法研究

张全太，刘泉声，黄 兴

(1.武汉大学 土木建筑工程学院 岩土与结构工程安全湖北省重点实验室，湖北 武汉 430072；2.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，湖北 武汉 430071；3.盾构及掘进技术国家重点实验室，河南 郑州 450001)

TBM(全断面隧道掘进机)工法具有“安全、施工速度快、环保、成本低”等优点[1]，已成为深埋长大隧(巷)道施工的首选和发展方向。TBM工法在水利、交通领域隧道建设已广泛应用，近年来正在成为我国煤矿井巷掘进的新模式，已成功应用于山西大同塔山煤矿主平硐[2]、神华补连塔煤矿斜井、淮南张集煤矿瓦斯抽采巷等井巷的建设。TBM掘进性能预测在TBM可掘进性评价、施工设计指导和工期规划中具有重要作用，其中净掘进速率(PR)是指TBM一次连续掘进过程中挖掘长度与相对应挖掘时间的比值，可以直观地描述TBM的掘进效率，对于合理规划施工周期和成本估计具有重要作用。因此，开发TBM净掘进速率预测模型在隧(巷)道开挖和设计工作的早期阶段都具有重要意义。

国内外学者基于不同的输入参数和建模方法，已经开发了一些PR预测模型。在国内，温森等[3]基于美国纽约皇后输水隧洞掘进数据和岩体参数，采用Monte Carlo-BP神经网络建立了PR预测模型；王健等[4]以基于RMR的岩体质量评价指标为输入参数，通过统计回归分析方法建立了PR预测模型；闫长斌等[5]以围岩力学参数和岩体指标参数为输入，通过统计回归分析方法建立了TBM净掘进速率预测模型。在国外，美国科罗拉多矿业学院基于室内切割试验数据，采用回归分析方法开发了CSM模型[6]；挪威科技大学基于大量的TBM隧道施工性能数据和地质资料，对岩体参数和机器参数进行回归分析后得到了NTNU模型[7]；Yagiz等基于美国纽约皇后隧道数据，采用了统计回归分析[8]、人工神经网络[9]、粒子群算法[10]等建立了PR预测模型。

国内外学者虽然基于不同的输入参数和建模方法对PR预测进行了研究，但仍然存在一些不足，主要表现在：建模方法单一，无法对比不同方法建立模型的优劣，难以得到最优模型；人工神经网络和机器学习模型超参数的选取依赖人为经验，模型性能优劣随机性较大；基于人工神经网络和机器学习建立的模型算法单一，缺乏与其他算法融合优化。此外，目前在不同模型的多指标综合评价中常用的“排名法”仅能实现定性比较，无法实现更为细致的定量评价。因此，本文基于文献[11]中马来西亚Pahang-Selangor隧洞的样本数据，分别采用统计回归分析、人工神经网络、机器学习方法建立11个PR预测模型，在人工神经网络和机器学习方法中融合贝叶斯算法对模型超参数进行自动优化选取；然后将人工神经网络和机器学习算法与集成学习算法融合建立6个多算法融合的PR预测模型。最后提出一种新的归一多指标模型评价方法(归一法)，同时使用已有的排名法和新提出的归一法对所有模型进行多指标综合评价，根据评价结果对比分析排名法和归一法的效果。研究成果为合理评估TBM隧(巷)道施工周期，预估工程成本提供了理论依据。

1 基于SRA的预测模型

1.1 数据来源

由于TBM掘进速度快，监测环境复杂，岩体参数获取困难、获取数据量有限，而文献[11]公开发表了详细的岩体参数和TBM掘进数据，因此本研究拟基于文献[11]公开发表的马来西亚Pahang-Selangor隧道数据展开研究。收集的数据分为两类：一是从现场测试和TBM设备收集，包括岩石质量指标(Rock Quality Designation，RQD)、岩石质量评级(Rock Mass Rating，RMR)、岩石风化程度(Degree of Rock Weathering，WZ)、TBM推力(Thrust Force，TF)和TBM刀盘转速(Revolutions Per Minute，RPM)；二是实验室测试，包括岩石单轴抗压强度(Uniaxial Compressive Strength，UCS)和巴西劈裂强度(Brazilian Tensile Strength，BTS)。每10m收集一次数据，共计100组数据，其中新鲜岩石53组，轻微风化岩石28组，中度风化岩石19组，数据类型覆盖较全面。在后续建模过程中，新鲜、轻微风化和中度风化岩石分别用1、2和3表示。

1.2 一元线性回归预测模型

对各个变量与PR进行一元回归分析，得到一元线性回归模型，见表1。由表1可知，PR与RQD、UCS、RMR和BTS呈负相关，与WZ、TF和RPM呈正相关，各个变量与PR的相关程度由高到低依次为UCS、TF、BTS、RMR、RQD、RPM和WZ。

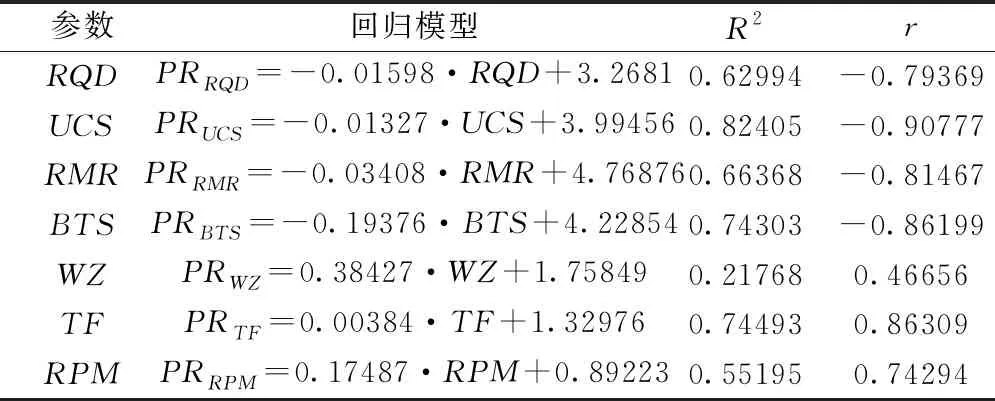
表1 一元线性回归模型

1.3 多元线性回归预测模型

为便于进行多元线性回归分析，对上述7个参数进行线性化处理[12]，即令RQD′=PRRQD、UCS′=PRUCS、RMR′=PRRMR、BTS′=PRBTS、WZ′=PRWZ、TF′=PRTF和RPM′=PRRPM得到线性化后的数据。假设线性化后的各参数与PR的函数关系为：

PRALL=a0+a1·RQD′+a2·UCS′+a3·RMR′+

a4·BTS′+a5·WZ′+a6·TF′+a7·RPM′

(1)

式中，a0、a1、a2、a3、a4、a5、a6、a7为回归系数。

根据式(1)对线性化后的数据进行拟合，得到多元线性回归预测模型为：

PRALL=-0.32849+0.18519·RQD′+0.34488·

UCS′+0.20269·RMR′+0.10743·BTS′-0.20825·

WZ′+0.41776·TF′+0.0883·RPM′

(2)

将表1的线性化变换公式代入式(2)得到多元线性回归预测模型为：

PRALL=3.34332-0.00296·RQD-0.00458·

UCS-0.00691·RMR-0.02082·BTS-0.08002·

WZ+0.00145·TF+0.00363·RPM

(3)

基于式(3)得到的PR预测值与实测值对比分析，如图1所示。多元线性回归模型预测值与实测值的决定系数为0.924，相关系数为0.961，表明该模型具有良好的预测能力。

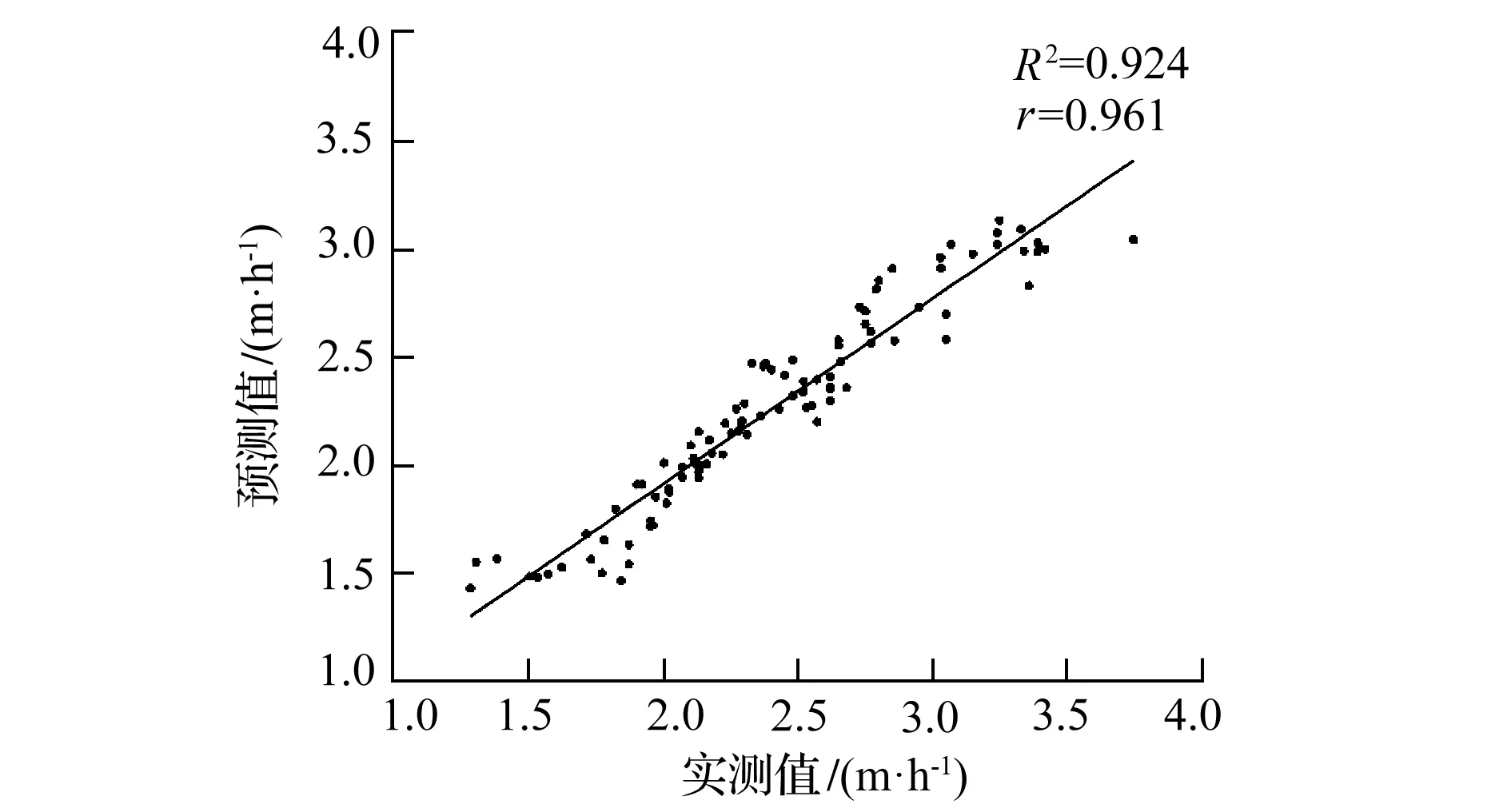
图1 多元线性回归模型预测值与实测值统计分析

2 基于ANN和ML的预测模型

2.1 模型超参数的贝叶斯优化方法

超参数对人工智能和机器学习模型预测性能的优劣具有重要影响，且不少超参数为连续超参数，通过人工试算的方法难以选取合适的值。

目前常用的超参数优化方法有网格搜索法[13]、随机搜索法和贝叶斯优化。网格搜索法对所有的超参数取值组合进行测试，寻找优化的超参数，适用于离散超参数的优化；随机搜索是在给定搜索空间中随机选取超参数组合进行测试，优化得到的结果随机性较强；贝叶斯优化在给定的搜索空间中先随机选择几组超参数进行初始测试，根据测试结果建立超参数组合与优化目标的映射关系，用于指导下一组超参数的选择。每一组超参数测试结束后都会用于修正映射关系，使得到的下一组超参数优化效果更好。因此本文将贝叶斯算法与人工神经网络和机器学习算法融合，优化模型超参数。应当注意的是，模型超参数优化空间的复杂度随优化个数的增加呈指数增加。应当选择对模型性能有重要影响的超参数进行优化，一般不超过三个，避免优化结果陷入局部最小值。

2.2 基于ANN的PR预测模型

ANN是指由大量的处理单元(神经元)互相连接而形成的复杂网络结构[14]，对于复杂的函数关系具有良好的拟合能力。根据Komogorov定理和Hornik存在性定理，含有一个隐含层的神经网络可以精确实现任意连续函数，且隐含层个数增加容易造成模型过拟合。因此本文建立一个三层的ANN模型，输入层包含7个神经元，输出层包含1个神经元。ANN中对模型收敛速度和预测效果影响最大的两个超参数是隐含层神经元个数N和学习率lr，对这两个超参数进行优化选取，隐含层神经元个数优化空间为[5，20]内的整数，学习率的优化空间为(0，1)。优化过程如图2所示，最终取得优化超参数N=17，lr=0.061。基于上述超参数建立ANN模型。

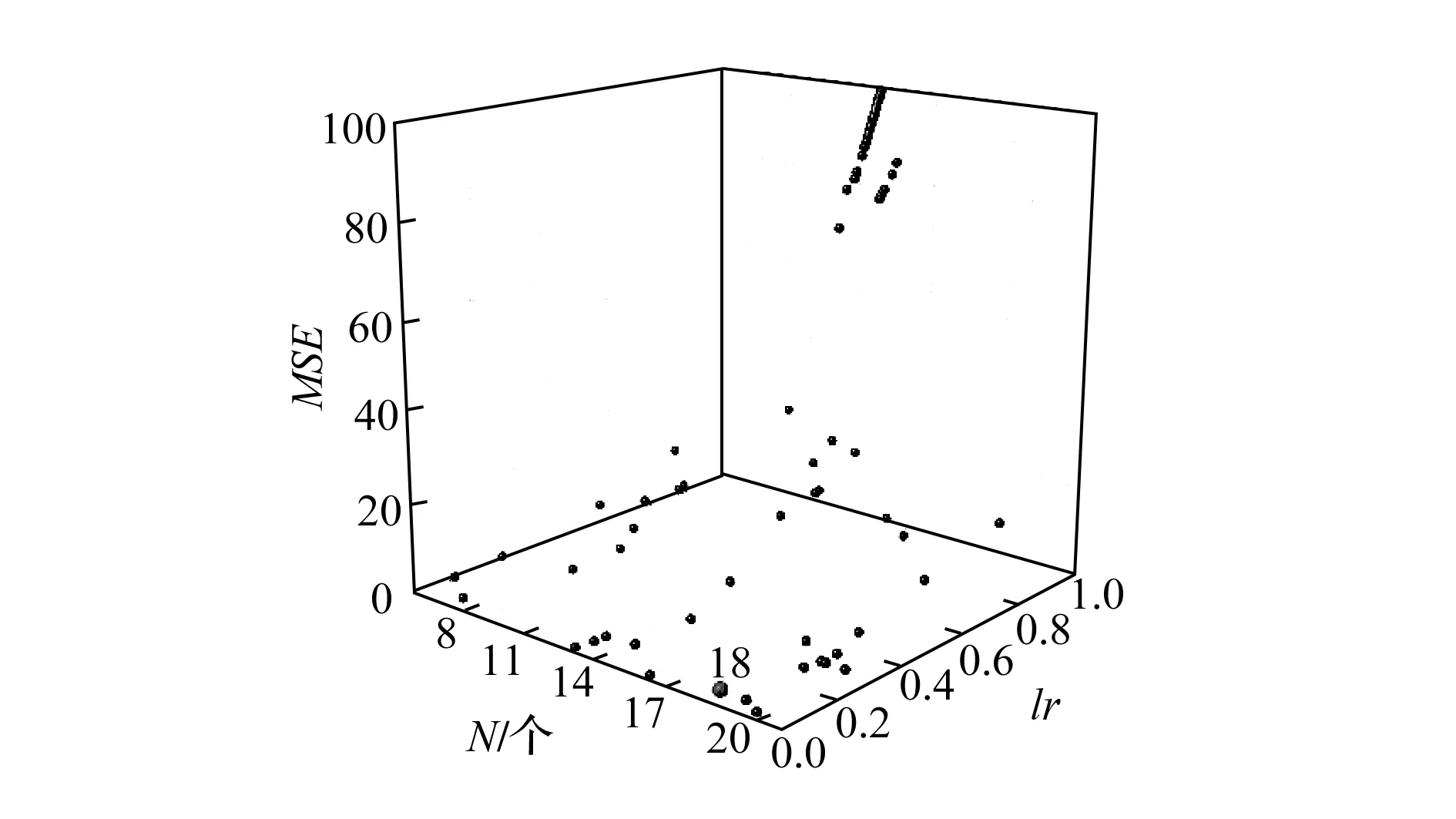
图2 ANN超参数优化过程

2.3 基于ML的预测模型

支持向量回归是在支持向量机中引入核函数用来解决回归问题，该模型可以解决样本数量较少时的机器学习问题，且对于非线性、高维度问题具有较好的拟合能力[15]。分类与回归树既可用于分类问题，也可用于回归问题[16]，在每个节点通过一个特征的选择进行分类或回归，计算复杂度较低，对中间缺失值不敏感，且模型的可解释性较强。

支持向量回归中不敏感损失系数ε决定回归函数对样本数据的不敏感区域的宽度；惩罚系数C反映了算法对超出ε的样本数据的惩罚程度，其值影响模型的复杂性和稳定性。对上述两个超参数进行优化选取，优化空间均为(0，1)。优化过程如图3所示，最终取得优化超参数C=0.543，ε=0.278。基于上述超参数建立SVR模型。

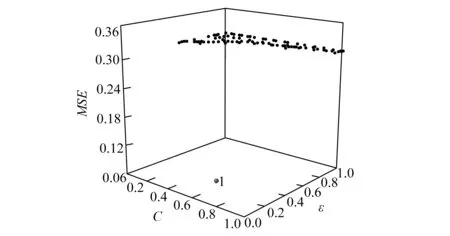
图3 SVR超参数优化过程

分类与回归树中树的最大深度max_depth对模型的复杂程度和预测精度具有重要影响，对该参数进行优化，优化空间为[5，20]内的整数。优化过程如图4所示，最终取得优化超参数max_depth=8。基于上述超参数建立CART模型。

图4 CART超参数优化过程

2.4 多算法融合模型

Bagging(套袋算法)通过平均的思想改善了模型的泛化误差，使预测结果出现较大误差的概率降低。该算法以有放回的方法从样本集中随机抽取一定数量的样本组成子训练集，用k个子训练集分别训练得到k个弱学习器，各个弱学习器独立预测，按一定权重将各个弱学习器预测结果加权求和得到最终的预测结果。AdaBoost(自适应提升算法)通过在迭代训练过程中重点学习预测误差较大的样本以提高预测精度。该算法在训练过程中对于预测误差较大的样本赋予更大的权重，使其在下一次训练时被弱学习器给予更多关注，提高该样本的预测准确率，最终训练得到多个弱学习器，按一定权重将各个弱学习器预测结果加权求和得到最终的预测结果。

将上述的套袋算法和自适应提升算法，分别与ANN、SVR和CART算法融合，建立Bag-ANN、Bag-SVR、Bag-CART、Ada-ANN、Ada-SVR和Ada-CART多算法融合模型，融合模型中弱学习器个数均设为10，ANN、SVR和CART的超参数均采用2.2和2.3节融合了贝叶斯算法得到的优化超参数。

3 预测模型的多指标综合评价及对比分析

3.1 预测模型测试及多指标综合评价

本文的样本集包含100个样本，在ANN和ML模型中为保证训练和测试样本集不同，且训练集具有足够的训练样本，每次将99个样本设为训练集，剩余1个样本设为测试集，循环100次，并计算各个模型的评价指标均方误差(Mean Square Error，MSE)、平均绝对误差(Mean Absolute Error，MAE)、平均绝对百分误差(Mean Absolute Percentage Error，MAPE)、决定系数R2和相关系数r。

对于一个模型，R2和r越接近1，MSE、MAE和MAPE越小说明模型预测能力越好，不同指标评价模型预测能力的倾向不一致(倾向性一致是指模型预测能力越好，评价指标越大的倾向)，因此本文对MSE、MAE和MAPE做如下变换：

回归模型中不同评价指标的侧重方面不同，单一指标对不同模型的评价缺乏全面性，因此需要对不同模型进行多指标综合评价。Zorlu等[17]学者于2008年提出的排名法是目前常用的多指标综合评价方法，其流程为：①对M个模型同一评价指标i分别进行排名；②将同一模型的m个不同评价指标排名相加作为该模型的多指标评价排名，如图5所示。基于排名法得到各个模型的评价结果见表2。

图5 排名法

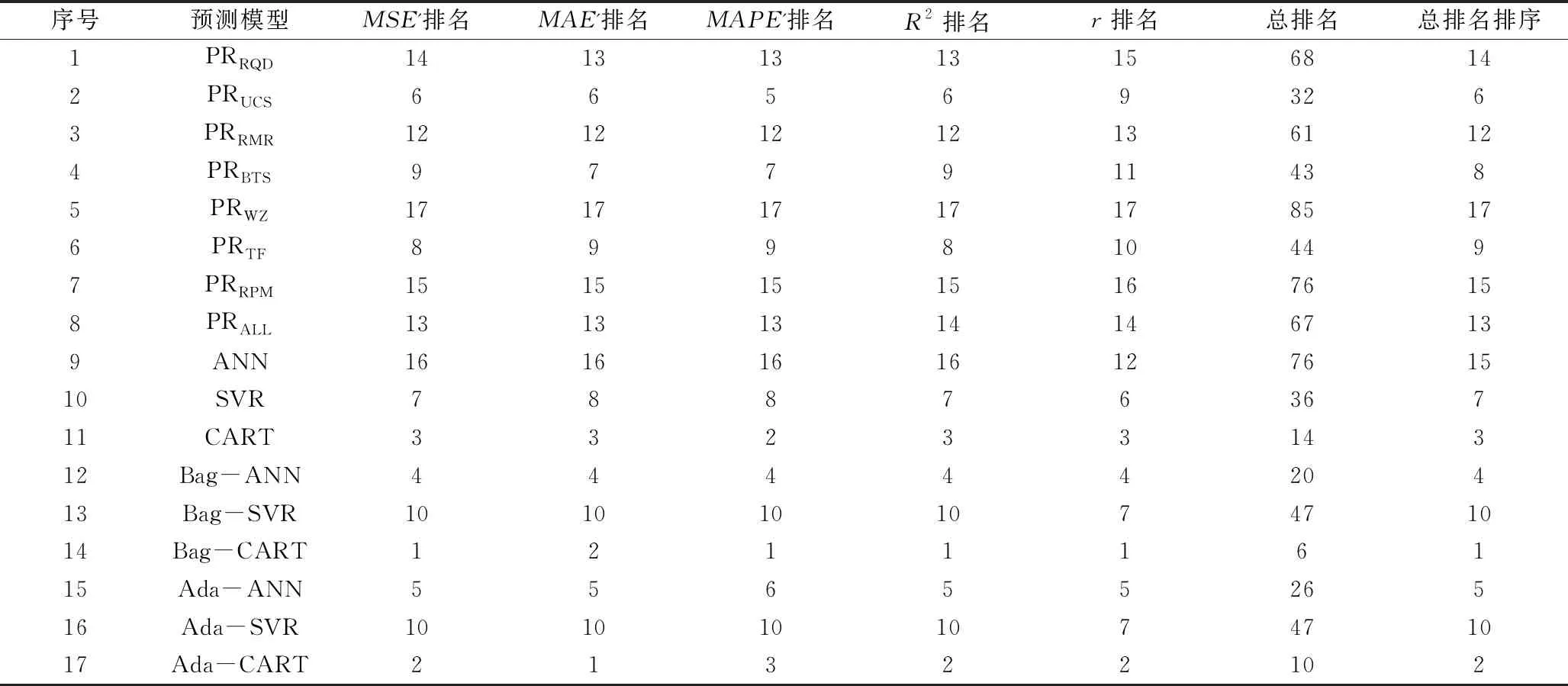
表2 排名法评价结果

3.2 新型归一多指标模型评价方法

对于排名法，如果模型1的A、B指标比模型2的A、B指标好，但相差不大，而模型2的C指标比模型1的C指标好，且相差较大，排名法的结果为模型1优于模型2。但实际情况，更倾向于模型2优于模型1。造成上述问题的原因在于排名法仅能考虑同一评价指标的相对大小关系，忽略了同一评价指标差值大小对模型评价的影响，因此容易造成模型评价不准确。

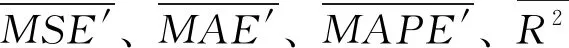
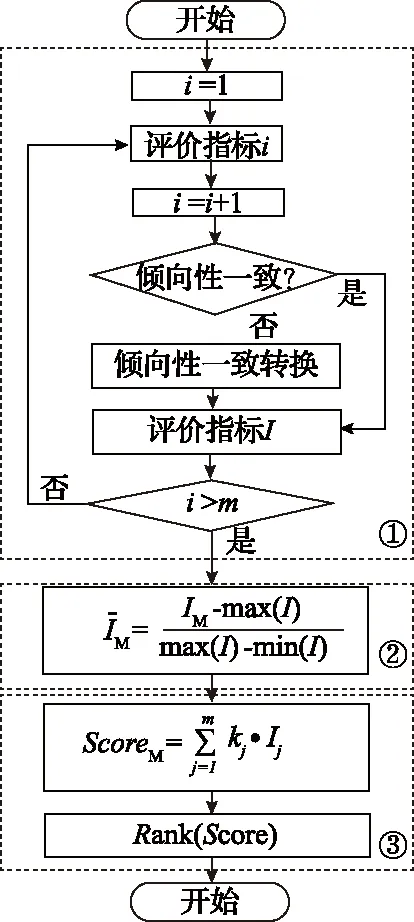
图6 归一法

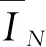
归一法得到各个模型的评价结果见表3。对比表2和表3可以发现，两种方法对各个模型的评价排名基本一致，表明本文提出的归一法是合理的。排名法评价结果(表2)中模型13和16排名均为10，模型7和9排名均为15，表明排名法对于性能差别不大的模型无法精确评价；而归一法评价结果(表3)中模型13排名为10，模型16排名为11，模型7排名为15，模型9排名16，表明归一法相较于排名法对于性能差别不大的模型也可以精确识别。归一法优于排名法的原因主要在于归一法不仅考虑了不同模型同一评价指标的相对大小关系，同时也考虑了同一评价指标差值大小对模型评价的影响，而排名法仅能考虑前者。因此，归一法相较于排名法对各个模型的多指标综合评价更加准确细致。

表3 归一法评价结果

3.3 PR预测模型对比分析

从整体来看，基于SRA建立的模型具有明确的函数关系，属于“白箱子”模型，易于分析各个变量对PR的影响，模型可解释性较强；基于ANN、ML和多算法融合建立的模型属于“黑箱子”模型，可解释性较差，但预测精度较高。

基于SRA建立的模型中一元回归模型的预测能力均较低，多元回归模型比基于RQD、WZ、RPM建立的一元回归模型预测能力好，比基于UCS、RMR、BTS、TF建立的一元回归模型预测能力差。一元线性回归模型形式简单，应用要求低，适用于仅获取了个别参数而又需要对PR进行预测评估的情况，但对于参数的准确获取要求较高，否则容易造成较大误差；多元回归预测模型需要的参数较多，但预测准确性及对单个变量测量的容错性均较高。

基于ANN、ML和多算法融合建立的模型中多算法融合对于ANN和CART模型预测能力均有提升，且对ANN模型预测能力提升明显，表明多算法融合相较于单一算法具有明显优势，在应用人工智能方法解决土木工程中的问题时应注重结合不同算法的优势，提高应用效果。由表2及表3可知，预测性能最好的模型为Bag-CART，其次是Ada-CART，第三是CART，表明本文建立的17个模型中，CART模型和基于CART的多算法融合模型最适合于PR预测。

基于CART模型对7个输入参数的重要性进行了打分和排序，将结果和2.2节输入参数相关性排序列于表4。可见，基于统计回归分析方法和基于机器学习方法对输入参数的重要性排序基本一致。

表4 CART模型输入参数重要性打分及排序

4 结 论

基于马来西亚Pahang-Selangor隧洞100组岩体和TBM掘进参数，采用SRA、ANN、ML和多算法融合方法建立了17个PR预测模型，并提出了一种新的归一多指标综合评价方法用于选择最优模型，主要得到以下结论：

1)TBM净掘进速率一元回归模型预测能力由高到低依次为PRUCS、PRTF、PRBTS、PRRMR、PRRQD、PRRPM和PRWZ，但从整体来看，一元回归模型的预测能力均较低；多元回归模型比基于RQD、WZ、RPM建立的一元回归模型预测能力好，比基于UCS、RMR、BTS、TF建立的一元回归模型预测能力差。

2)多算法融合对于ANN和CART模型预测能力均有提升，且对ANN模型预测能力提升较为明显，但多算法融合也导致SVR模型预测能力略微降低；在本文建立的17个模型中，CART模型和多算法融合模型Bag-CART和Ada-CART的预测能力更好，更适用于PR预测。

3)本文提出的归一法通过“评价指标倾向一致性转换、归一化、求和、排序”等步骤实现了多模型定量地多指标综合评价，与Zorlu等提出的排名法相比，不仅考虑了不同模型同一评价指标的相对大小关系，也考虑了同一评价指标差值大小对模型评价的影响。

4)本文建立的净掘进速率(PR)预测模型对于TBM掘进性能预测、合理评估TBM隧(巷)道施工周期、预估工程成本具有重要的借鉴和指导意义；提出的归一法实现了模型多指标综合评价从定性分析到定量分析，对于准确细致识别不同模型的预测性能具有重要意义。