基于阻抗网络模型的多变流器直流微电网小扰动稳定性分析

刘镇湘，赵晋斌，曾志伟，屈克庆，毛 玲

（上海电力大学 电气工程学院，上海200090）

0 引言

直流微电网以其可靠性高、变换环节少、损耗低且不需要对电压的相位和频率进行跟踪等优点，将成为未来家庭、直流建筑、数据中心、通信基站和现代电力电子负荷的主要供电架构［1-2］。通常可以采用主从控制或对等控制策略来维持直流微电网母线电压恒定［3］。但随着大规模变流器的接入，变流器间交互耦合以及恒功率负荷（CPL）的负电阻特性、功率的双向流动等，可能会导致多变流器直流微电网MCDCM（Multi-Converter DC Microgrid）出现稳定性问题或动态性能恶化等情况［2，4］。合理有效地建立系统小信号阻抗网络模型INM（Impedance Net⁃work Model）以及进行稳定性预判，并进一步分析动态稳定性具有重要意义。

对于系统小信号稳定性问题，主要有基于状态空间数学模型的特征值分析法［5-8］和基于阻抗特性的阻抗匹配法［9-10］等。基于状态空间数学模型的特征值分析法利用系统理论建立的模型更精确，但在多变流器系统中模型十分复杂［6］。与之相比，基于阻抗特性的阻抗匹配法是一种系统的外特性描述，其广泛应用于分析交直流微电网中子系统之间的耦合稳定性问题［9］。

文献［10-14］论述基于小环增益的Nyquist 曲线稳定性分析，如Middlebrook、GMPM（Gain Margin and Phase Margin）、OA（Opposing Argument）、MP（Maxi⁃mum Peak）、ESACC（Energy Source Analysis Con⁃sortium Criterion）、RESC（Root Exponential Stability Criterion）、T-SI（Three-Step Impedance）等稳定性判据。上述判据均是通过设定不同的稳定裕度和禁止区，基于阻抗比对直流微电网进行小信号稳定性分析，这类判据的缺点是规定了功率的流向（电源端输出功率，负荷端吸收功率），但在实际的直流微电网中，有些微源如储能（ES）变换器既可以作为电源运行也可以作为负荷运行，这导致传统阻抗比判据并不适用于多源与多负荷组成的系统［15］。

为了获得较为合理的稳定性分析方法，文献［16］基于阻抗的分析方法对直流微电网的变换器进行分类，并考虑功率流向分析系统稳定性，但没有考虑线路阻抗网络的影响。文献［17］定义基于阻抗规范的分布式电源系统稳定性判据，但该判据仅适用于多源串联、多负荷、功率控制源组成的系统，本质上还是单源与多荷系统。文献［18］基于特征值分析法对少量换流器间的参数配合和源网荷间的交互作用进行研究，但其难以适用于大规模变流器接入的直流微电网系统。

为了克服上述局限性，本文在多变流器馈入的直流微电网系统中计及线路阻抗网络的影响，通过推导其等效负反馈模型，提出一种基于阻抗网络模型的开环传递函数分析方法来研究系统小扰动稳定性问题。本文首先将阻抗网络的概念推广到MCDCM，从而获得系统的阻抗网络模型；然后，为了将阻抗网络模型应用于系统的稳定性判别与设计，推导出对应的等价开环函数，并给出相应的稳定性一般设计流程；最后，通过频域和时域分析证明所提方法在进行MCDCM稳定性的判别与设计时具有较好的优势。

1 直流微电网的阻抗网络模型

1.1 直流微电网拓扑结构

本文主要讨论新能源多馈入条件下的直流微电网系统的小扰动稳定性问题，图1 给出了适用于家庭或楼宇的低压直流微电网的典型结构。

图1 MCDCM典型结构Fig.1 Typical structure of MCDCM

本质上而言，直流微电网在实际应用场景中可以看作是等效源-输电网络-负荷系统，包括直流电压控制单元、输电线路网络和功率控制单元。借鉴文献［16］重塑每个源和负荷的端口特性的思路，将MCDCM 归类为对应的广义电压源（GVS）、无源网络和广义电流源（GCS）。值得注意的是，GVS或GCS是直流微电网的一个子系统，可以是线性负荷、线性源、非线性负荷或变换器控制源等。本文考虑如图2 所示的直流微电网系统，其包含m个GVS 子 系 统、n个GCS 子 系 统。图 中，Usi、Isi(i=1，2，…，m)分别为子系统GVS_i馈入端口电压、电流；Uoj、Ioj(j= 1，2，…，n)分别为子系统GCS_j馈入端口电压、电流；Zsi、Zoj为无源网络线路阻抗。该系统无源网络是由无源阻抗形成的，通过一定的网络拓扑连接系统中的所有源-荷节点，GVS子系统作为输入有源节点，GCS子系统作为输出有源节点。

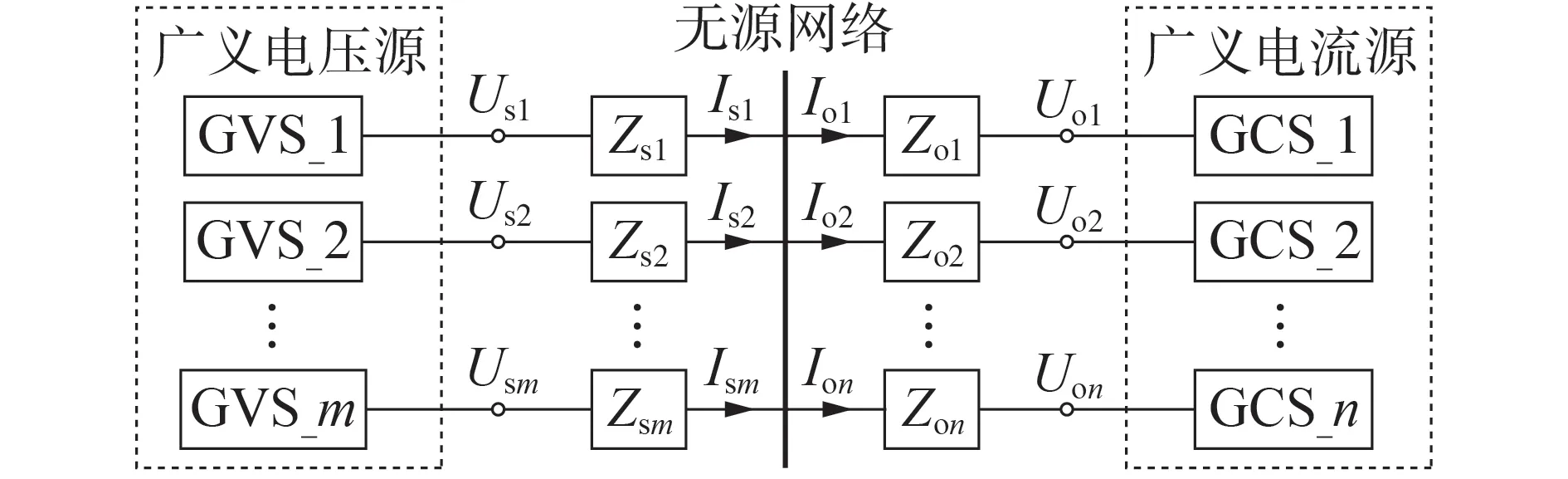
图2 MCDCM等效模型Fig.2 Equivalent model of MCDCM

文献［18］指出：在线性化分析中，MCDCM 的GVS 子系统可采用电压源串联阻抗矩阵的Thevenin等效模型，该模型可用方程式（1）表示；GCS 子系统可采用电流源并联导纳矩阵的Norton 等效模型，该模型可用方程式（2）表示。

其中，Zs为阻抗矩阵；Us、Is分别为GVS子系统馈入端口电压和馈入电流（定义流入直流母线为电流参考正方向）；Yo为导纳矩阵；Uo、Io分别为GCS 子系统端口电压和端口电流（定义流出直流母线为电流参考正方向）。输电线路网络往往建成RL或RLC阻抗模型。

1.2 阻抗网络模型的推导

根据前文定义，GVS 馈入端口与GCS 端口的电压、电流可由矩阵方程线性表示：

其中，G为多端口无源网络的反混合参数矩阵，具体推导过程见附录A。

联立式（3）和式（4）可推导出：

图3 MCDCM的阻抗网络负反馈模型Fig.3 Negative feedback model based on INM for MCDCM

故以LG为开环函数的负反馈模型与图3 所示的系统有相同的稳定性。本文定义MCDCM 阻抗网络模型的开环函数T为：

因此，可以通过研究特征方程det（Im+n+T）来分析每个有源节点的稳定性，其中Im+n为m+n维的单位阵。但特征方程分析较为复杂，文献［19］指出可基于控制硬件，采用考虑频率耦合的阻抗测量方法进行频域扫描分析，该方法可解决阻抗理论建模中的“灰箱化”问题，且无需求得矩阵T的具体解析表达式，因此采用广义Nyquist 判据（GNC）分析系统稳定性较为简便。

2 MCDCM的稳定性分析

2.1 阻抗网络模型开环函数的极点分布

阻抗网络模型开环函数T的极点表示GVS（GCS）子系统的开环极点，在进行频域设计时，通常要求开环函数不存在右半平面（RHP）极点。由式（6）可得：

其中，Zsi为GVS 子系统中第i个端口的输出阻抗；Yoj为GCS子系统中第j个端口的输入导纳。

当GVS 子系统由理想电流源加载时，其输出电压将被设计为稳定，当GCS 子系统由理想电压源供电时，其输入电流将被设计为稳定，因此，在频域分析时，Zsi和Yoj可以被认为是稳定的，即不存在RHP极点。根据无源系统理论［20］可知G中也不存在RHP极点。

通过上述讨论可知，阻抗网络模型的开环函数T不存在RHP极点。

2.2 基于阻抗网络模型的稳定性判据

根据2.1节中的分析可知，阻抗网络模型负反馈系统的开环函数是稳定的。根据多变量频域理论，采用特征值轨迹来分析负反馈模型的稳定性，具体表述如下。

广义Nyquist 判据：如图3 所示的负反馈系统是稳定的，当且仅当T的特征值轨迹包围临界点（-1，0）的逆时针圈数N+等于其包围临界点（-1，0）的顺时针圈数N-时，MCDCM 在小扰动下是稳定的。针对该判据，较理想的情形是N+=N-=0，此时特征值轨迹在几何上不包围（-1，0）。存在T中含有RHP 零点时N+=N-≠0 的情形，但该情形在工程上较为少见，因此可认为N+=N-=0时MCDCM是稳定的。

2.3 直流微电网系统级稳定性分析流程

式（6）表明，在MCDCM 的稳定性分析中，相比于整个系统，显然设计GVS（GCS）子系统的稳定性更容易，因此本文利用阻抗网络模型，将MCDCM 的稳定性设计总结为一程序化流程，如图4所示。

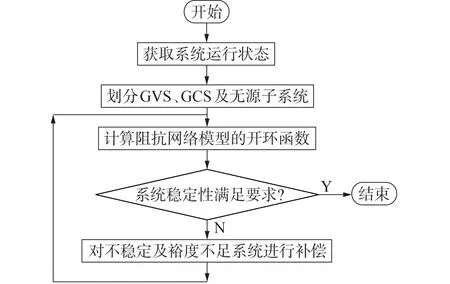
图4 MCDCM的稳定性设计流程Fig.4 Flowchart of stability design of MCDCM

在设计流程中，首先将系统划分为GVS、GCS 及无源子系统，进而计算本文所提阻抗网络模型的开环函数，并利用其判定结果指导各子系统的参数设计，确保MCDCM 的稳定性。若需定量判断系统的稳定程度，可采用基于禁止域的广义Nyquist 判据来研究系统的稳定性。

3 算例研究

建立由光伏（PV）、储能及CPL 构成的MCDCM，如图5 所示。图中，光伏模块通过Boost 变换器接入直流母线；储能模块通过DC／DC 双向变换器接入直流母线；阻性负荷通过Buck 变换器与直流母线相连；GVS 子系统中4 个微源端口变换器均采用电压电流双闭环控制，同时引入下垂控制策略；直流母线电压Ubus=400 V，各变换器开关频率为10 kHz。算例模型中的控制系统和控制参数参考文献［15］以及附录B。

图5 MCDCM算例结构图Fig.5 Structural diagram of MCDCM example

本节算例讨论GVS 下垂系数及负荷功率变化［3］对MCDCM 稳定性的影响，以此验证本文所提稳定性判定方法的正确性。

3.1 下垂系数对MCDCM稳定性的影响

设置系统运行于不同工况，其对应的下垂系数如表1所示。

表1 不同工况下的下垂系数整定Table 1 Droop coefficient setting under different working conditions

图6为下垂系数变化时，MCDCM 的广义Nyquist轨迹和直流母线电压的瞬时值波形。初始运行于工况1下，系统稳定，通过改变下垂系数，在t11=0.4 s时切换至工况2，在t12=0.6 s时切换至工况3。根据广义Nyquist 判据理论，广义Nyquist 曲线不包围临界点（-1，0），这表明系统在3种工况下都处于稳定状态。

由图6（a）可知，当下垂系数减小时，特征根轨迹存在远离临界点（-1，0）的趋势，因此，系统由工况1到工况3 存在的失稳风险增大，整体稳定裕度下降。由图6（b）也可知，在工况1下系统能稳定运行，切换至工况2和工况3时，由于下垂系数在控制侧呈阻尼性质，增加下垂系数使母线电压振幅降低，但加剧了母线电压偏离额定值的程度，系统运行条件恶化，该结果与频域分析一致。

3.2 负荷功率变化对MCDCM稳定性的影响

3.2.1 负荷功率增加情形

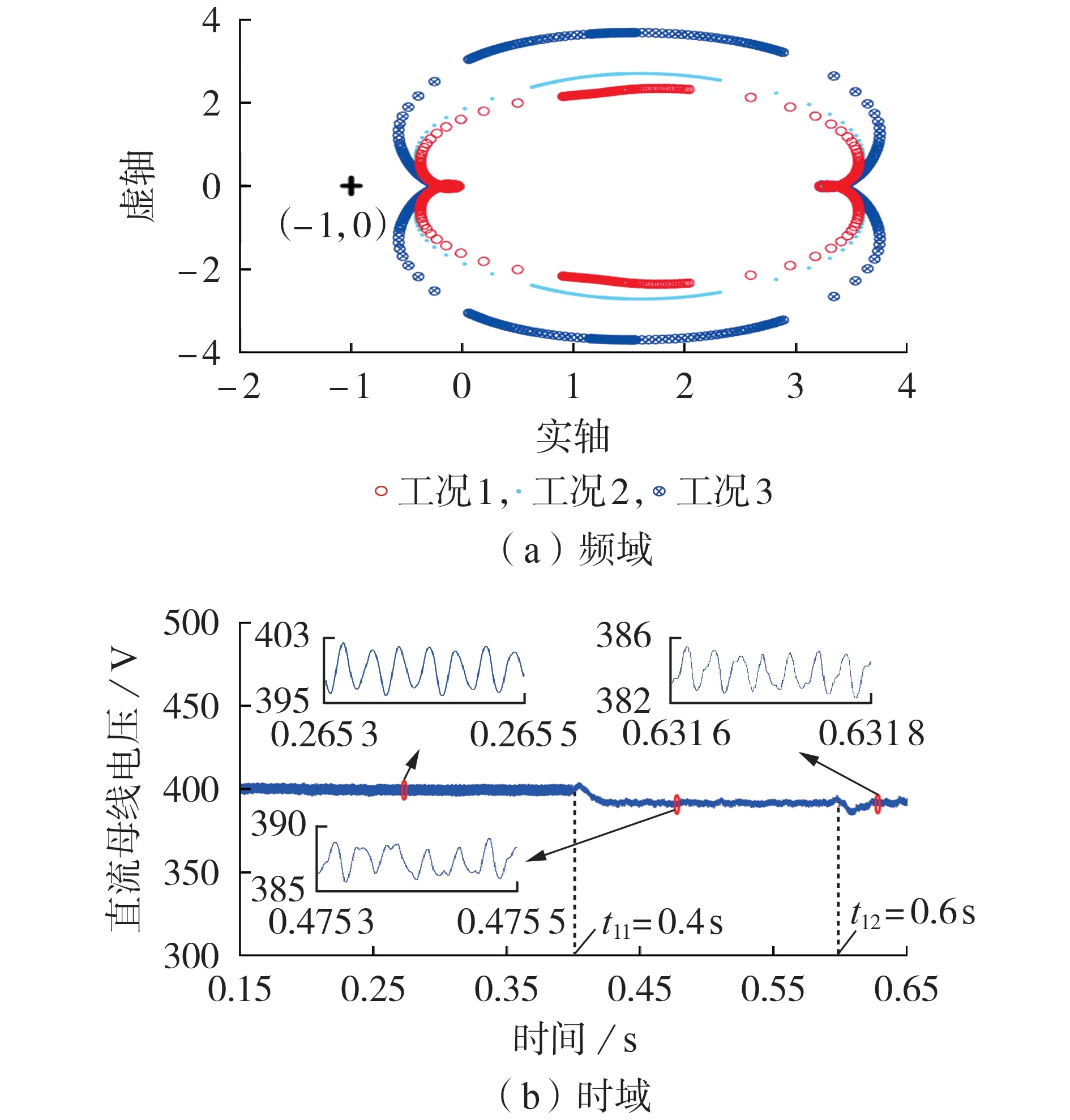
图6 不同工况下MCDCM的稳定性分析结果Fig.6 Analysis results of MCDCM stability under different working conditions

图7 为负荷功率增加时MCDCM 的广义Nyquist轨迹和直流母线电压的瞬时值波形。初始状态下CPL的功率为PCPL=24.0 kW，系统稳定。

图7 负荷功率增加时MCDCM的稳定性分析结果Fig.7 Analysis results of MCDCM stability when load power increases

由图7（a）可知，当负荷功率增加至48.5 kW 时，MCDCM 的广义Nyquist 曲线在复平面中存在左移趋势，这表明系统存在更高的失稳风险，稳定裕度降低。当负荷功率增加至100.5 kW 时，广义Nyquist曲线包围临界点（-1，0），系统不稳定。因此，本文所提方法可对MCDCM的失稳做出预判。

在时域内也存在相同的结论，由图7（b）可知，在t21=0.35 s 时，负荷功率跃升至48.5 kW，直流母线电压经暂降后恢复至额定电压水平。分析t21前后母线电压振幅知，系统的稳定裕度明显下降，母线电压波动更为剧烈，这表明系统失稳风险增加。在t22=0.55 s 时，负荷功率跃升至100.5 kW，系统突破临界稳定点，母线电压始于周期性振荡，终止于非线性发散振荡。综上可知，时域与频域分析结果一致。

3.2.2 负荷功率减少情形

图8 为负荷功率减少时MCDCM 的广义Nyquist轨迹和直流母线电压的瞬时值波形。初始状态下CPL 的功率为PCPL=48.5 kW，系统稳定。t31=0.3 s 时刻负荷功率减少至PCPL=26.8 kW。

图8 负荷功率下降时MCDCM的稳定性分析结果Fig.8 Analysis results of MCDCM stability when load power decreases

由图8（a）可知，当负荷功率减少时，系统广义Nyquist 轨迹在复平面中存在右移趋势，这表明系统存在更低的失稳风险，稳定裕度增加。

对时域仿真进行分析，在t31=0.3 s 时，系统负荷功率减少至26.8 kW，直流母线电压经暂升后恢复至额定电压水平，如图8（b）所示。通过电压波动程度可知，在负荷功率减少后系统稳定裕度上升，与频域分析结果相一致。

4 结论

本文针对MCDCM 拓扑结构，提出一种基于阻抗网络模型的开环传递函数分析方法来研究系统小扰动稳定性问题，得到如下结论。

（1）针对MCDCM 拓扑，首次将其划分为GVS 子系统、GCS 子系统和无源子系统（线路阻抗网络）。基于此提出阻抗网络模型的概念，并推导出与其等效的负反馈模型，以便于分析复杂直流微电网系统稳定性问题。

（2）基于阻抗网络模型的概念，本文所提阻抗网络模型的开环传递函数可如同传统阻抗比一样表征系统的小扰动稳定性问题，该性质为系统的小扰动稳定性判定及设计方法提供了一种新思路。通过频域分析和时域仿真验证了所提方法可用于改善系统稳定性。

附录见本刊网络版（http：//www.epae.cn）。