中低压柔性直流配电系统稳定性分析模型与机理研究综述

李鹏飞，李霞林，王成山，郭 力，彭 克，张 野，王 智

（1. 天津大学 智能电网教育部重点实验室，天津300072；2. 山东理工大学 电气与电子工程学院，山东 淄博255000；3. 南方电网科学研究院有限责任公司 直流输电技术国家重点实验室，广东 广州510663）

0 引言

2021 年3 月15 日召开的中央财经委员会第九次会议，首次明确提出要构建以新能源为主体的新型电力系统；且随着我国“双碳”（碳达峰以及碳中和）目标的提出，大力发展光伏、风电为代表的新能源势在必行。中低压柔性直流配电系统可实现高渗透率光伏、风电等新能源高效接入，灵活接纳电动汽车、大型数据中心、LED照明及通信设备等直流型负荷，减少电能变换环节以提升供配电效率，实现有功功率灵活控制，提高供电质量和可靠性［1-5］。基于柔性直流技术的直流配电系统有望广泛应用于高比例新能源接入、大规模工业园区等直流负荷密集、供电可靠性要求高的场合，成为未来城市配电网的重要补充，为构建以新能源为主体的新型电力系统提供新的解决方案。

相比于交流系统，直流配电系统内缺乏类似同步发电机机组的强自然惯量支撑单元，且由于高比例电力电子设备的接入，系统呈现低惯量、弱阻尼特性，因此稳定性问题较为突出［6-8］。此外，直流母线电压是衡量直流系统有功功率平衡的唯一标准，直流配电系统内不存在类似交流系统的功角及频率稳定等问题，维持直流母线电压稳定对直流配电系统稳定可靠运行十分重要［9-10］。

直流配电系统内，随着具有多时间尺度控制特性的电力电子设备以及高渗透率可再生能源的接入，源-网-荷-储及其交互作用导致系统存在低频及中高频多时间尺度小扰动稳定问题［11-14］。此外，直流配电系统存在共母线、多母分段、环网及多直流电压等级等多种复杂拓扑形式，使得直流配电系统小扰动稳定性机理更加复杂。基于状态空间模型的时域分析法（简称为状态空间法）以及基于等效阻抗模型的频域分析法（简称为阻抗法），是目前常用的2 类直流配电系统小扰动稳定性的建模和分析方法。状态空间法是在系统稳态运行点处进行线性化处理，得到系统状态空间矩阵，进而采用特征值、参数灵敏度以及参与因子法分析系统稳定性，但需要预先获取系统的详细信息，因此适用性受限。阻抗法通常选取某一公共分界点，将系统分为等效源、荷2 个子系统，分别得到2 个子系统频域阻抗模型（输出阻抗以及输入阻抗），进而通过奈奎斯特判据及其改进稳定性判据评估系统稳定性。与状态空间法不同，即使系统是黑匣子，无法获取系统详细信息，阻抗法依然可通过实时阻抗测量，获取阻抗频率特性，进而分析系统小扰动稳定性。需要指出的是，基于高阶数学模型的状态空间法和阻抗法，仅能够通过观测系统参数对根轨迹或奈奎斯特曲线等的影响分析系统稳定性变化规律，难以有效揭示系统稳定性机理。因此，适用于机理分析的降阶模型也引起了部分学者的关注。

在传统电力系统中，通常依据扰动大小将系统稳定性分为大扰动稳定以及小扰动稳定［15-17］。一般而言，小扰动稳定分析基于在稳态运行点进行线性化处理的简化模型。系统发生小扰动后，虽然不能回到原始运行状态，而是达到新的稳态运行点，但基于线性模型的分析结果仍然有效，仍可以采用小扰动稳定分析方法。但小扰动稳定分析无法体现系统的全局非线性特征，所得分析结果仅在局部有效。当系统遭受大扰动后，基于线性模型的分析结果难以准确、有效反映系统在较大范围内的稳定性变化规律及特征，此时则需运用基于非线性模型的大扰动稳定分析方法研究系统稳定性。

由于可再生能源具有间歇性和波动性，直流配电系统运行状态变化频繁且变化范围大，因而对直流配电系统进行大扰动稳定或暂态稳定分析，从全局角度评估系统稳定性十分有必要。时域仿真法以及基于李雅普诺夫函数LF（Lyapunov Function）的直接法，是目前常用的分析直流配电系统暂态稳定问题的分析方法。时域仿真法的核心思想是直接求解描述直流配电系统的非线性高阶微分-代数方程组，然后根据系统状态量的敛散性来判断系统稳定性［18-20］。尽管该方法直观，分析结果可靠，但分析结果不能定量刻画系统的稳定程度，无法为失稳（临近稳定）系统预防性（增强）控制提供指导，且计算量较大，因此具有一定的局限性。直接法通过比较表征系统能量的LF 值与表征临界能量的LF 值，评估系统的大扰动稳定性［21-22］。直接法无需对扰动后的系统变量进行积分运算，计算速度快，能够量化分析系统稳定程度，为系统预防性（增强）控制设计提供理论指导。但直接法的难点在于如何构造合适的LF，尤其是对于复杂直流配电系统。

面对接入设备多样化、直流网络复杂化及控制策略灵活化的中低压柔性直流配电系统，如何对其小扰动稳定和大扰动稳定问题进行有效梳理，厘清当前研究系统稳定机理的建模方法、分析思路，进而为未来复杂直流配电网稳定性机理研究和增强系统稳定性的控制策略设计提供一些思路和建议，是本文工作的主要出发点。本文首先梳理了直流配电系统几种常见的典型拓扑类型及其基本的控制策略，然后对典型控制策略下直流配电系统的小扰动稳定以及大扰动稳定问题的建模方法和相应机理分析进行了全面综述，最后对直流配电系统稳定性研究的重点方向进行了展望。

1 直流配电系统典型拓扑类型及控制策略

本节首先梳理直流配电系统几种常见的拓扑类型，进而概述其基本控制策略。

1.1 典型拓扑类型

直流配电系统根据实际场景及需求，可采用共母线结构［23-24］、环状或多母分段等复杂直流网络互联结构［25-26］以及多直流电压等级经直流变压器柔性互联结构［27-28］等拓扑形式，分别如图1（a）—（c）所示。

图1（a）所示的共母线拓扑是最基本的直流配电网系统组网形式。根据控制功能的不同，可将接入直流配电系统的设备分为直流电压控制单元和以恒功率控制单元为主的广义负荷2 类。直流电压控制单元通过直流电压控制策略维持直流网络电压稳定及功率平衡，采用恒功率控制的电力电子变流器、光伏和风电等新能源发电单元以及具备恒功率运行特性的负荷均可看作恒功率控制单元。根据直流配电系统电压等级以及接入设备的电压要求，电力电子变流器可采用常规拓扑，即DC-AC 变流器、DC-DC变流器（Buck、Boost 变换器等）以及模块化多电平换流器MMC（Modular Multilevel Converter）等多种类型。当光伏和风电等新能源、储能装置以及负荷分布比较广泛，可依据实际场景和需求将多源和多荷经环状或多母分段等复杂直流网络柔性互联，如图1（b）所示。当多个直流微电网邻近，或者须满足不同电压等级需求时，多直流母线电压间可通过DC-DC直流变压器，构建如图1（c）所示的多直流电压等级直流配电系统，实现多子系统间的电压匹配和功率交换，提高整个系统的稳定性和控制灵活性。

1.2 典型控制策略

直流配电系统通常采用分层控制架构，主要包含设备级以及系统级控制2 层，其中设备级控制仅利用就地测量信息，实现新能源出力或负荷波动、系统运行模式变化等暂态工况下快速功率平衡及稳定控制。协调控制及能量优化运行均属于系统级控制层，一般须基于通信网络，实现多子系统、多设备间运行数据状态共享及交互，最终达到系统全局协调及优化运行。本文重点考虑了设备级控制影响下的直流配电系统稳定性问题。因此，在具体对其小扰动和暂态稳定问题研究进行综述之前，有必要先介绍系统内直流电压控制单元及恒功率控制单元的典型控制策略。

1.2.1 直流电压控制单元的典型控制策略

直流电压控制单元的典型控制策略如图2 所示，可分为电压电流双环控制［29-30］、下垂双环控制［31］以及下垂单环控制［32-33］等。值得指出的是，当直流电压控制单元采用DC-AC 变流器时，内环一般采用基于dq旋转坐标系的电流内环控制。

对于采用主从模式的直流配电系统，直流电压控制单元通常采用图2（a）所示的恒直流电压控制策略。图中，udcref和udc分别为直流电压控制单元出口直流电压参考值和实际值；isref和is分别为直流电压控制单元电流内环的参考值和实际值；Gu（s）和Gi（s）分别为直流电压PI 控制器和电流内环PI 控制器的传递函数。当直流配电系统包含多个直流电压控制单元时，为实现直流电压控制及功率分配，通常采用图2（b）所示的电压下垂双环控制策略。图中，idc和Kd分别为直流电压控制单元输出直流电流和下垂系数。此外，也有文献采用电流下垂双环控制以及下垂单环控制，分别如图2（c）和图2（d）所示。

1.2.2 恒功率控制单元的典型控制策略

恒功率控制单元的典型控制策略如图3所示，可以分为定功率电流双环控制［34］、负载电压电流双环控制［35］、定功率单环控制［36］以及负载电压单环控制［37］等。图中，Pref和P分别为恒功率负荷CPL（Constant Power Load）功率设定值和实际值；uLref和uL分别为CPL 的负荷电压设定值和实际值；Gp（s）为有功功率PI控制器的传递函数。除上述控制外，光伏、风电等新能源通常采用最大功率点跟踪控制。

图3 恒功率控制单元的典型控制策略Fig.3 Typical control strategies of constant power control units

2 小扰动稳定问题研究

本节首先论述了基于详细数学模型的直流配电系统稳定性问题的研究现状，主要包含基于状态空间模型以及等效阻抗模型的2 种分析方法，然后对基于降阶模型的直流配电系统小扰动稳定性研究现状进行综述。影响直流配电系统小扰动稳定性的主要因素如图4 所示，主要包括：①源（直流电压控制单元）的变流器类型、控制模式、带宽以及多源间交互等；②负荷的类型、控制策略以及多荷间交互等；③源-网-荷间交互作用等。因此，在论述直流系统小扰动稳定机理时，将按照源、荷的详细动态以及源-网-荷之间交互的影响依次展开。

2.1 基于详细数学模型的小扰动稳定分析

2.1.1 基于状态空间模型的分析

（1）基本原理及分析方法。

图4 直流配电系统小扰动稳定性的主要影响因素Fig.4 Key influence factors of small-disturbance stability of DC distribution system

采用模块化建模思路，分别对直流电压控制单元、以恒功率控制单元为主的广义负荷以及直流网络的动态在平衡点处线性化，进行小信号建模，便可获得用于分析任意直流配电系统小扰动稳定性的状态空间模型的一般性表达，具体如图5所示。

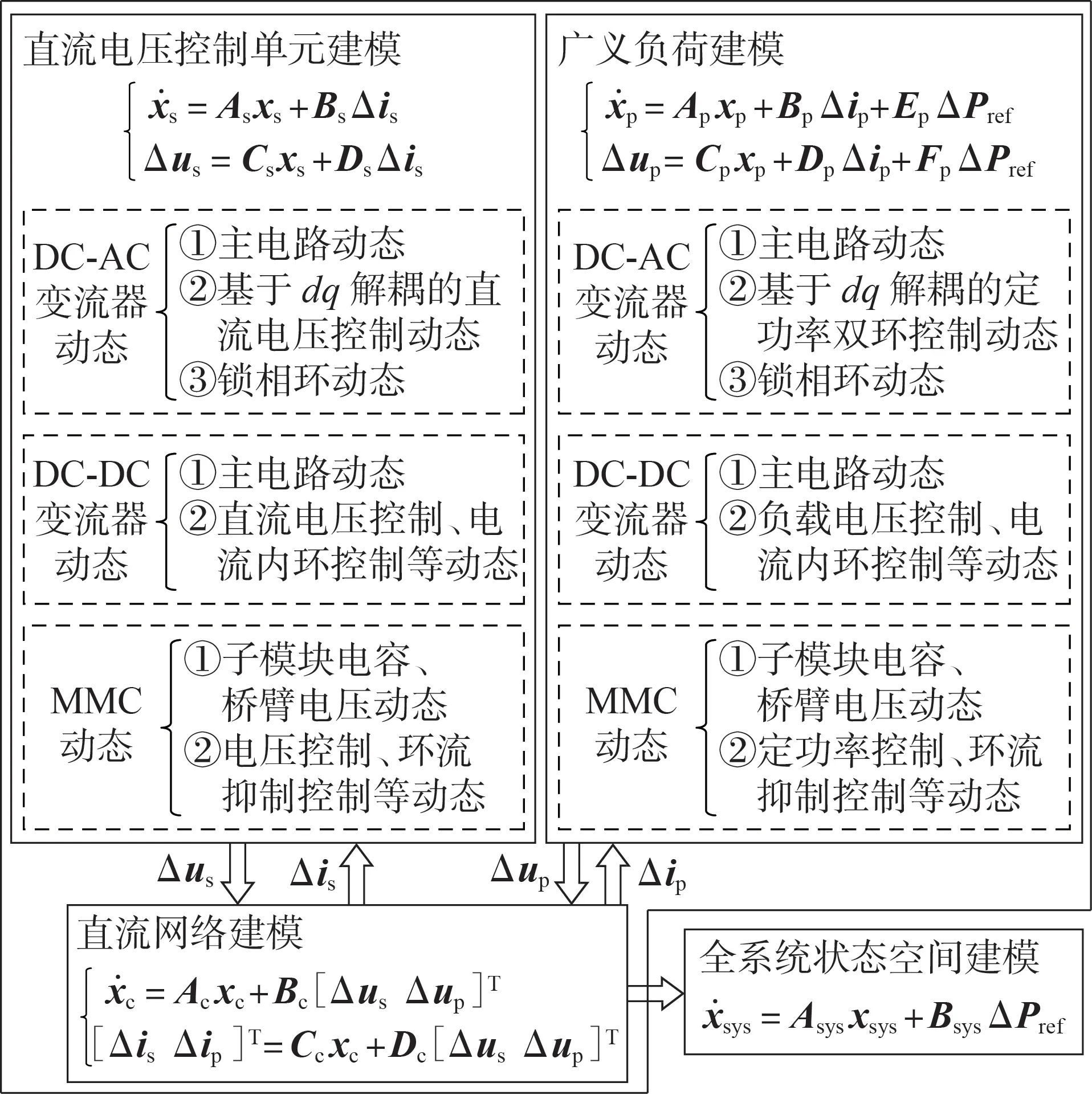
图5 状态空间法建模思路Fig.5 Modeling procedure of state-space method

直流电压控制单元状态空间模型如下：

其中，xs为直流电压控制单元的状态变量矩阵；Δus和Δis分别为直流电压控制单元出口处直流电压变化量矩阵和直流电流变化量矩阵；As和Bs分别为状态矩阵和输入矩阵；Cs和Ds分别为输出矩阵和前馈矩阵。

当直流电压控制单元所采用的变流器类型不同时，其状态矩阵As计及的详细动态也有所不同。采用DC-DC 变流器时，一般考虑直流电压控制、电流内环控制等控制动态［38-39］。对于DC-AC 变流器，则需要考虑基于dq解耦的直流电压控制动态等［30，34］。当采用MMC 时，还需考虑子模块电容、桥臂电压动态及环流抑制控制等的影响［40-41］。

分别对广义负荷和直流网络进行建模，通过接口变量耦合，最终形成全系统状态空间模型如下：

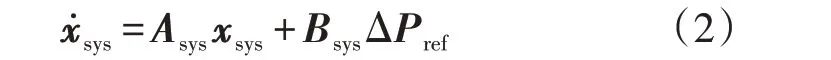
其中，xsys为全系统的状态变量矩阵；Asys和Bsys分别为全系统状态矩阵和输入矩阵；ΔPref为广义负荷功率参考变化量矩阵。

系统状态矩阵Asys包含了所有直流电压控制单元、广义负荷及直流网络的详细动态，进而可通过特征值、参与因子或灵敏度分析［38，42］等分析系统小扰动稳定性。

（2）研究现状。

a. 源（直流电压控制单元）的影响。

针对直流电压控制单元详细动态对系统稳定性的影响，很多学者针对基于不同类型变流器的直流系统展开了研究。文献［34］研究了基于两电平DCAC 变流器的直流系统低频稳定问题，发现直流电压控制环节及直流电容对系统主导低频模态影响较大，通过特征根分析发现随着直流电压控制比例系数减小，低频（2.96 Hz 左右）模态主导特征根向右半平面移动，系统稳定裕度减小。文献［31］比较分析了电压下垂以及电流下垂2 种模式对基于电压源型换流器（VSC）的直流微电网稳定性的影响，通过特征值分析及时域仿真发现下垂系数取值相同时，2种模式下系统直流电压低频（小于10 Hz）动态特性明显不同。文献［38，43］则在研究基于DC-DC 变流器直流系统高频稳定问题时，发现尽管在一定范围内增大下垂系数可提升多源均流效果，但同时会使系统高频模态特征根向右半平面移动，降低系统高频振荡模态的阻尼，可能导致系统高频谐振失稳。此外，增大直流电压控制比例系数会降低系统高频振荡模态的阻尼。可见，直流电压控制单元下垂、直流电压控制等环节的控制动态将影响直流系统的高、低频多时间尺度稳定性，且在不同频段的影响机理也有所不同。然而由于详细状态空间模型的高阶特性，尽管可以通过控制参数影响特征根的变化规律、参与因子法等探究直流电压控制单元控制动态对系统稳定性的影响，但仍然难以直观揭示造成不同频段稳定问题的影响机理。

b. 荷（广义负荷）的影响。

大量研究表明，高比例具有负电阻特性的CPL接入是恶化直流系统小扰动稳定性的重要原因。文献［44］研究了CPL 控制带宽对系统稳定性的影响，指出当CPL 控制带宽足够高时，可近似等效为负电阻；而当控制带宽较小，或者与所研究的稳定问题的时间尺度相接近时，应计及CPL 详细控制动态的影响。文献［34］发现随着DC-AC 变流器定有功功率控制环比例系数增大，系统高频（797 Hz 左右）模态特征根将由左半平面进入右半平面，系统将可能发生高频振荡。文献［45-46］研究了负载电压双环控制策略下的电动汽车充电站接入对直流系统稳定性的影响，发现系统低频模态主要与电动汽车充电站控制动态相关，高频模态则与充电站LC滤波参数相关，且随着互联充电站数量增加，主导特征根将向右半平面移动，系统稳定性降低。此外，文献［39］研究了感应电动机等动态负荷对直流微电网系统稳定性的影响。

c. 源-网-荷交互影响。

在直流配电系统中，直流电压控制单元、广义负荷与LC 环节间交互作用将影响系统稳定性。文献［47］发现由线路阻抗和直流母线等效电容构成的弱阻尼LC 环节与直流母线电压控制单元交互作用会影响系统高频稳定性，且并联直流电压控制单元数量越多，系统主导高频特征根将趋向右半平面，系统越易发生高频振荡。文献［32］在研究基于Buck 变换器的直流微电网稳定性问题时，发现随着源侧等效电阻减小，系统特征根将由左半平面进入右半平面，系统将发生高频振荡。文献［45］在研究电动汽车充电站接入对直流系统稳定性的影响时，也发现了类似的结论。此外，文献［38，43］发现增大直流线路电阻可以增大直流微电网主导高频模态阻尼，提高系统稳定性。然而，针对线路阻抗对系统稳定性的影响，文献［48-49］却得出了与文献［38，43］相反的结论。可见，不同系统及运行场景下，直流网络特性（线路阻抗）与源荷间交互动态对系统稳定性的影响机理可能不同，尤其在直流网络特性更加复杂的情况下。基于状态空间的参与因子分析虽然能够辨识影响系统主导模态的相关因素，反映源-网-荷交互对主导模态的共同作用程度，但也仅能提供相关数值结果，无法清晰揭示源-网-荷交互的本质机理。

（3）小结。

综上可知，源-网-荷及其交互动态均会影响直流配电系统多时间尺度小扰动稳定性，且在不同频段内，直流电压控制单元、广义负荷的详细控制动态以及源-网-荷交互动态对系统稳定性的影响机理可能不同。基于详细状态空间模型的分析方法能够建立全系统完整模型，进而评估、分析直流配电系统高、低频多时间尺度稳定性，且不受直流网络拓扑约束的影响。但由于详细状态空间模型的高阶特性，仅能提供表征系统稳定性的数值信息，通过特征值、参与因子及灵敏度等的变化规律被动观测系统参数对系统稳定性的影响，难以有效揭示系统多时间尺度稳定本质机理。此外，状态空间建模须预先获取系统详细信息，当系统详细动态未知时，其适用性受限。

2.1.2 基于阻抗模型的分析

2.1.2.1 基本原理及分析方法

阻抗建模与状态空间建模不同，即使系统是黑匣子，无法预先获取系统详细信息，依然可通过实时阻抗测量，获取系统阻抗频率特性，进而通过奈奎斯特判据及其改进判据评估系统稳定性。阻抗建模基本思路如图6所示。

图6 阻抗法的建模思路Fig.6 Modeling procedure of impedance-based method

对于单源单荷直流系统，其等效源荷阻抗模型如图6（b）所示［50］，系统直流母线电压和电流动态可表示为：

其中，Δubus和Δibus分别为母线直流电压和电流变化量；Δvin和Zo分别为直流电压控制单元等效直流电压源电压扰动量和等效输出阻抗；Δipref和Zin分别为广义负荷等效负载参考电流扰动量和等效输入阻抗。

对于多源多荷共母线系统，一般首先将其等效为图6（a）所示的并联电路模型，图中每个直流电压控制单元等效为直流电压源Δvsi与阻抗Zsi串联电路，广义负荷等效为直流电流源Δilj与阻抗Zlj并联电路。然后进一步等效得到图6（b）所示的等效源荷阻抗模型［51-52］，图中直流电压控制单元等效输出阻抗Zo等于源侧总并联阻抗，广义负荷等效输入阻抗Zin等于负荷侧总并联阻抗。

值得指出的是，直流电压控制单元等效输出阻抗Zo可包含其控制模式［49］、详细控制动态［53］以及多源交互动态［54］的影响。广义负荷等效输入阻抗Zin可包含其控制策略和带宽［51］、负荷类型［55］以及多荷交互动态［56］的影响。依据所得源侧输出阻抗Zo及荷侧输入阻抗Zin，可采用基于阻抗匹配的稳定性判据进行分析。基于阻抗的稳定性判据可分为2 类，分别如图7（a）和图7（b）所示。

图7 基于阻抗的稳定性判据Fig.7 Impedance-based stability criterion

一类基于系统源荷阻抗比Tm（Tm=Zo/Zin），也称为小回路增益（minor loop gain），包含Middlebrook判据、GMPM（Gain Margin and Phase Margin）判据、Opposing Argument 判据以及ESAC（Energy Source Analysis Consortium）判据等［37，57］，此类稳定判据针对阻抗比设定了相应的禁止域，只要阻抗比不进入该域，则系统稳定。另一类则基于系统母线处等效总阻抗Zbus，采用基于无源理论的稳定判据［33，58］，当满足Zbus（s）没有右半平面极点和Re｛Zbus（s）｝≥0 这2个条件时，系统稳定。基于阻抗比的稳定性判据需要明确的源荷划分点，而基于母线等效总阻抗的无源判据无需如此。

然而，当直流网络比较复杂，例如采用环状、多母分段以及多直流电压等级等拓扑时，往往不存在某一明确的源荷划分点，因此无法直接采用图7 所示的稳定性判据分析系统稳定性，但仍可通过基于等效电路建模的分析方法进行研究。下面首先综述基于阻抗模型的共母线直流系统小扰动稳定性研究现状，然后介绍复杂网络系统稳定性分析的相关内容。

2.1.2.2 研究现状

（1）共母线系统。

a. 源（直流电压控制单元）的影响。

直流电压控制单元等效阻抗模型如图8 所示。当系统中仅含1 个直流电压控制单元或采用主从控制模式时，可直接建立图8（a）所示的等效直流电压源Δvin串联等效输出阻抗Zo的电路及模型，其中等效输出阻抗Zo包含了直流电压控制单元的详细动态［50，59］。对于多源接入采用下垂控制的直流配电系统，可首先将每一个直流电压控制单元等效为直流电压源Δvsi与阻抗Zsi的串联电路，得到图8（b）所示的多源并联等效模型，进而从公共母线处求解得到直流电压控制单元总输出阻抗Zo，即所有直流电压控制单元等效输出阻抗。相比单源接入系统，直流电压控制单元总输出阻抗Zo包含了多源交互的影响。

图8 直流电压控制单元阻抗模型Fig.8 Impedance models of DC voltage control unit

文献［53］针对用于多电飞机的直流微电网，发现直流电压控制单元下垂系数增大，将导致源输出阻抗增大、负荷输入阻抗减小，两者在低频段发生交叉，可能影响系统低频稳定性。此外，直流电压控制带宽过小或过大，均有可能使源荷阻抗频率特性交互，影响系统稳定性。文献［53-54］发现随着直流电压控制单元并联数量增加，其等效输出阻抗减小，源输出阻抗频率特性将远离负荷输入阻抗，系统稳定性增强。文献［49］从阻抗建模角度探究了主从控制和下垂控制2 种控制模式对交直流混联配电系统稳定性的影响，发现主从控制模式下源变换器输出阻抗较大，负载变换器输入阻抗较小，负阻抗稳定边界较小；当采用下垂控制时，源输出阻抗较小，负载变换器输入阻抗较大，负阻抗稳定边界范围较大。可见，采用基于阻抗的分析方法时，是将直流电压控制单元对系统稳定性的影响直接反映在源侧输出阻抗Zo上，可通过观测输出阻抗Zo幅值／相位特性及奈奎斯特曲线变化规律观测、评估系统稳定性，但无法清晰阐明导致系统失稳的本质机理。

b. 荷（广义负荷）的影响。

广义负荷等效阻抗模型如图9 所示。当系统内仅含1 个广义负荷时，可直接得到图9（a）所示的等效输入阻抗模型。当系统存在多荷并联接入时，可首先得到图9（b）所示的多荷并联等效模型，进而从公共母线处得到负荷总输入阻抗Zin，即所有广义负荷的等效输出阻抗。相比单荷接入系统，此时负荷总输入阻抗Zin不仅包含每个广义负荷的详细动态，也计及了多荷交互动态的影响。

图9 广义负荷阻抗模型Fig.9 Impedance models of generalized load

在研究小扰动稳定性时，通常将CPL 在稳态运行点处进行线性化处理，得到其负电阻电路模型［54，60］。文献［51，59］考虑了DC-AC 变流器的详细定功率控制动态，发现定功率控制下DC-AC 变流器在低频段具有负阻抗特性，有功功率控制带宽增大，传输功率增加，均可能导致奈奎斯特曲线包围点（-1，0），使得系统发生低频振荡并失稳。文献［52］研究了基于DC-DC变流器的直流微电网中CPL详细动态对系统中高频稳定性的影响，发现CPL 在不同频段对系统稳定性的影响不同，CPL 功率增大将减小系统中频段（500 Hz）阻尼，增强高频段（5 kHz）阻尼。文献［53，56］从阻抗角度揭示了CPL数量增加，会导致频域阻抗倍增效应增强、负荷输入阻抗减小，进而降低系统稳定裕度。此外，文献［55］比较分析了阻性负荷、CPL 以及感应电机负荷对直流微电网稳定性的影响。可见，在广义负荷中，具有负阻抗特性的CPL 是影响直流配电系统稳定性的重要因素，CPL 详细动态在不同频段下对系统小扰动稳定的机理可能不同。虽然通过基于阻抗的频率特性以及稳定性判据能够观测CPL 对系统稳定性的影响，但是对于CPL在不同频段影响机理不同的原因有待研究。

c. 源-网-荷交互影响。

与上文状态空间法类似，一些文献从阻抗角度探讨了源-网-荷交互动态对含LC 环节直流系统稳定性的影响。文献［61］针对基于DC-AC 变流器的直流配电系统，发现并网模式下源荷阻抗在LC谐振频段附近的交互作用可能导致系统失稳，且CPL 渗透率水平的提高将显著降低系统稳定裕度。文献［59］基于阻抗频率特性以及奈奎斯特稳定性判据，发现LC滤波器会增大系统低频段输出阻抗，造成直流母线电压在输出阻抗峰值频率附近出现振荡。LC 滤波器输出等效电容越大，输出阻抗低频段的谐振峰值和相位越小，系统越稳定。此外，文献［50，60，62］从阻抗角度研究了基于不同类型DC-DC 变流器的直流系统中具有负电阻特性的CPL 与LC 环节交互作用引起的稳定性问题。

（2）复杂网络系统。

不同于共母线结构的直流配电系统，环状或多母分段等复杂网络系统往往不存在某一明显的源荷划分点，因此无法直接沿用经典的基于阻抗的稳定性判据分析系统稳定性。为研究复杂网络系统小扰动稳定性，文献［63-64］采用模块化建模思路，首先对系统内源、荷等接入设备进行戴维南／诺顿等效，并结合直流网络，得到全系统等效电路如图10所示。

文献［65-66］在图10 所示的等效电路的基础上，得到全系统节点导纳／阻抗矩阵，进而利用节点导纳／阻抗矩阵分析系统稳定性。文献［66］针对采用主从模式的直流微电网，通过分析由节点导纳矩阵得到的特征函数的极点评估系统稳定性，所提方法本质上仍是通过数值信息（极点）分析系统稳定性，因此针对直流微电网稳定性机理以及关键参数对系统稳定性的影响描述得并不是很清晰。文献［65］基于VSC 序分量动态向量谐波分析模型，建立了全系统等效电路模型，得到如式（4）所示的系统节点阻抗矩阵。进而分别通过节点阻抗矩阵Z中的自阻抗Zii和互阻抗Zij（i≠j）分析端口自身谐振特性及端口间交互作用对系统高频谐振的影响。

图10 复杂网络直流配电系统等效电路Fig.10 Equivalent circuit of DC distribution system with complex network

此外，一些学者将等效电路建模的思路用于分析多直流电压等级系统。文献［67］针对含光储多直流电压等级微电网，建立了等效受控源电路模型，在公共母线处将系统划分为源、荷两部分，进而通过系统阻抗模型的主导根轨迹分析系统稳定性。文献［68］通过直流系统等效回路增益，进而运用奈奎斯特稳定判据评估多电压等级系统稳定性。文献［69］将无源稳定判据应用于多电压等级系统分析，但所建模型依然呈现高阶形式，难以直观揭示系统稳定性机理。

2.1.2.3 小结

综上可知，相比于状态空间法，阻抗法不依赖系统详细信息，且可通过阻抗频率特性及稳定性判据研究源、荷及源-网-荷交互动态对系统小扰动稳定性的影响。表1 对基于状态空间模型和阻抗模型的2种分析方法进行了比较。

2.2 基于降阶数学模型的小扰动稳定分析

2.2.1 一些基本降阶思路

为降低建模复杂度，减小计算量，揭示系统小扰动稳定机理，对直流配电系统进行降阶建模是一种行之有效的方法。文献［42］在研究基于DC-DC 变流器的多母线直流微电网稳定性时，忽略具有快动态的直流电压控制的影响，提出了仅考虑下垂控制动态的降阶状态空间模型。文献［70］通过参与因子分析，辨识影响直流电压稳定的主导模态的强相关变量，忽略弱相关变量的影响，以实现DC-AC 变流器模型降阶，最终得到采用主从控制的直流配电系统降阶状态空间模型。上述降阶状态空间模型虽然可以有效减小模型复杂度和计算量，但所提方法仍无法清晰揭示直流系统小扰动稳定机理。

表1 不同小扰动建模分析方法比较Table 1 Comparison of different small-disturbance modeling and analysis methods

文献［71］提出一种适用于采用下垂控制的直流微电网简化阻抗模型，从零极点角度研究多源交互对直流微电网低频稳定性的影响机理，研究表明每个直流电压控制单元等效输出阻抗中均含有低频振荡模态的零点，因此若有多个具备这类特性的等效输出阻抗并联，会导致系统综合阻抗中出现含低频振荡模态的极点。但所提降阶方法建立在等效负荷输入阻抗较小的前提下，取系统总阻抗近似等于源侧输出阻抗，当无法忽略等效负荷输入阻抗时，所提降阶方法将失效。

文献［72］针对基于DC-AC 变流器的直流配电系统，通过参数灵敏度分析，忽略电压电流双环控制中积分系数的影响，最终通过降阶得到系统高频段振荡模态的解析表达式。文献［73］则采用类似方法研究了基于MMC 的柔性直流配电系统低频稳定问题，将MMC 等效为简化两电平模型，并忽略线路阻抗、桥臂电感等参数的影响，通过降阶得到低频振荡模态的解析表达式，发现MMC 子模块电容大小与振荡频率呈负相关，而子模块个数与振荡频率呈正相关。

文献［52］依据输入阻抗、输出阻抗频率特性在交叉点附近呈现感性或者容性，将其分别等效为RC、RL 电路模型，进而得到系统二阶特征方程，评估系统主导高频模态的阻尼特性。文献［35，74］采用类似的方法，研究了基于DC-DC 变流器的直流配电系统的低频谐振机理。但上述方法没有建立系统参数与等效电路间的直接联系，对于这样近似处理的缘由，以及导致源荷阻抗分别在不同频段呈现不同特性的根本原因描述得并不清晰，且未明确阐述关键控制参数对系统高、低频振荡特性的影响机理。

为清晰揭示直流系统不同时间尺度小扰动稳定机理，笔者所在团队相继提出了相应的降阶建模方法，从等效电路角度揭示了由直流电压控制主导的低频动态稳定机理及由电磁振荡回路主导的高频振荡稳定机理［75-77］。

2.2.2 基于等效电路模型的降阶思路

（1）由直流电压控制主导的低频动态稳定机理。

文献［75-76］针对采用下垂双环控制的多端直流MTDC（Multi-Terminal DC）系统，提出一种用于分析系统低频动态稳定机理的降阶电路模型。在直流电压控制单元建模过程中，忽略具有快动态电流内环的影响，得到经典PI 控制策略下的直流电压控制单元等效输出阻抗Zo如下：

其中，kpu和kiu分别为直流电压控制环节的比例系数和积分系数；Cs为直流电压控制单元出口电容。

由电路理论可知，等效输出阻抗Zo本质上由电阻、电感及电容并联组成，即：

其中，Rs和Ls分别为直流电压控制单元的等效电阻和等效电感。

由式（5）和式（6）易知，采用文献［75-76］所提降阶模型，直观地揭示了直流电压PI 控制参数的物理意义，即直流电压控制的比例系数将唯一决定等效输出阻抗Zo的电阻，且与其成反比；积分系数将唯一决定Zo中的电感，且与其成反比。进一步通过引入直流电压控制单元等效阻抗比K（s）并在低频段进行简化，将CPL 等效为RC 并联电路模型，最终得到全系统等效RLC降阶电路模型，如图11所示。由图11可知，由直流电压控制积分系数等效的电感与直流母线等效电容构成的LC 振荡回路是产生低频稳定问题的根本原因，由直流电压控制比例系数等效的电阻及CPL的负电阻特性均会影响系统低频模态阻尼。但所提方法仅适用于共母线系统，对于复杂系统的研究有待进一步加深。

（2）由电磁振荡回路主导的高频振荡稳定机理。

文献［77］建立了适用于直流微电网高频振荡机理分析的降阶电路模型，首先将采用下垂双环控制的直流电压控制单元出口电压动态表示为：

其中，ΔUset和Δus、Δis分别为等效直流电压源电压变化量和直流电压控制单元出口电压、电流变化量。

图11 多端直流系统等效RLC电路模型Fig.11 Equivalent RLC circuit model of MTDC system

考虑线路阻抗时直流电压控制单元如图12（a）所示。在主导高频模态处对直流电压控制单元进行降阶处理，将详细等效输出阻抗Zo等效为输出阻抗Zs，eq，具体如下：

其中，Rs，eq和Ls，eq分别为输出阻抗Zs，eq的等效电阻和等效电感。

将直流电压控制单元的下垂控制、直流电压控制及电流内环等控制环节对系统高频稳定性的影响，以可量化的等效电阻Rs，eq、等效电感Ls，eq形式呈现，其物理意义更加明确，并最终得到等效RL 串联电路模型。此时，直流电压控制单元可由图12（a）所示的详细阻抗模型等效为图12（b）所示的降阶形式。

图12 直流电压控制单元降阶建模过程Fig.12 Reduced-order modeling process of DC voltage control unit

进一步结合采用RC并联电路的CPL模型，得到全系统降阶电路模型，如图13 所示。由图13 可知，系统内LC 固有电气回路是产生系统高频振荡稳定问题的主导因素，直流电压控制单元控制动态可通过等效电阻Rs，eq、等效电感Ls，eq影响系统高频稳定性。但所提方法仅适用于共母线系统，且没有考虑CPL详细动态的影响。

图13 直流系统降阶模型Fig.13 Reduced-order model of DC system

综上可知，文献［75-77］虽然从等效电路角度揭示了由直流电压控制主导的低频动态稳定机理及由电气回路主导的高频振荡稳定机理，但均针对的是共母线系统，如何将所提针对设备的模块化降阶建模思路与复杂直流网络特性相结合，进而揭示复杂网络直流配电系统多时间尺度小扰动稳定机理，仍值得研究。

3 大扰动稳定问题研究

小扰动稳定可以确保系统在平衡点附近渐近稳定，但是当遭受大扰动时，系统的运行状态可能偏离平衡点较远，此时小扰动稳定分析使用的线性化模型与实际系统模型相差较大，因此通过小扰动稳定分析得到的结果可能是无效的，故而需要对直流配电系统进行大扰动或暂态稳定性分析。本节将依次对时域仿真法、直接法以及其他方法展开论述，进而分析这些方法的优点和局限。

3.1 时域仿真法

时域仿真法通过直接求解描述直流配电系统的微分-代数方程组以获得系统状态量和代数量随时间变化的轨迹，进而通过判断轨迹的敛散性来分析系统的稳定性［78］。时域仿真法能够适应复杂的非线性直流配电系统中各种元件模型和控制装置模型，且分析结果可靠，因而常作为其他大扰动稳定性分析方法的检验标准［77-79］。但是，时域仿真法也存在如下缺点：时域仿真较为耗时，且一次只能提供一个初始状态下的稳定结果；当系统被判定为不稳定（临界稳定）时，时域仿真无法为预防性控制器（增强性控制器）设计提供指导；时域仿真也不能提供有关系统稳定裕度的信息［80］。

3.2 直接法

直接法（李雅普诺夫第二法）通过判断系统的初始状态是否位于稳定平衡点SEP（Stable Equilibrium Point）的吸引域DA（Domain of Attraction）内来判断系统最终是否稳定［81］。因此利用直接法分析直流配电系统大扰动稳定问题的关键是刻画系统的吸引域。然而，对于大多数非线性自治系统ẋ=f(x)，刻画其真实吸引域RDA（Real Domain of Attrac⁃tion）往往非常困难，因而常见的且最为简单的方法是用RDA 的子集V (c)={x∈RN|V(x)≤c}近似RDA，此过程被称为估计吸引域［82］，其中V(x)为LF 或广义LF，N为系统状态变量的个数，c为大于0 的常数。LF 对吸引域的影响如图14 所示。从图14 中可以看出，LF 选得越合适，所估计吸引域的保守性就越低，即所选的LF 决定了所估计吸引域的保守性。因此构造合适的LF 是利用直接法分析直流配电系统大扰动稳定问题的关键。

图14 LF对吸引域的影响Fig.14 Influence of LF on DA

在传统交流电力系统暂态稳定分析研究中，通常忽略其损耗影响，此时广义LF 是自然存在的，其包含动能和势能2 个分量［22］，但是对于直流配电系统，LF 通常无法直接确定。然而，目前已有文献提出了一些构造LF 或广义LF 的方法，下文将逐一进行简要介绍，并梳理这些方法的优势和局限，以期促进直接法在直流配电系统暂态稳定性分析中的研究。

3.2.1 混合势函数法

R. K. Brayton 和J. K. Moser 于1644 年提出了混合势函数MPF（Mixed Potential Function）理论［83］。MPF与电路结构有关，可根据非线性电路中的电感、电容以及非储能元件进行构建，统一表示为［84］：

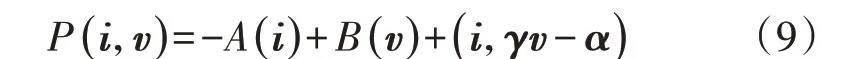
其中，-A(i)为电路中非储能元件的电流势函数；B(v)为电路中非储能元件的电压势函数；(i，γv-α)为电容和其他非储能元件的电压电流乘积。

虽然式（9）中的每一项都有清晰的物理意义，但是当电路中同时存在电感与电容时，判断式（9）对时间偏导的正负是困难的［83］。为了解决这一问题，R. K. Brayton 和J. K. Moser 在R和LC中至 少存 在1 类线性元件的假设下，给出了3 种构造广义LF 的方法和3条相应的稳定性定理，其中第1条稳定性定理和第2条稳定性定理要求R线性，第3条稳定性定理则要求LC线性。因而使用MPF 法对系统进行大扰动稳定分析时，应根据系统的特点选择合适的广义LF和相应的稳定性定理。此外，为扩大MPF理论的应用范围，文献［85］删去了R和LC中至少存在1类线性元件的假设。文献［86］利用负电阻电路揭示了R. K. Brayton 和J. K. Moser 提出的稳定性定理的不完整性，并在此基础上进行了完善。

MPF理论提出时间早，应用简便，且涉及电路参数，因而在直流配电系统大扰动稳定性分析中得到了大量应用。文献［87-90］考虑单源单荷的共母线直流配电系统结构，并忽略源、荷变流器的动态，将系统降阶为图15 所示的系统。然后利用该方法得到了降阶系统的大扰动稳定判据。文献［91-95］在此基础上利用La Salle 定理［96］刻画了降阶系统的吸引域，并探究了系统参数对吸引域的影响。上述文献都忽略了源变流器的控制动态，因而无法分析源变流器控制参数对系统稳定性的影响。基于此，文献［97-102］考虑源变流器的控制动态，利用MPF 法得到了系统的稳定判据。为了降低保守性，文献［98］同时考虑了源、荷变流器的控制动态。然而值得一提的是，文献［97-101］虽然考虑了源变流器的控制动态，但都只得到了使得广义LF 对时间偏导小于0 的条件，而文献［82］表明仅由该条件确定的区域可能比实际吸引域更大，因而考虑变流器控制动态时如何估计系统的吸引域仍需进一步研究。综上，MPF法虽简单易用，但难以同时考虑系统的物理动态和控制动态，因而具有一定局限性。

图15 直流配电系统等效降阶电路Fig.15 Equivalent reduced-order circuit of DC distribution system

3.2.2 TS模糊建模法

Takagi 和Sugeno 于1985 年提出了由“if-then”规则描述的TS 模糊模型［103］，其主要特点是可以用一组由非线性函数推导得到的相互连接的线性函数来拟合原函数，且当相互连接的线性函数足够多时，系统的模糊模型与原非线性模型等效［104］。Marx 首次提出用TS 模糊模型近似直流配电网系统模型［105］，并在文献［21］中提出构造LF 及估计吸引域的方法，详述如下。

步骤1：将非线性系统写为ẋ=A(x)x的形式，其中A(x)为一个包含状态变量的非线性矩阵函数。

步骤2：在平衡点周围选择一个小区域Ω，将其边界记为∂Ω。然后在该区域内求出A(x)每一个非线性项的最值，并分别用最值代替A(x)中的非线性项，因而每个非线性项对应2个线性矩阵Ai。

步骤4：增大Ω，同时更新Ωc，直至不存在使得步骤3 中线性矩阵不等式成立的矩阵M，此时Ωc即为系统的吸引域。

利用TS 模糊模型法可同时考虑系统的物理动态和控制动态，且容易扩展到高阶系统。文献［105］利用该方法分析了降阶直流配电系统，并刻画了吸引域。文献［106］将源、荷变换器的电压外环控制等效为一阶惯性环节，然后探究了电压外环带宽对系统吸引域的影响。文献［107］在此基础上利用该方法分析了2个CPL 对系统吸引域的影响。虽然TS模糊模型法在直流配电系统大扰动稳定分析中应用广泛，但矩阵Ai的数量与系统数学模型的非线性数量呈指数关系，这也大幅限制了该方法的应用场景。

3.2.3 平方和规划法

文献［108］最早提出用平方和SOS（Sum Of Squares）规划法估计多项式非线性系统ẋ=f(x)的吸引域，其主要思想是将难以验证的多项式函数正定性问题转换为可以有效验证的多项式函数是否可以表达为平方和形式的问题［109］。下面将介绍如何利用这一思想构造LF并估计吸引域。

为估计系统的吸引域ΩV，定义一个大小可变的区域Ωh={x∈RN|h(x)≤β}，其中h(x)为多项式函数，β为大于0 的常数。通过在约束条件Ωh⊂ΩV下最大化β从而达到最大化ΩV的目的［110-111］。对于不同的h(x)，ΩV会在不同维度下最接近RDA 边界，因而h(x)也被称为塑形函数。h(x)可以根据不同维度的重要性进行选择。图16 阐释了最大化ΩV的过程和塑形函数对吸引域的影响，图中ΔV(x)f(x)=V̇(x)，相应的优化问题如式（10）所示。

图16 不同塑形函数对吸引域的影响Fig.16 Influence of different shaping functions on DA

式（10）中的前3 个约束将ΩV限定于RDA 内。文献［112］对上述约束条件进行了等价变换，并利用代数几何中的Positivstellensatz 定理，将优化问题（式（10））转化为平方和规划问题（式（11））。

优化问题（式（11））中的约束s1(x)V(x)和βs2(x)会使得此问题变为非凸且难以求解的双线性半正定规划问题。一种常用的求解方法是Vs迭代法［113-114］，即交替固定V和s中的1 个，将优化问题变为线性半正定规划，然后利用MATLAB 中的SOSTOOLS 工具箱迭代求解［115］。限于篇幅，本文仅对平方和规划法进行简要介绍，具体参考文献［116-119］。

虽然平方和规划法将f限定为多项式。但文献［120］巧妙地利用V̇(x)与V̇(x)(x+x0)2正定性一致的性质，解决了由CPL 引入的非多项式非线性的问题，并利用该方法刻画出了降阶直流配电系统的吸引域。文献［121］在此基础上分析了源变流器控制动态对吸引域的影响。对于由CPL引入的非多项式非线性的处理，文献［122］提供了另一种求解思路——泰勒展开。相比于前几种方法，平方和规划法最大的优势在于它估计的吸引域相对而言保守性较低，但随着系统阶数、变量数目和多项式次数的增加，进行多项式分解所需要求解的半正定规划的规模快速增大，这也限制了该方法在高阶系统中的应用［109］。然而，文献［123］提出2种新的多项式分解方法——对角占优平方和、比例对角占优平方和。这2 种方法已被证明可大幅减少计算时间，因而该方法也有望被运用于更高阶系统。

3.2.4 二次对角化李雅普诺夫函数法

为了刻画高阶复杂系统的吸引域，B. P. Loop与C. J. Sullivan 提出了二次对角化李雅普诺夫函数BDQLF（Block Diagonalized Quadratic Lyapunov Function）法［124-125］。其主要思想是利用遗传算法搜索“好”的LF 来优化吸引域的形状［126］，然后利用遗传算法能够求解非凸优化问题的优势扩大吸引域。现将该方法详述如下。

步骤1：对非线性系统ẋ=f(x)线性化得到ẋ=Ax。

步骤2：用线性变换z=T-1(x-x0)将矩阵A化成约当型。

步骤3：形成待优化的LF如式（12）所示。

步骤2：求解优化问题（式（14））验证所得上界cmaxI的准确性，如果优化结果小于0，则说明步骤1得到的上界是准确的，否则减小cmaxI重新进行验证，直到优化结果小于0，将此时对应的cmaxI记作cmax。系统的吸引域为Ω={x∈RN|V(x)≤cmax}。

BDQLF 法对系统的阶数以及系统模型中包含非线性项的数目、类型并没有限制，因而其适用范围更广。文献［21］利用该方法估计了降阶直流配电系统的吸引域，文献［127］利用该方法估计了状态变量从6阶到75阶的电力电子化电力系统的吸引域。然而，该方法也有如下一些缺点：遗传算法编程实现复杂，且搜索速度慢；如何确定最佳种群规模和遗传代数尚不清楚；遗传算法容易收敛到局部最优解。

表2 对上述几种构造LF 或广义LF 方法的特点进行了总结。为使读者对上文介绍的4 种方法的保守性有更直观的理解，下面将分别利用这4种方法估计降阶直流配电系统的吸引域，见图17（系统平衡点被平移到坐标原点，RDA 边界是通过时域仿真得到的）。降阶直流配电系统的主要参数见文献［21］。

表2 不同LF构造方法比较Table 2 Comparison of different LF construction methods

图17 不同方法估计的吸引域Fig.17 Estimated DA by different methods

3.3 其他方法

3.3.1 逆轨迹法

逆轨迹法可刻画非线性系统ẋ=f(x)准确的吸引域［128］。其主要思想是在不稳定平衡点的稳定流形上取点作为初值对逆轨迹系统ẋ=-f(x)积分求得一系列轨迹，然后以逆轨迹的集合来估计穿过不稳定平衡点的稳定边界，该过程如图18 所示，其理论基础是江晓东教授提出的稳定域理论［129］。文献［21，130］利用该方法刻画了降阶直流配电系统的准确吸引域。然而，该方法基本上是图形化的方法，因而对于高阶系统（超过3 阶），利用该方法刻画吸引域将变得非常困难，此外无法用方程的形式描述利用该方法刻画的吸引域。

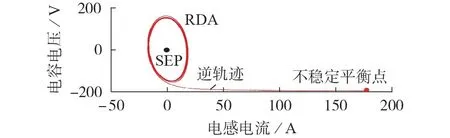
图18 利用逆轨迹法刻画RDAFig.18 Characterization of RDA by inverse trajectory method

3.3.2 非线性解耦法

当直流配电系统模型的阶数增加时，现有大扰动稳定性分析方法的复杂度和计算量会显著提高，因此其效率和有效性会大幅降低。基于此，文献［131］提出了基于耦合因子的非线性解耦方法。该方法的核心思想是首先将系统数学模型中的非线性泰勒展开并保留二次项，然后对保留二次项的系统进行线性变换，将原状态变量线性组合形成与系统特征根一一对应的新状态变量，选择互为共轭复数或耦合因子相近的2 个特征根对应的新状态变量作为耦合对，剩余的新状态变量作为孤立状态，最后通过非线性变换，将这些新的状态变量变换到新的空间，在新的空间里耦合对与耦合对之间、耦合对与和孤立状态之间没有耦合，从而将相互耦合的非线性系统转化为一系列解耦的一阶、二阶系统。对这些一阶、二阶系统进行大扰动分析会容易很多，分析结果的保守性也会显著降低，因此可以为系统参数设计提供更有意义的指导。

实际上，该方法分析结果的有效范围相较于小扰动稳定分析有所扩大。小扰动稳定分析利用系统平衡点处的线性模型来近似原系统，因此其分析结果只在平衡点附近的小范围内有效。而该方法保留了系统的二次项，因此其分析结果对高阶二次系统全局有效。对于系统模型泰勒展开中有高次项的系统而言，其分析结果的有效范围也有所扩大。为了更好说明这一点，图19 展示了直流配电系统中常见的由CPL 引入的非线性x/(x+1)（将平衡点平移到坐标原点）与线性化模型，保留了二次项模型之间的差别。图中，x为CPL 的端电压，y无具体物理含义，且x、y均为标幺值。显然只有当CPL 的端电压在-0.1～0.2 p.u.之间变化时，线性化模型与原非线性模型吻合度比较好，即只有在该区间内，小扰动稳定分析的结果才有效。对于保留二次项模型，即使电压在-0.4～0.45 p.u.之间变化，也可以很好地近似原非线性。然而，当系统遭受大扰动，使得CPL端电压的变化范围超出区间（-0.4，0.45）p.u.时，利用该方法得到的分析结果可能是无效的。

图19 不同模型对原函数的拟合比较Fig.19 Fitting comparison of different models to original function

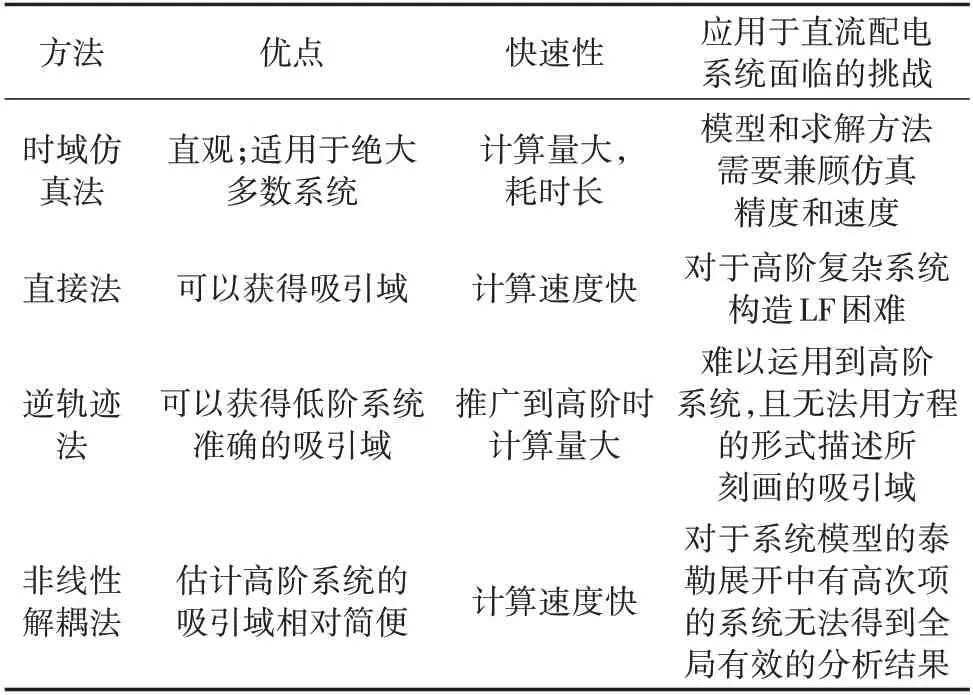
表3 不同大扰动稳定性分析方法优缺点比较Table 3 Comparison of advantages and disadvantages among different large-disturbance stability analysis methods

4 结论与展望

高渗透率光伏、风电等新能源和储能等直流型电源的发展，以及电动汽车、大型数据中心、LED 照明等直流型负荷的快速增长，使得基于柔性直流技术的直流配电系统必将成为以新能源为主体的新型电力系统的重要组成部分。系统内源-网-荷及其之间交互作用以及系统运行状态变化使得直流配电系统多时间尺度小扰动稳定性以及大扰动稳定问题十分复杂。

针对直流配电系统小扰动稳定性，基于详细数学模型（状态空间及阻抗模型）的分析方法可全面分析系统电气参数及控制参数对稳定性的影响，但难以有效揭示系统稳定性的本质机理。基于等效电路的分频段降阶模型可清晰地揭示不同时间尺度小扰动稳定机理，阐明影响系统稳定性的关键控制参数的物理意义。

针对直流配电系统大扰动稳定性，时域仿真法可直观分析系统受扰后的完整动态过程，但难以定量描述系统的稳定程度。直接法通过构造不同的LF 或广义LF 可估计共母线直流配电系统的吸引域，并探究电气参数及控制参数对系统吸引域的影响。

虽然目前国内外研究学者已经对直流配电系统的小扰动、大扰动稳定性开展了大量的研究，但仍存一些问题值得深入探讨，具体如下。

（1）直流配电系统稳定问题定义及分类。对直流配电系统稳定问题进行定义和分类是研究直流配电系统稳定性的基础。对于传统交流系统稳定性问题，国际上依据其物理机理已进行明确的定义和分类。此外，随着电力系统“高比例可再生能源和高比例电力电子设备（双高）”趋势的发展，IEEE和CIGRE组成的联合工作组于2020 年发布了“含高渗透率电力电子接口设备电力系统的动态行为特征与稳定性定义”的技术报告，在传统电力系统稳定性分类的基础上扩展出谐振稳定性和变流器驱动稳定性。谐振稳定性分为电气谐振和扭振。变流器驱动稳定性是指变流器的多时间尺度控制特性引起的宽频振荡，分为慢交互作用（slow interaction）和快交互作用（fast interaction）2 类。然而针对直流配电系统，由于对其稳定性的物理机理仍然缺乏深入的认识和理解，至今尚未形成统一的定义及分类方法。

（2）弱互联特性对直流配电系统稳定性的影响。在互联交流电网的直流配电系统中，随着互联功率、距离不断增加，或者因交流系统故障、检修等原因，使得直流配电系统与交流电网之间连接强度变弱，此时弱连接特性将可能对直流配电系统稳定性产生至关重要的影响。然而，目前鲜有研究涉及这一问题，因而如何有效揭示弱连接条件下直流配电系统的失稳机理以及如何提高系统稳定性，值得研究。

（3）直流配电系统多时滞多时间尺度交互稳定问题建模分析。系统级协调控制级优化运行与设备级控制间多时间尺度交互作用也会影响系统小扰动稳定性。此外，采用分布式协同控制策略时还会引入多时滞稳定问题。如何通过有效的建模方法，从机理层面厘清多时滞多层级控制对直流配电系统小扰动稳定性的影响，辨识影响系统不同时间尺度稳定性的关键环节及参数，进而指导控制器设计及参数优化，值得深入探讨。

（4）直流配电系统在线稳定性辨识及评估。由于缺乏类似同步发电机组的惯量支撑单元，直流配电系统自身具有低惯量、弱阻尼特性。虚拟同步发电机技术、虚拟惯量控制等控制技术以及直流电力弹簧、储能装置等暂态支撑单元均可有效提升系统惯量，改善系统小扰动稳定性。如何有效揭示考虑虚拟同步机控制及暂态支撑单元的直流配电系统多时间尺度小扰动稳定机理，在线辨识、评估直流配电网系统惯量和小扰动稳定性水平，进而指导系统虚拟同步机及暂态支撑单元配置、控制器参数优化，值得研究。

（5）直流配电系统小扰动稳定分析有效边界辨识及稳定分析方法选择。直流配电系统小扰动稳定分析结果是局部有效的，因此当扰动较大时，需进行大扰动分析。然而现有研究对小扰动分析有效性的稳定边界并不清晰。如何辨识小扰动分析的有效边界，进而根据所研究的具体问题合理选择大、小扰动分析方法，值得研究。

（6）复杂直流配电系统大扰动稳定性分析系统化分析工具。目前对于直流配电系统的大扰动分析大多集中于简单的共母线系统，但是面对网络更加复杂的直流配电网系统，仍然缺乏有效的分析工具。非线性解耦似乎是一个可行的方案，但是如何在保留高次项的情况下对系统解耦仍待进一步研究。此外，随着大数据技术的进步，基于数据驱动的人工智能方法在传统交流系统大扰动分析方面呈现出独特优势，但如何将该方法用于复杂特性直流配电系统，值得研究。

（7）稳定与控制的交互影响，及评估各种改进控制策略的统一分析框架。目前大部分稳定性分析均是对应于特定的控制策略。诚然，稳定离不开控制，但任何一种控制也必然面临稳定性的问题。当前也有很多学者提出能增强直流配电系统稳定性的控制策略，但鲜有学者考虑如何在一个统一的分析框架下去评估这些繁多的控制策略，是否这些控制策略在提升某种稳定性上存在某种必然的内在联系，或遵循某种基本规律。对上述问题的思考，不仅能帮助指导设计更好的控制器，或者从另一个角度出发，也能避免浪费更多研究资源和精力。