直流微电网高频振荡稳定问题的降阶建模及分析

李鹏飞，郭 力，王洪达，2，李霞林，王成山，冯怿彬，朱 想

（1. 天津大学 智能电网教育部重点实验室，天津300072；2. 海军勤务学院 供应管理系，天津300450；3. 国网浙江省电力有限公司电力科学研究院，浙江 杭州310014；4. 中国电力科学研究院（南京），江苏 南京210003）

0 引言

随着光伏、风电、燃料电池以及超级电容等分布式电源的发展，以及电动汽车、LED照明等直流负荷的增加，直流微电网由于控制结构简单，能够减少中间能量转换环节，提高能源利用效率和供电质量，得到了广泛关注［1-2］。然而由于高比例电力电子设备的接入，以及缺乏类似同步发电机组的惯量支撑单元，直流微电网面临着低频以及高频等宽频带振荡失稳问题［3-5］。文献［6］研究了采用下垂控制的直流微电网高频振荡稳定性，但由于采用的是具有高阶形式的详细建模分析方法，难以清晰地解释由于控制参数变化导致系统高频振荡的原因。如何有效揭示直流微电网高频振荡稳定机理，正是本文研究的出发点。

状态空间是常用的直流微电网稳定性建模分析方法。文献［7］以多并联恒功率负荷接入直流微电网为研究对象，建立了详细状态空间模型，发现随着恒功率负荷数量增加，系统主导高频特征值将向右移，稳定裕度降低，当主导高频特征值进入右半平面时，系统将发生高频振荡失稳。文献［8］基于状态空间模型，分析了LC滤波电感及电容参数对直流微电网高频稳定性的影响。文献［6，9］以采用下垂控制的直流微电网为研究对象，利用基于状态空间的特征根及灵敏度分析，发现下垂系数、直流电压控制比例系数增大，系统高频模态阻尼减弱，将导致直流微电网发生高频振荡。此外，基于阻抗模型的分析方法也同样适用于研究直流微电网高频振荡问题。文献［10］采用基于阻抗模型的Nyquist 判据分析了交直流混联配电系统采用不同系统级控制（主从控制及下垂控制）对系统稳定性的影响，发现采用下垂控制时，负阻抗稳定边界范围相较于主从控制时更大。文献［11］提出了基于并联阻抗的改进稳定性判据，克服了阻抗比判据由于微源和负载功率方向不同而无法有效判断的困难。然而上述研究均基于高阶形式的详细状态空间或阻抗模型，在控制参数变化时通过被动观测主导特征值或Nyquist 曲线变化趋势分析系统高频稳定性变化规律，均难以有效揭示变流器控制参数影响系统高频稳定性的本质机理。

为便于研究系统稳定性机理，对系统进行降阶建模是一种行之有效的方法。文献［12-13］从等效电路角度，建立了直流系统降阶电路模型，发现由直流电压控制积分系数等效的电感与母线电容构成的LC 振荡回路是产生低频振荡稳定问题的本质原因，然而所提建模方法难以用于分析直流微电网高频振荡稳定问题。文献［14］通过对影响模型阶数的关键参数进行灵敏度分析，进而忽略电压／电流双环控制中积分系数的影响，实现直流配电系统模型降阶，但所提降阶方法仅推导了时域下系统参数与高频振荡频率间的解析表达式，难以从等效电路层面清晰地揭示系统高频振荡机理。文献［15］通过观察电源、负荷等效输出／输入阻抗Bode 图在谐振频率处的相频频率特性，分别将其近似等效为RL串联电路或者RC串联电路模型，然而并没有建立系统参数与等效电路间的直接联系，没有得到等效电路的解析表达式，因此对于这样近似处理的缘由以及影响机理并不清晰。且没有考虑和分析下垂系数等控制参数对等效电路参数的影响，未明确阐述关键控制参数对系统高频振荡特性的影响机理。

为从等效电路角度揭示直流微电网高频振荡稳定机理，本文以一个典型的采用下垂控制的直流微电网为例，建立了全系统等效降阶电路模型，将直流电压控制单元控制动态对系统稳定性的影响，以可量化且具有明确物理意义的等效电阻、电感形式呈现。并基于完整降阶模型，提出了系统高频稳定性判据。在此基础上分析了直流电压控制单元控制参数对系统稳定性的影响。最后，在PSCAD／EMTDC软件中搭建了采用下垂控制的直流微电网详细电磁暂态仿真模型，对本文所提降阶模型及高频振荡稳定特性理论分析的有效性进行了验证。

1 直流微电网拓扑及其控制

本文研究的直流微电网拓扑如图1 所示。图中，ubus为公共直流母线电压；Cbus为公共母线处电容；vsi（i=1，2；后同）和isi分别为直流电压控制单元直流源电压和直流源输出电流；uoi和ioi分别为直流电压控制单元出口电压和输出电流；Rsi和Lsi分别为直流电压控制单元直流源侧电阻和电感；Csi为直流电压控制单元出口电容；Rei和Lei分别为直流电压控制单元出口线路的电阻和电感；Pcpl为恒功率控制单元输出功率；iop为公共母线流入恒功率负荷电流。系统包含2 个直流电压控制单元及1 个恒功率负荷。直流电压控制单元由模拟恒定直流电压源和双向Buck-Boost 型DC-DC 变流器构成，用于维持直流母线电压稳定及功率平衡。实际应用场景中用功率控制模式的互联装置或分布式电源，以及直流负荷等具备恒功率运行特性的设备均可看作恒功率负荷，在建模时可等效为一恒功率源与电容并联结构。

图1 直流微电网拓扑Fig.1 Topology of DC microgrid

直流电压控制单元控制策略如图2（a）所示，直流电压控制单元控制包含下垂控制、直流电压控制以及电流内环控制3 个环节，为便于描述，省略表示直流电压控制单元编号的下角标。图中，Io，set和uo，set分别为直流电压控制单元输出电流和直流电压设定值；Rd为下垂系数；is，ref为内环电流参考值；ds为输出占空比；Guu(s)和Guc(s)分别为直流电压控制器和电流内环控制器传递函数，具体表达式如式（1）所示。

其中，kpu和kiu分别为直流电压控制比例系数和积分系数；kpi和kii分别为电流内环控制比例系数和积分系数。

2 直流微电网高频降阶建模

本节首先推导了直流电压控制单元降阶模型，进而结合恒功率负荷模型，得到全系统降阶电路模型，并在此基础上提出了直流微电网高频稳定性判据。

2.1 直流电压控制单元降阶建模

在稳态运行点进行线性化处理，可得直流电压控制单元小信号传递函数模型如图2（b）所示。图中，μ为双向DC-DC 变流器电流转换系数，且满足μ=Vs/Uo，Vs和Uo分别为DC-DC 变流器低压侧直流电压源电压和出口电压稳态值；Δuo，set和Δuo分别为直流电压控制单元直流电压设定值和实际值的变化量；Δio为直流电压控制单元输出电流变化量；Gin（s）为电流内环闭环传递函数，如式（2）所示。

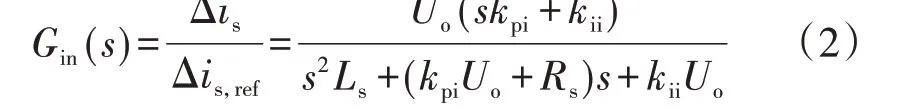
其中，Δis，ref和Δis分别为电流内环控制的电流参考值和直流源输出电流的变化量。

图2 直流电压控制单元控制策略及其传递函数模型Fig.2 Control strategy and transfer function model of DC voltage control unit

结合图2（b），直流电压控制单元出口直流电压动态可进一步表示为：

其中，ΔUset和Zu分别为等效直流电压源电压变化量和详细等效输出阻抗，具体表达式如式（4）所示。

其中，Gs（s）为直流电压控制动态对直流电压控制单元等效输出阻抗影响的传递函数。

结合图1 和式（3），可得直流电压控制单元详细阻抗模型如图3（a）所示。图中，Δubus为公共直流母线电压变化量。

为实现模型降阶，且保留Zu主导高频模态附近的频率特性，首先将s=jω0（主导高频模态虚部）代入Gs(s)，其中ω0为主导模态振荡频率，并按照式（5）所示的处理方式将其等效为一阶环节Gs，eq(s)。

结合式（5）和式（6），详细等效输出阻抗Zu可进一步降阶为等效输出阻抗Zu，eq，具体表达式如下：

Zu，eq=RdGs，eq(s)=Rd(ks+kqs)=Ru，eq+sLu，eq（8）

其中，Ru，eq和Lu，eq分别为Zu，eq的等效电阻和等效电感。

此时，直流电压控制单元可由图3（a）所示的详细阻抗模型等效为图3（b）所示的降阶形式。等效降阶输出阻抗Zu，eq本质上是直流电压控制单元详细控制动态在等效电路模型中的直接映射，因此可从等效电路角度，借助等效输出阻抗Zu，eq量化分析直流电压控制单元下垂控制、直流电压控制及电流内环控制等控制环节对系统高频稳定性的影响，从而揭示直流微电网高频稳定性机理。当计及直流电压控制单元线路阻抗时，可将等效降阶输出阻抗Zu，eq与线路阻抗合并，得到图3（c）所示的直流电压控制单元最终等效RL 串联电路模型。图中，Ze，eq为直流电压控制单元等效总阻抗；Re，eq和Le，eq分别为直流电压控制单元等效总电阻和等效总电感。

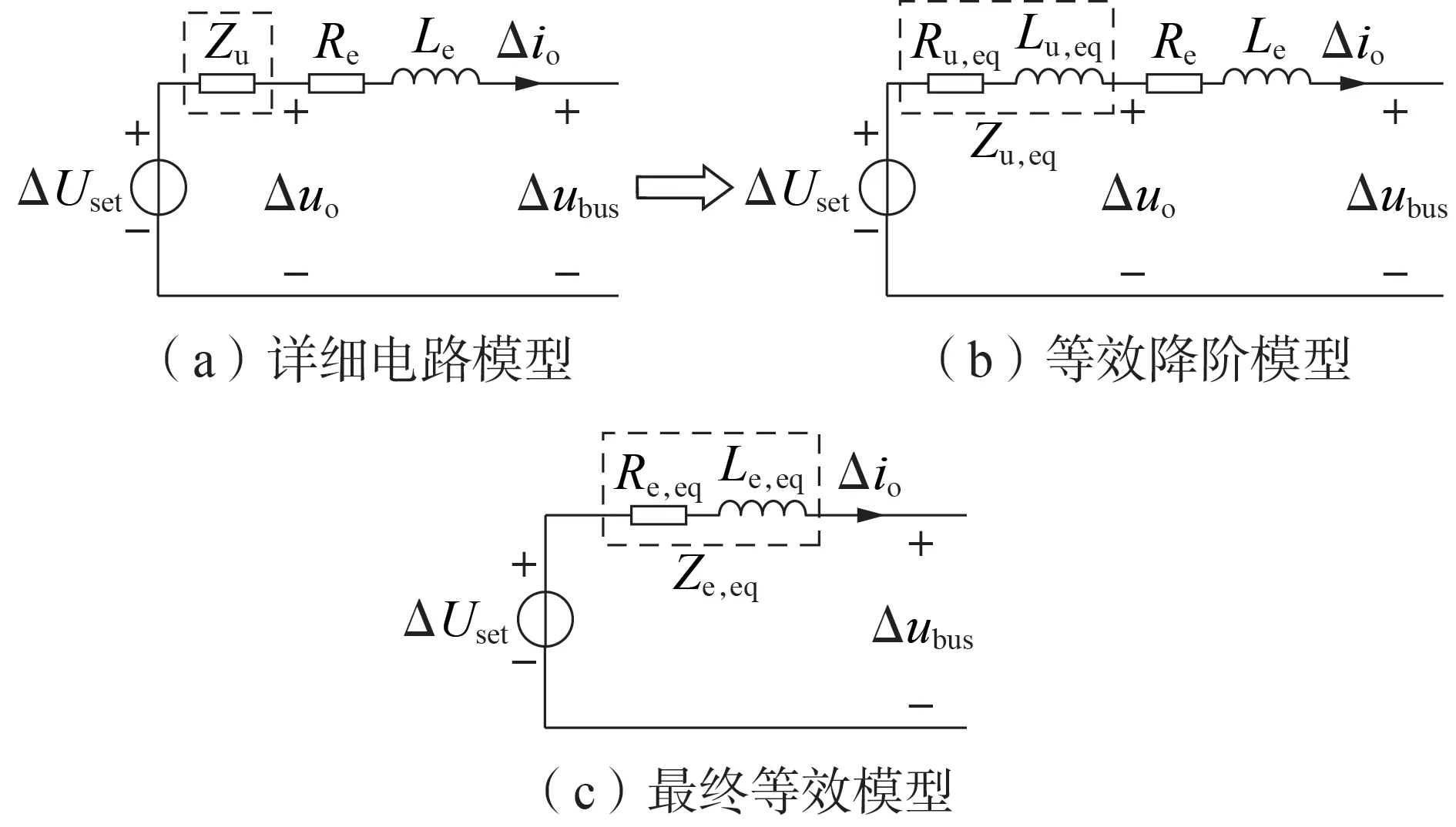
图3 直流电压控制单元降阶建模过程Fig.3 Reduced-order modeling process of DC voltage control unit

2.2 直流微电网模型

结合上文所得直流电压控制单元模型，可最终得到直流微电网全系统详细阻抗模型以及等效降阶电路模型，分别如图4（a）和4（b）所示。图中，Δidis为恒功率负荷的扰动电流；Rp，eq为恒功率负荷的等效电阻，具体表达式如式（9）所示。

图4 直流微电网模型Fig.4 Model of DC microgrid

其中，α和β为稳定性判据的2 个判据因子。当α和β均大于0 时，系统稳定；而当任一判据因子小于0时，将存在右半平面极点，系统将发生高频振荡。

综上可知，直流电压控制单元等效总电感及恒功率负荷母线电容构成的LC振荡回路，是直流微电网产生高频振荡的物理电路基础。直流电压控制单元各个控制环节将直接影响等效串联电阻和电感的大小，进而影响系统高频稳定性。基于所提降阶模型，可通过等效电阻、电感量化分析直流电压控制单元控制动态对系统高频稳定性的影响，从本质上揭示系统高频振荡稳定性机理。

3 基于降阶电路模型的直流微电网高频振荡特性分析

3.1 下垂控制直流微电网基本参数

不失一般性，本节以图1 所示的直流微电网为例，采用所提降阶模型分析系统高频稳定性。系统基本参数如附录中表A1所示。

3.2 直流微电网高频振荡特性分析

3.2.1 下垂系数的影响

设下垂系数Rd由0.2增大至1.2，采用详细阻抗模型和等效降阶模型时系统特征根变化情况见图5。由图可知，随着Rd增大，采用详细阻抗模型和等效降阶模型时系统主导高频特征值均向右移动，并进入右半平面，此时系统将发生高频振荡。可见采用等效降阶模型时主导高频特征值变化趋势与详细阻抗模型一致，验证了所提等效降阶模型的有效性。

图5 Rd 对系统特征根的影响Fig.5 Influence of Rd on system eigenvalues

采用等效降阶模型时，直流电压控制单元等效阻抗以及判据因子变化情况分别如图6和图7所示。由图可知，下垂系数Rd增大，直流电压控制单元等效电阻Ru，eq负电阻特性随之增强；当下垂系数Rd>0.8时，将导致直流电压控制单元等效总电阻Re，eq由正变负，判据因子α<0，系统将发生高频失稳。

图6 Rd对等效阻抗的影响Fig.6 Influence of Rd on equivalent impedances

图7 Rd 对判据因子α和β的影响Fig.7 Influence of Rd on α and β

可见，采用详细阻抗模型时，仅能通过下垂引起的特征值变化，被动观测下垂系数对系统稳定性的影响；而采用所提降阶电路模型时，可清晰揭示下垂系数增大，使得直流电压控制单元等效负电阻特性增强，进而诱发系统高频振荡这一本质机理。

3.2.2 直流电压控制比例系数的影响

设直流电压控制比例系数kpu由0.2 增大至1.6，采用详细阻抗模型和等效降阶模型时特征根变化情况如图8 所示。可见随着kpu增大，采用详细阻抗模型和等效降阶模型时系统主导高频特征值均向右移动，并进入右半平面，此时系统将发生高频振荡。

图8 kpu对系统特征根的影响Fig.8 Influence of kpu on system eigenvalues

采用等效降阶模型时，直流电压控制单元等效阻抗以及判据因子变化情况分别如图9 和图10 所示。由图可知，kpu增大，直流电压控制单元等效电阻Ru，eq负电阻特性随之增强；当kpu≥1时，将导致直流电压控制单元等效总电阻Re，eq由正变负，判据因子α<0，系统将发生高频振荡；当直流电压控制比例系数kpu在一定范围范围内变化时，等效电感变化很小。

图9 kpu对等效阻抗的影响Fig.9 Influence of kpu on equivalent impedances

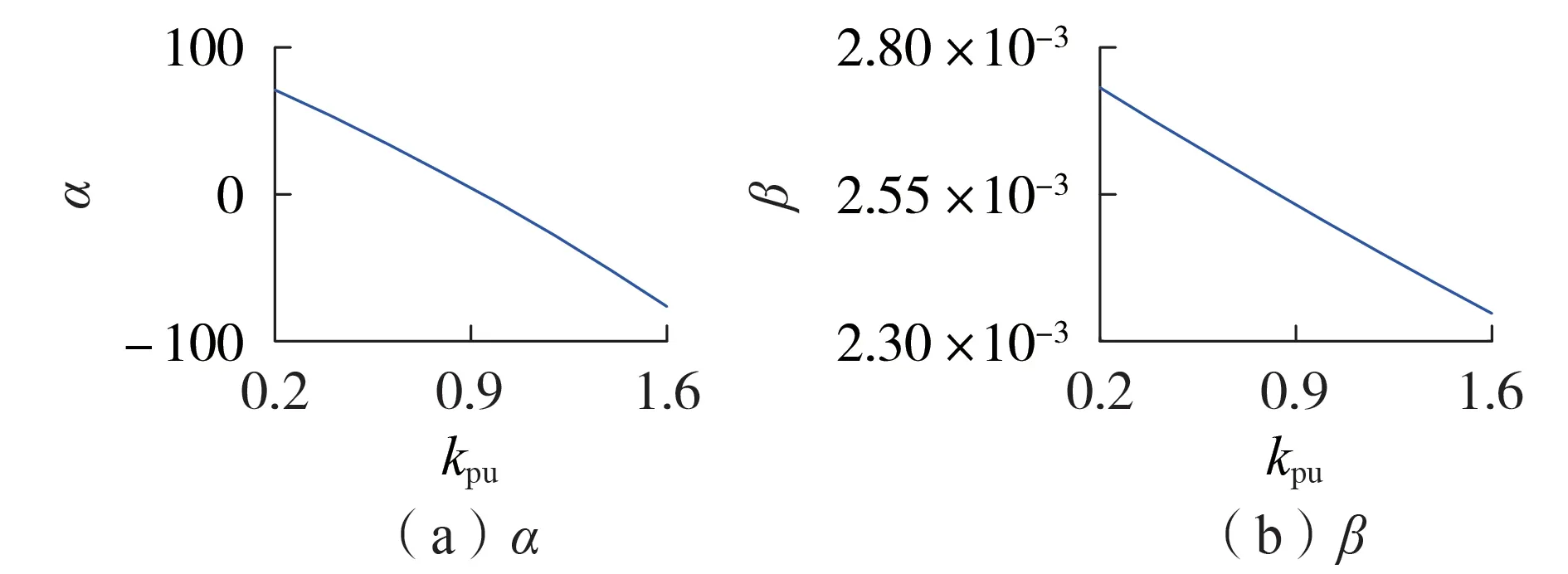
图10 kpu对判据因子α和β的影响Fig.10 Influence of kpu on α and β

3.2.3 电流内环控制比例系数的影响

设电流内环控制比例系数kpi从0.005 增大至0.035，采用详细阻抗模型和等效降阶模型时系统特征根变化情况如附录中图A1所示。由图可知，随着kpi增大，采用详细阻抗模型和等效降阶模型时系统主导高频特征值均向左移动，并进入左半平面。

采用等效降阶模型时，直流电压控制单元等效阻抗以及判据因子变化情况分别如附录中图A2 和图A3 所示。由图可知，当kpi较小时，直流电压控制单元等效电阻Ru，eq负电阻特性较强，直流电压控制单元等效总电阻Re，eq<0，判据因子α<0，系统将发生高频失稳；随着kpi增大，直流电压控制单元等效电阻Ru，eq负电阻特性减弱，直流电压控制单元等效总电阻Re，eq将由负变正，判据因子α和β将均大于0，系统稳定。

3.2.4 线路阻抗的影响

直流电压控制比例系数kpu取1，线路电阻Re从0.01 Ω 增大至0.08 Ω 时，采用详细阻抗模型和等效降阶模型时系统特征根变化情况如附录中图A4 所示。由图可知，随着线路电阻Re增大，采用详细阻抗模型和等效降阶模型时系统主导高频特征值均向左移动，并进入左半平面，系统稳定性增强。

采用等效降阶模型时，直流电压控制单元等效阻抗以及判据因子变化情况分别如附录中图A5 和图A6 所示。由图可知，当线路电阻Re较小时，直流电压控制单元等效总电阻Re，eq<0，判据因子α<0，系统将发生高频失稳；随着Re增大，由于直流电压控制单元等效电阻Ru，eq不变，直流电压控制单元等效总电阻Re，eq将由负变正，判据因子α和β将均大于0，系统稳定。

线路电感Le从0.15 mH 增大至0.35 mH 时，采用详细阻抗模型和等效降阶模型的系统特征根变化情况如附录中图A7 所示。由图可知，随着线路电感Le增大，采用详细阻抗模型和等效降阶模型时系统主导高频特征值均向虚轴靠近，但并未穿越虚轴。采用等效降阶模型时，直流电压控制单元等效阻抗以及判据因子变化情况分别如附录中图A8 和图A9 所示。由图可知，当线路电感Le从0.15 mH 增大至0.35 mH时，判据因子α和β始终大于0，系统稳定。

4 仿真验证

为验证本文所提高频等效降阶模型的有效性，在PSCAD／EMTDC 软件中搭建图1 所示的直流微电网详细电磁暂态仿真模型，系统基本参数如附录中表A1所示。

4.1 控制参数的影响

4.1.1 下垂系数的影响

为验证下垂系数对系统高频稳定性的影响，分别取下垂系数Rd等于0.5 和1，t=3 s 时，恒功率负荷功率突然增加，直流母线电压动态如图11所示。由图可知，当Rd=0.5时，负荷扰动后直流母线电压经短暂波动后迅速恢复稳定；而当Rd=1 时，受扰后直流母线电压发生高频振荡，振荡频率约为2 205 rad／s，与理论计算结果2 231 rad／s 十分接近，仿真结果与上文理论分析一致，验证了所提降阶模型的有效性。

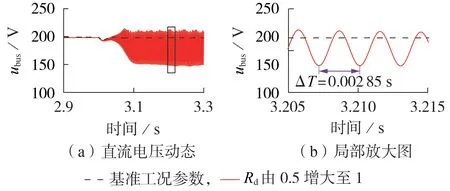
图11 Rd变化时的仿真结果Fig.11 Simulative results when Rd varies

4.1.2 直流电压控制比例系数的影响

为验证直流电压控制比例系数kpu对系统高频稳定性的影响，分别取kpu等于0.5和1，t=3 s时，恒功率负荷功率突然增加，直流母线电压动态如图12所示。由图可知，当kpu=0.5 时，负荷扰动后直流母线电压经过短暂波动后迅速恢复稳定；而当kpu=1时，直流母线电压发生高频振荡，振荡频率约为2 244 rad／s，与理论计算结果2 248 rad／s 几乎吻合。此外，当直流电压控制比例系数增大时，直流母线电压发生高频振荡，与上文理论分析一致。

图12 kpu变化时的仿真结果Fig.12 Simulative results when kpu varies

4.1.3 电流内环控制比例系数的影响

为验证电流内环控制比例系数kpi对系统高频稳定性的影响，分别取kpi等于0.02和0.004，t=3 s时，恒功率负荷功率突然增加，直流母线电压动态如附录中图A10 所示。由图可知，当kpi=0.02 时，负荷扰动后直流母线电压经过短暂波动后迅速恢复稳定；而当kpi=0.004时，直流母线电压发生高频振荡，振荡频率约为2 167 rad／s，仿真结果与上文理论分析一致，所提降阶模型的有效性得到了验证。

4.2 线路阻抗的影响

为验证线路阻抗对系统高频稳定性的影响，设置以下4种工况下进行仿真验证：工况1，Re=0.04 Ω，kpu=1；工况2，Re=0.08 Ω，kpu=1；工况3，Le=0.15 mH；工况4，Le=0.3 mH。其他参数如附录中表A1 所示。t=3 s 时，恒功率负荷功率突然增加，直流母线电压动态如附录中图A11 所示。由图可知，当线路电阻较小，即Re=0.04 Ω 时，直流母线电压受扰后发生高频振荡；当Re增大至0.08 Ω时，负荷扰动后直流母线电压经过短暂波动后迅速恢复稳定。可见增大线路电阻可有效减弱直流电压控制单元控制动态导致的负电阻特性的影响，但线路电阻过大会导致较大的稳态母线电压跌落。此外，当线路电感变化时，系统受扰后仍能恢复稳定。该仿真结果与上文理论分析一致。

4.3 有源阻尼控制环节的影响

为增强系统高频稳定性，文献［9］提出了基于低通滤波的有源阻尼方法，即在直流电压控制单元下垂控制的电流反馈回路串联图2 虚线框所示的有源阻尼控制环节Gdamp(s)，具体表达式如下：

采用与式（5）相同的降阶处理方法，可进一步得到Gs(s)的等效形式Gs，eq(s)，其等效比例项系数ks和微分项系数kq具体表达式如附录中式（A1）和式（A2）所示。基于上述推导，可进一步得到直流电压控制单元等效降阶阻抗的电阻及电感参数。采用有源阻尼控制，下垂系数Rd由0.2增大至1.2，直流电压控制单元等效阻抗以及判据因子变化情况分别如图13和附录中图A12所示。

图13 加入有源阻尼后Rd对等效阻抗的影响Fig.13 Influence of Rd on equivalent impedances with active damping

由图13 和图A12 可知，与常规控制相比，采用有源阻尼控制时直流电压控制单元等效电阻Ru，eq为正，负电阻特性明显减弱，且当下垂系数变化时，直流电压控制单元等效总电阻Re，eq始终为正，判据因子α和β始终大于0，系统稳定性显著提高。

为进一步验证有源阻尼控制的有效性，在PSCAD／EMTDC 软件中进行仿真测试，取Rd=1，直流母线电压动态如图14 所示。初始阶段，不投入有源阻尼环节，t=3 s 时，恒功率负荷功率突然增加，由图可知，直流母线电压发生高频振荡。t=3.4 s 时投入有源阻尼环节，由图可知，直流母线电压快速收敛并恢复稳定运行，验证了所提降阶建模方法的有效性。可见，采用所提降阶建模方法，可清晰揭示加入有源阻尼可以弱化直流电压控制单元等效负电阻特性，进而提高系统高频稳定性。

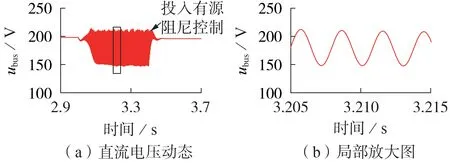
图14 加入有源阻尼后的仿真结果Fig.14 Simulative results with active damping

4.4 不同控制参数的影响

当多直流电压控制单元控制参数不同时，依然可采用所提降阶建模方法有效降低系统复杂度，从等效电路角度分析系统高频稳定性。以直流电压控制比例系数不同为例进行说明。由图9（a）可知，直流电压控制单元直流电压控制比例系数增大，将导致直流电压控制单元等效电阻Ru，eq负电阻特性增强，系统稳定性减弱。当多直流电压控制单元控制参数不同时，虽然无法得到全系统二阶降阶模型，进而得到稳定性判据，但依然可通过降阶电路模型的主导特征根分析控制参数对系统稳定性的影响。当2 号直流电压控制单元直流电压控制比例系数取1，1 号直流电压控制比例系数kpu1由0.2 增大至1.6，其他参数如附录中表A1 所示时，采用详细阻抗模型和等效降阶模型的系统主导特征根变化情况如图15（a）所示。由图可知，随着kpu1增大，采用详细阻抗模型和等效降阶模型时系统主导高频特征值均向右移动，并进入右半平面，此时系统将发生高频振荡。

然后对直流电压控制单元控制参数不同时进行仿真验证，即2 号直流电压控制单元直流电压控制比例系数恒定取1，1 号直流电压控制比例系数kpu1分别取0.5 和1，t=3 s 时，恒功率负荷功率突然增加，扰动后直流母线电压动态如图15（b）所示。由图可知，当kpu1=0.5 时，负荷扰动后直流母线电压能恢复稳定，而当kpu1增大至1 时，直流母线电压发生高频振荡，与上文理论分析一致。因此，当多直流电压控制单元控制参数不同时，仍然可采用本文所提降阶建模方法，从等效电路角度研究控制参数以及物理参数对系统高频稳定性的影响。

图15 kpu1对系统稳定性的影响Fig.15 Influence of kpu1 on system stability

5 结论

本文建立了适用于直流微电网高频振荡机理分析的降阶模型，从等效电路角度研究了直流微电网高频振荡稳定问题，主要贡献和结论如下：

（1）将直流电压控制单元降阶为等效RL串联电路，将恒功率负荷等效为与母线电容并联的负电阻模型，进而考虑直流电压控制单元接入母线的线路阻抗，得到全系统等效电路模型；

（2）通过在主导高频模态处进行降阶处理，将直流电压控制单元下垂控制、直流电压控制及电流内环等控制环节对系统高频稳定性的影响，以可量化的等效电阻、等效电感形式呈现，物理意义更明确；

（3）下垂系数、直流电压控制比例系数增大和电流内环控制比例系数减小均会导致直流电压控制单元等效负电阻特性增强，易使得系统发生高频振荡；

（4）基于低通滤波的有源阻尼方法，可有效减弱直流电压控制单元负电阻特性，提高系统稳定性。

如何将所提降阶建模方法用于分析控制策略更加灵活多样、网络拓扑更加复杂的直流微电网，是值得下一步深入思考和研究的问题。

附录见本刊网络版（http：//www.epae.cn）。