中压直流配电系统等效降阶建模及控制参数设计

朱 琳，赵学深，王一振，郭 力，刘海涛，袁宇波，卢 浩

（1. 天津大学 智能电网教育部重点实验室，天津300072；2. 天津市智慧能源与信息技术重点实验室，天津300072；3. 中国电力科学研究院有限公司，北京100192；4. 国网江苏省电力有限公司电力科学研究院，江苏 南京210096）

0 引言

相较于传统中压交流配电系统而言，中压直流MVDC（Medium Voltage DC）配电系统在能源效率、配电容量、配电损耗、建设成本等方面具有明显的优势，所以MVDC 配电系统是未来配电系统的发展趋势［1-2］。恒功率负荷的负电阻特性、控制参数不合理等因素都可能会导致MVDC配电系统出现稳定性问题［1-4］，为此采用准确的稳定性分析模型以及控制参数设计方法是十分有必要的。虽然全阶模型能够详细描述直流系统的动态特性，但建模过程复杂，模型阶数也比较高，难以直接指导控制参数设计［3-4］。因此，为降低直流系统动态特性分析的复杂性，降阶建模是非常有必要的［5-8］；同时，为尽量避免因控制参数不合理而导致直流系统出现稳定性问题［9］，以整个直流系统动态特性为设计目标的控制参数设计方法得到了国内外学术界和工业界的广泛关注［10-12］。

准确的直流系统等效降阶模型是开展系统动态特性分析的基础。利用常规降阶建模方法得到直流系统降阶模型的过程可大致分为2 步。第1 步为建立各个换流器在其单独运行时的闭环降阶模型。文献［5］中，在换流器单独运行时的电压控制带宽远高于下垂控制的前提下，电压控制参数就可以被忽略，进而换流器就可以等效降阶为输出电压由下垂控制器所决定的受控理想直流电压源。然而，当上述前提不成立时，所建立的换流器降阶模型将无法准确反映实际情况。第2 步为利用系统拓扑将各个换流器闭环降阶模型连接起来以建立整个直流系统的闭环降阶模型。文献［8］基于换流器的RLC 降阶模型，结合系统拓扑建立了直流系统降阶模型（二阶模型），并从解析的角度分析了电压PI 控制参数等因素对系统动态特性的影响。文献［9］辨识了电压源换流器（Voltage Source Converter）的主导特征根中参与度较高的状态变量，然后基于瞬时功率理论建立了换流器新型降阶模型，最后结合配电系统拓扑建立了11 阶的直流配电系统降阶模型。综上所述，利用常规降阶建模方法能够建立用于评估直流系统动态特性的闭环降阶模型，但很难为以整个直流系统动态特性为设计目标的控制参数设计提供必要的开环降阶模型支撑。

控制参数是决定直流系统动态特性的关键因素。换流器在单独运行时的控制参数设计方法已经非常成熟，所以换流器在单独运行时一般不会出现稳定性的问题。但当多个换流器构成一个直流系统时，各换流器间就会存在动态交互，另外恒功率负荷的负电阻特性会减小系统阻尼，多方面因素的叠加可能最终导致系统出现稳定性问题。针对上述因素所造成的直流系统稳定性问题，文献［11］基于所提出的模块化多电平换流器降阶模型，提出了一种能够有效提高直流系统稳定性的附加阻尼控制方法；在此基础上，文献［12］提出了提高换流器运行性能的附加功率阻尼控制方法。虽然文献［11-12］提出的方法能够有效解决直流系统出现的稳定性问题（该稳定性问题可以通过优化控制参数主动规避［9］），但以整个直流系统动态特性为目标的控制参数设计方法鲜有介绍。基于所建立的直流系统降阶模型，文献［13］提出了一种直流系统电压控制器参数设计方法，实现了直流系统振荡频率及阻尼比的定性定量设计，但仅讨论了换流器参数完全相同时的场景，并没有讨论各个换流器间参数不一致的情况。

针对上述问题，本文以MVDC 配电系统为研究对象，基于所提出的开闭环逐步等效降阶建模方法，逐步建立计及换流器间动态交互的开环和闭环等效降阶模型，并利用状态反馈控制方法以及所提出的MVDC 配电系统控制参数设计方法实现系统振荡频率及阻尼比的定性定量设计。首先，建立了MVDC配电系统的等效降阶电路模型以及计及换流器间动态交互的开环等效降阶模型；其次，建立了计及换流器间动态交互的闭环等效降阶模型，并提出了一种MVDC 配电系统控制参数设计方法；然后，以某MVDC 配电系统为例进行了控制参数的定性定量设计；最后，基于RT-BOX 硬件在环实验平台，验证了理论分析的合理性。

1 计及换流器间动态交互的开环等效降阶模型

1.1 系统拓扑及其等效电路模型

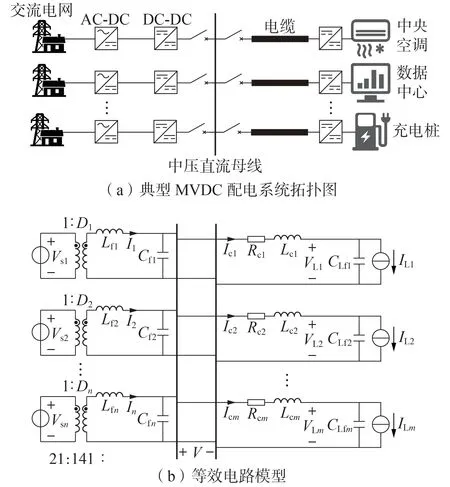
图1 典型MVDC配电系统拓扑及其等效电路模型Fig.1 Topology of typical MVDC distribution system and its equivalent circuit model

对如图1（a）所示的MVDC配电系统中的相关电力电子装置进行等值处理，得到如图1（b）所示的MVDC配电系统等效电路模型［14］。图1（b）中，Vsk（k=1，2，…，n，其中n为VSC 的台数）为第k台DC-DC VSC（即VSCk）的理想直流输入电压源；Dk和Ik分别为VSCk的占空比和输出滤波电感电流；Lfk和Cfk分别为VSCk的输出滤波电感和输出滤波电容；V为直流母线电压；Rch和Lch（h=1，2，…，m，其中m为恒功率负荷的个数）分别为第h条电缆线路的线路电阻和线路电感；Ich和ILh分别为第h条电缆线路上的电流和注入到第h个恒功率负荷的电流，其中ILh可为正值或负值，为正值时表示是真正的恒功率负荷，为负值时表示是风机和光伏等可再生能源［8，14］；CLfh和VLh分别为第h个恒功率负荷的输入滤波电容和输入电压［14］。由此，图1（b）所示的MVDC 配电系统等效电路模型可由n+2m+1阶微分方程描述。

1.2 等效降阶电路模型

当用等效简化模型［3］表示多个并联运行的恒功率负荷时，图1（b）可以被简化为图2（a）。基于开闭环逐步等效降阶建模方法的第1 步，并利用戴维南和诺顿等效定理，将图2（a）等效为图2（b）所示的等效降阶电路模型。图2 中，Cfeq为所有输出滤波电容Cfk并联后的等效输出滤波电容；CLfeq为所有输入滤波电容CLfk并联后的等效输入滤波电容；Rcable和Lcable分别为等效电缆线路的线路电阻和线路电感［3］；Vseq为理想直流输入电压源；Leq为等效输出滤波电感；IL为等效恒功率负荷的电流，即所有恒功率负荷电流ILh的累加；Peq为等效恒功率负荷功率；Deq为等效降阶模型的占空比；I为等效降阶模型的输出滤波电感电流。

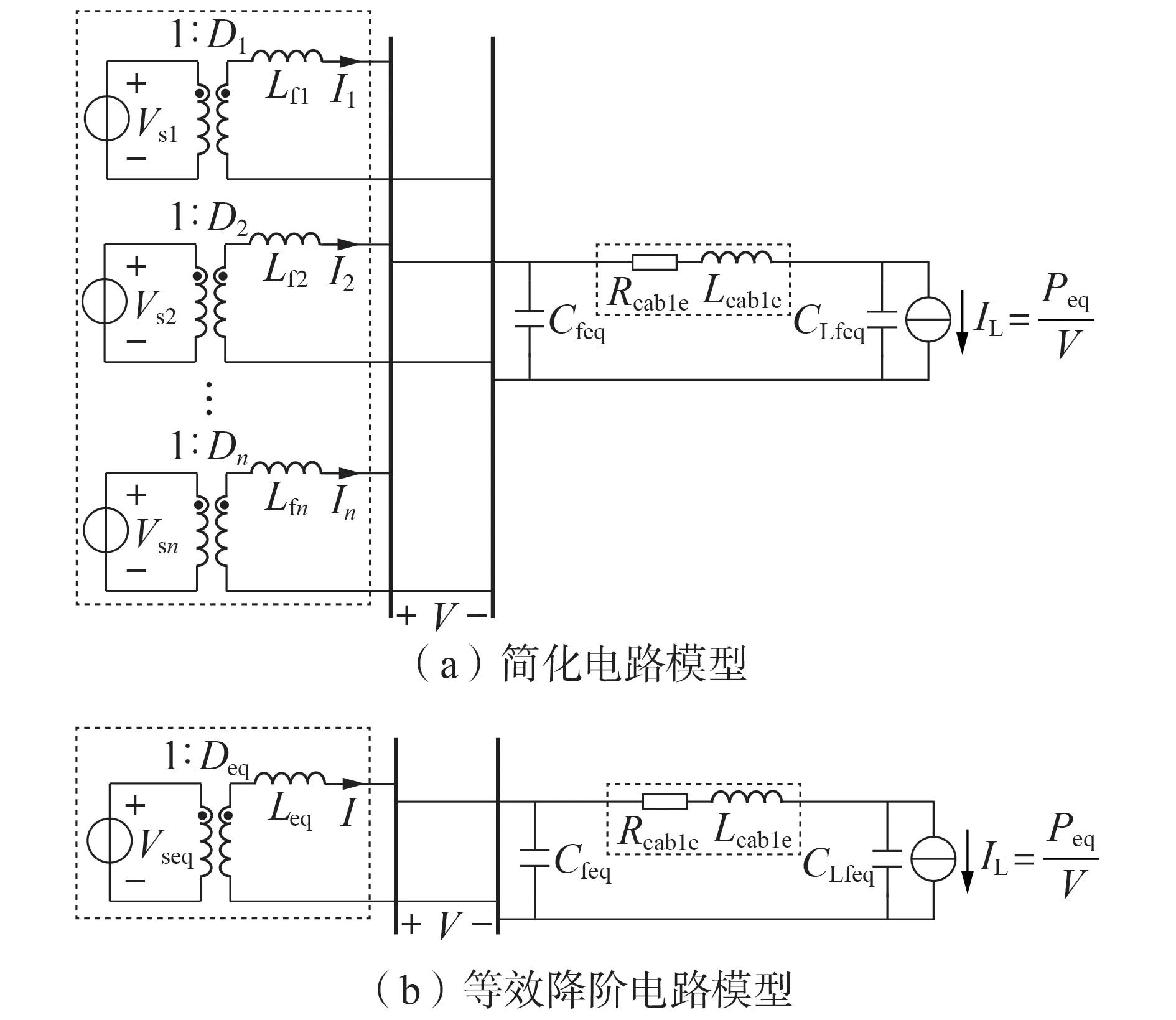
图2 简化电路模型及其等效降阶电路模型Fig.2 Simplified circuit model and its equivalent reduced-order circuit model

其中，ω0和ζ0分别为MVDC 配电系统的无阻尼自然频率和阻尼比；ωcz和ζcz分别为电缆线路引入零点所对应的固有振荡频率和阻尼比；ωcp和ζcp分别为电缆线路引入极点所对应的固有振荡频率和阻尼比；Ceq为等效输出滤波电容。

传递函数Gvdk_cable(s)的幅频曲线如图3 所示。图中，f0=ω0（/2π）；fcz=ωcz（/2π）；fcp=ωcp（/2π）。

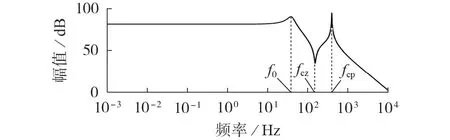
图3 传递函数Gvdk_cable（s）的幅频曲线Fig.3 Magnitude-frequency curve for transfer function Gvdk_cable（s）

由图3和式（3）可知，ωcz由Lcable和CLfeq共同决定，并不会受到MVDC 配电系统中控制参数的影响［15］。当ωcz与ω0间的比值小于5 倍频时，电缆线路就会对MVDC 配电系统的动态特性造成负面影响，严重时可导致系统出现稳定性问题。此时，可以利用状态反馈控制解决该问题［14］，具体内容将在第2 节进行详细介绍。由自动控制原理可知，当ωcz与ω0间的比值大于5 倍频时，电缆线路的影响就可以被忽略［16］。当忽略电缆线路时，图2 中的Cfeq和CLfeq就并联得到Ceq，此时MVDC 配电系统中的多个滤波环节最终可等效降阶为一个LC滤波环节。

对 于VSCk而 言，Dk(s)至V的开 环传递 函数Gvdk(s)的表达式就会变为：

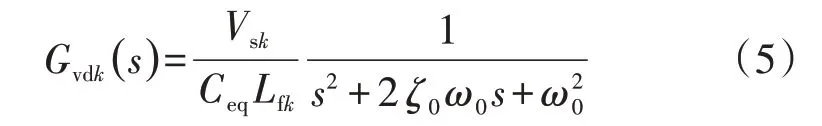
开环传递函数Gvdk(s)就是VSCk的计及换流器间动态交互的开环等效降阶模型，不仅计及了VSCk自身的滤波参数，还计及了其他换流器的滤波参数。由式（2）可知，ζ0<0，说明MVDC 配电系统的等效降阶电路模型存在2个不稳定的极点，后续将在第2节介绍如何设计控制参数保证MVDC 配电系统的稳定性。

2 计及换流器间动态交互的闭环等效降阶模型及控制参数设计

利用开闭环逐步等效降阶建模方法的第2 步和第3 步，建立计及换流器间动态交互的闭环等效降阶模型，如图4所示。

由图4 可知，利用开闭环逐步等效降阶建模方法可得到MVDC配电系统（多个VSC并联）最终的等效降阶模型（单个VSC）。考虑到MVDC 配电系统中各VSC 通过下垂控制来实现功率分配，故等效降阶模型的控制结构中也配置了下垂控制。另外，MVDC 配电系统及其等效降阶模型的控制结构中均包含状态反馈控制环节，其原因将在2.1 节详细阐述。

2.1 计及状态反馈控制的等效降阶建模

本文采用状态反馈控制方法主要是基于以下2个方面的考虑［14］。一方面，因恒功率负荷的负电阻特性，传递函数Gvdeq(s)呈现负相的不稳定状态，并且电压PI 控制器并不能有效改变电压控制回路增益相角裕度。本文所采用的基于泰勒展开的状态反馈控制方法的优势在于能将传递函数Gvdeq(s)控制成含正相稳定状态的传递函数Gsvdeq(s)，满足了MVDC配电系统对稳定性的需求。另一方面，当ωcz与ω0间的比值小于5 倍频时，电缆线路会对MVDC 配电系统的动态特性造成负面影响，严重时可导致系统出现稳定性问题。此时，可利用基于泰勒展开的状态反馈控制方法将无阻尼自然频率ωf调整至合理值，以满足上述要求。利用所建立的计及换流器间动态交互的闭环等效降阶模型中的状态反馈控制传递函数频域曲线，就可以查看状态反馈控制的效果。特别说明，虽然ω0和ωf都是无阻尼自然频率，但ω0仅由滤波参数决定（见式（2）），而ωf则由滤波参数和状态反馈系数共同决定（见式（14））。

由图4（a）可知，MVDC 配电系统中各个VSC 均配置了状态反馈控制。计及状态反馈控制后的VSCk占空比Dk(s)变为：

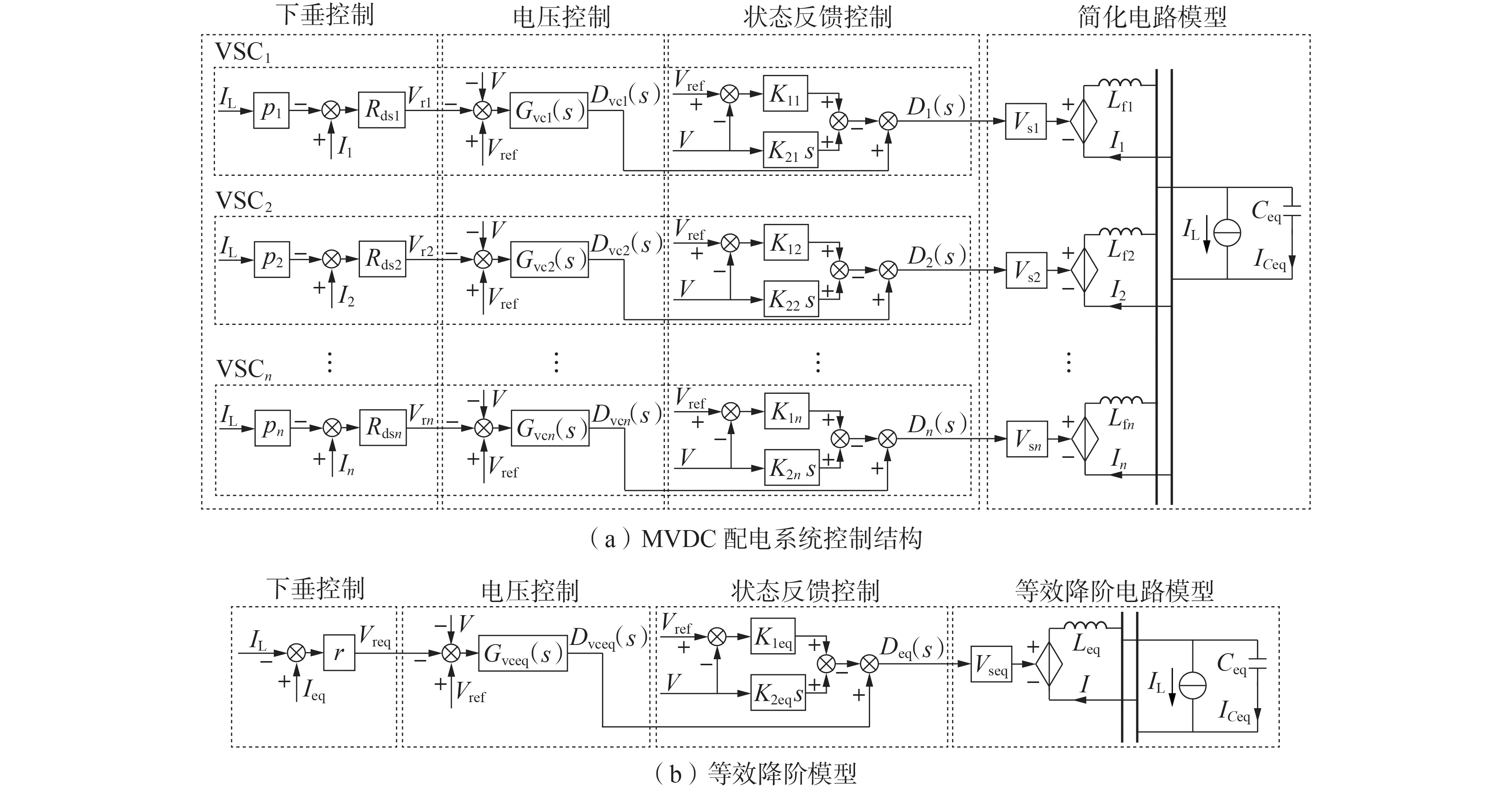
图4 MVDC配电系统控制结构及其等效降阶模型Fig.4 Control structure of MVDC distribution system and its equivalent reduced-order model

由式（9）可知，Gsvdk(s)就是VSCk的计及换流器间动态交互的闭环等效降阶模型中的状态反馈控制传递函数。Gsvdk(s)不仅计及了VSCk自身的状态反馈增益，还计及了其他换流器的状态反馈增益。

联立式（6）和式（11），Dvceq(s)至V的传递函数Gsvdeq(s)的表达式变为：

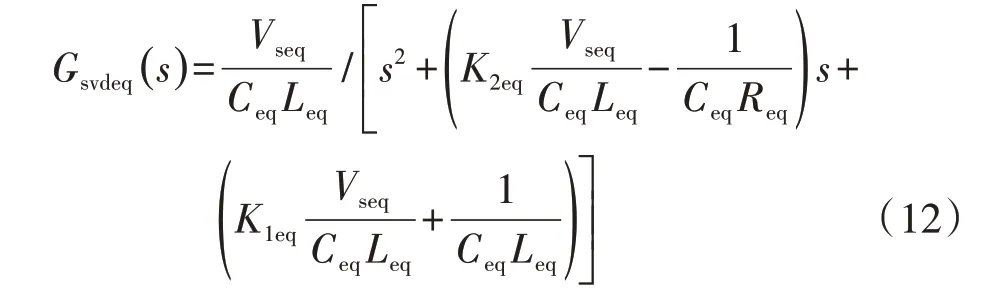
式（12）可以写成如式（13）所示的典型二阶系统形式。

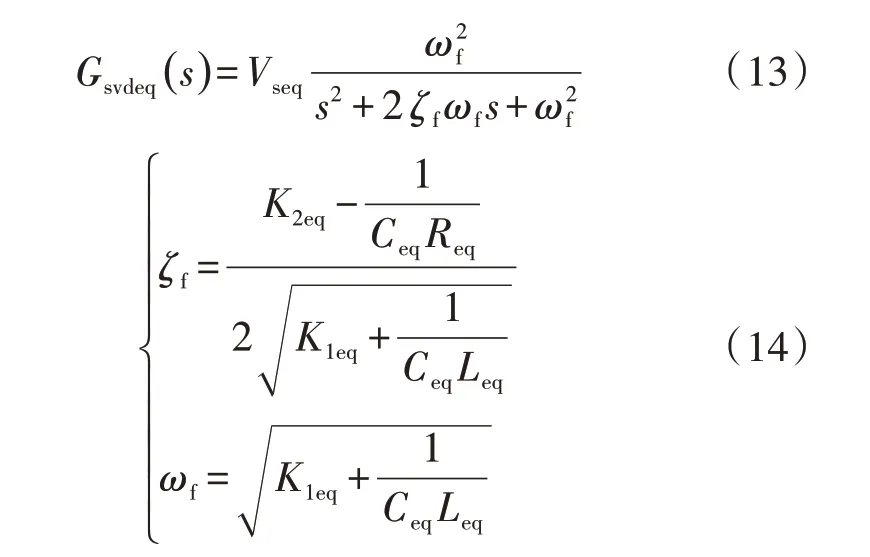
其中，ωf和ζf分别为无阻尼自然频率和阻尼比。

由式（14）可知，可调整K1eq和K2eq使得ζf为合适的正值，同时也可以改变ωf以满足系统振荡频率设计需求。

若Vsk均为相同常数值，并且假设Gsvdeq(s)等于所有Gsvdk(s)之和，则存在式（15）成立。

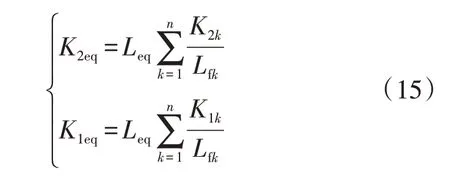
当已知各VSC 状态反馈增益时，可通过式（15）计算得到等效降阶模型的状态反馈增益，并利用传递函数Gsvdeq(s)就能够反映MVDC 配电系统中传递函数Gsvdk(s)的整体特性。

2.2 计及电压控制及下垂控制的等效降阶建模

由图4（a）可知，计及电压控制和下垂控制后，VSCk的占空比Dk(s)的表达式进一步变为：

2.3 MVDC配电系统控制参数设计方法

基于所建立的计及换流器间动态交互的开环和闭环等效降阶模型，并为达到将MVDC 配电系统控制成二阶系统（即精准设计系统振荡频率和阻尼比）的目的，本文提出了一种MVDC 配电系统控制参数设计方法，共包含如下3步。

第1 步，计算状态反馈增益。根据预设的无阻尼自然频率ωf和阻尼比ζf，计算各VSC 的状态反馈增益。

第2 步，根据各VSC 电压控制回路增益的穿越频率，设计各VSC 电压PI 控制器的比例增益和积分增益（积分增益与比例增益的比值通常为电压控制回路增益穿越频率的1/10）。为获得足够的相角裕度，电压控制回路增益的穿越频率与ωf间的比值应稍微大于1（本文取1.2），但穿越频率也应同时小于开关频率的1/10。基于所确定的穿越频率，利用所建立的计及换流器间动态交互的闭环等效降阶模型中的电压控制传递函数，就可以计算得到各VSC 电压PI控制器的比例增益和积分增益。

第3步，计算MVDC配电系统所对应二阶系统的振荡频率及阻尼比。根据式（4）、（15）和（23）计算得到等效降阶模型的滤波参数和控制参数，并通过计算电压闭环传递函数Gsivveq(s)的零、极点来确定MVDC配电系统所对应二阶系统的振荡频率和阻尼比。

3 案例分析

基于上文所介绍的等效降阶模型以及MVDC配电系统控制参数设计方法，以附录中图A5所示的MVDC 配电系统为例，开展案例分析工作。基于MVDC 配电系统的直流电压纹波V%k=1%和直流电流纹波I%k=15%标准［14］，设计电压等级为10 kV的系统，具体参数如表1 所示。在该MVDC 配电系统中，电缆线路所引入的固有振荡频率ωcz≈941 rad／s（约为150 Hz），故只要MVDC 配电系统的振荡频率ωs<188 rad／s（约为30 Hz），即当ωcz与ω0间的比值大于5倍频时，就可以忽略电缆线路的影响［16］。

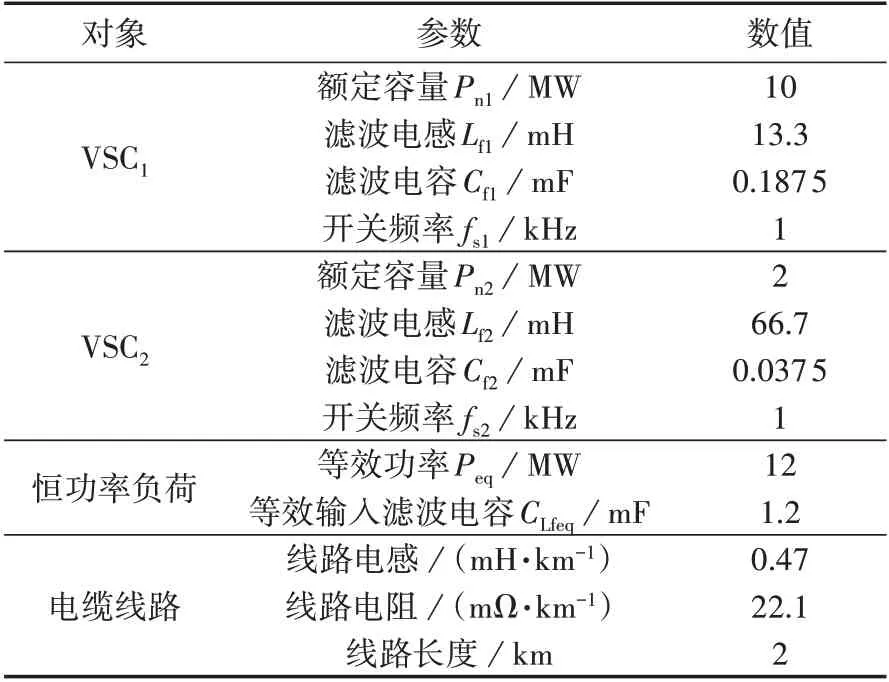
表1 MVDC配电系统参数Table 1 Parameters of MVDC distribution system

下面给出如表2 所示的7 种场景，这7 种场景的零、极点如表3 所示。表中，ff=ωf/（2π）；fs和ζs分别为系统振荡频率和阻尼比。

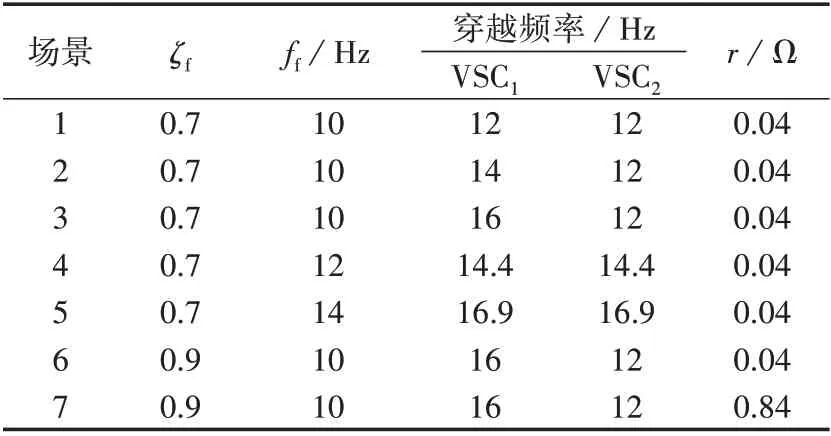
表2 场景设置Table 2 Case setting

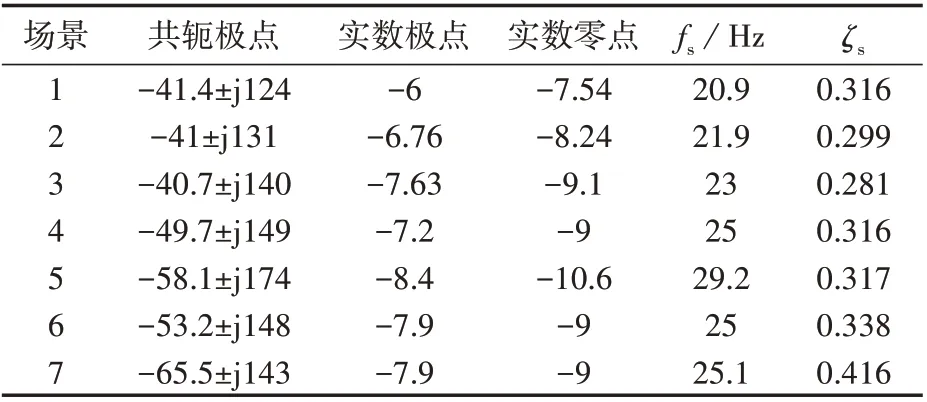
表3 等效降阶模型的零、极点Table 3 Zeros and poles of equivalent reduced-order system

由表3 可知，在场景1—7 中，由于实数零点和实数极点的相互抵消作用，MVDC 配电系统均被等效降阶为二阶系统，只是7 个场景的等效二阶系统的振荡频率和阻尼比有所差异。

3.1 MVDC配电系统等效降阶建模分析

以场景2 为例，验证所提开闭环逐步等效降阶建模方法以及MVDC配电系统控制参数设计方法的有效性。上述降阶建模过程是在忽略电缆线路影响的情况下进行的，现以表1 所示的MVDC 配电系统为例进行说明。计及电缆线路后，等效降阶模型的相关传递函数定义如下：占空比至直流母线电压的传递函数为Gvdeq_cable(s)，计及状态反馈控制后的占空比至直流母线电压的传递函数为Gsvdeq_cable(s)，电压控制回路增益为Tsvveq_cable(s)，电压闭环传递函数为Gsvveq_cable(s)。由于计及电缆线路影响的MVDC 配电系统动态特性分析不是本文的研究重点，所以本文不再提供上述4 个传递函数的表达式，笔者将在另外的文章中进行详细阐述。

场景2 下等效降阶模型的波特图如图5 所示。图中，fc和γc分别为电压控制回路增益的穿越频率和相角裕度；fb和γb分别为电压闭环传递函数的穿越频率和相角裕度。

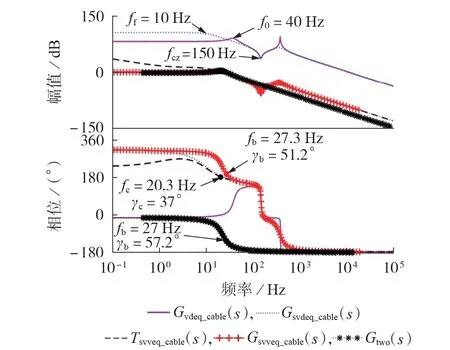
图5 场景2下等效降阶模型的波特图Fig.5 Bode diagram of equivalent reduced-order system under Case 2

下面以MVDC配电系统中各VSC动态特性存在差异的场景1—3，验证本文所提开闭环逐步等效降阶建模方法以及MVDC配电系统控制参数设计方法的有效性。传递函数Tsvv1(s)的波特图如附录中图A1 所示，传递函数Gsvveq(s)的零、极点如表3 所示。由图A1可知，增大fc会减小传递函数Tsvv1(s)的相角裕度。在场景1—3中，由于实数零点和实数极点的相互抵消作用，所以MVDC 配电系统的动态特性均可由1 对共轭极点（等效二阶系统）进行描述。并且，当增大fc时，虽然会增大等效二阶系统的振荡频率，但会减小等效二阶系统的阻尼比。

3.2 MVDC配电系统振荡频率设计及分析

3.1节的设计思路虽能调整系统振荡频率，但会改变系统阻尼比。为此，在保持fc与ff间比值不变（以1.2为例）的前提下，通过改变ff来调整系统振荡频率。以场景1、4、5 为例，画出传递函数Gvd1(s)、Tsvveq(s)的波特图如附录中图A2 所示，传递函数Gsvveq(s)的零、极点如表3 所示。由图A2 可知，增大ff会增大传递函数Tsvv1(s)的穿越频率（其相角裕度基本保持不变），并会增大等效二阶系统的振荡频率（阻尼比基本保持不变）。

3.3 MVDC配电系统阻尼比设计及分析

4 实验验证

为验证所提开闭环逐步等效降阶建模方法以及MVDC 配电系统控制参数设计方法的有效性，基于附录中图A4 所示的RT-BOX 硬件在环实验平台搭建了如附录中图A5 所示的MVDC 配电系统及等效降阶模型的开关模型。实验系统参数与理论分析参数一致，如表1所示。

4.1 MVDC配电系统等效降阶建模验证

0.1 s 时，恒功率负荷从6 MW 突增至12 MW，场景2下直流母线电压波形如图6所示。

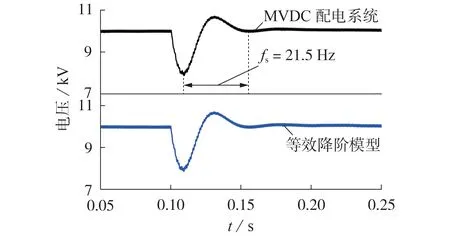
图6 验证等效降阶建模有效性的实验波形Fig.6 Experimental waveforms for verifying validity of equivalent reduced-order model

由图6 可知，MVDC 配电系统及其等效降阶模型的直流母线电压的动稳态特性具有极高的一致性，验证了本文所提开闭环逐步等效降阶建模方法的正确性和适用性。另外，图6 所示的实验结果的振荡频率约为21.5 Hz，与表3 中21.9 Hz 的理论设计值基本一致，验证了基于本文所提控制参数设计方法能够将MVDC配电系统等效降阶为二阶系统。

4.2 MVDC配电系统振荡频率实验验证

相同的实验工况下，场景1、4、5 的实验波形如附录中图A6 所示。由图可知，MVDC 配电系统及其等效降阶模型均呈现出相同的二阶系统特性，并且直流母线电压实验结果的振荡频率及阻尼比与表3中的理论设计值基本一致，验证了通过改变ff来设计系统振荡频率的合理性。

4.3 MVDC配电系统阻尼比实验验证

相同的实验工况下，场景3、6、7 的实验波形如附录中图A7 所示。由图可知，MVDC 配电系统及其等效降阶模型均呈现出相同的二阶系统特性，且场景3、6、7 的直流母线电压超调量逐渐减小，表明MVDC 配电系统阻尼比逐渐增大，验证了通过增大ζf和r来增大系统阻尼的有效性。

相同的实验工况下，场景7下2台VSC的输出电流波形如图7 所示。由图可知，VSC1和VSC2的实际输出电流大小比值为5（与额定容量比值一致），验证了下垂控制的有效性。综上所述，状态反馈控制及电压控制能够实现系统动态调整，而下垂控制能够完成稳态功率分配。

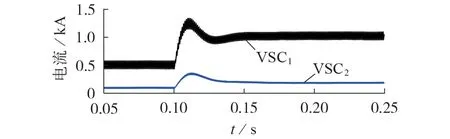
图7 VSC1和VSC2的输出电流波形Fig.7 Waveforms of output current of VSC1 and VSC2

5 结论

本文针对MVDC 配电系统等效降阶建模及控制参数设计开展了相关研究，得到结论如下。

（1）基于所提出的开闭环逐步等效降阶建模方法，建立了计及换流器间动态交互的开环和闭环等效降阶模型，并建立了MVDC 配电系统及其等效降阶模型间相应参数（滤波参数、状态反馈控制参数和电压控制参数）的通用关系表达式。基于等效降阶建模方法所建立的等效降阶模型的阶数，不会受到MVDC 配电系统中VSC 的台数、滤波参数及控制参数差异性的影响。

（2）基于计及换流器间动态交互的开环和闭环等效降阶模型，并利用状态反馈控制方法以及所提出的MVDC 配电系统控制参数设计方法，在多个场景下均能够将MVDC配电系统控制成二阶系统。无论各个VSC 的滤波参数以及控制参数是否一致，当等效降阶模型的电压闭环传递函数频域曲线呈现出典型二阶系统特性时，基于此二阶系统所计算得到的振荡频率和阻尼比就能够精确反映出MVDC配电系统的硬件在环时域实验结果。由多个场景的硬件在环实验结果可知，MVDC 配电系统及其等效降阶模型的直流母线电压动稳态特性具有高度的一致性。

附录见本刊网络版（http：//www.epae.cn）。