陶粒混杂纤维混凝土强度正交试验研究
沈恒祥,孔 云,庞建勇
(安徽理工大学 土木建筑学院,安徽 淮南 232000)
1 研究背景
随着人口密度的逐渐提高,我国建筑物逐渐向高层与大跨度的方向发展,建筑物的自重随之提高。据研究,轻质高强混凝土的使用可降低钢筋混凝土40%左右的自重[1]。陶粒混凝土虽然能有效地降低建筑物自重,但毕建静和高震[2]发现陶粒混凝土本身的力学性能相对于普通混凝土有着明显的不足。另外,邵永健等[3]的研究表明,陶粒混凝土砌块的抗剪强度最大值出现在轴压比为0.5左右时,比普通混凝土提前0.1左右,在陶粒混凝土未发生脆性破坏的时候,先发生剪切破坏;班永周[4]认为较低弹性模量的轻骨料会导致混凝土的弹性模量较低,且抗剪能力较弱。
针对上述问题,一些专家及学者开展了相关研究,研究结果表明在轻骨料混凝土中掺入一定量的混杂纤维能够提高混凝土的力学性能[5-7]。周航等[8]指出玄武岩纤维具有优越的力学性能,并且与混凝土具有天然的相容性;张兰芳等[9]、阮明和和刘宏伟[10]的试验表明随着玄武岩纤维掺量的增加,混凝土的抗压强度逐渐增强,并且混凝土的脆性逐渐降低。其他一些研究也表明在轻骨料混凝土中掺入聚丙烯纤维,有助于提高轻骨料混凝土的抗压强度并改善其脆性[11-14]。已有研究表明将玄武岩纤维与聚丙烯纤维掺入混凝土能提高轻骨料混凝土的力学性能,但需有待开展进一步系统的量化研究。
本文对陶粒、玄武岩纤维和聚丙烯纤维进行三因素三水平的正交试验,研究其对混凝土抗压强度及最大抗剪强度的影响,对于解决目前轻质混凝土力学性能不足的问题具有一定的参考和借鉴意义。
2 试验材料与设计
2.1 原材料
玄武岩纤维采用的是平均长度15 mm、单丝直径为12.2 μm的短切玄武岩纤维,其物理力学性能如表1所示。

表1 玄武岩纤维物理及力学性能
试验所用的水泥为淮南八公山牌PO 42.5级普通硅酸水泥,砂子为普通中砂,细度模数为2.8,并在其中掺杂最大粒径5 mm、表观密度2 543 kg/m3的陶砂,其目的是减少混凝土重度,并增加混凝土抗酸雨、保温隔热的能力。所选石子为最大粒径<15 mm的卵石,以满足混凝土的流动性,并使用陶粒代替部分卵石来减少混凝土的重度并增加混凝土保气隔水的能力。陶粒粒径大小为5~20 mm,为页岩陶粒,由淮南市金瑞建材厂生产,其松散密度为600 kg/m3,筒压强度为3 MPa,孔隙率>37%,吸水率<16%。玻化微珠密度为100 kg/m3,闭孔率>85%,成球率60%~80%,粒径0.15~0.5 mm,吸水率约200 %。由于玻化微珠吸水率过高,在使用前需进行淋水处理,防止在搅拌混凝土时过度吸水。粉煤灰采用淮南某电厂生产的一级粉煤灰,其作用是节省水泥和细骨料用量,降低用水量,增强混凝土拌和物的和易性,减少混凝土的徐变和提高混凝土抗渗能力。为了提高早期混凝土强度,使用聚羧酸高性能减水剂作为外加剂。
聚丙烯纤维采用山东泰安市现代塑料有限公司开发生产的束状单丝聚丙烯纤维。其物理力学性能如表2所示。

表2 束状单丝聚丙烯纤维物理及力学性能
2.2 试验设计
参考混凝土设计规范,本试验中基准混凝土的水泥、砂子、石子、水配比取为1∶1.75∶1.75∶0.45。正交试验是安排多因素多水平试验的一种有效方法,其原理是根据正交性从全面试验中挑出有代表性、典型性的点进行分析,以达到高效、快速和经济的目的[15]。本次试验主要考虑因素为:①陶粒掺量Af(7%、14%、21%),对应因素水平为A1、A2、A3;②玄武岩纤维掺量Bg(0.1%、0.2%、0.3%),对应因素水平为B1、B2、B3;③聚丙烯纤维掺量Cv(0.1%、0.2%、0.3%),对应因素水平为C1、C2、C3。按照正交试验的要求取用9组配合比,进行三因素三水平的设计,1 m3混凝土配比如表3所示。
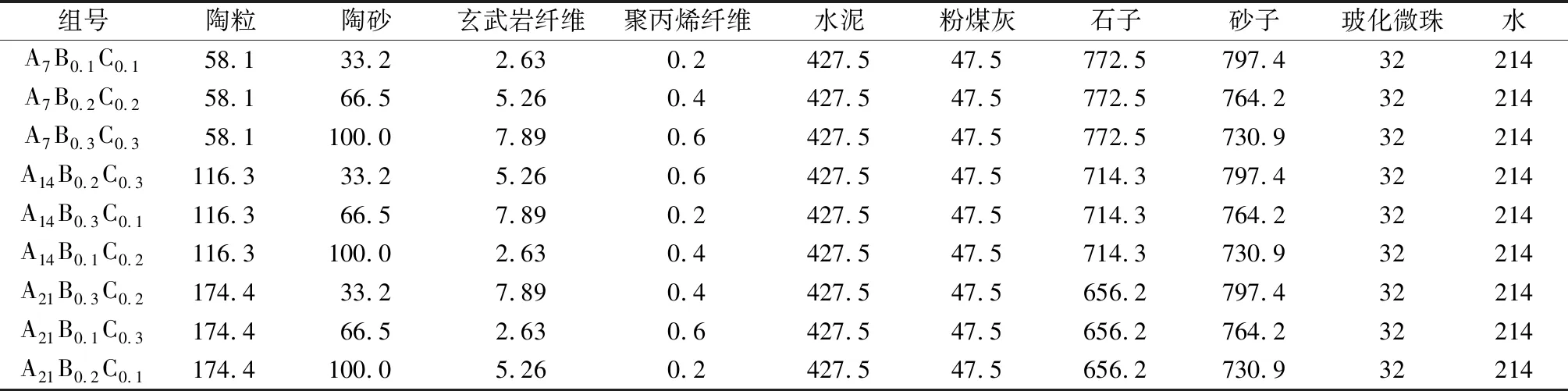
表3 混凝土配比
2.3 试块制备
按照试验规范,首先加入砂石与各种胶材对其进行干拌,然后加入水和减水剂,同时均匀地撒入纤维进行湿拌。每组配合比制备3块边长100 mm的标准立方体试件用于抗压强度试验,同时每组制备3块边长50 mm的标准立方体试件用于测试其最大抗剪荷载。
3 试验结果与分析
将试块按照试验规范要求养护28 d后进行强度试验,测得其抗压强度与最大抗剪荷载如表4所示。为了探究陶粒、玄武岩纤维和聚丙烯纤维对于混凝土抗压强度与最大抗剪荷载的影响,利用统计分析软件SPSS对其进行极差计算和方差分析。

表4 抗压强度与最大抗剪荷载
3.1 极差分析
由表5、图1可知,陶粒掺量对混杂纤维混凝土的抗压强度影响最大,极差R为5.00 MPa;玄武岩纤维次之,极差R为2.27 MPa;聚丙烯纤维对混杂纤维混凝土抗压强度的影响最小,极差R为1.53 MPa。Af从7%增长到14%,其抗压强度降低了14.3%;Af从7%增长到21%,其抗压强度降低了18.3%。这是由于陶粒代替了部分石子作为粗骨料,而陶粒本身是疏松多孔的结构,在减轻混凝土自重的同时也降低了混凝土本身的抗压强度。Bg从0.1%增大到0.2%,其抗压强度增大了4.4%;Bg从0.1%增大到0.3%,其抗压强度增大了9.7%。Cv从0.1%增大到0.2%,其抗压强度减少了0.7%;Cv从0.1%增大到0.3%,其抗压强度增大了5.7%。陶粒掺量对混杂纤维混凝土有明显的反向影响;玄武岩纤维掺量与聚丙烯纤维掺量对于混杂纤维混凝土的抗压强度都有较为明显的正向影响。

表5 抗压、抗剪荷载极差分析

图1 28 d抗压强度效应曲线
由图2、表5数据可知,玄武岩纤维对混杂纤维混凝土的最大抗剪荷载影响最大,极差R为17.40 kN;陶粒其次,极差R为11.27 kN;聚丙烯纤维对最大抗剪荷载的影响最小,极差R为6.83 kN。Bg从0.1%增长到0.2%,其最大抗剪荷载增长了17.6%;Bg从0.1%增长到0.3%,其最大抗剪荷载增长了36.2%。Cv从0.1%增长到0.2%,其最大抗剪荷载增长了11.9%;Cv从0.1%增长到0.3%,其最大抗剪荷载增长了13.1%。这是由于玄武岩纤维与聚丙烯纤维本身就有一定的弹性模量并具有良好的抗剪能力,在混凝土结构中交织组成纤维网状结构,能有效地提高混凝土的抗剪能力。Af从7%增长到14%,其最大抗剪荷载降低了6.7%;Af从7%增长到21%,其最大抗剪荷载增高了13.7%。可见随玄武岩纤维掺量与聚丙烯纤维掺量的增加,混杂混凝土的抗剪荷载在增加。

图2 28 d最大抗剪荷载效应曲线
3.2 方差分析
如表6所示,通过方差分析可知,各因素对28 d混杂纤维混凝土的抗压强度的影响顺序为:陶粒>玄武岩纤维>聚丙烯纤维。此结果与极差分析结果一致,其中陶粒掺量对抗压强度的影响为高度显著,而玄武岩纤维掺量和聚丙烯纤维掺量对于抗压强度的影响为显著。再根据主成分分析法分析各因素的相关性可知,陶粒掺量与混杂纤维混凝土抗压强度的相关性最大,相关系数为-0.833;玄武岩纤维次之,相关系数为0.373;聚丙烯纤维最小,相关系数为0.228。随着玄武岩纤维掺量和聚丙烯纤维掺量的增加,混杂纤维混凝土的抗压强度有所提高,其相关系数分析结果与方差分析结果一致。
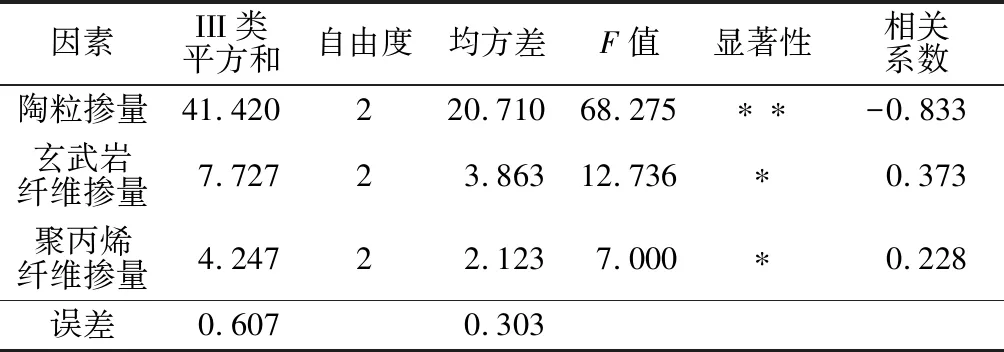
表6 28 d抗压强度方差分析与各因素相关性分析
由表7可知,根据方差分析得到的混杂纤维混凝土的最大抗剪荷载影响结果与极差分析一致,即玄武岩纤维>陶粒>聚丙烯纤维。其中玄武岩纤维对于最大抗剪荷载的影响为高度显著,陶粒与聚丙烯纤维对于最大抗剪荷载的影响为显著。由主成分分析法可知玄武岩纤维掺量与混杂纤维混凝土抗压强度的相关性最大,相关系数为0.778;陶粒其次,相关系数为0.335;聚丙烯纤维最小,相关系数为0.302。玄武岩纤维、陶粒、聚丙烯纤维的相关性分析与方差分析结果均相同。
4 强度模型的建立与检测
4.1 抗压强度预测模型的建立
利用SPSS软件的多元线性回归模块对混杂纤维混凝土的抗压强度进行回归分析,采用后退分析法并以陶粒掺量、玄武岩纤维掺量和聚丙烯纤维掺量3种因素作为影响混杂纤维混凝土抗压强度的影响因素。

表7 最大抗剪荷载方差分析与各因素相关性分析
由前述可知,对于混杂纤维混凝土的抗压强度影响为高度显著的因素为陶粒掺量,显著因素为玄武岩纤维掺量和聚丙烯纤维掺量,根据复合材料力学理论,将陶粒纤维混凝土看作基体相,玄武岩纤维相和聚丙烯纤维相作为组成三相基体复合材料[16]。所以,在混杂纤维混凝土的抗压强度包含陶粒增强项、玄武岩纤维增强项、聚丙烯纤维增强项和基体相(常量)这4个部分。这4部分的模型系数以及模型系数的检验如表8所示,其中X为模型中Af、Bg、Cv、m(常量)前的系数。

表8 各因素的模型系数及检验结果
根据表8中显著性的分析,模型1中陶粒掺量的显著性水平明显低于模型2和模型3,因而选择-0.357作为陶粒掺量这一因素的模型系数。同理可得,玄武岩纤维掺量和聚丙烯纤维掺量的模型系数分别为11.727和8.788。常数项m则选择模型1中的常量。最终得到抗压强度fcu的预测模型,即
fcu=25.427-0.357Af+11.727Bg+8.788Cv,
R2=0.94 。
(1)
4.2 最大抗剪荷载预测模型的建立
基于复合材料理论,利用SPSS软件的多元线性回归功能,建立混杂纤维混凝土的最大抗剪荷载的预测模型,系数的选取与抗压强度预测模型的系数选取一致。以此为基础得到最大抗剪荷载fv预测模型,即
fv=22.430+0.54Af+89.215Bg+49.036Cv,
R2=0.96 。
(2)
陶粒混杂纤维混凝土的抗压强度以及最大抗剪荷载的试验值与预测值如表9所示,其中抗压强度的试验值与预测值的相对误差保持在6.2%以内,说明抗压强度预测模型具有良好的精度。虽然最大抗剪荷载模型预测在第2组、第4组和第6组的相对误差的绝对值>9%,但最大抗剪荷载预测模型的平均相对误差为2.2%,证明预测模型具有较好的精度。部分组相对误差较大的原因如图2所示,虽然陶粒掺量对于混杂纤维混凝土的最大抗剪荷载的影响较为显著,但表现得极不规律,这就是最大抗剪荷载预测模型产生较大误差的原因。
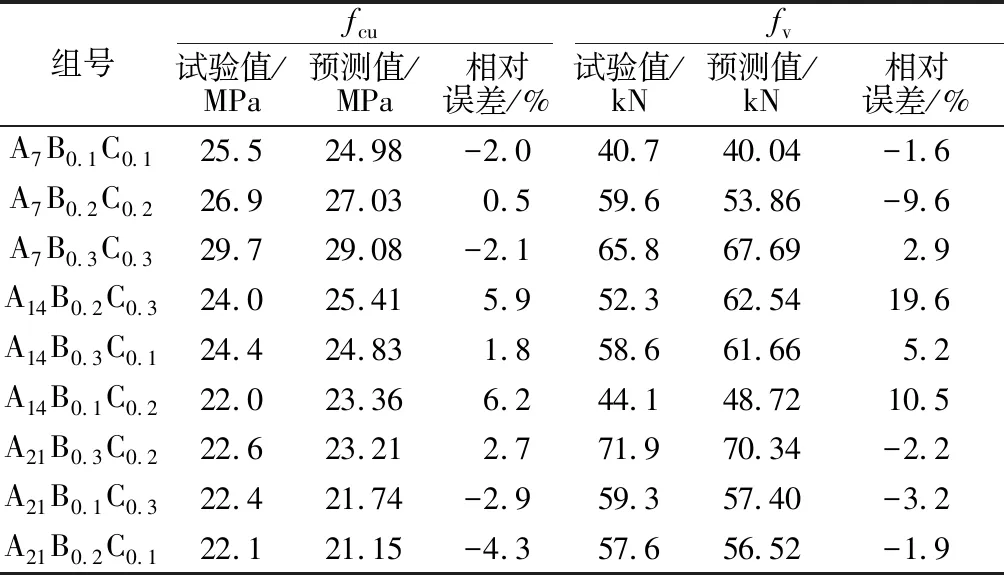
表9 混杂纤维混凝土抗压强度及最大抗剪荷载的实测值、预测值和相对误差
5 结 论
本文通过玄武岩-聚丙烯混杂纤维混凝土力学性能的正交试验研究,得出如下结论:
(1)陶粒掺量、玄武岩纤维掺量和聚丙烯纤维掺量对于混杂纤维混凝土的抗压强度和最大抗剪荷载都有着显著影响。通过极差分析得到对于抗压强度的影响顺序为:陶粒掺量>玄武岩纤维掺量>聚丙烯纤维掺量;对于最大抗剪荷载的影响顺序为:玄武岩纤维掺量>陶粒掺量>聚丙烯纤维掺量。
(2)当陶粒掺量从7%增长到21%时,混杂纤维混凝土的抗压强度降低了18.3%,说明陶粒掺量与混杂纤维混凝土抗压强度之间表现出负相关性。
(3)通过方差分析可知,陶粒掺量、玄武岩纤维和聚丙烯纤维掺量对于混杂纤维混凝土的抗压强度与最大抗剪荷载有显著性的影响,特别是陶粒掺量在抗压强度上具有高度显著性影响,玄武岩纤维在最大抗剪荷载上具有高度显著性影响;同时玄武岩纤维和聚丙烯纤维在对混杂纤维混凝土强度的影响中表现出正相关性,在混杂纤维混凝土中掺杂玄武岩纤维能有效提高其抗剪荷载性能,掺杂玄武岩纤维和聚丙烯纤维能有效地提高陶粒混杂纤维混凝土的抗压强度。
(4)建立的关于混杂纤维混凝土抗压强度及最大抗剪荷载的预测模型能够精确地预测其抗压强度以及最大抗剪荷载,对混杂纤维混凝土的力学性能研究具有一定的参考意义。

