基于动态贝叶斯网络的混凝土坝失事风险分析

李宗坤，王 特，葛 巍,3，郑 艳

(1. 郑州大学 水利科学与工程学院， 郑州 450001；2. 郑州大学 软件学院， 郑州 450002;3. 代尔夫特理工大学 技术、政策和管理学院，荷兰 代尔夫特 2628 BX)

1 研究背景

混凝土坝在长期服役过程中，发挥巨大工程效益的同时，必然存在一定的风险。虽然混凝土坝失事的发生机率很小，但其溃决模式多为瞬间溃坝，应急时间较短，一旦溃决失事，不仅大坝损毁，还会给下游带来重大灾难[1-2]。20世纪曾经发生过3次震惊世界的混凝土坝失事事件, 分别为1928年的美国圣弗朗西斯 (St.Francis) 重力坝溃决、1959年法国马尔帕塞 (Malpasset) 拱坝溃决和1963年意大利瓦依昂 (Vajont) 拱坝失事[3]，均对人类生命和社会经济造成了不可估量的损失。因此，对混凝土坝进行科学合理的风险分析和管理显得尤为重要。

目前关于混凝土坝失事风险方面的研究已较为广泛，其安全管理理念也逐渐由传统的工程安全管理向风险管理转变。如顾冲时等[2]论述了混凝土坝长效服役与风险评定理论、方法及其技术的研究现状；姚霄雯等[4]总结了混凝土坝的溃坝特点和主要溃坝原因；聂学军[5]结合事件树法和专家经验进行了混凝土坝溃坝概率计算和风险决策探讨。这些研究在实际工程中均具有一定的指导意义，但仍缺乏对系统风险源进行深入性的分层分级归纳，且在定量计算时对风险因素的不确定性和时变性考虑较少。传统的溃坝风险概率分析方法，如层次分析法[6]、事件树分析法[7]、故障树分析法[8]等，在解决不确定性问题方面并不理想。此外，这些方法均没有很好地解决各级事件之间的关联性问题，而实际工程中上下级事件往往存在着一定的相关性，必须予以充分考虑并进行具体分析。

贝叶斯网络(Bayesian Network, BN)[9-11]是一种应用于不确定性知识表示和推理的方法，能够很好地弥补以上方法的不足，由以色列科学家Pearl于1988年提出。随着贝叶斯理论的不断发展和深入，其实际应用范围也越来越广，近年来在水利工程风险分析和评估领域也得到了应用[10,12-13]，但大多数研究中构建的贝叶斯网络都是静态的，未将时间因素考虑在内，在实际运用中存在一定的局限性。混凝土坝在长期服役过程中，风险因素的状态随时间呈动态变化，各风险因素在各个时间段内的发生概率往往不同。

本文通过构建动态贝叶斯网络(Dynamic Bayesian Network, DBN)模型，旨在较清晰地反映出混凝土坝各风险因素发生概率的时序变化特征和发展趋势，以提高风险评估的合理性，从而为管理部门风险管控措施的制定提供科学依据。

2 混凝土坝失事风险因素分析

风险识别是大坝风险分析与管理的基础，更是风险评价和风险处理的前提[14-15]。对混凝土坝进行失事风险评估，首先应对可能导致失事的风险因素进行科学的辨识和分类，为后续系统性的分析和定量计算拟定框架。

根据国内外混凝土坝失事统计资料[4-5,16]可知，洪水漫顶、结构失稳、坝基破坏以及坝体破坏是导致其失事的主要原因。其中，洪水漫顶会对下游面坝体、坝趾以及厂房等设施造成巨大冲击破坏。漫顶的洪水包括自然降雨以及因风暴、滑坡、地震等自然灾害引起的壅浪[17]。此外，泄水建筑物泄流能力不足也是引起洪水漫顶的重要原因，如闸门故障、溢洪道泄流能力不足等，导致上游洪水不能及时下泄而发生漫顶。

结构失稳通常与抗滑能力不足和承受异常荷载有关。超标准洪水不能及时下泄、淤泥层清理不彻底、地基防渗处理不当或排水设备缺陷等，都会导致大坝抗滑能力大大降低；异常荷载如地震、上游山体滑坡等，通常直接引起坝体结构沿薄弱面滑动或坝体倾覆。

坝基破坏被认为是混凝土坝失事的最主要原因[4]。引起坝基破坏的原因主要有2方面：一是地基原始缺陷或施工处理不当；二是混凝土坝内部防渗体系设计不当或排水设备缺陷，渗透水流沿坝基和坝肩处裂隙或断层持续渗漏，造成坝基滑动破坏。

坝体破坏主要是由坝体防渗不当和材料质量恶化引起的，包括大坝在长期运行过程中受服役环境的影响而产生的风化侵蚀、碱骨料反应、冻融腐蚀等等，导致材料强度降低。

根据以上分析，可将混凝土坝失事风险主要指标归纳如下，如表1所示。

表1 混凝土坝失事风险指标

3 DBN风险评估模型的构建

3.1 静态贝叶斯网络模型

贝叶斯网络(Bayesian Network，BN)又称信念网络，是用来表达和计算随机变量间概率关系的有向无环图[11-12]，适用于解决不确定性和不完整性问题。其主要由父节点、子节点，以及表达各节点之间关系的箭头构成。如图1所示，节点A、B为节点C的父节点，节点C为节点A、B的子节点。

贝叶斯网络的理论依据是贝叶斯公式和全概率公式，如式(1)和式(2)所示。

图1 贝叶斯网络示意图

(1)

(2)

式中：P(B)为事件B的概率，称为先验概率；P(B|A)为事件A已发生的条件下，事件B发生的条件概率；P(A|Bi)称为似然率；n为事件个数；P(Bi)为事件Bi的概率。

一个贝叶斯网络的运行结果即为所研究的问题中所有变量的联合概率分布，即考虑所有因素影响下的概率值。图1中简单贝叶斯网络的联合概率分布如式(3)所示。

P(A,B,C)=P(C|A,B)P(A,B)=

P(C|A,B)P(A)P(B) 。

(3)

式中：P(A,B,C)为事件A、B、C的联合概率；P(A,B)为事件A、B的联合概率；P(C|A,B)为事件A、B已发生的条件下，事件C发生的条件概率。

节点的先验概率状态只有“发生”和“不发生”2种状态；子节点的条件概率状态与父节点个数有关，每个父节点都有“发生”和“不发生”2种状态，故子节点的条件概率共有2n种状态。如图1中C节点发生的条件概率共有4种，分别为“A、B都不发生”“A发生、B不发生”“B发生、A不发生”及“A、B都发生”。由此可知，若已知各父节点的先验概率及相应条件概率分布，则可以得到包含所有节点的联合概率分布。用来反映父节点与子节点关联性的条件概率可通过样本学习或专家经验给定[18-19]。

3.2 动态贝叶斯网络模型

随着各风险事件的发展，不同时间节点下同一事件发生的概率往往不同。考虑工程实际，在此引入时间因素，实现静态贝叶斯网络向动态贝叶斯网络(DBN)的过渡。鉴于动态系统的复杂性，目前大多数研究成果都是在一定假设的基础上，对动态模型进行简化处理，常用的假设有马尔可夫假设和转移概率不变假设等[20-21]。

基于上述2个假设，DBN模型的建立可分为两部分：一是建立先验网络B0，并定义初始时刻的联合概率分布PB0(X)；二是建立转移网络B→，并根据相应的工程阶段或实际分析的需要，将整个过程划分为若干个时间段(又称为时间片)，定义同一事件在相邻时间片上的转移概率P(X[t+1]/X[t])。在初始时刻，事件X[1]的父节点是先验网络B0中的节点；在t+1时刻(t>0)，事件X[t+1]的父节点为转移网络B→中的节点，且此节点与时刻t和时刻t+1均有关，见图2。DBN网络中事件X在T个时间片上的联合概率分布P(X[1],X[2],…,X[T])如式(4)所示。

P(X[1],X[2],…,X[T])=

(4)

图2 DBN构成

(5)

根据转移概率不变假设，同一事件在相邻2个时间片上的转移概率都是相同的，但考虑到溃坝模型中各个事件的模糊性和不确定性，这种概率无法通过样本统计学习的方法得到，只能在充分参考相关资料的基础上，由水利工程专家拟定[19]。

3.3 条件概率的拟定

由于人类对风险的辨识存在一定的局限性，在实际运用中，总会有一些未知或遗漏的因素对贝叶斯网络中的节点产生影响。为充分考虑各种因素对节点的影响，Henrion 提出了遗漏概率(Leak Probability)的概念，并给出了Leaky Noisy-or gate扩展模型[22]， 以提高概率计算的客观性。

P(X|Xm)Pm+Pn-PmPn;

(7)

(8)

两式联立，可得

(9)

将各事件父节点中所有未考虑到的因素综合为一个未知因素Xl，设其连接概率为Pl，则节点X的条件概率为

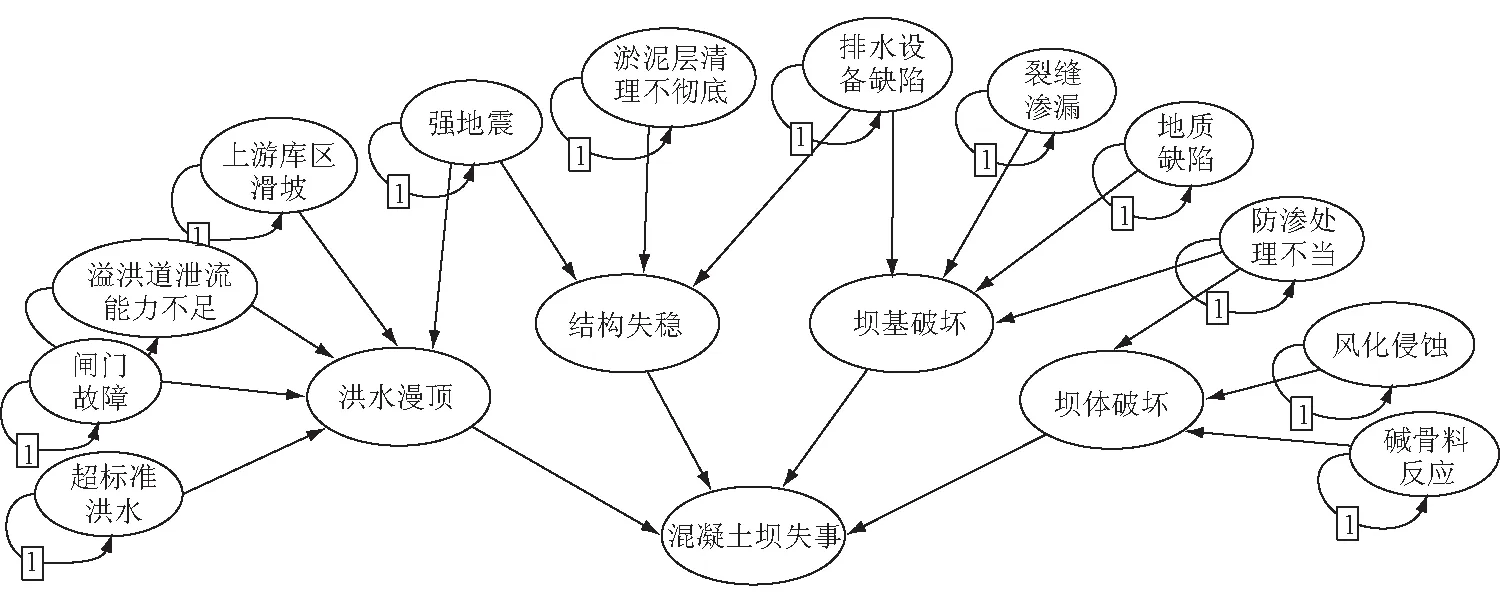
图4 混凝土坝失事DBN模型

4 混凝土坝失事风险概率评估

4.1 混凝土坝失事风险概率评估模型

作为一款专门用于图形决策理论模型构建和分析计算的建模工具[23]，本研究采用GeNIe软件构建风险概率评估模型和数据推理。

将基本数据输入GeNIe软件所构建的贝叶斯网络之中，进行动态贝叶斯网络推理，并选取关键时间节点的先验概率进行实时更新。通过机器学习对动态推理结果进行修正和整合，实现数学理论和专家知识的相互补充，从而进一步提高评估结果的科学性与合理性，其流程如图3所示。

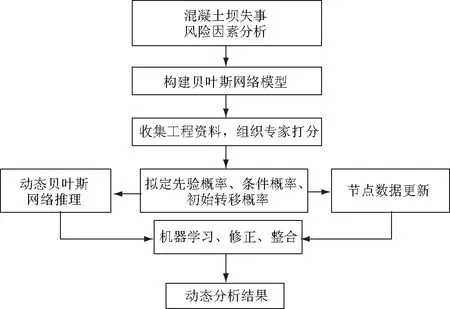
图3 混凝土坝失事风险评估流程

根据表1中所确定的风险指标及风险因素与风险事件间的因果关系，构造如图4所示的动态贝叶斯网络模型。其中，各风险因素作为基本指标，对应贝叶斯网络中最上层的父节点；“混凝土坝失事”作为推理分析的末端，表示为最终节点。各指标之间的关联性由带指向的箭头来反映；各父节点上的有向圆弧段“1”表示相邻时间片的时间间隔为1[10]。

4.2 指标分析

由于水利工程失事的特殊性和不可复制性，且大量的事故相关数据难以获得，故在此采用专家调研打分[14,24]的方式来确定指标概率。该方法既避免了单纯依赖历史资料统计所带来的巨大偏差，又可将专家群体的知识和经验与实际工程相结合，达到具体问题具体分析的目的，从而提高评估结果的可靠性。

为统一专家打分时的概率表述，并使打分数据易于参考和区分，在此采用联合国政府间气候变化专门委员会(Intergovernmental Panel on Climate Change，IPCC)提出的7级风险概率表述方式[25]。考虑到溃坝概率的一般范围是10-5～10-4[14]，故将此概率表中所有取值都乘以10-4，其概率范围及对应语言表述见表2。此外，为减小不同专家估值带来的主观性差异，对于评估差异较大的项，应重新组织专家充分论证并重新估值，直至所有专家的评估值均处于表2中同一区间或相邻区间为止。

表2 基于IPCC的概率定性表述

5 实例分析

5.1 工程概况

某水库总库容2 700万m3，枢纽工程主要包括拦河坝、引水系统和发电厂房。拦河坝为碾压混凝土重力坝，最大坝高56.8 m，坝顶长122.5 m，坝顶宽5.0 m，上游面垂直，下游坡度1∶0.75，采用坝体表孔溢流，溢流坝段长37.0 m，布置3孔，单孔尺寸为10.0 m×6.0 m(宽×高)；左侧挡水坝段长48.0 m，右侧挡水坝段长37.5 m。

表5 动态推理结果

5.2 先验概率及条件概率的获取

以人工干预(不定期除险加固)条件下的此水库为研究对象，在充分研究工程资料的基础上，组织水利工程专家对DBN模型中各节点的先验概率、条件概率及原始转移概率进行估值, 并运用Leaky Noisy-or gate扩展模型，将未知因素考虑在内，进一步提高条件概率的准确性。限于文章篇幅，仅以DBN模型中“坝体破坏”节点概率计算为例进行说明。

设“坝体破坏”为事件X，其代表性父节点“防渗处理不当”“风化侵蚀”“碱骨料反应”分别为X1、X2、X3，“Xi=1”表示该事件发生，“Xi=0”表示该事件不发生。P(Xit)表示事件i的原始转移概率，在此可理解为事件i于前一时间片已发生的前提下，在当前时间片仍然发生的概率。

通过专家对各个事件状态概率进行打分，得到事件X各父节点的先验概率、条件概率及原始转移概率，如表3所示。

表3 节点X(坝体破坏)概率参数

设未知因素为Xu，令P(Xu=1)=0.1,代入式(7)和式(8)，可得节点X的条件概率，如表4所示。

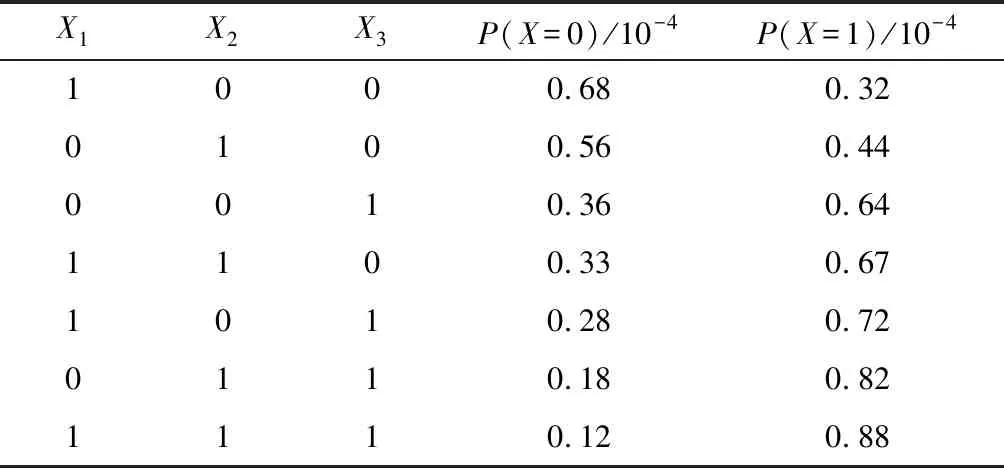
表4 节点X(坝体破坏)条件概率

5.3 DBN推理

按照5.2节中各个因素先验概率和条件概率的确定方法，依次求出各个节点的状态概率，输入DBN推理模型，将时间片数量设定为10，并对关键时间节点的先验概率进行更新。运行软件完成不同时间片下溃坝事故的动态推理过程，各节点动态推理结果如表5所示。

混凝土坝失事风险概率时序变化曲线如图5(a)所示；4类风险事件的概率时序变化曲线如图5(b)所示。各风险因素概率时序变化曲线如图6所示。

图5 失事风险及各风险事件概率时序变化曲线

图6 各风险因素概率时序变化曲线

5.4 对比分析

为验证DBN推理的正确性，可将其推理结果与相应的静态贝叶斯网络推理结果进行对比分析。取后5个时间片的溃坝风险评估为例，用GeNIe软件得到的静态贝叶斯网络推理结果如表6所示。

表6 静态贝叶斯网络推理结果

将表6中数据与DBN推理结果进行比较，可以发现2种方法的推理结果较为吻合。对于后5个时间片，动态贝叶斯网络推理结果相对略低，这是因为DBN模型能够对前一时刻的推理结果进行有效的积累并反馈于新的时间节点。与静态贝叶斯网络不同，动态贝叶斯网络评估模型能够根据现有时刻的状态信息对其它时刻的状态进行推理并反馈于整个时间过程，使数学推理与专家经验达到有效结合。因此，该模型在实际运用中不会因某一时刻数据的缺失或失真而使评估结果出现较大偏差。此外，静态贝叶斯网络模型需要逐次对所有时间片的先验概率进行评估并输入，工作量大且计算繁琐，而动态贝叶斯网络模型在便捷性方面具有明显优势，且随着各节点信息的补充和完善，评估结果会更加准确可靠。

5.5 失事风险概率评估

由图5(a)可知，该混凝土坝失事风险概率总体上趋于平稳变化，节点概率大多处于0.33×10-4以下，对应于表2可知，其失事可能性较小，总体上处于可控状态。其中，第6个时间片内的失事概率最大，达到了“中等可能发生”。由图5(b)和图6可知，这是因为该时间片内坝基破坏、裂缝渗漏及防渗措施不当等风险因素发生的概率较大。考虑到溃坝事故的特殊性和溃坝后果的严重性，这种状态即意味着大坝的状况已不能满足安全运行的需要，必须通过管理部门的除险加固来降低失事风险，并启动相应的预警机制，以防重大事故的发生。

图5(b)还反映出，相对于其他3类风险事件，“坝基破坏”的发生概率更高，时序变化曲线波动性更大，表明此类风险事件的易发性和不稳定性，应在实际工程中特别注意对这类风险事件的防范。从图6可以观察到，在各一级指标中，“裂缝渗漏”和“防渗处理不当”在时间轴上呈现较强的波动性，表明转移概率对这两类风险因素的影响更大，随时间变化更为明显，需在此后的工作中特别加强对此类隐患的监控和定期排查，并做好预警和应急工作，防患于未然。

6 结 论

混凝土坝运行期风险因素具有不确定性，且随时间呈动态变化。本文通过引入时间因素，构建了基于动态贝叶斯网络的混凝土坝失事风险概率评估模型。运用该模型对某混凝土坝进行失事风险概率评估，结果表明该坝失事的可能性较小，并在第6个时间片内达到最大，罗列出了风险波动较大的因素。

相比于其他风险分析方法，该方法不会因某时间节点上的信息缺失或失真而使最终结果产生巨大偏差，为同类工程动态风险分析和评估提供了一种新的思路。鉴于该评估模型的构建基于转移概率不变的假设，此方法较适用于风险因素转移概率随时间变化相同或相近时的动态评估。

先验概率及转移概率的确定在该模型中具有重要意义，下一步将考虑与可靠度等方法相结合来确定概率，进一步提高该模型评估的准确性。