水位变化速率对河道崩岸的影响

吕庆标，岳红艳，朱勇辉，李凌云

(长江科学院 河流研究所，武汉 430010)

1 研究背景

在冲积平原河流中，崩岸是河道横向演变的重要表现形式。崩岸现象的频繁发生，将严重威胁江河堤防安全、河势稳定、航运发展和沿岸基础设施安全，并造成河道两岸土地大量丧失等[1]。三峡水库的蓄水运用改变了长江中下游河道的水沙条件，由于来沙量大幅度减少，河道由冲淤总体基本平衡转化为长时期长距离的冲刷[2]，长江中下游河道崩岸面临新的严峻形势。虽然两岸护岸工程对河势稳定起到了积极作用，长江中下游河道河势总体较为稳定，但受水流顶冲点上提或下挫的影响，部分未护河段及失去防护作用的已护岸段河势调整剧烈，仍常有崩岸发生[3]。仅2003—2018年十多年间共发生崩岸险情946处，累计崩岸长度约704 km。同时，水库的调度改变了坝下游河道的水位、流量过程，而水位的涨落与河岸的稳定和崩岸的发生息息相关。水库蓄水期减小出库流量，导致下游河道短时期内水位变幅较天然时期大，对岸坡稳定产生一定不利影响。因而，有必要研究水位变化速率对河岸崩塌的影响，所得成果对防灾减灾具有重要意义，同时也可为三峡水库科学调度提供科技支撑。以往对于崩岸问题的研究，国内外学者多从影响因素着手，借助的研究方法包括理论分析、数值计算及概化模型试验等。

吴玉华等[4]通过分析马湖堤崩岸，认为马湖堤崩岸是水流冲刷作用、水位降落速率较快、河岸自身稳定性较差等因素共同作用的结果。王永[5]认为水流冲刷作用是长江安徽河段崩岸的主要因素，其次是河岸地质条件和渗流作用。余文畴[6-7]认为影响长江中下游河道崩岸的自然因素可分为水流泥沙运动条件和河道边界条件2大类，并指出崩岸的实质首先是水流携沙与泥沙输移的动态结果，其次是河道边界条件抑制或促进崩岸的发生。宗全利等[8]、夏军强等[9]、刘昭希等[10]、王军等[11]通过现场采样，研究了荆江河岸土体力学特性，认为河岸土体组成是影响崩岸的重要因素，且河道水位变化是导致河岸稳定性周期性变化的重要原因。概化模型试验方面，岳红艳等[12]采用塑料模型沙填筑二元结构河岸，通过室内概化模型试验研究，提出了二元结构河岸崩塌的5个阶段，并总结了河岸坡比、上下土层厚度和流量等对崩岸的影响。宗全利等[13]通过试验研究了荆江河段二元结构河岸崩塌机理，认为上荆江崩岸以平面滑动为主，下荆江崩岸以绕轴崩塌为主，并根据二元结构河岸在不同时期(枯水期、高水期和退水期)的崩塌形式及过程，提出了相应的崩塌计算模式。数值模拟多从土力学角度出发，依据各类崩塌模式和临界指标进行稳定性分析，主要以Osman和Thorne[14]提出的均质黏土河岸稳定性分析模型为代表，该模型考虑了冲刷作用下的河岸横向展宽、临界坡度、岸坡所受剪切力等因素的影响。此外，部分学者以数值模型为基础进行了河岸稳定性分析，如马崇武等[15]通过计算黏性土河岸稳定性，发现水位涨落对河岸稳定性有重要影响；王博等[16]借助BSTEM模型中的岸坡稳定性模块，计算了不同水位条件、岸坡形态和岸顶植被对稳定性的影响；邓珊珊等[17]考虑了水位变化过程中河岸潜水位的变化，在此基础上通过河岸稳定性分析，研究了上荆江河岸稳定系数随水位变化的过程。

上述研究表明，崩岸的发生不仅受水流冲刷作用、河岸土体组成等因素的影响，还与河道水位变化密切相关。通过数值计算可以直观地模拟水位变化条件下河岸内孔隙水压力分布情况，并得到河岸稳定系数，但较少关注河岸实际的变形情况、崩塌过程以及崩塌模式。概化模型试验大多采用原型沙且尺度较小，也较少结合河岸土体内部应力(如孔隙水压力)监测进行研究。本文在以往研究的基础上，采用塑料模型沙进行概化模型试验，观察河岸崩塌破坏发展过程、监测孔隙水压力变化情况，初步分析水位变化速率对崩岸的影响，并结合数值计算模拟不同水位变化速率条件下岸坡稳定性的演化特征。

2 概化模型试验

2.1 试验方案

试验在封闭水槽内进行，水槽尺寸为5 m×3 m×1 m(长×宽×高)。岸坡土体横断面上下土层厚度比为1∶2的梯形设计，高度为54 cm，另外河床床沙厚30 cm，河岸坡比为1∶1，河岸横断面布置见图1。河岸土体采用分层填筑，每层铺填厚度为20 cm，以确保河岸土体的均匀性。本次试验在河岸内埋设了4个孔隙水压力传感器，用于监测水位变化情况下孔隙水压力的变化过程。岸坡制模时将传感器按相应位置埋入，并且在土体填筑过程中要做好仪器防护以防损坏。

图1 横断面布置

为模拟天然河道二元结构河岸，以长江中游下荆江河段土体作为原型参考。本次模型试验主要作用力为重力、渗透力等，且重力起主导作用，因此需满足重力相似准则。模型沙的选取首先需要满足运动相似条件，试验中取原型与模型的水深比尺λh=40，则流速比尺λu=λh1/2=6.32(模型沙与原型沙满足起动相似与扬动相似)。根据试验相似设计，试验中选用2种不同粒径的新型复合塑料沙，上层为中值粒径0.058 mm的细沙，下层及河床为中值粒径0.2 mm的粗沙，分别模拟二元结构河岸上层黏土和下层非黏性土。

试验工况包括水位快速降落和缓慢降落2种情况，以对比分析水位降落速率对河道崩岸的影响。模型边坡制备完成后，向河道内缓慢注水至水深45 cm，待边坡达到饱和稳定后，开启尾门排水，降水速率分别为0.1 m/h和0.3 m/h。

2.2 试验成果分析

2.2.1 崩塌过程及模式

图2为不同水位降落速率条件下的近岸河床地形变化。由图2可知水位变化速率对河岸崩塌有重要影响。通过试验观测，在水位涨落过程中，河岸崩塌主要经历了3个阶段,如图3所示。

图2 不同水位降落速率下近岸河床地形变化

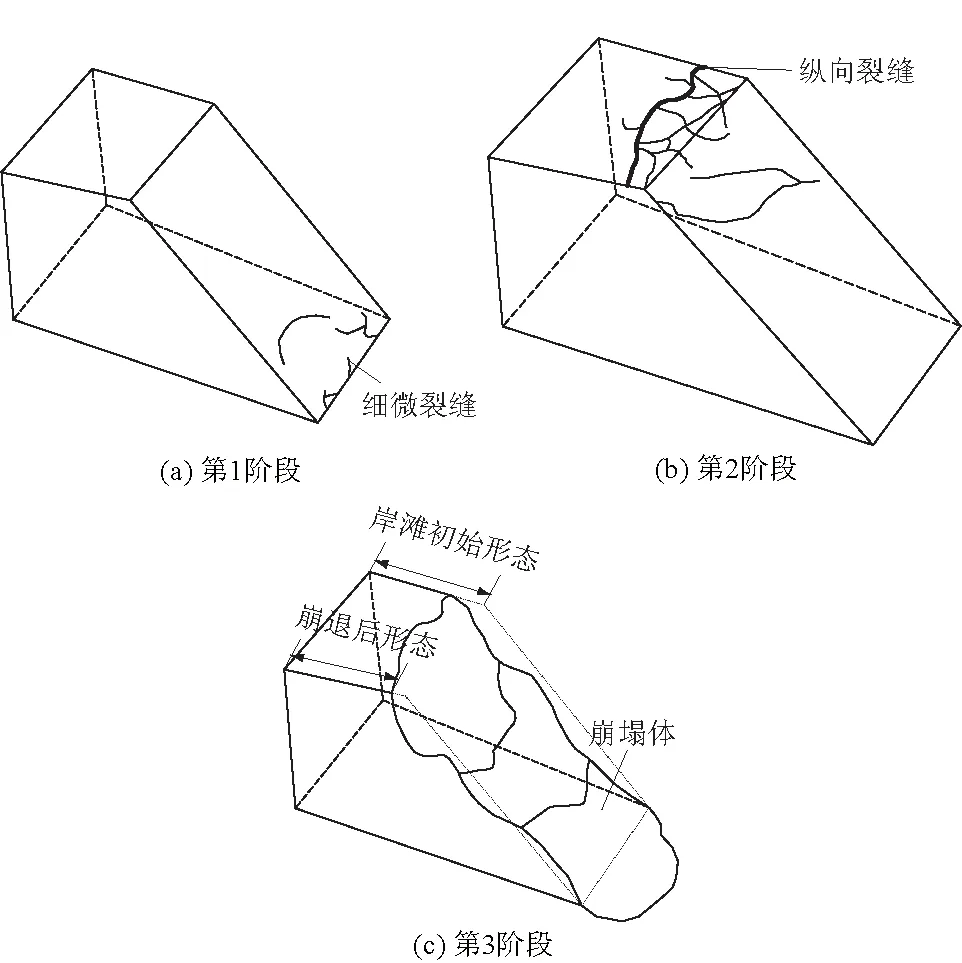
图3 河岸崩塌过程示意图

第1阶段，在水位缓慢上涨过程中，岸坡比较稳定，局部坡面产生细微裂缝，崩岸现象较少发生，近岸地形变化不大，如图3(a)所示。第2阶段，随着河道水位上涨并稳定在高水位，河岸土体受浸泡软化，岸顶出现纵向裂缝，并不断发育展宽变长，最宽处约1 cm，并且裂缝向四周发育逐步扩展至坡面，河岸形态开始发生变化，河岸表面部分土体沿岸坡滑落，如图3(b)所示。第3阶段，由于水位降落速率不同，观察到河岸崩塌破坏强度也有所差异：在水位快速降落过程中，河道内水位随之急剧回落，河岸稳定性大幅降低，河岸土体在自身重力及渗流作用下沿纵向裂缝发生崩塌，最大后退距离达20 cm，如图3(c)所示；相比之下，在水位缓慢降落过程中，崩岸较少发生，局部岸滩上的裂缝有所展宽但并未发生崩塌，岸坡形态与高水位时期的地形相比变化不大。

2.2.2 孔隙水压力变化特征

图4给出了水位陡降工况下河岸内各点实测孔隙水压力和实际水深变化情况。在河道水深上升至0.45 m的过程中，孔隙水压力也在不断增加，靠近河岸坡面处的测点最先出现读数，且读数增大的幅度要明显大于岸坡内测点读数增加的幅度。当水位稳定至0.45 m后，仍可见孔隙水压力逐步增大，水体还在向河岸内入渗，岸坡内非饱和区域越来越小，当土体饱和后各测点孔隙水压力基本一致，约为6.7 kPa。在水位降落阶段，各点孔隙水压力整体开始下降，P-1点距河道较近，孔隙水压力消散较快，其变化值基本与河道水位变化一致且变化幅度最大，而随着河岸内孔隙水压力测点距河道的距离增大，孔隙水压力变化幅度受河道水位变化的影响在逐步减小，孔隙水压力变化幅度明显小于河道水位变化幅度。如当河道水位下降15 cm，水深为30 cm时，离河岸较远的P-3、P-4点测得的孔隙水压力分别为6.25、6.51 kPa，其相应于高水位孔隙水压力的变化值分别为0.35、0.19 kPa，远小于水位下降15 cm所对应的1.5 kPa，且随着河道水位的进一步降落，各测点孔隙水压力的差值也将继续增大，差值越大，渗透坡降也越大，不利于河岸稳定。而当水位缓慢降落时，各点孔隙水压力的差值要小很多，渗透坡降较为平缓。

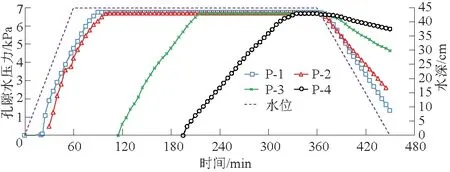
图4 孔隙水压力随时间变化过程

3 河岸稳定性计算模型

在进行水位变化情况下的岸坡稳定性分析时，需要考虑在水位变化过程中渗流对崩岸的影响。对于水位升降引起的非稳定渗流，国内外学者多采用假定边界条件随时间变化的渗流自由面的方式确定浸润线，进而通过极限平衡法计算岸坡稳定系数。本文拟采用理正岩土软件进行岸坡稳定性分析，先进行水位随时间变化的渗流分析计算，从而得到不同时段岸坡内浸润线、孔隙水压力分布情况，再进行岸坡稳定性分析。

表1 土体力学性质参数

3.1 渗流分析计算

基于非饱和土理论和基本渗流理论，二维非稳定渗流微分控制方程为

(1)

式中：H为总水头；Kx和Ky分别为水平和竖直方向的渗透系数；Q为施加的边界流量，当不考虑降雨入渗时可取为0；Ss为单位储水系数(当潜水面上升时为饱和差，下降时为给水度)；t为时间。

对于二维渗流分析计算模型，通常采用有限元法求解，渗流有限元方程形式为

(2)

式中：[K]为渗透系数矩阵；{H}为总水头向量；[M]为单位储水矩阵；{Q}为流量向量。

在计算过程中，初始压力水头取初始水位形成的稳定渗流的结果，认为流量边界q(x,y,t)恒为0。

3.2 岸坡稳定性计算

岸坡稳定分析采用极限平衡法中的瑞典圆弧法。假设河岸崩塌形式为圆弧滑动，采用瑞典圆弧滑动法，将河岸土体划分为1 m宽的土条，且滑动面上各点同时达到极限平衡状态。岸坡稳定系数F可以由滑动面上抗滑力FR与滑动力FS之比表示，即F=FR/FS，当F低于某一临界值即可认为河岸发生崩塌。

抗滑力FR主要由土体黏聚力及重力、浮力和渗透力等在滑动面法向上的合力的函数构成，即

FR=∑{c′bsecθ+[(W1+W2)cosθ-

(u-Zγw)bsecθ]tanφ′} 。

(3)

其中u=γwZ′。滑动力FS主要由重力及渗透力在滑动方向分量的合力组成，即

FS=∑(W1+W2)sinθ。

(4)

式中：b为土条的宽度(m)；W1为水位以上土条的重力(kN)，浸润线以上取重度，以下取饱和重度；W2为水位以下土条重力(kN)；Z为水位高出土条底面中心点的距离(m)；Z′为浸润线到土条底面中点的距离(m)；u为孔隙水压力(kPa)；θ为重力方向与通过土条中心点半径的夹角；γw为水的重度(kN/m3)；c′和φ′为土体抗剪强度指标。

3.3 计算参数选取

选取的计算参数包括岸坡形态、土层结构、土体力学特性及水位变化情况。北门口河段位于下荆江，河岸为上层粉质黏土与下层细砂组成的典型二元结构河岸，并且河岸下部砂土层较厚，下部砂土层又可分为松散-稍密粉细砂和中密粉细砂。如图5，根据北门口河段岸坡土体情况，岸坡形态可概化为如下：河底高程15 m，坡比为1∶2.5，并根据土体性质不同分为上下2层，上部黏性土厚度约4.2 m，下部细砂层厚33.8 m，另外假设同类土体都为均匀分布。

图5 北门口河段岸坡概化形态

河岸土体力学特性参数，包括土体黏聚力c、内摩擦角φ、重度γ、渗透系数k等通过查阅相关资料得到(详见表1)。

为研究水位变化速率对崩岸的影响，根据北门口上游石首站实测资料获得的2017年5—9月份逐日水位过程(见图6)，模拟从水位上涨阶段至水位降落阶段，设计概化水位变化工况如下。水位上升阶段：水位从31 m上升至36 m，水位上升速率0.2 m/d，持续时间25 d；高水位阶段：水位维持在36 m，持续时间20 d；水位降落阶段：水位从36 m降至32 m，水位下降速率0.2 m/d，持续时间20 d。

图6 2017年石首站水位变化情况

4 岸坡稳定性分析

4.1 岸坡稳定系数随水位变化过程

根据上述岸坡概化形态和水位变化过程，借助数值模拟开展渗流和岸坡稳定性计算分析，得到岸坡稳定安全系数的变化规律(见图7)。下面按照涨水阶段、高水位阶段、落水阶段分别进行分析。

图7 稳定系数和水位随时间的变化曲线

4.1.1 水位上涨阶段

在水位上涨过程中，河道岸坡的稳定系数随着水位升高而变大。当水位上涨时，侧向水压力增加，河道向岸坡内的渗流可以抵消一部分坡体的滑动力；其次在开始阶段孔隙水压力变化不大，河岸内的基质吸力还较大；同时水位上升导致岸坡含水率变大、抗剪强度减小的幅度较小，从而岸坡的稳定系数随着水位上涨而变大，河岸较稳定，此阶段崩岸发生概率不大。

4.1.2 高水位阶段

此过程河道内水位达到较高值，侧向水压力对河岸土体的支撑作用达到最大；随之孔隙水压力达到稳定，基质吸力变小，以及土体含水率较高(或达到饱和)，土体抗剪强度小，岸坡稳定系数出现变小的情况，将促进崩岸发生，随着时间的持续，岸坡内浸润线与坡外水位一致时，稳定系数开始保持稳定。总体来说，在高水位阶段岸坡稳定系数为先减小后不变。

4.1.3 水位降落阶段

在退水期，岸坡稳定系数进一步减小，且趋于平缓。在这个过程中，水位降落导致岸坡侧向水压力逐渐消失；岸坡内的水流渗透方向由岸坡指向河道，渗透坡降随着水位降落而增大，且岸坡下层细砂可能发生潜蚀，将使岸坡土体的滑动力增加；岸坡土体被高水位浸泡后，坡体软化抗剪强度降低，这些因素都不利于岸坡稳定，从而使岸坡稳定系数变小，崩岸发生机率增大。

需要指出的是，在此计算中并未考虑水流冲刷作用对崩岸的影响。以往研究表明，水流冲刷作用是河道崩岸的最主要因素，故若考虑水流条件，岸坡稳定系数将进一步降低。可见，在冲刷作用剧烈的洪水期和冲刷稍弱的落水期都很容易引发崩岸。

4.2 水位不同降落速率对崩岸的影响

在水位降落过程中，不同水位降落速率V对崩岸的影响不同，图8给出了水位降落速率在上述基础上(V=0.2 m/d)及增大1倍和减小1倍后，对岸坡稳定系数的影响。由图8可知，水位降落速率越小，河岸稳定系数随水位降落减小的幅度越小。这是由于水位下降得越慢，岸坡向河道方向的渗透坡降越小，坡体的滑动力也相对偏小。但随着时间的增长，岸坡内的水不断被排出，指向河道方向的力逐渐减弱，稳定系数反而有所增大。

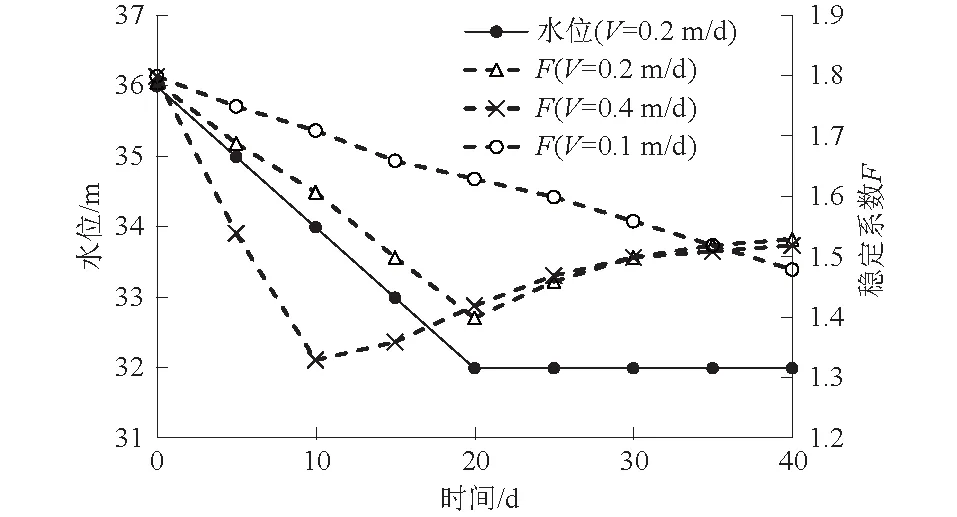
图8 不同水位降落速率下的稳定系数

以上研究表明，河道水位降落速率加快将不利于岸坡的稳定，导致河道崩岸机率增加。

5 结 论

本文通过概化模型试验初步分析了不同水位变化速率对河道崩岸的影响，并结合数值分析计算水位变化对岸坡稳定性的影响，得出如下结论:

(1)通过概化模型试验研究总结出了二元结构河岸在水位变化情况下的一般崩塌模式；孔隙水压力监测表明，岸坡内孔隙水压力消散的滞后作用是导致河岸失稳的重要原因，且水位降落速率越快，这种滞后现象越明显。

(2)河岸稳定系数基本随水位涨落而变化，随着水位上升而增大，随着水位降落而减小，在水位降落阶段，水位下降速率越大，稳定系数越小，这与试验中观测到的河岸崩塌情况比较一致。

(3)由于受试验条件和时间的限制，试验考虑的因素还较少，今后也还有很多工作要做，如冲刷条件下的试验研究还未能完全开展，模型沙与原型沙力学性质的相似模拟还需进一步完善等。