基于SDPD的动态浸润研究

土俊鹏，刘汉涛,李海桥

(中北大学能源动力工程学院，山西 太原 030051)

随着对自然界浸润现象的深入研究，各种结构表面的浸润性能受到了广泛关注，目前不同浸润性表面仿生材料的开发与应用成为科学研究的热点和难点之一[1-3]。在表面材料浸润性能的研究过程中发现，材料自身属性起着非常重要的作用，多相间表面张力的协同作用是决定表面材料性能的最重要因素之一[4-6]。多相间表面张力的相互作用是一个复杂的动态过程，这个过程涉及到流体结构大变形，且本质上是一个跨尺度的复杂物理现象。对动态浸润问题进行实验研究是非常困难的，很难复现动态浸润过程中的真实物理条件和流体动力学行为。数值模拟技术的发展给深入研究动态浸润问题提供了便利，但基于网格的流体模拟方法很难捕捉多相间复杂的界面力学行为，在处理动态浸润过程中涉及的流体结构大变形还会遇到网格畸变等固有问题的困扰。无网格方法在处理上述问题时具有独特的优势，其中光滑粒子动力学(smoothed particle hydrodynamics, SPH)作为最早的无网格方法之一，在研究多相流动等复杂流体动力学行为时受到了广泛关注[7-8]。然而，SPH是一种宏观尺度的计算方法，不能准确刻画复杂流体动力学行为中的多尺度机理[9]，因此Espaol等[10-11]将SPH和与耗散粒子动力学(dissipative particle dynamics, DPD)无网格方法相结合，提出了光滑耗散粒子动力学(smoothed dissipative particle dynamics, SDPD)方法。与DPD方法一样，SDPD中考虑了粒子的热运动，引入了随机运动，可以描述介观系统的随机振荡，因此SDPD能够从介观尺度上揭示浸润问题内部复杂的流体动力学行为。但欲真正揭示浸润问题的内部机理，准确描述气体、液体以及固体间复杂的界面张力是需要解决的最关键的问题之一[12]。鉴于SDPD方法自身的优势和特点，近年来已经应用到研究复杂多相流问题中[13-14]，其中Hu等[15]构建的多相流模型受到了广泛关注，虽然该模型在研究固体表面上的浸润问题已有较多的应用，但很少有该模型在通用性方面的研究。本文基于Hu等提出的SDPD模型，不仅研究了普通的亲疏水问题，还研究了超亲疏水问题，通过系统地对比研究，结合研究成果和动态浸润过程中流体动力学行为，对利用SDPD模型研究浸润问题的通用性进行讨论，同时对该模型存在的问题进行剖析，并给出改进意见。本文的工作为揭示浸润问题的本质提供了理论依据，同时为SDPD方法的发展和改进打下了理论基础。

1 数值研究方法

1.1 SDPD方法

SDPD方法演化方程的通用表达式可以写成：

dri=vidt

(1)

(2)

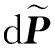
(3)

式中：ρ，m分别为粒子的密度与质量；σ为粒子的数量密度；W为核函数；下标i和j为粒子的编号。

保守力FC的表达式为：

(4)

(5)

式中：η为动力黏度;上标k和l表示不同的相；vij为从粒子i到粒子j的速度矢量。

根据GENERIC形式[16]中动量耗散形式，随机力的表达式可以写为：

(6)

其中

(7)

式中：kB和T分别为玻尔兹曼常数和系统温度。本文采用五次样条核函数[17]，其表达式为：

(8)

式中：W(R,h)为光滑核函数，其中R为两粒子间的相对距离，h为光滑核函数W影响区域的光滑长度；αd为处理不同维数问题时的正则化参数，本文计算的是二维问题，αd=7/478πh2。粒子由于密度变化引起的压力变化采用人工状态方程[18]求解，其表达式为：

(9)

式中：p(ρ)为粒子压力；p0,ρ0为参考值；γ通常为7。

1.2 表面张力模型

本文用连续表面张力模型[19]计算相与相之间的界面张力Π(1)，其表达式为：

(10)

(11)

在相内部，色函数的梯度是为0的，而在相与相的界面处，支持域内粒子分别属于不同相时，色函数的梯度不为0，色函数梯度的计算式为：

(12)

(13)

式中：d为计算域的维度。粒子i总的表面张力为：

(14)

最终可以得到角动量和线动量均守恒的表面张力表达式：

(15)

固壁边界处理是实现浸润问题准确计算的关键之一，本文采用文献[15]中的方法，即利用镜像粒子边界[19]实现无滑移边界条件，使用CFL[20](courant-friedrichs-levy)条件对时间步长进行估算。

2 结果及分析

2.1 计算模型及液滴变化过程

在不考虑重力的前提下，根据杨氏方程，固体表面上三相间的接触角θ满足α1w=α12cosθ+α2w，其中上标1,2和w分别表示气体、液体和固体，即α1w，α2w,α12分别为气体与固体、液体与固体、气体与液体间的表面张力。调节三相间的表面张力系数，并运用θ=2arctan(2H/L)来测量液滴的接触角，如图1所示。本文选择超亲水(理论接触角接近10°)和超疏水(理论接触角为170°)进行研究，深入研究该方法对超亲、疏水的适应性。

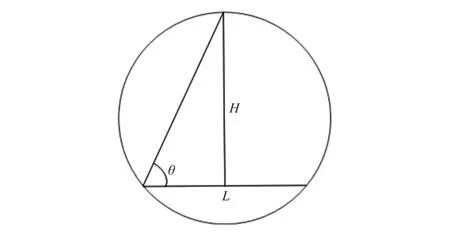
图1 接触角计算模型图

本文计算模型的物理尺度为介观尺度。在计算亲、疏水时，若粒子间距离相同，则采用相同的光滑长度。在计算超亲水时，由于液滴铺展长度较大，因此计算区域选定为0 μm

图2 初始粒子分布

计算超亲水动态浸润时的液滴形态以及流场的变化状况如图3所示。液滴顶部有向内汇聚的流动，而在固体表面上，液体沿着壁面动态铺展，尤其在三相接触点的位置，液体的运动更加明显，由于液滴顶部和底部运动方向相反，在液滴的腰部产生了明显的涡，使得液滴形貌在很短的时间内发生了剧烈变化。随着时间的推移，液滴周围的区域还有明显的运动，而在内部靠近壁面的液体在无滑移边界条件的作用下，速度越来越小。当液滴外部的曲率趋于一致时，表面张力趋于平衡，液滴在黏性力作用下，慢慢趋于稳定。液滴稳定后，根据θ=2arctan(2H/L)计算可得接触角为27.3°，与理论值有较大的偏差。

图3 超亲水模拟变化过程

计算超疏水时，由于没有长距离的铺展，计算区域选定为0 μm

图4 超疏水模拟变化过程

2.2 结果分析

通过上述研究，发现Hu等提出的方法在计算超亲水或超疏水现象时有很大的误差，为了更系统地研究该模型产生误差的原因，设定α1w=1，α12=1，通过改变α2w的值来计算接触角。从图5可以看出，在亲水性模拟中计算得到的液滴接触角比理论角度都大，在疏水性模拟计算中比理论角度小，在90°附近误差最小，为1%，60°～120°时的误差在5%以内，基本满足计算精度的要求，但在计算超亲水和超疏水角度时误差比较大。由于液滴铺展长度的变化比液滴高度的变化明显，为进一步探讨该模型的计算精度，通过改变不同条件，研究液滴铺展长度的变化规律。其中液滴铺展理论长度的计算方法采用Thmas[21]提出的方法，该方法中铺展长度L与接触角的关系为L=2Rsinθ，其中曲率半径R是液滴的截面积A和接触角θ的函数：

(16)

图5 计算角度与理论角度对比图

计算区域不变，当粒子间距为0.083 μm和0.042 μm时，对应液滴内粒子数目分别为216和648，两种分辨率下的计算结果如图6所示。当粒子间距减小，粒子数目增加时，在计算亲水角度时，液滴铺展距离更长，在计算疏水角度时，液滴收缩程度更高，说明随着粒子数目的增加，计算精度会提高。

图6 不同分辨率计算结果

选定与理论角度出现较大偏差的超亲水(10°)，计算液滴内粒子数目从216到1 080时液滴长度与理论值的相对误差，结果如图7所示，由图可知，随着液滴内粒子数目的增加，其接触角与理论值的偏差逐渐减小，说明在接触角附近，通过提高分辨率可以更细致地刻画液滴的铺展过程。

图7 相对误差曲线

SDPD方法中，用随机力来模拟粒子热波动，由式(7)可以看出，计算尺寸对随机力的计算有显著影响。设系统温度为300 K，计算模型不变，粒子数目一定(液滴内粒子数为216)，通过改变粒子单元的尺寸来改变计算区域的大小，粒子单元尺寸分别为0.10 μm×0.10 μm，0.25 μm×0.25 μm和1.00 μm×1.00 μm。在这3个计算尺寸下计算多个接触角对应的液滴铺展长度，并对应到同一坐标系中。从图8的对比结果可以看出，不同尺度的液滴总体变化规律相近，但对应的铺展长度会因为粒子热波动呈现轻微的差异。

图8 不同计算尺寸的影响

图9所示是3个不同尺寸液滴达到稳定状态时的粒子分布(60°)，由图可知，粒子单元尺寸越小，液滴外轮廓越不规则，内部粒子分布无序度越高；粒子单元尺寸越大，外轮廓越光滑，内部粒子分布越具有一定的规律性。由此可证明，由随机力引起的热波动随着粒子单元尺寸的减小而显著增大，表明了SDPD方法能描述介观尺度不同物理尺寸的热波动特性。

图9 不同单元尺寸液滴平衡状态时粒子分布图

就目前的研究结果可以看出，镜像边界处理方法中壁面粒子的位置会随着流体粒子位置的改变而发生改变，当边界处压力梯度较大时，产生较大的排斥力，会导致边界粒子与流体粒子的距离增大，致使局部区域粒子变得稀疏，影响计算结果，采用固定的边界粒子，可以消除由此引起的误差。在计算超亲水和超疏水时，通过两种接触角的求解方法，均没有达到预期的结果，这表明：1)通过稳定时液滴外轮廓的曲线方程，求出三相点处的曲线斜率的方式求出接触角，可以更准确地计算出接触角的大小；2)除了表面张力的作用外，还有固体微结构与液体间的相互作用，可以通过引入特殊的液固粒子间作用力模型来处理相关的问题，减小超亲水和超疏水接触角计算误差；3)本文在计算过程中，并未考虑能量方程，而在超亲水或超疏水现象中，能量的变化也有一定的影响，考虑能量方程可以更加准确地刻画超亲水或超疏水现象。通过减小粒子间的距离可以在一定程度上提高计算精度，证明在研究超亲水或超疏水问题时，通过提高分辨率可以刻画浸润过程中的更多细节，引入粒子自适应划分技术，细化三相接触线及其附近的区域，可以更好地研究各类浸润问题。

3 结论

本文基于SDPD方法研究超亲水和超疏水两种特殊的浸润问题，结果表明：

1)SDPD方法在计算超亲水或超疏水等涉及流体结构大变形问题时，方法自身的粒子自适应分布能够捕捉多相间复杂的界面力学行为，为研究各类复杂的介观尺度浸润问题提供了可靠的数值方法；

2)Hu等提出的多相流模型和镜像边界条件在处理浸润问题时，当接触角为30°～135°时基本能满足计算精度的要求，但在研究超亲水和超疏水现象时，计算误差较大，需要引入其他方法来缓解计算中误差较大的问题。