3-RSR并联机构工作空间的研究
罗建国,王 婷,王宇强
(1.华北科技学院机电工程学院,河北 三河 065201)(2.河北省矿山设备安全监测重点实验室,河北 三河 065201)(3.华北科技学院安全工程学院,河北 三河 065201)
并联机构具有刚度较大、结构稳定、误差小、精度高、易于实现高速运动、结构简单等优点,这也是并联机构比串联机构应用更广泛的原因[1]。3-RSR并联机构是一类具有1T2R少自由度的空间对称并联机构,其被广泛应用于医学、喷漆、汽车装配、精密加工、精密测量等工程领域。诸多学者对此类一移两转并联机构进行过研究[2-4],并提出了具有1T2R的不同类型并联机构。文献[5]基于拉格朗日方程建立该机构的动力学模型,并对该机构载荷以及力矩进行了分析;文献[6]对各支链转动副平行的3-RSR并联机构进行了位置求解;文献[7]~[9]对并联机构自由度、特殊位形、位置进行了分析;文献[10]~[11]基于3-RSR并联机构几何运动特性和雅可比矩阵对机构进行了奇异分析。
上述文献基于拉格朗日方程和雅可比矩阵的求解过程比较繁琐,计算量比较大,鉴于此,本文基于螺旋理论对某一类各支链3运动副轴线平行的3-RSR并联机构进行了自由度分析、正逆解求解、奇异位形分析和位置分析,并借助AutoCAD软件绘制出3-RSR并联机构的工作空间。
1 坐标系的建立及机构描述
图1所示为3-RSR并联机构运动简图。该机构由动平台B、定平台A及3个相同的支链RSR组成,每个支链的分支两端是两个转动副(R),中间是一个球铰副(S),并且球铰副上下两杆长度相等,即3个分支支链在上、下平面上对称分布,且该机构移动方向始终是与其中间平面S相垂直,即沿着Z轴在竖直方向上移动。

图1 3-RSR并联机构
定平台和动平台坐标系分别是O-XYZ、p-xyz。设θi为AiSi绕转动副Ai的轴线逆时针旋转至与O-XY平面平行的转角;φi为SiBi绕球铰副Si的轴线逆时针旋转至与O-XY平面平行的转角;OA2和OA3与OA1的夹角分别为δ2,δ3;转动副Ai和球铰副Si轴线之间的距离为ai,其中a1=a2=a3=a;球铰副Si和转动副Bi轴线之间的距离为bi,其中b1=b2=b3=b;动平台和静平台内接圆半径分别为r,R。
2 自由度分析
本文基于螺旋理论(反螺旋)的自由度分析原理和修正Kutzbach-Grübler公式,求解机构的自由度分析空间3-RSR并联机构的自由度[12]。图2为3-RSR并联机构在任一位形下的单支链结构图,动平台与静平台始终保持平行。在支链i的Si上建立坐标系Si-xiyizi,其中xi轴与转动副Ai的轴线平行,yi轴与转动副Ai的轴线垂直,zi轴的方向按照右手螺旋定则确定,即方向为垂直Si-xy平面竖直向上,则支链i运动螺旋系的5个螺旋为:
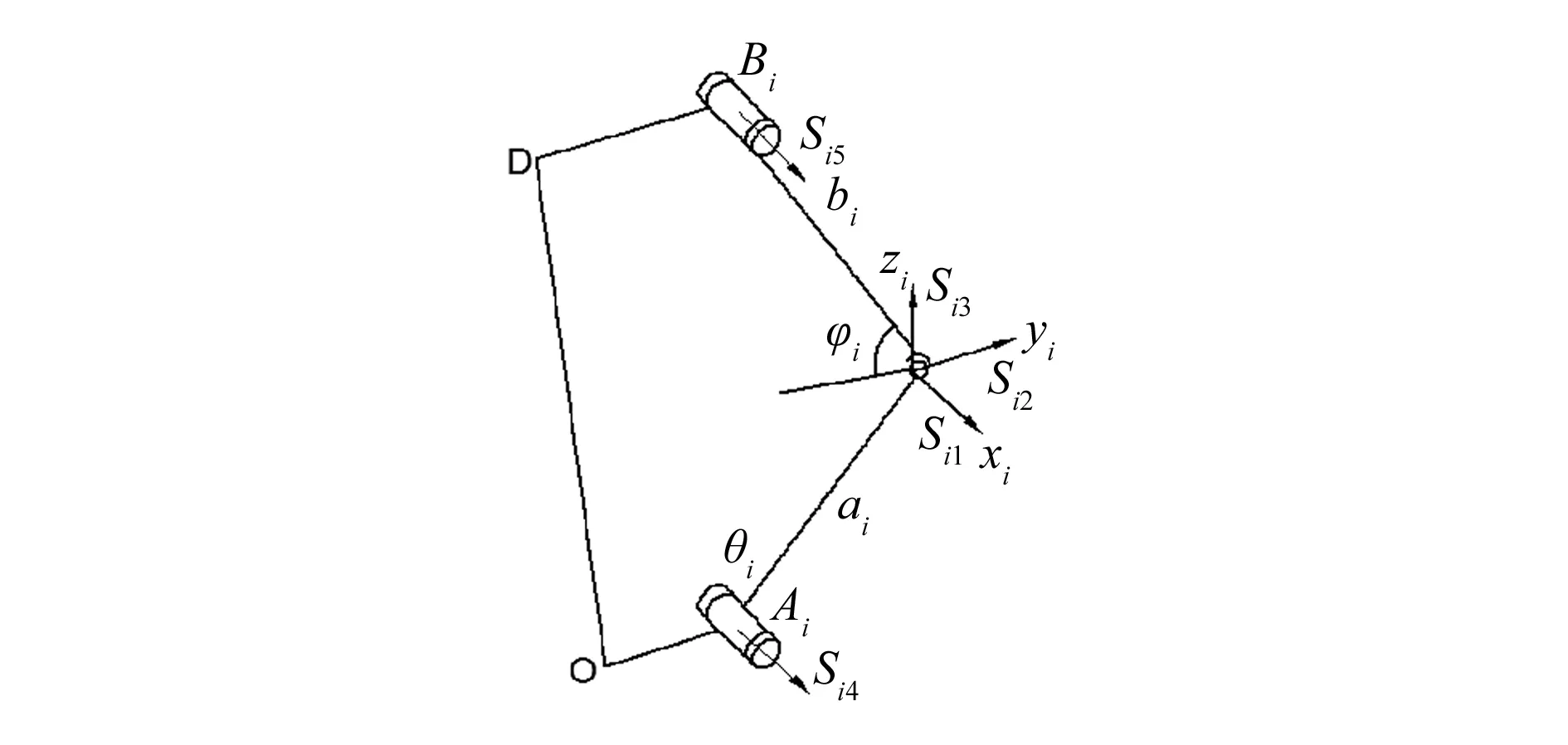
图2 单支链结构图
(1)

当支链i的3个运动副轴线不共面时,Si1,Si2,Si3,Si4,Si5线性无关,为支链i的运动螺旋系的基,即秩为5,则其约束反螺旋系的基有1个螺旋。根据螺旋的互逆性,可知反螺旋的方向,即支链i对动平台有1个约束,方向为平行于动平台且沿着x轴。在坐标系Si-xiyizi中可表示为:
(2)

综上可知,当3个支链的3个运动副轴线都不共面时,各个支链都对动平台施加了沿着X轴的力约束,即公共约束λ=1,其约束中间两个平面的移动和绕中间平面法矢的转动,从而断定整个机构的自由度为5,整个机构包含动平台和定平台,由此可以推出3条支链组成的机构的自由度为3,具有1平移2转动的运动。该机构的自由度可由修正的Kutzbach-Grübler公式计算,考虑公共约束λ=1和冗余约束ν=0,有:
(3)
式中:M为机构的自由度;d为机构的“阶”,由公共约束λ确定,d=6-λ;n为机架的构件数目;g为运动副的数目;fi为第i个运动副的自由度;ν为并联冗余约束;ζ为机构中存在的局部自由度。
3 奇异分析
上述自由度的计算过程和分析具有瞬时性,在运动过程中,经常会出现处于死点或者失去稳定等一些特殊现象,这些现象都会引起自由度的变化,进而造成一定的损坏,因此人们把机构在上述现象中出现的特殊位形称为机构的奇异位形。机构奇异位形按照形成原因可分为运动奇异和约束奇异。因此,对该机构的奇异位形进行深入研究,不仅可以减少其对机构造成的损毁,从而避免经济损失和潜在危害等的发生,还有助于提高机构自身性能,促使并联机构在工程实际应用中快速发展。
本文通过运动螺旋的线性相关性来判断机构奇异类型,当该机构的各个支链运动螺旋线性相关时,动平台的约束相应增加,引起自由度发生变化,故机构发生奇异。当机构处于上述初始位形,可知螺旋不可能发生线性相关,因此机构处于此种状态时,不需要分析奇异类型。对于本文的3-RSR并联机构,当且仅当该机构3个运动副轴线共面时,有支链的运动螺旋线性相关,使得自由度发生变化,机构处于运动奇异。本文在分析约束奇异时,选取转动副A1,A2,A3作为主动件。锁住该3-RSR所有的主动件,则获得一类各支链运动副轴线平行的3-RS并联机构,通过机构约束分布的图解,可以看出机构不同的约束类型。
将机构分为一移动和两转动自由度的位形,图3为动平台只有一移动自由度时的示意图。假设机构在运动过程中3条支链的运动副轴线共面平行,则此时的运动螺旋发生线性相关,自由度亦发生变化,因此在此种状态下机构的约束类型是运动奇异;若此时锁住定平台上的主动副,则机构自由度为0,无约束奇异。

图3 动平台只有1移动自由度
图4为动平台只有2转动自由度时的示意图。如图4(a)所示,当3条支链的3个运动副轴线共面平行时,机构的运动螺旋发生线性相关,其自由度发生变化。在此种状态下,机构的约束类型为运动奇异,无约束奇异;如图4(b)、(c)所示,当3条支链的3个运动副轴线平行不共面或3条支链各自的运动副轴线相交时,机构的运动螺旋发生线性无关,在此种状态下机构无运动奇异;若此时锁住定平台上的主动副,动平台上的约束限制机构在中间球铰副平面的移动和转动,故无约束奇异。

图4 动平台只有2转动自由度
综上所述,通过对3-RSR并联机构的奇异类型分析,可知当机构处于1移动自由度的位形,动定平台的转动副与球铰副之间的夹角达到180°,机构自由度减少,此时只有运动奇异、无约束奇异;当机构处于2移动自由度的位形,任一支链的转动副与球铰副之间的夹角达到180°,机构自由度减少,此时机构只有运动奇异、无约束奇异。故在实际工程应用中,可合理设置机构运动参数来有效避免运动奇异的产生,进而减少对机构的损坏。
4 位置求解
4.1 位置逆解
3-RSR并联机构位置逆解可简述为:已知动平台坐标系上各个转动副的坐标,求定平台上各个主动副的输入角度θi。图5所示为动平台位姿图,设动平台上点P在固定坐标系的坐标为(XP,YP,ZP),动平台相对于静平台的姿态用欧拉角表示,分别为α,β,γ,其中γ为无穷小量。根据该机构在不同的运动位形下,都有转动副Bi轴线平行于转动副Ai的轴线,从而恒有α=0、β=0、γ=0。动平台的内接圆半径为r,定平台的内接圆半径为R,根据图1的几何关系,可得到Bi在定坐标系O-XYZ中的坐标,其表达式如下:
(4)

图5 动平台位姿图
在定平台坐标系O-XYZ中,定平台上的3个转动副A1,A2,A3的坐标如下:
(5)
根据该机构的空间位置,可知Si为以Ai为圆心、a为半径的圆和以Bi为圆心、b为半径的圆的交点,Si存在即逆解存在,其必要条件为:
(a-b)2≤(xAi-xBi)2+(yAi-yBi)2+(zAi-zBi)2≤(a+b)2
(6)
当给定的P点的坐标满足式(7)时,Si存在,且由于Si特殊的空间位置关系,根据几何关系S1B1=S2B2=S3B3=b,A1S1=A2S2=A3S3=a,可建立如下表达式:
(7)
式(8)中两个方程相减后成为二元二次方程,最多可有2组解,每组解都可确定唯一的θi,可由式(8)解得:
(8)
综上可知,对于本文中的3-RSR并联机构,当给定位姿时,每条支链最多可有2组解,3条支链最多8组解,即8种位形。
4.2 位置正解
位置正解刚好和位置逆解的思路相逆,位置正解可简述为:已知定平台坐标系上各个转动副Ai的坐标以及转动副的输入角θi,求动平台的位姿(XP,YP,ZP,0,0,0)T。当给定(θ1,θ2,θ3)T时,在定坐标系O-XYZ中,球铰副Si的坐标容易由几何关系得出,Si的坐标表示如下:
(9)
将求得的Si、Bi的坐标代入式(7)中的第二个方程式,化简得到的方程为三元二次方程,最多可有8组解。
5 工作空间实例分析
假设3-RSR结构参数如下:a=b=500 mm,r=50 mm,R=100 mm,δ2=δ3=120°。将上述参数代入式(6)中,化简以后可得式(10),此式为一个三维圆柱体的表达式。
(10)
以式(10)中的3个不等式为支撑,利用AutoCAD对3-RSR并联机构的工作空间进行直观表述。具体为:根据不等式可知各个支链方程的最小和最大范围,形成3个相同圆柱体相交汇的运动空间,如图6(a)所示;基于3个圆柱体的交汇空间,利用AutoCAD中的命令INTERSECT(交集),可得该机构的包络空间,如图6(b)所示;最后利用AutoCAD查询功能显示工作空间质量特性,包括质量、体积、质心、惯性矩、旋转半径等数据,如图6(c)所示。由图7可知,3-RSR并联机构的工作空间是完全对称结构,且在x轴方向的活动空间范围较大,原因是动平台和定平台上的转动副平行于x轴线方向。
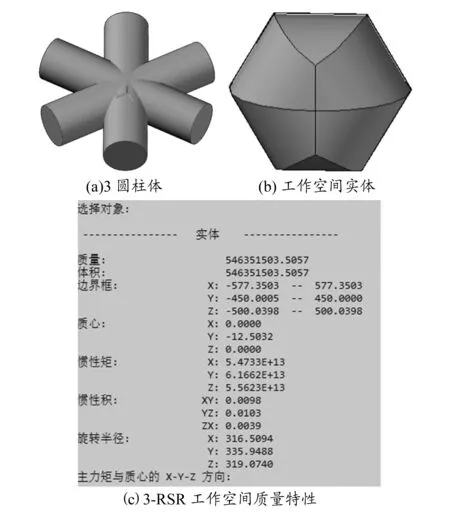
图6 工作空间求解
6 结论
1)本文基于螺旋理论(反螺旋)自由度分析原理,根据机构任一位形下3条支链的空间约束分布情况来判断自由度的变化,可以清晰地判断机构奇异类型。
2)根据数值法建立的机构位置正解和位置逆解的计算公式,可为该机构的位置求解提供快速有效的计算方法。
3)通过本文确立的3-RSR并联机构工作空间表达式,并利用三维制图软件AutoCAD中相关命令绘制工作空间,发现三维空间是3个空心圆柱的交集。

