基于接触力学的膝关节假体几何参数研究

宋春燕，刘 峰，李宏伟

(中北大学机械工程学院，山西 太原 030051)

超高分子量聚乙烯膝关节假体胫骨关节面的磨损被认为是影响膝关节假体远期使用寿命的根本因素。Abdelgaied等[1]通过仿真建模与模拟机实验，所得结果均表明膝关节假体的几何参数对假体磨损产生显著影响；王猛等[2]认为假体冠状面上的形合度是影响膝关节接触应力的关键参数，但未能定量地给出设计结果；Mazzucco等[3]指出，聚乙烯体积的磨损会随接触面积增大而增大，胫骨关节面的磨损应依据基于接触面积的磨损模型来进行评估。根据磨损与接触力学的关系[4]，当接触应力小于疲劳应力[2]时，具有较小接触面积的膝关节假体能够很大程度上减小磨损进而延长假体使用寿命。由于膝关节假体的几何参数对接触面积和接触应力的影响并不明确，因此通过改变假体几何参数来降低接触面积从而减小磨损的目的未能实现。

本文提出了基于Isight平台的膝关节假体几何参数实验设计方法，通过改变假体相关几何参数生成新的膝关节假体模型，对其进行有限元仿真，明确各几何参数对关节假体接触面积和接触应力的贡献度，得到了具有较小接触面积的优化膝关节假体模型，与初始模型进行对比，验证了实验设计方法的可靠性，为假体设计和临床选型提供了理论依据。

1 膝关节假体几何参数的选定

基于后交叉韧带保留型膝关节假体(DePuy PFC CR)[5]的几何形状，如图1所示，本文选定如下7个几何参数用于膝关节假体的参数化建模：股骨组件矢状面前端曲率半径RDF、后端曲率半径RPF、冠状面曲率半径FFR、最低点到冠状面中线的距离W、胫骨假体矢状面前端曲率半径ISD、后端曲率半径ISP、冠状面曲率半径IFR，按照表1对每个几何参数设置变量区间以生成具有实际临床意义的假体，并对几何参数之间设定不等式约束：在冠状面上IFR>FFR，在矢状面上ISP>RPF，ISD>RDF。

图1 4个几何参数控制的胫骨参数化模型

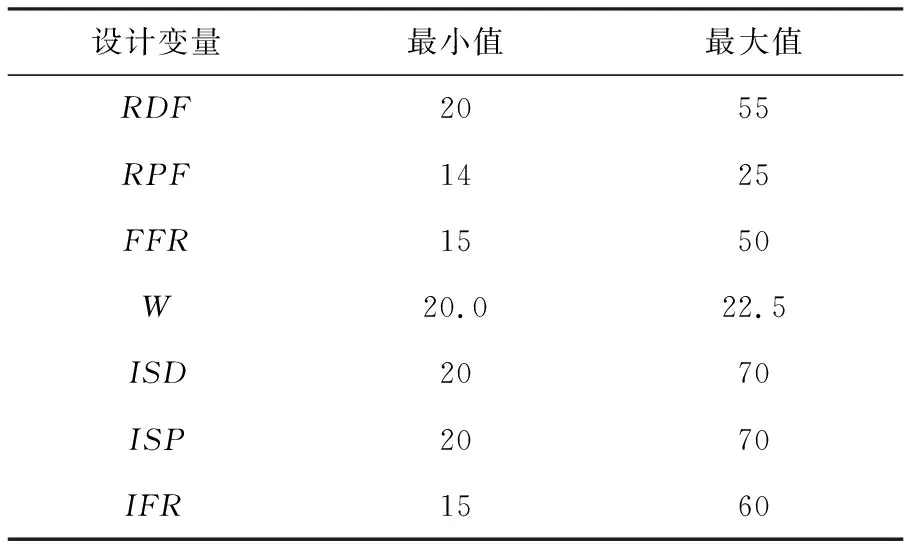
表1 生成参数化假体模型几何参数变量区间 单位：mm

2 基于Isight平台的实验设计

2.1 假体有限元参数建模

本文采用最优拉丁超立方抽样方法将表1中的每个变量在最小值与最大值之间均匀地划分为400个区间，每个区间中随机抽取一个样本，形成一个400×7的样本矩阵。使用Isight软件中的实验设计模块对样本矩阵中的所有样本点进行读取，每读取一个样本点就调用一次SolidWorks生成新的股骨与胫骨假体模型，通过Python子程序将生成的模型导入到ABAQUS中进行有限元分析，并输出模型的性能指标(最大接触面积和最大接触应力)，Isight平台读取模型的性能指标作为输出参数。

如图2所示，使用文献[3]中的有限元方法对股骨和胫骨假体的材料进行设置，划分网格时股骨采用2.5 mm的四面体网格，胫骨采用2 mm的六面体网格，两组件之间是摩擦系数为0.04的罚接触[6]。边界条件的设定基于ISO 14243-3:2014标准[7]：在股骨参考点处施加屈曲角度和轴向的垂直载荷，在胫骨参考点处施加内外侧旋转角度和前后位移，约束除股骨内外翻运动外的其余自由度。

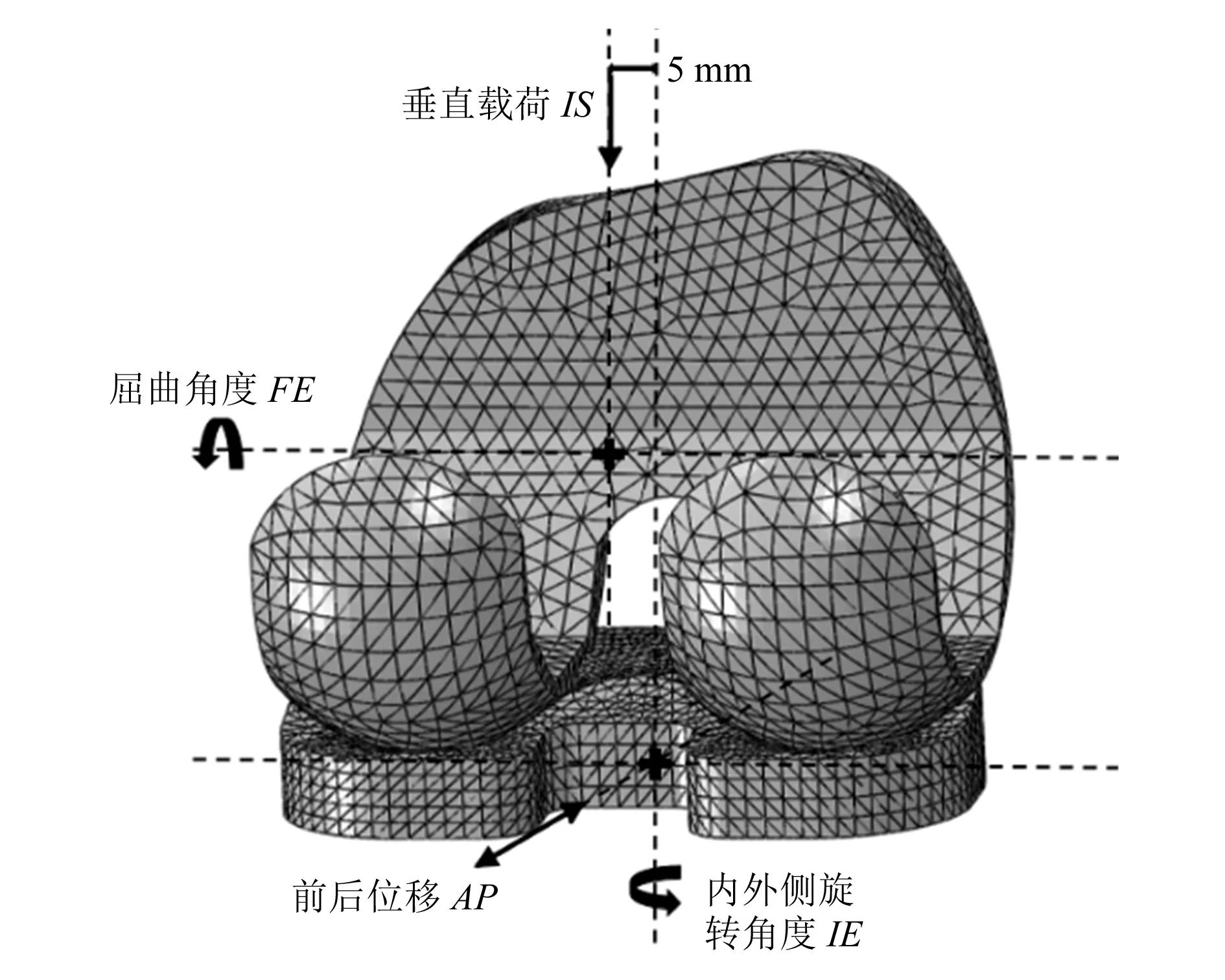
图2 假体有限元分析参考点及载荷分布

2.2 几何参数对性能指标的贡献度

为了确定几何参数对性能指标的贡献度，Isight根据样本点建立如下多元二次回归模型[8]：

(1)

式中：xi,xj为输入参数，i,j=1,…,7，为输入参数的编号，i≠j；β0,βi,∂i,δij均为变量的系数；yσ为性能指标，σ=1,2，为输出参数的编号。

对式(1)进行微分：

dyσ=∑βidxi+2∑∂ixidxi+∑δijdxixj

(2)

第i个几何参数对性能指标的线性主效应Mxi为：

Mxi=βidxi

(3)

(4)

第i，j个几何参数对性能指标的交互效应Mxixj为：

Mxixj=δijdxixj

(5)

分别使用最小二乘法将各个几何参数的主效应及交互效应归一化到[-1,+1]，得到系数Sxi，并转化为百分比形式的贡献率。贡献率Nxi计算公式为：

(6)

依据式(6)的结果得到各几何参数对于性能指标的贡献程度，在Pareto图上与式(4)、式(5)的结果进行对比显得更加直观，因此将式(6)的结果按照其绝对值在Pareto图中从大到小排列。当几何参数的二次项效应贡献占比较大时，查看主效应图，进一步确定几何参数对性能指标的影响趋势；当参数之间存在交互效应且贡献占比较大时，说明其中一个参数对性能指标的影响会随另一参数的变化而改变，在后续优化研究中应综合考虑。

3 结果与分析

3.1 各个因子对性能指标的贡献度

如图3,4所示的Pareto图中，实心线条代表步态周期响应与因子呈正相关，空心线条代表二者呈负相关。FFR、IFR是影响接触面积与接触应力的主要因子，但作用相反，FFR与接触面积呈正相关，与接触应力呈负相关；IFR与接触面积呈负相关，与接触应力呈正相关。理论上可通过降低FFR、增大IFR来减小接触面积，但FFR与IFR对接触面积与接触应力的交互效应(IFR-FFR)贡献度都较大，说明因子FFR对接触面积与接触应力的影响会随IFR值的改变而改变，应对IFR、FFR合理取值。ISP的二次项效应对接触面积和接触应力的贡献度次之，如图5(a)所示，当ISP约为57mm时，接触面积可取较小值；如图5(b)所示，当ISP约为47 mm时，接触应力可取较小值。但由于ISP2对接触应力的贡献度更为突出，因此可取ISP=46～48 mm来保证接触应力在允许范围内，然后通过改变其他因子来得到较小的接触面积。

图3 各个因子对步态周期最大接触面积贡献占比排列

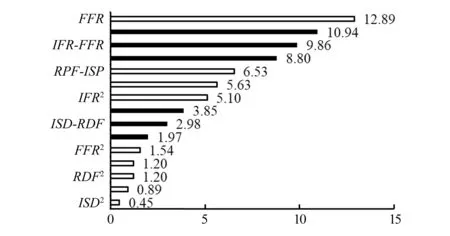
图4 各个因子对步态周期最大接触应力贡献占比排列

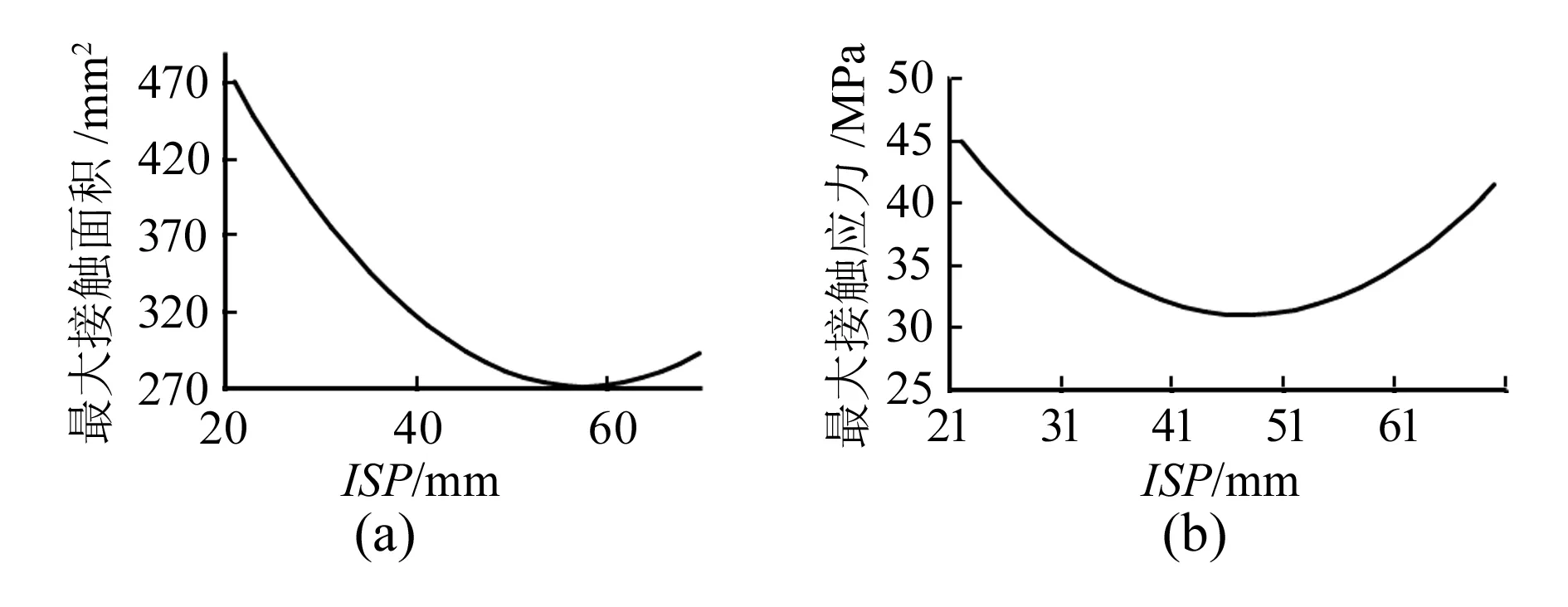
图5 ISP对步态周期最大接触面积和最大接触应力的主效应图

3.2 优化模型

3.2.1优化模型几何参数确定

表2列出了根据实验设计模块中计算的400个样本点模型而得到的一个最优模型的参数。由表2可知，相对于初始模型，优化模型的胫骨冠状面曲率半径IFR增大了72.72%，接触面积下降了32.33%，符合3.1节所述IFR增大、接触面积减小的结论；股骨冠状面曲率半径FFR增大了20.70%，这可以平衡因IFR增大而导致的较大的接触应力；ISP值47.32，符合3.1节所述其取值为46～48 mm的要求；其余参数(ISD、RDF、RPF、W)与初始模型相近。进一步证明了优化模型的合理性。

表2 初始模型与优化模型的几何参数

3.2.2接触力学对比

如图6,7所示，对比优化模型和初始模型在整个步态周期中的接触应力和接触面积变化曲线发现，两个模型均出现3个典型峰值且呈现相似的变化趋势，并分别与假体所受垂直载荷的3个峰值相对应[12]，两个模型均在13%步态周期处获得最大接触压力，在43%步态周期处取得最大接触面积。初始模型的最大接触面积为343.12 mm2，最大接触压力为29.11 MPa；优化模型的最大接触面积为232.18 mm2，最大接触压力为39.40 MPa。优化模型相较于初始模型来说，最大接触面积降低了32.33%，更有利于得到较低磨损的膝关节假体，虽然其最大接触应力增加了35.35%，但并不足以导致疲劳磨损[9]。图8,9显示了在13%和43%步态周期时刻优化模型和初始模型胫骨衬垫的接触应力和接触区域分布，由图可以看出，在冠状面上，初始模型形合度较小(IFR-FFR=1 mm)，导致胫骨衬垫的接触形状趋近于椭圆，优化模型的形合度较大(IFR-FFR=12.64 mm)，接触形状更趋近于圆形，这也使得优化模型减小了股骨部件与胫骨衬垫的边缘接触。

图6 整个步态周期初始模型和优化模型的最大接触应力曲线图

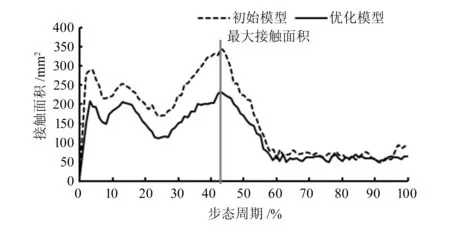
图7 整个步态周期初始模型和优化模型的最大接触面积曲线图

图8 胫骨表面在最大接触应力时的应力分布及接触面积对比图(13%步态周期)

图9 胫骨表面在最大接触面积时的应力分布及接触面积对比图(43%步态周期)

3.2.3运动性能对比

根据ISO 14243-1:2009[9]力控制数据对初始模型和优化模型进行有限元仿真，对比两个模型的运动性能，研究其在完整步态周期下胫骨衬垫的内外转角和前后位移的变化。如图10所示，优化模型胫骨衬垫前后方向的位移基本与初始模型保持一致(-3.34～0.80 mm)，这与Ardestani[10]的研究结果相同。如图11所示的内外旋转运动，相较于初始模型胫骨衬垫所达到的最大内旋角度(6.8°)[2]，优化模型的胫骨衬垫获得了更大的内旋角度(8.4°)，可进一步提高假体的运动性能。

4 结束语

本文基于Isight平台对400个膝关节假体模型进行有限元分析，根据多元二次回归模型得到了几何参数对关节假体接触面积和接触应力的贡献度排序，最终确定股骨冠状面半径FFR、胫骨冠状面半径IFR与胫骨矢状面后端半径ISP是接触面积和接触应力的重要影响因子，并获得了性能指标更优的优化模型，对后续的膝关节假体优化有一定的指导意义。

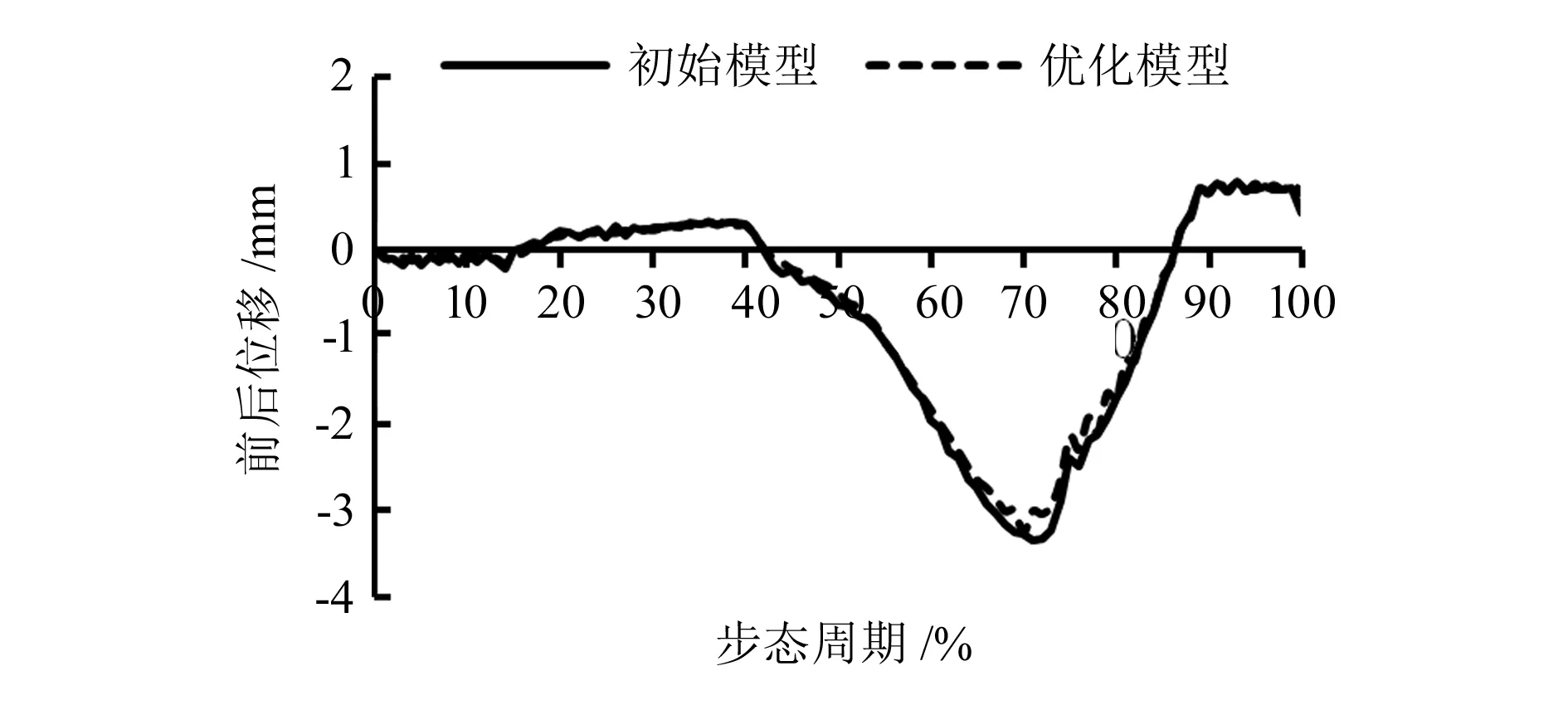
图10 整个步态周期胫骨衬垫前后位移对比

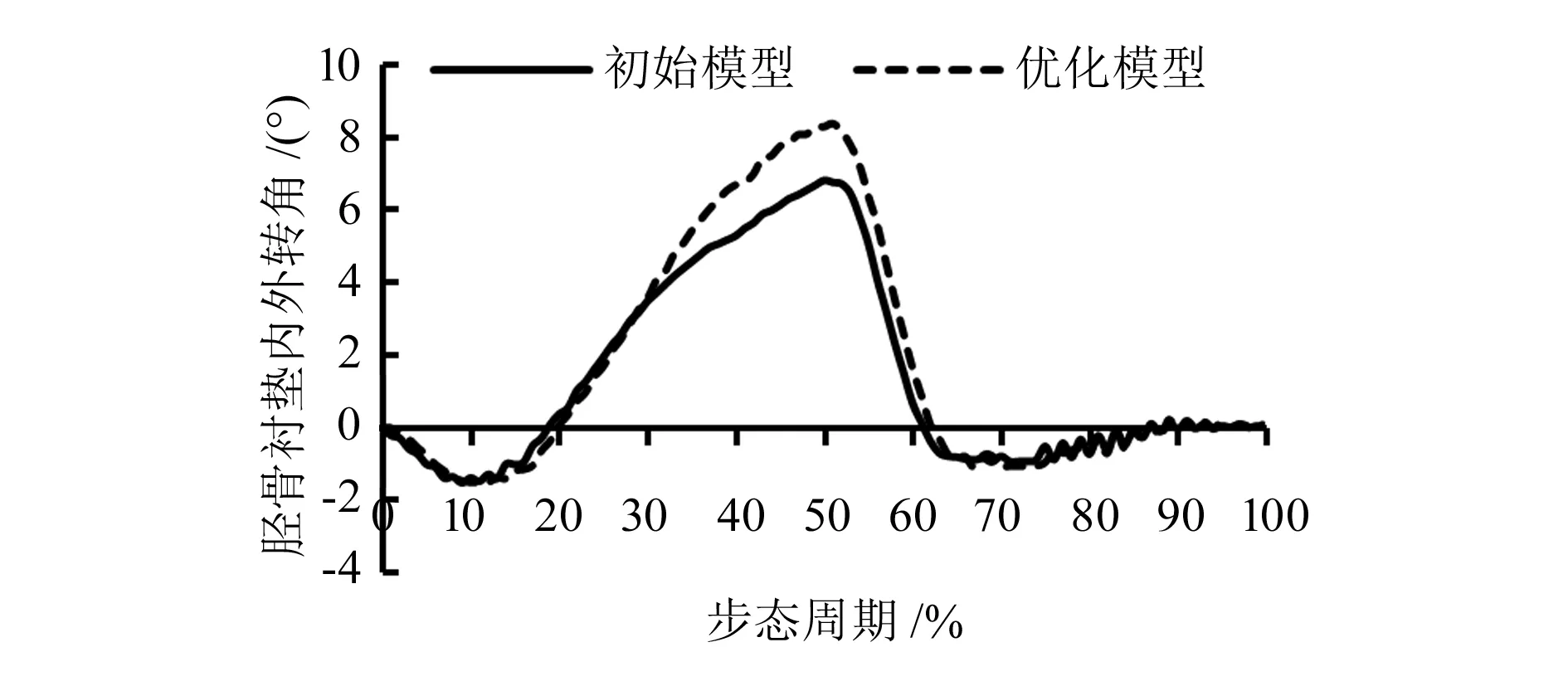
图11 整个步态周期胫骨衬垫内外转角对比