汽车动力总成悬置系统的多目标优化方法

姜立标，罗 健

(华南理工大学机械与汽车工程学院，广东 广州 510641)

汽车作为一种交通工具，其各项性能越来越受到人们的关注，其中整车NVH(noise、vibration、harshness)性能是目前人们关注较多的一项。影响整车NVH性能的因素有很多，动力总成的振动是其中一个重要的因素。动力总成的振动问题是复杂的多自由度振动问题。为使复杂的振动问题简单化，在设计悬置系统时，应对系统的解耦进行优化设计，并对动力总成的模态频率进行间隔设计。陈剑等[1]提出了基于Chebyshev区间的动力总成悬置系统优化方法，获得了较好的解耦率；毕凤荣等[2]提出了基于Kriging模型的动力总成悬置系统多目标优化方法，通过该模型得到了较好的解耦率。目前，对于动力总成悬置系统多目标优化多采用单一的方法或算法，优化效率较低。

为提高动力总成悬置系统的多目标优化效率，本文首先建立动力总成悬置系统模型，确定优化方向，基于算法融合理论，提出了结合多目标粒子群优化(multi-objective particle swarm optimization，MOPSO)算法和非支配排序遗传算法Ⅱ(non-dominated sorting genetic algorithm Ⅱ，NSGA-Ⅱ)的混合算法；然后进行了测试，证明了混合算法的效率更高且结果精度高；最后运用混合算法对具体的悬置系统进行优化，得到了准确的解集，为悬置系统提供了多组合理的设计参数。

1 动力总成悬置系统模型

1.1 运动学方程

以横置发动机三点悬置系统为研究对象，根据振动力学理论，建立系统的运动微分方程。图1所示为各坐标系下典型的动力总成三点悬置系统模型，图中G-XYZ是整车坐标系，O-xyz是动力总成坐标系，Ki-uvw是悬置局部坐标系。

图1 动力总成三点悬置系统模型

一般情况下，可以将动力总成简化为刚性体，在分析其动态特性时，假设悬置元件为无阻尼弹簧。将悬置系统简化为无阻尼振动系统，简化后运动方程为[3]:

(1)

式中：M为质量矩阵；K为刚度矩阵；X为动力总成坐标系下的位移列向量。

(2)

(3)

式中：m为动力总成的质量；Ixx,Iyy,Izz,Ixy,Ixz和Iyz为发动机的惯性参数；Pi为第i个悬置的位移矩阵；Ti为第i个悬置坐标系与整车坐标系的方向余弦矩阵；ki为悬置局部坐标系下的第i个悬置的刚度矩阵。

(4)

(5)

(6)

式中：xi,yi和zi为整车坐标系下第i个悬置的坐标；αui,βui和γui分别为第i个悬置的局部坐标轴ui与整车坐标系x,y和z轴的夹角；αvi,βvi和γui分别为第i个悬置的局部坐标轴vi与整车坐标系x,y和z轴的夹角；αwi,βwi和γwi分别为第i个悬置的局部坐标轴wi与整车坐标系x,y和z轴的夹角；kui,kvi和kwi为第i个悬置分别在局部坐标轴u,v和w方向上的刚度。

1.2 固有特性和能量解耦

1.2.1固有频率

将微分方程式(1)进行变换得到式(7)，对式(7)求解即可得到系统的固有频率。

(7)

式中：ωi为第i阶固有频率；φi为对应于ωi的特征向量。

1.2.2能量解耦率

能量解耦[4]也称模态解耦，所谓解耦就是使系统在各个方向的运动互不影响。假设系统是完全解耦的，则说明该系统某一方向上的运动不会引起其他方向上的运动，也就是各个方向的运动是相互独立的。

根据能量守恒定律，可以计算系统某一方向上的动能或势能占总能量的比，该比值即为解耦率。式(8)和式(9)中的T(l,i)分别表示按动能和势能计算的解耦率，结果是一致的。解耦率表达式如下：

(8)

(9)

式中：mlm为质量矩阵M中的第l行、第m列元素；klm为刚度矩阵K中的第l行、第m列元素；(φi)l和(φi)m分别为振型(φi)的第l和m个元素。

(10)

2 优化算法

各遗传算法都有其不同的优势和缺点，因此可以将多个不同的算法框架集成为一个算法框架来处理复杂的问题。这种混合算法通过特征交换来改善缺点，增加优点，具有更高的效率。本文采用MOPSO算法和NSGA-Ⅱ相结合的混合算法，将混合算法运用到动力总成悬置系统的多目标优化问题中，运用测试函数对其进行验证，结果证明该混合算法比单独的算法运算速度快，且结果准确。

2.1 MOPSO算法和NSGA-Ⅱ

MOPSO算法[5]是CoelloCoello C A等提出的用于多目标优化问题的一种优化算法。在粒子群算法中加入了拥挤距离，并以拥挤距离判断最优解。改进的粒子群算法能够以较快的收敛速度优化多个目标，并使每个目标都能较好地被满足，获得帕累托最优前沿(Pareto optimal front)。

NSGA-Ⅱ[6]为NSGA的升级版，是由K-Deb等人提出的在NSGA框架内加入了精英策略和快速非支配排序的一种新遗传算法，与NSGA相比，NSGA-Ⅱ运算速度更快，鲁棒性更好。

2.2 混合算法

本文将MOPSO算法和NSGA-Ⅱ相结合，组成混合算法。该混合算法采用并行育种方法，即初始种群同时在MOPSO算法和NSGA-Ⅱ中产生，然后将两个独立的种群混合在一起，合并后的新种群同时在两种算法中迭代，并生成下一代混合种群，如此重复，直到满足条件退出算法。采用并行育种的混合方法，可以产生更广泛的种群，使算法在区域间具有广泛的搜索策略，同时使搜索过程更加收敛，使结果更加准确。混合算法的流程如图2所示。

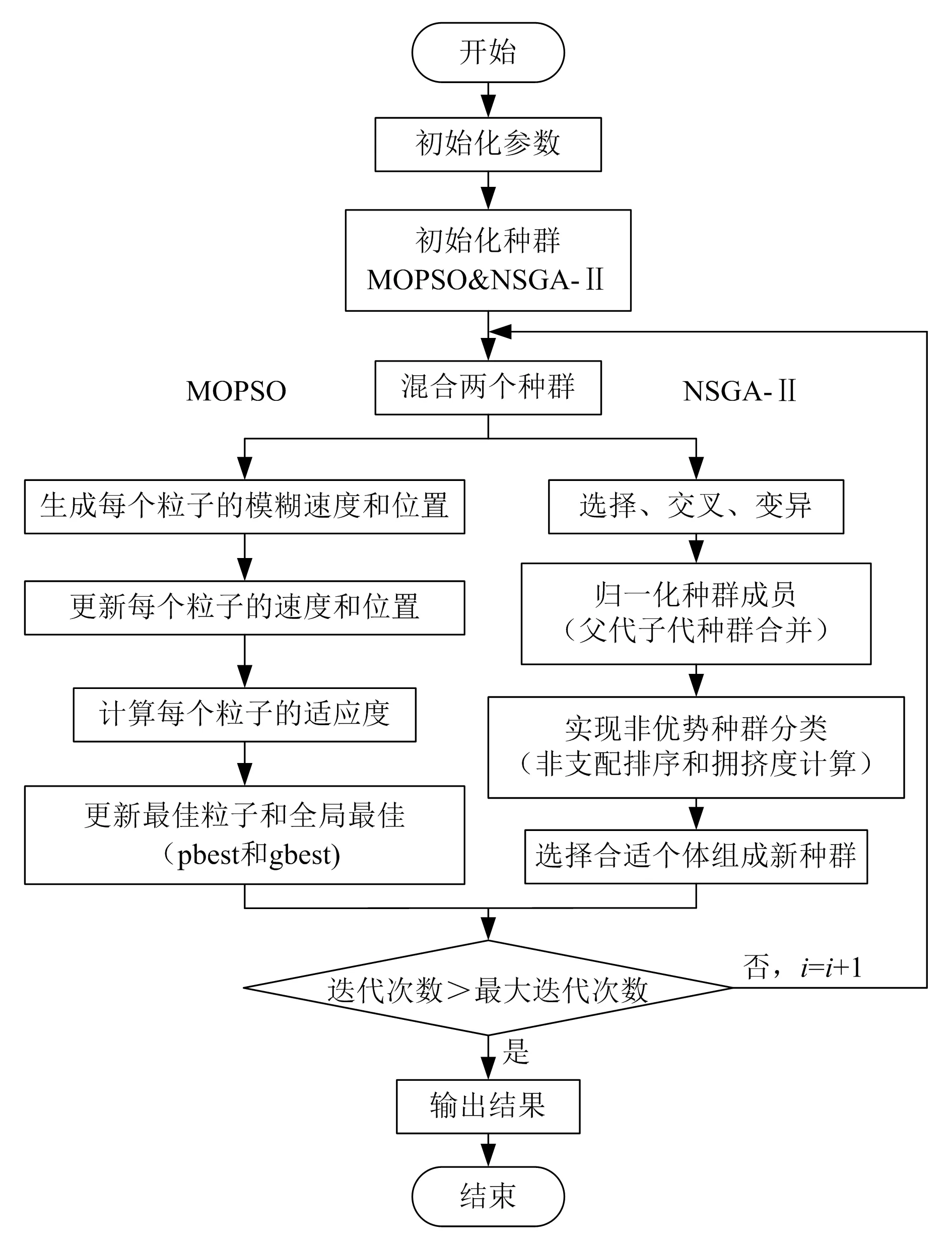
图2 MOPSO算法和NSGA-Ⅱ混合算法流程图

2.3 结果分析

对混合算法进行了测试，测试函数分别选用ZDT1、ZDT3和DTLZ2，同时测试了不同算法对不同测试函数的计算时间。为了减少测试时产生的误差，将每种算法的计算次数均设为10 000次。图3所述为不同算法的计算时间，由图可以看出，混合算法大大缩短了计算时间，比单独使用NSGA-Ⅱ和MOSPO算法具有更高的效率。图4所示为MOPSO&NSGA-Ⅱ混合算法对测试函数ZDT1、ZDT3、DTLZ2的仿真结果，从图中可以看出，混合算法可以很好地求出每个基准点上的帕累托最优解，图4中“*”散点集即为帕累托最优解集。

图3 不同算法的计算时间

3 动力总成悬置系统的多目标优化

进行多目标优化[7]一般需要明确优化变量、建立目标函数以及设置约束条件。本文以动力总成悬置系统的解耦及模态间隔为优化对象，建立目标函数，悬置静刚度作为优化变量，静刚度的上下限设为约束条件。

3.1 优化变量

一般将设计变量作为优化变量，悬置系统的设计变量包括设计参数和布置参数。悬置的静刚度和阻尼属于设计参数，改动的可能性较大，而布置参数一般随总成而确定，改动机会很小，因此通常将悬置的静刚度作为优化变量。优化变量[8]x可以写成：

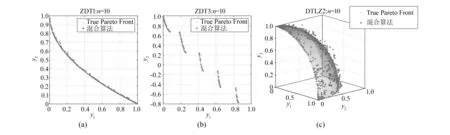
图4 混合算法测试结果

x=[kui,kvi,kwi]T

(11)

3.2 目标函数

动力总成悬置系统的设计要求是保证刚体模态在合理的频率范围内，且各模态频率间满足一定的间隔要求，同时满足各个方向的解耦目标。结合实际要求建立多个目标函数如下：

(12)

式中：fn为第n阶主方向解耦率的目标函数；f7为纵向和垂向模态间隔最大值的目标函数；f8为纵向和俯仰模态间隔最大值的目标函数。

3.3 约束条件

约束条件指的是对目标函数中设计变量的限制条件。根据悬置结构及实际制造工艺，对优化变量悬置静刚度设置上下限。悬置静刚度的约束条件表示为：

kuil≤kui≤kuiu

kvil≤kvi≤kviu

kwil≤kwi≤kwiu

(13)

式中：kuil和kuiu分别为第i个悬置u向刚度值的下限和上限；kvil和kviu分别为第i个悬置v向刚度值的下限和上限；kwil和kwiu分别为第i个悬置w向刚度值的下限和上限。

3.4 优化实例

3.4.1参数输入

研究的实例对象是动力总成三点悬置系统，动力总成参数及优化前悬置的相关参数见表1～表3。

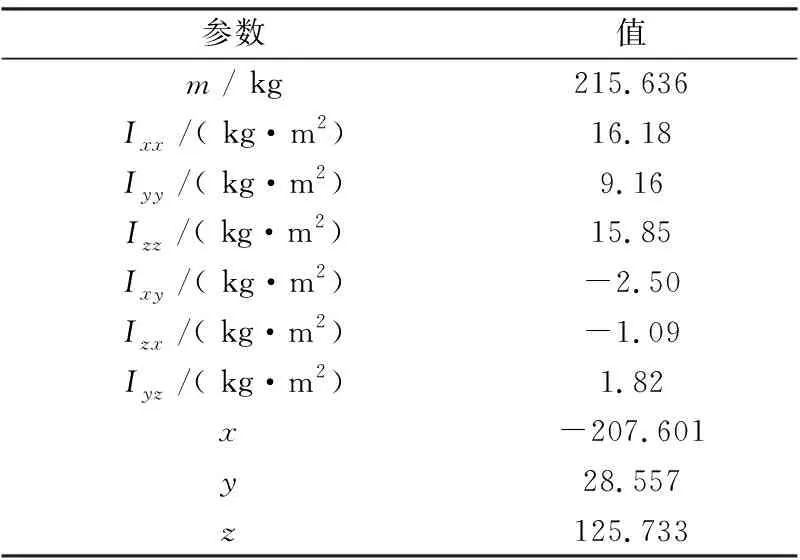
表1 动力总成参数

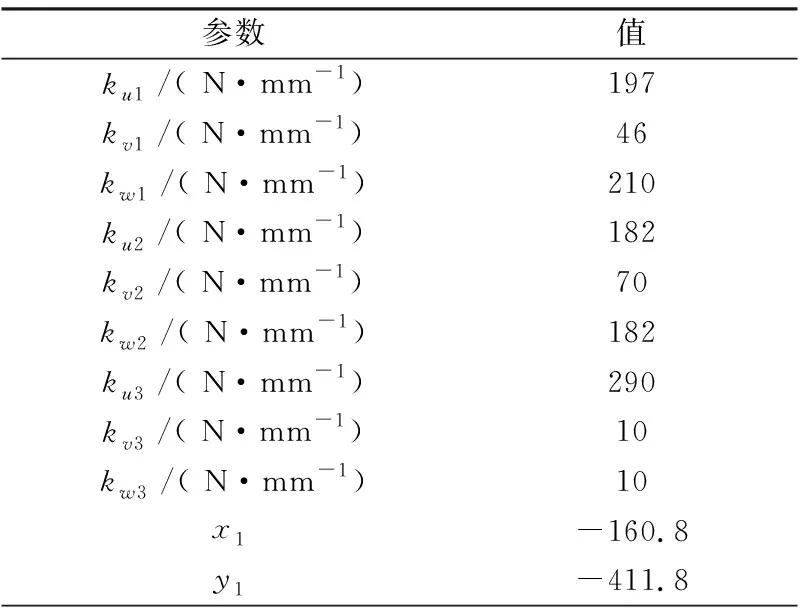
表2 悬置优化前参数

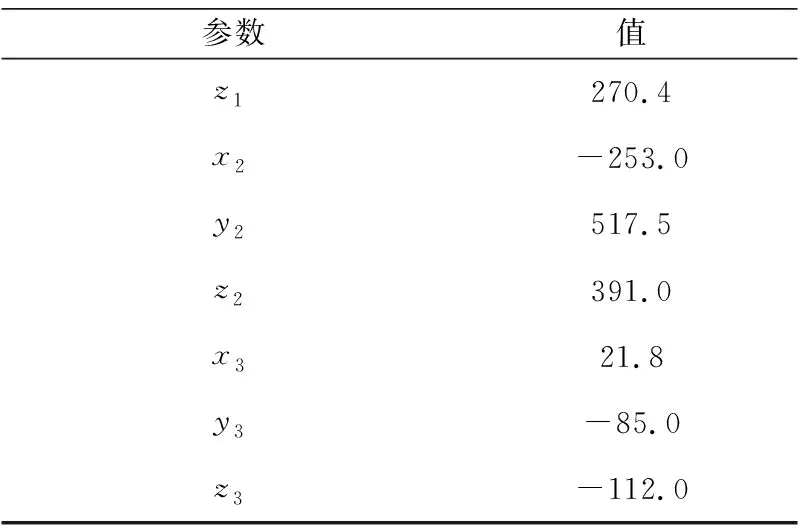
续表

表3 悬置安装角度 单位：(°)

3.4.2优化结果

根据第2节提出的混合算法，对动力总成悬置系统进行优化，得到了满意的结果，优化后的悬置静刚度值详见表4。

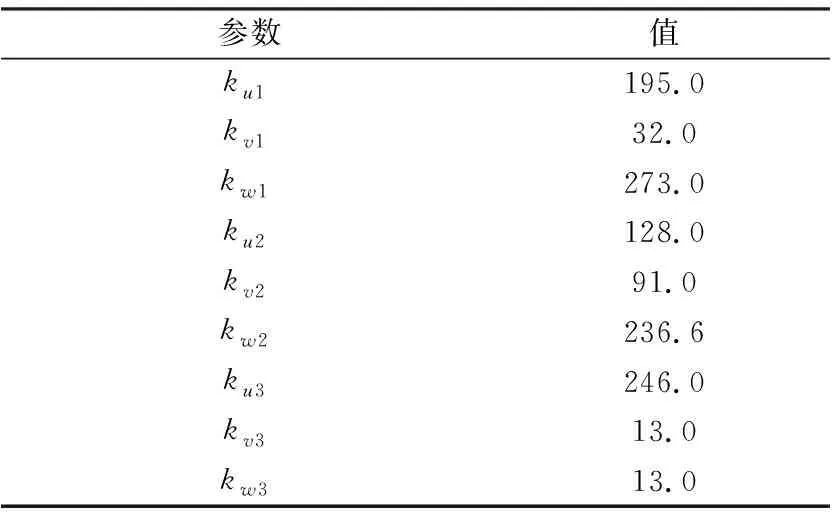
表4 优化后各悬置静刚度值 单位：N·mm-1

表5是优化前和优化后的结果对比，由表可以看出，优化后的悬置静刚度使系统的解耦率满足要求，较优化前的解耦率有了显著的提升，动力总成系统的纵向和滚转两个方向的解耦率分别较优化前提高了13%和49%。

表5 优化前后的模态频率和解耦率

图5所示为各悬置静刚度的帕累托最优解集，由图可知，均满足目标函数。说明通过该优化方法，可以为悬置系统设计提供多组方案，再根据实际的制造工艺和结构选择其中一组作为悬置的设计方案。

4 结束语

通过对汽车动力总成悬置系统的建模和理论分析，确定了影响动力总成刚体模态与系统解耦率的相关参数，为悬置系统的优化指明了方向。将MOPSO算法和NSGA-Ⅱ相结合，形成了更加高效的混合算法，并将其运用到了动力总成悬置系统的优化上，结果表明，优化后的结果较优化前有了很大的提高，优化后动力总成悬置系统6个方向的解耦率均满足设计要求，验证了该混合算法用于求解动力总成悬置系统多目标优化的有效性。通过该算法得到了多组解集，为实际的制造工艺和结构提供了多种选择。

图5 各悬置静刚度的帕累托解集