含变质量负载的双连杆机械臂振动控制*

马驰骋 胡帅钊 高坤明 张春林 郭宗和†

（1.山东理工大学交通与车辆工程学院，淄博255000）（2.中南林业科技大学土木工程学院，长沙410004）

引言

柔性机械臂结构在工业自动化或者智能装备等领域的普及率越来越高，有效地提高了工业生产效率.在机械臂工作过程中，构件的刚体运动或者操作对象的质量变化都会引起结构整体参数的改变.关于含变质量构件的旋转运动结构的动力学问题研究开展得相对较少，而在工业机器人、建筑机械、空天大型柔性结构及荷载机械臂等实际工程问题中，又迫切地需要开展变质量-刚柔耦合系统的动力学响应及其振动主被动控制方面的科学研究［1］.曹青松等［2，3］针对刚-柔-电耦合的双连杆压电柔性机械臂，结合模糊自整定/PSO自整定算法提高PID控制器的作用效果，仿真和实验表明混合PID控制器具有响应快、鲁棒性好、调整方便等优点，更好地改善了控制系统的动态性能.洪昭斌等［4］设计了基于奇异摄动理论的载体、关节铰轨迹跟踪的鲁棒神经网络控制算法和柔性振动反馈PD控制算法，所设计的控制算法解决了系统参数未知等因素带来的影响，能快速准确地追踪运动轨迹，同时可以抑制柔性杆的振动模态.空间机械臂系统在转动过程中必然会激起柔性臂的弹性振动，娄军强等［5，6］在降低伺服电机的驱动扭矩的同时，通过反馈策略抑制了柔性臂的弯曲和扭转振动，从而提高了柔性机械臂系统的末端定位精度.

近年来机器人工业的蓬勃发展，进一步推动了刚柔耦合结构振动控制方面的研究.Mohamed Z等［7］提出了一种基于线性矩阵不等式（LMI）的比例微分（PD）耦合控制器，用来实现平面双连杆柔性机械毂角位置和端点偏转控制，从输入跟踪能力和臂杆偏转水平两方面评价了该控制器的性能，实验结果表明LMI-PD控制具有更好的鲁棒性和系统性能.Lochan K等［8］针对一种双连杆柔性机械臂结构，通过一种基于PID滑面的滑模控制器，实现了目标的高精度滑模控制，并利用李雅普诺夫稳定性理论，保证了PID滑动面的稳定性.荣吉利等［9］建立了刚柔耦合的双连杆机械臂动力学模型，提出了一种LQR-PD联合控制策略，不仅能实现关节轨迹的精确跟踪，而且能有效抑制臂杆末端的残余振动.针对系统的不确定性和时变扰动，Xu B［10］分别提出了基于复合学习控制和基于扰动观测器的两种性能增强型控制器，有效地提高机械手的跟踪性能.Karagülle H等［11］主要分析了伺服电机加减速时间和双连杆结构残余振动的关系，发现如果减速时间的倒数等于系统的第一阶固有频率时残余振动（均方根）最小；如果减速时间的倒数等于第一阶固有频率的一半，残余振动最显著.Gao H等［12］本文采用假设模态法建立了两连杆柔性机械手的N维离散化模型，然后基于离散化的动力学模型和神经网络控制器，研究了全状态反馈控制和输出反馈控制，实现了轨迹跟踪和振动抑制，并设计实验平台验证了该神经网络控制器的可行性.邱志成等［13］以两杆柔性机械臂实验平台为基础，对柔性臂转动过程中由于电机力矩驱动产生的弹性振动，采用比例控制和非线性控制算法进行振动主动控制，取得了优良的控制效果.Qiu Z等［14］采用广义最小方差自校正控制和基于Takagi-Sugeno模型的模糊神经网络控制方案，对两连杆柔性机械手的主动振动控制进行了实验研究，结果表明与传统的线性PD控制器相比，所设计的控制器能更快地抑制双连杆柔性机械手的大振幅和小振幅振动，特别是小振幅残余振动.杜严锋等［15］对柔性机械臂系统建立了一次近似刚柔耦合动力学模型，针对不同的运动参数对系统振动变形情况进行了仿真，分析了减速时间对机械臂残余振动的影响.从文献回顾中可以发现，近年来关于柔性机械臂的动力学分析、定位追踪和振动控制等方面的研究工作越来越多，然而旋转机械臂工况下质量变化对系统动力学特性的研究仍然相对缺少.

在之前工作的研究基础上［16-18］，针对含变质量负载的双连杆机构，本文主要开展了动力学响应分析和振动主动控制两个方面的工作，具体内容如下：推导了变质量-双连杆结构的有限元方程，研究了负载质量恒定系统和负载质量时变系统的振动特性，最后采用速度比例负反馈控制器对含变质量负载的双连杆结构进行了振动控制.

1 有限元模型

含变质量构件的双连杆结构如图1所示，弹性杆OA和杆AB都可以自由旋转，固定端O和连接A处分别安装一个伺服电机，杆AB的末端有一个质量负载，末端集中质量是时间的函数，定义为m（t）.两根杆的角度历程如图2所示，两个电机先加速，然后平稳运动，最后减速达到指定位置.然而由于杆件属于弹性体，电机停止工作后，惯性使弹性杆件产生残余振动.这也是在实际中不希望出现的情况，因为残余振动会影响结构的定位和工作稳定性，因此有必要对残余振动现象分析并加以控制.在推导结构的动力学方程之前，首先对一个变质量弹簧振子系统进行分析，系统的刚度和质量分别是k和m（t），位移用x表示，那么系统的动能和势能分别为1/2mẋ2和1/2kx2，根据拉格朗日方程可以得到系统的运动微分方程为mẍ+ṁẋ+kx=0，从方程中可以看出方程中第二项是质量变化率和速度的乘积，类似于一个阻尼的作用.因此在变质量系统的动力学分析中，质量变化会同时引起惯性项和阻尼项的改变.更为重要的是当系统质量减少时，质量变化率小于零，此时阻尼项为负，负阻尼会减缓振动的衰减，当该项大于结构阻尼时，甚至会引起振动的放大.在后面的推导中，附加的阻尼项被直接加在对应的节点上.电机O、电机A和末端负载的质量分别用m1、m2和m3表示，电机O和电机A等效刚度用k1和k2表示.

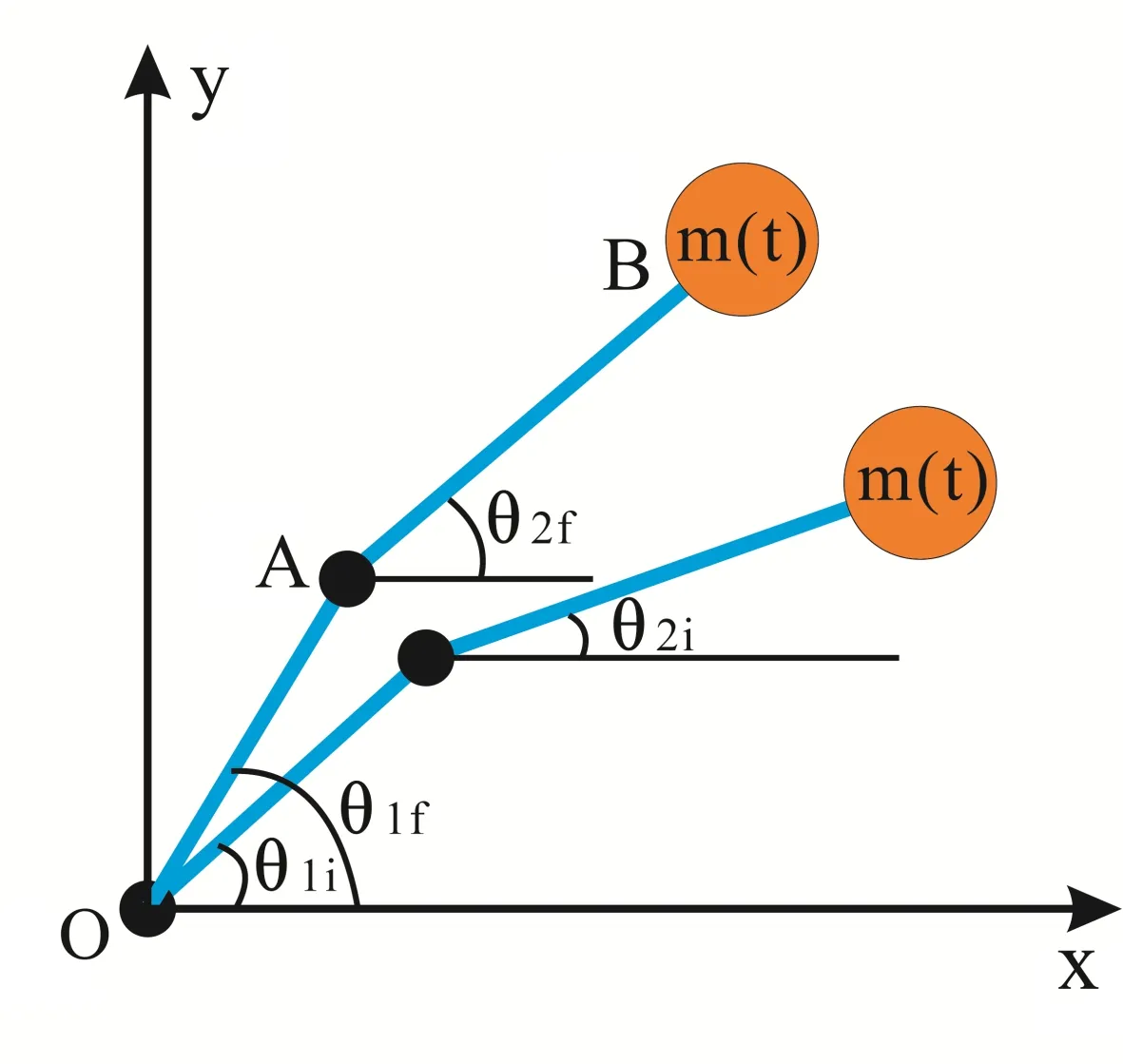
图1含变质量负载的双连杆机构Fig.1 Double link mechanism with variable mass load

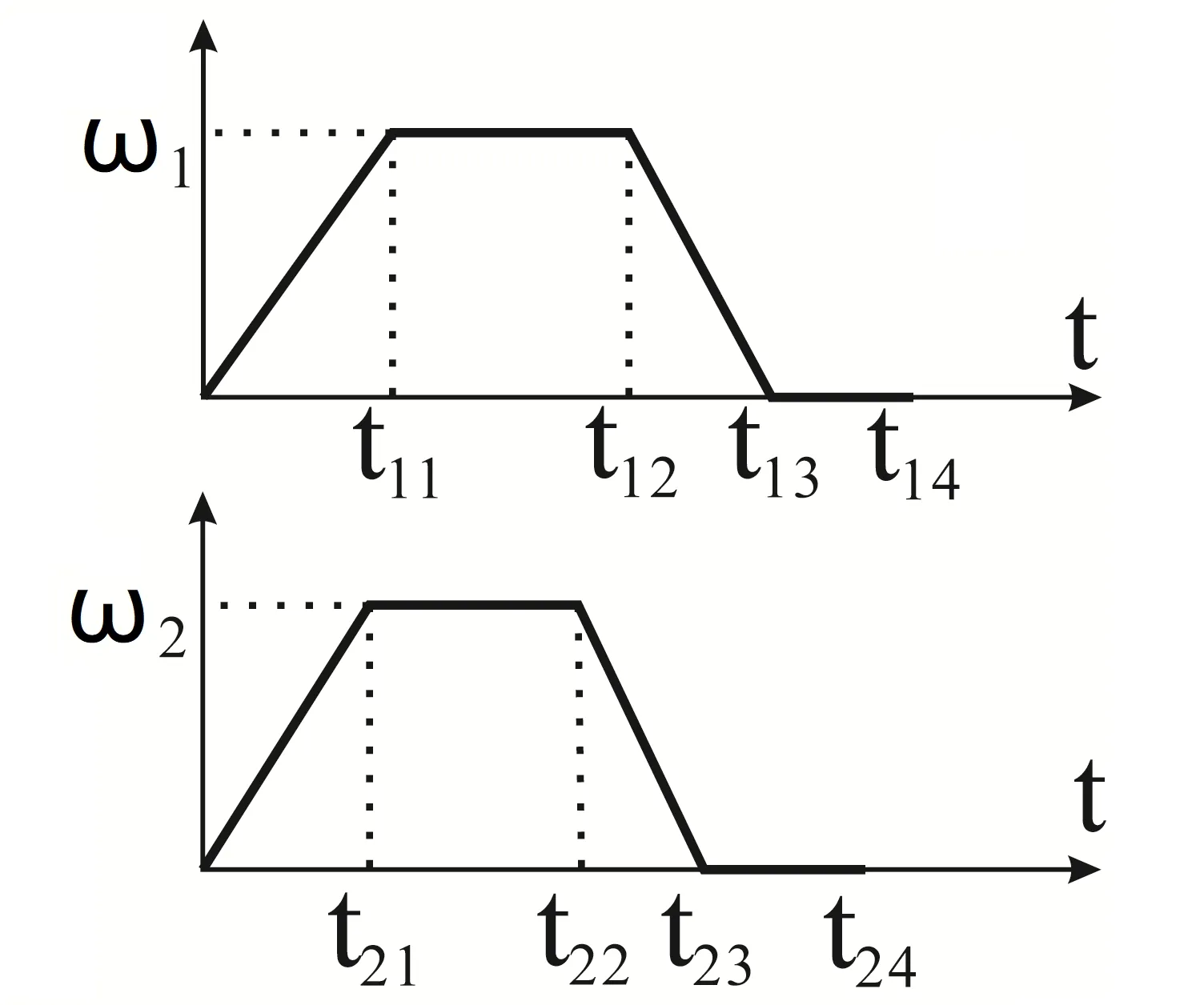
图2角速度历程Fig.2 Angular velocity history

根据有限单元法［19，20］，可以方便地建立图1所示结构的动力学方程.采用平面梁单元（2节点）建立杆件的有限元模型，每个节点包含三个自由度，包括两个位移自由度（u，v）和一个转角自由度φ：单元位移可以通过形函数N和节点位移di来表示：同时需要一个转换矩阵来描述杆件单元的节点位移，转换矩阵T具有如下形式，

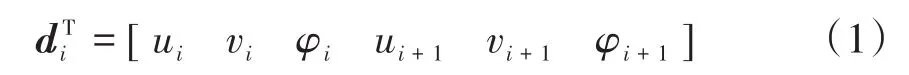
其中，

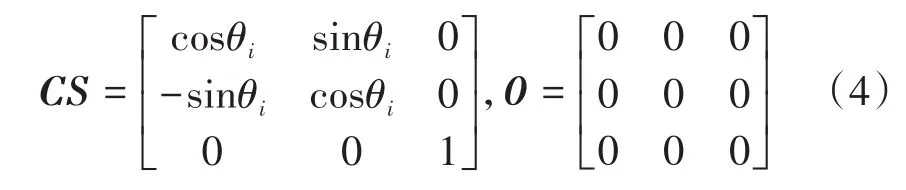
利用转换矩阵T，任意角度处的第i个单元的位移向量d，刚度矩阵k，质量矩阵m和外力向量f都可以通过转换矩阵来表示，

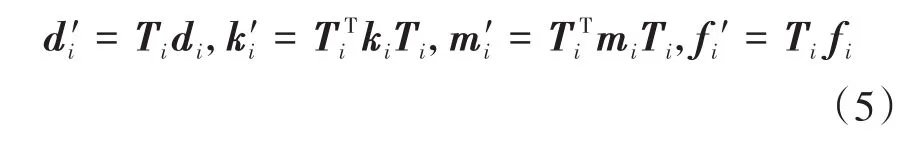
其中，ki和mi为梁单元的单元刚度矩阵和质量矩阵，fi为单元惯性载荷向量，具体形式为［11］：

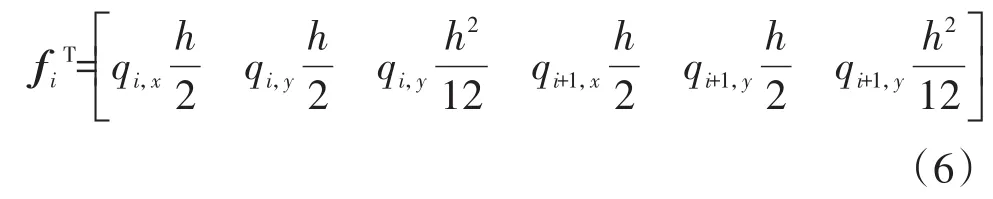
其中，h为单元长度，杆件单位长度的重量为ρA，x和y方向的由电机驱动引起的加速度分别为ax和ay，那么x和y方向的惯性力分量分别为qix=-ρiAihax和qiy=-ρiAih(ay+g)［11］，其中g为重力加速度.将转换后的单元刚度矩阵进行组装，得到系统整体的运动方程为：

其中M，C，K和F分别为总体质量矩阵、总体阻尼矩阵、总体刚度矩阵和载荷向量.阻尼C为比例阻尼，用比例阻尼系数α和β表示，

因为伺服电机具有一定的刚度k1，因此，O点处（矩阵中nO位置）的刚度为：

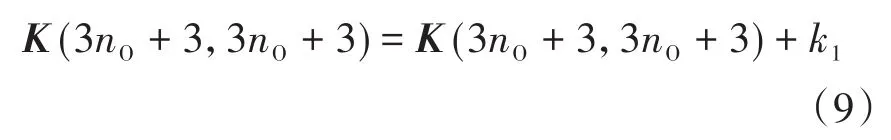
在A点处（矩阵中nA位置）我们需要考虑伺服电机的质量m2和转动惯量I2，质量矩阵修改为：

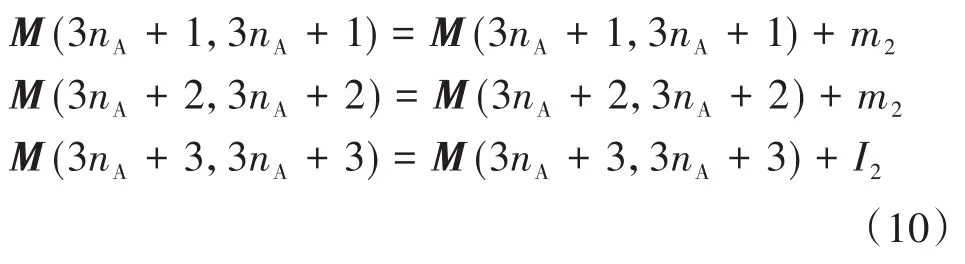
同时还要考虑伺服电机2的刚度k2，刚度矩阵在nA修改为，

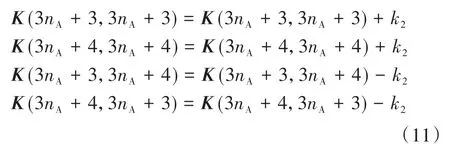
在B点（矩阵中nB位置）忽略末端负载对刚度的影响，只考虑集中质量m3对系统总体质量矩阵的影响：

根据前面的介绍已知质量变化会引起一个附加的阻力项［16-18］，这个阻尼并不是传统意义上的阻尼，而是因为力与速度成正比，我们把他定义为一个阻尼项，大小为质量对时间的导数.

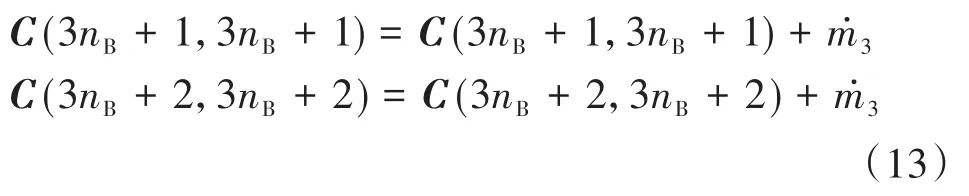
2 动力学特性分析

双连杆结构中杆OA和杆AB的材料参数如表1所示，伺服电机的质量、转动惯量以及刚度系数在表2中列出［11］.

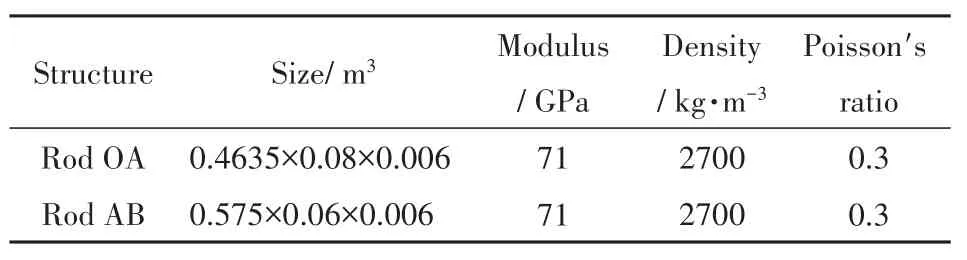
表1 材料参数Table 1 Properties of the material

表2 伺服电机参数Table 2 Parameters of the Servo motors

使用表1和表2中的参数计算系统的前四阶模态和对应的固有频率.前四阶模态如图3所示.表3中列出了不计末端负载时两根杆夹角不同时结构的固有频率（θ12=θ2f-θ1f），从表中可以看出，随着两根杆夹角角度的增大，第一阶固有频率逐渐增大，这是由于对于第一阶模态是绕着左端电机的变形，结构重心越靠近左端，有效质量越小，从而频率越高.第二阶模态以杆AB的变形为主，同时随着角度的增大，杆OA对杆AB的影响减小，即杆AB的约束变弱，从而导致第二阶频率降低.从表中也可以看出夹角的变化对高阶频率影响较小.表4中列出了θ12=90∘时不同末端负载时结构的固有频率，质量越大，固有频率越低.对于旋转机械臂来说，由于刚体运动和负载质量的改变，系统的振动频率发生明显的改变，残余振动的响应规律也更加复杂，这进一步增加了振动控制的难度.

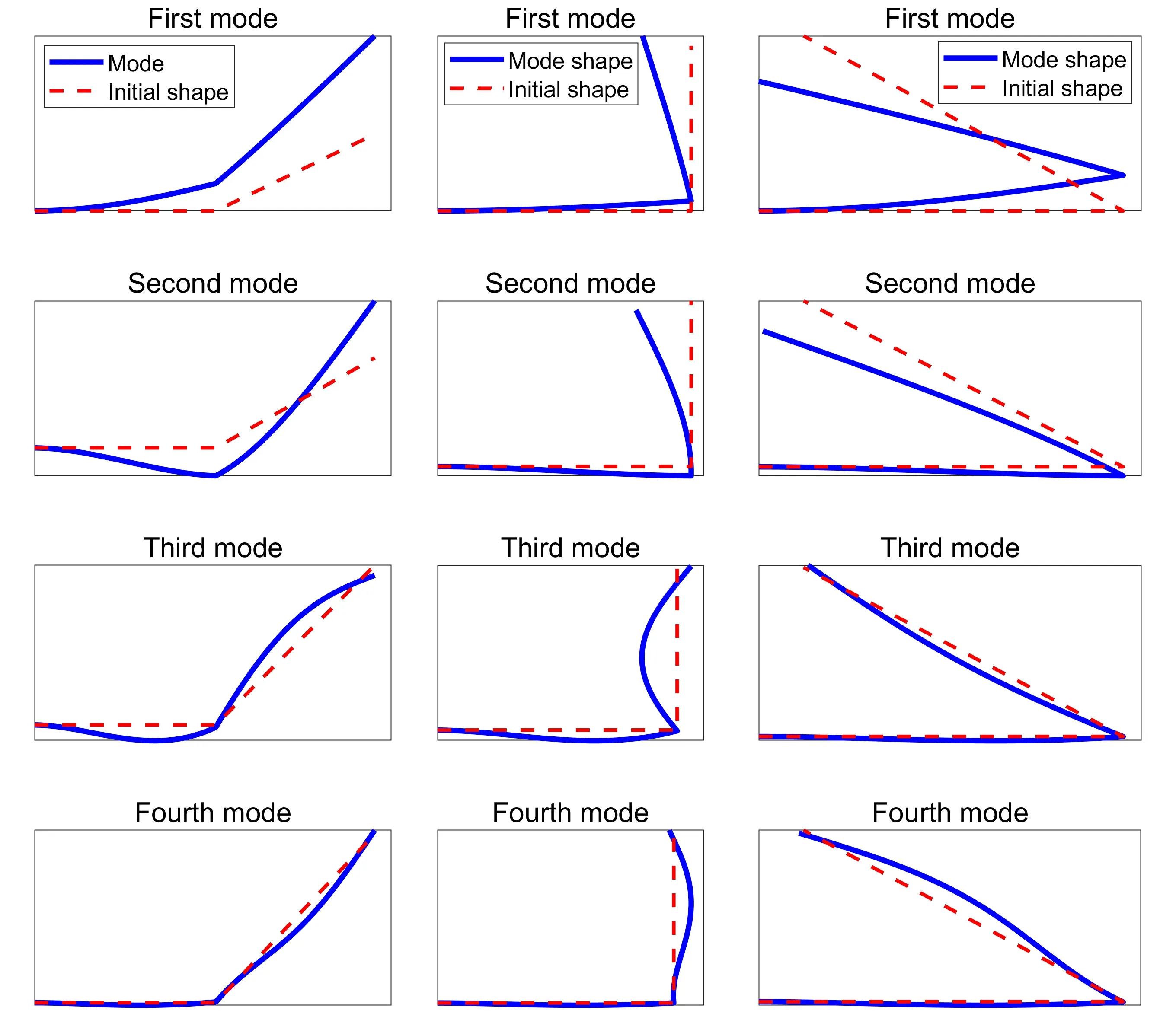
图3 不同θ12时结构的振型Fig.3 Mode shapes for different θ12

表3 不同角度时结构的固有频率Table 3 Natural frequencies of the structure with different angles

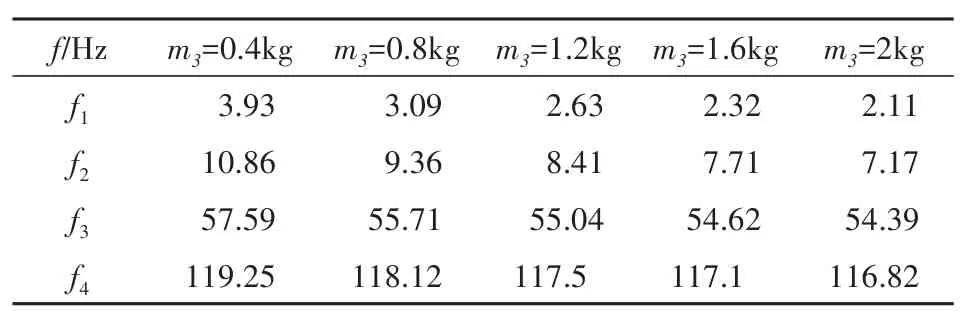
表4 不同末端负载时结构的固有频率Table 4 Natural frequencies of the structure with different payloads

在本文中只研究了一种典型的运动模式如图4所示，其他模式可以从这种模式上拓展.开始时两根杆在同一直线上，电机O和电机A分别带动杆OA和杆AB旋转，经过一段时间后，杆OA旋转了90°，杆AB旋转了170°.两根杆从初始位置到最终位置角度的变化如图5所示，3s后电机停止工作，但是由于惯性的影响，两根杆还会发生振动，经过一段时间的衰减，杆件才能准确地停到指定位置.实际工作中机械臂往往需要完成连贯的动作，因此残余振动会严重影响机械臂的定位和运动稳定性.

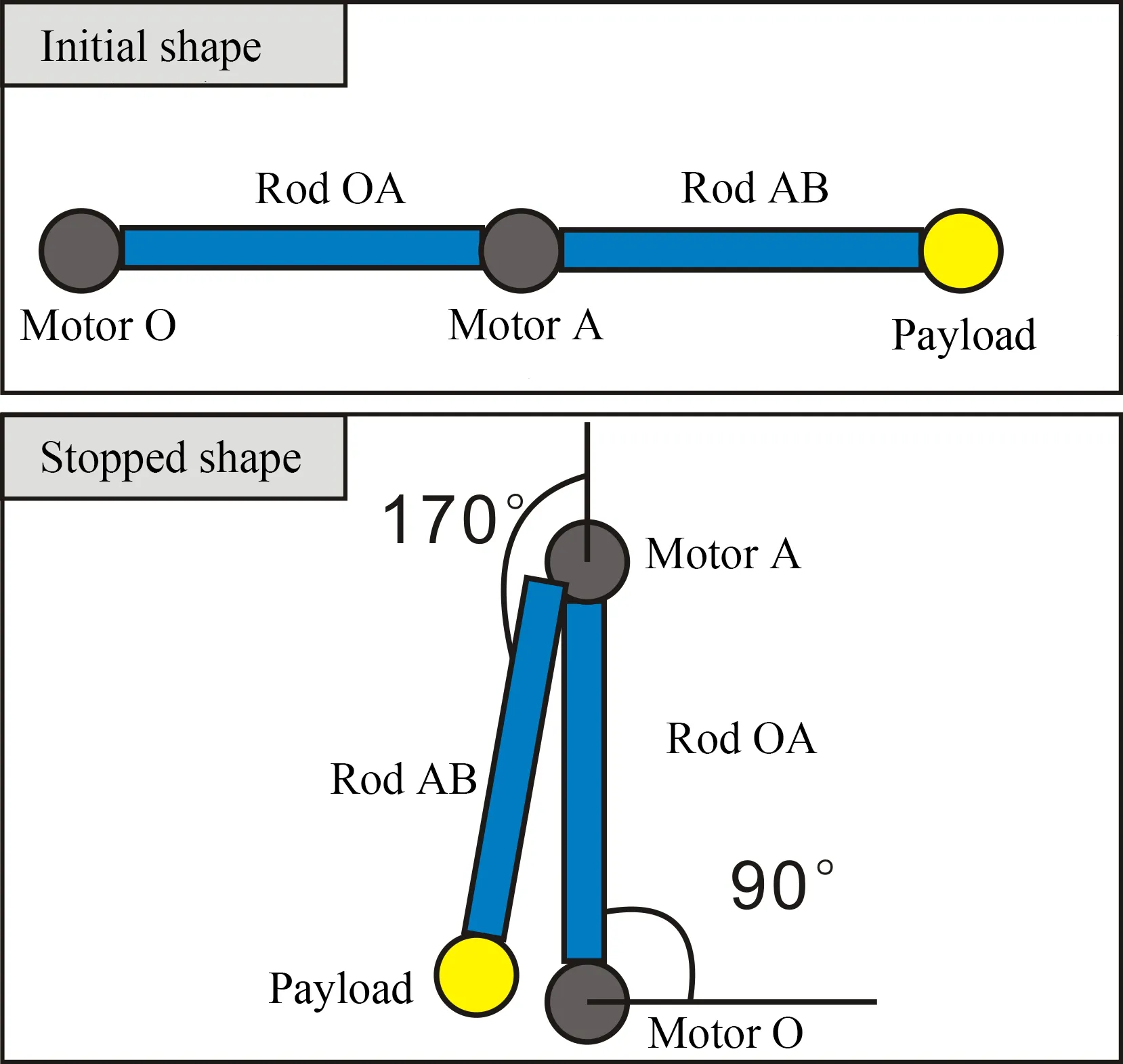
图4 双连杆结构的运动状态Fig.4 The motion state of the double-link structure

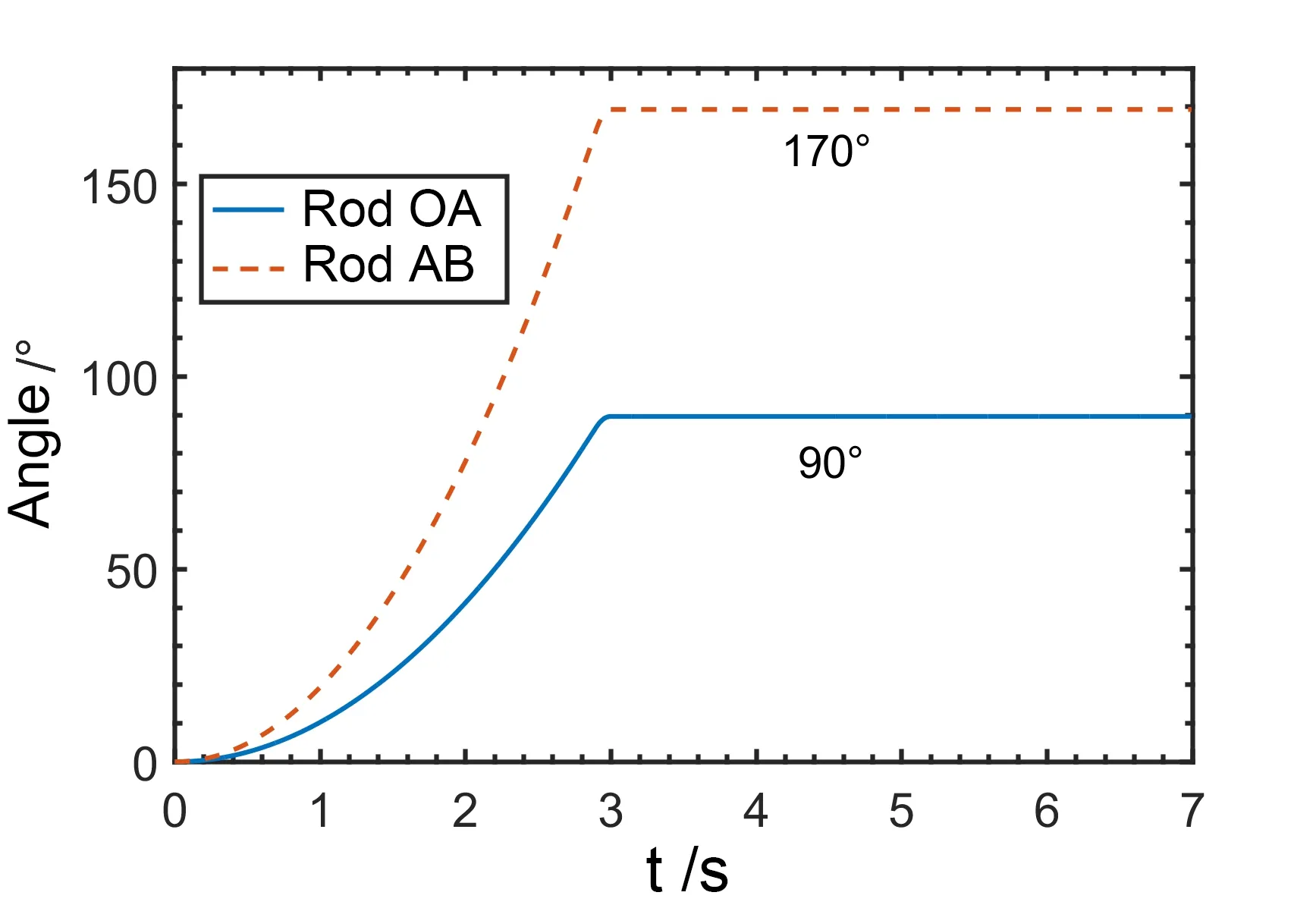
图5 两根杆件的旋转角Fig.5 Rotation angle of two rods

通过Bathe法［20］求解系统的有限元方程（6），计算流程如图6所示.计算中时间步长为0.007s，比例阻尼系数分别取1%和0.1%.图7给出了负载质量不变时系统的加速度响应，图7（a）是负载质量等于0.4kg时系统的响应，图7（b）是负载质量等于2kg时系统的响应.从图中我们可以看到，当结构停止旋转时，杆件依然会发生剧烈的振动，也就是说发生了残余振动，一方面负载质量越大，系统的频率越低，另一方面也可以看到负载越大，惯性越大，因此残余振动也越明显.

图6 Bathe法计算流程Fig.6 The flow chart of the Bathe’s method

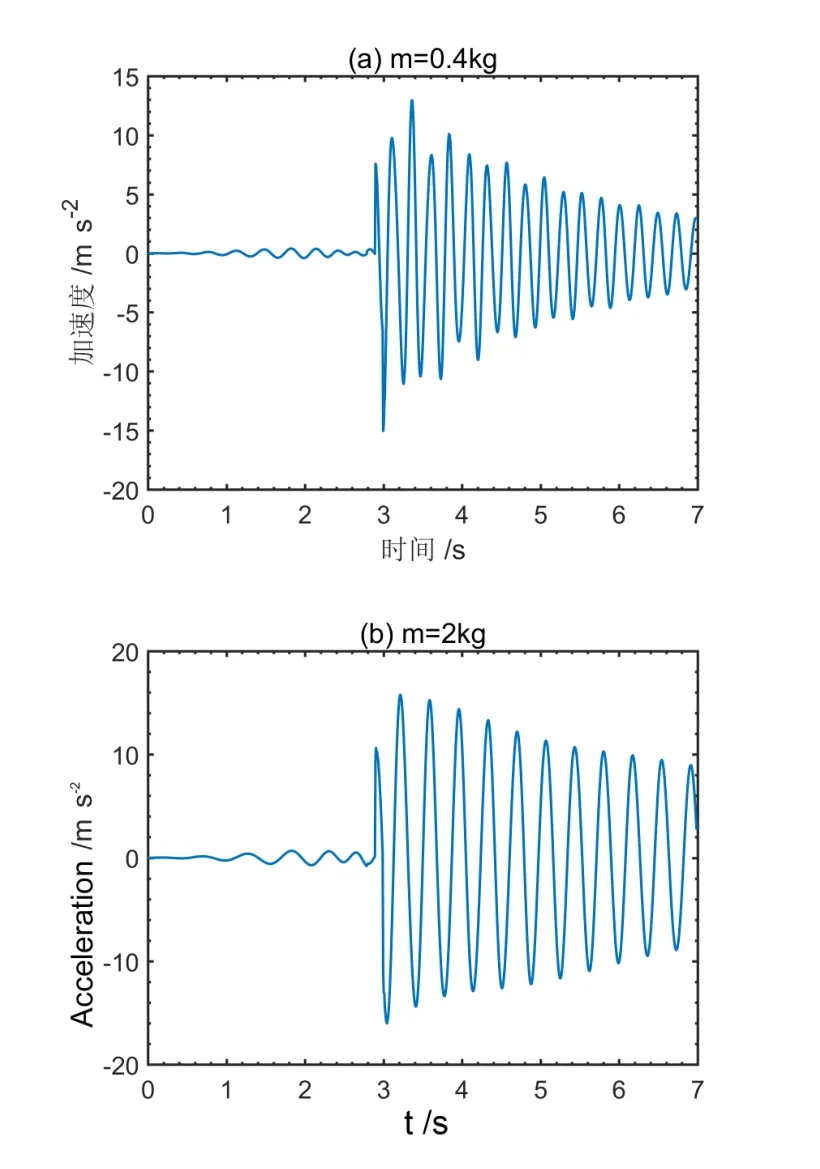
图7 负载质量恒定时系统自由端的加速度响应曲线Fig.7 Acceleration response curves of the free end of the system with a constant payload

图8显示了负载质量变化时系统的加速度响应曲线，在质量增加和质量减小两种情况下系统响应分别如图8（a）和图8（b），在质量增大过程中，负载质量从0.4kg增大到2kg，质量减小过程中，负载质量从2kg线性减小到0.4kg.关于变质量负载的问题，在航天航空领域研究比较广泛，但是在以往的研究中重点分析了质量变化对系统固有频率特性的影响，而并没有考虑质量变化引起的附加阻尼的效果，因此本文同时给出了考虑附加阻尼和不考虑附加阻尼两种情况时系统的响应，如图8所示.从图中可以明显看出，附加阻尼对系统的响应影响是非常显著的.当系统质量增加时，会产生一个附加的正阻尼，因此系统的响应会在正阻尼的作用下加速衰减，而在质量减小过程当中，会同时引起一个附加的负阻尼力，这个负阻尼力会减缓系统振动的衰减.如果系统的质量变化非常剧烈，那么会引起一个很大的附加阻尼作用，当附加的阻尼力的作用超过结构本身的阻尼时，甚至会引起系统振动幅值的增大.因此在变质量结构动力学分析中，系统质量变化引起的非结构阻尼作用十分显著，质量变化引起的非结构阻尼效应不可忽略.

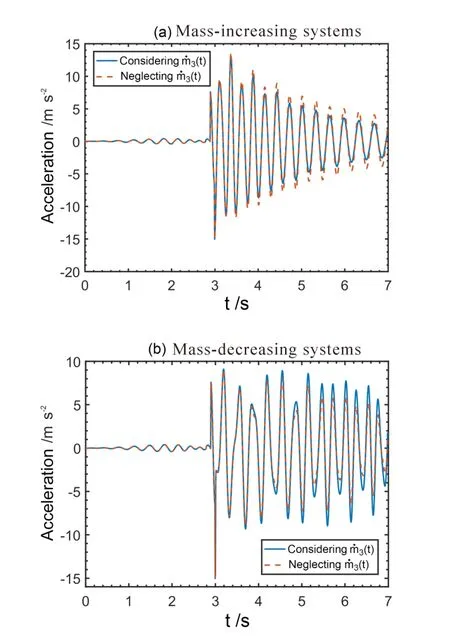
图8 负载质量变化时系统自由端的加速度响应曲线Fig.8 Acceleration response curves of the free end of the system with a time-varying payload

3 主动控制研究

在杆AB上靠近电机A的位置粘贴PZT-5A压电片，利用压电致动效应产生反馈控制力，压电片的尺寸为30*20*0.5 mm3.设计速度负反馈控制器开展结构的主动控制研究，首先采集自由端处的加速度，通过积分模块将加速度量转换成速度量，由反馈控制器输入信号给功率放大器，最后驱动压电致动器实现闭环控制.

首先仿真了负载质量恒定时双连杆结构的残余振动抑制，控制前后系统自由端附近的加速响应曲线如图9所示，从图9中可以看到，对于m=0.4kg和m=2kg两种负载工况下，施加反馈控制之后，系统的响应得到了有效的抑制.在压电片的工作电压范围内，增大反馈系数可进一步提升控制效果.

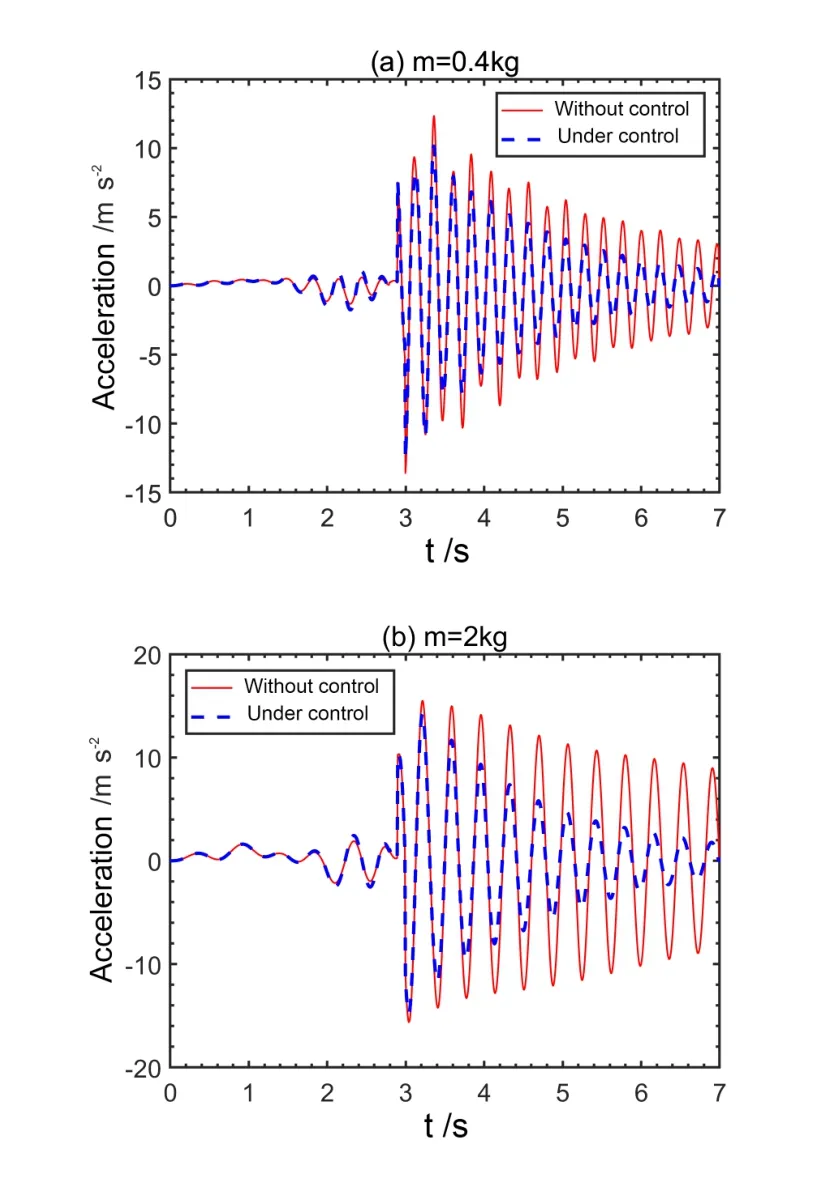
图9 负载质量恒定时的控制效果Fig.9 Control results for the system with constant payload

然后对含变质量负载的双连杆机构开展数值模拟，负载质量仍然从0.4kg线性增大到2kg，或从2kg线性减小到0.4kg，在质量增大工况和质量减小工况下控制结果分别如图10（a）和图10（b）所示.根据控制前后杆件自由端处的加速度响应对比，可以明显看出施加反馈控制后，结构的振动幅值迅速衰减，说明了速度反馈策略对时变参数系统控制的有效性，由于质量减小系统的速度响应较大，因此控制效果更佳显著.根据响应对比，还有很大的控制提升空间，一方面可以增大反馈系数，另一方面可以尝试采用高级控制算法，如模糊PID控制，最优二次型控制等.

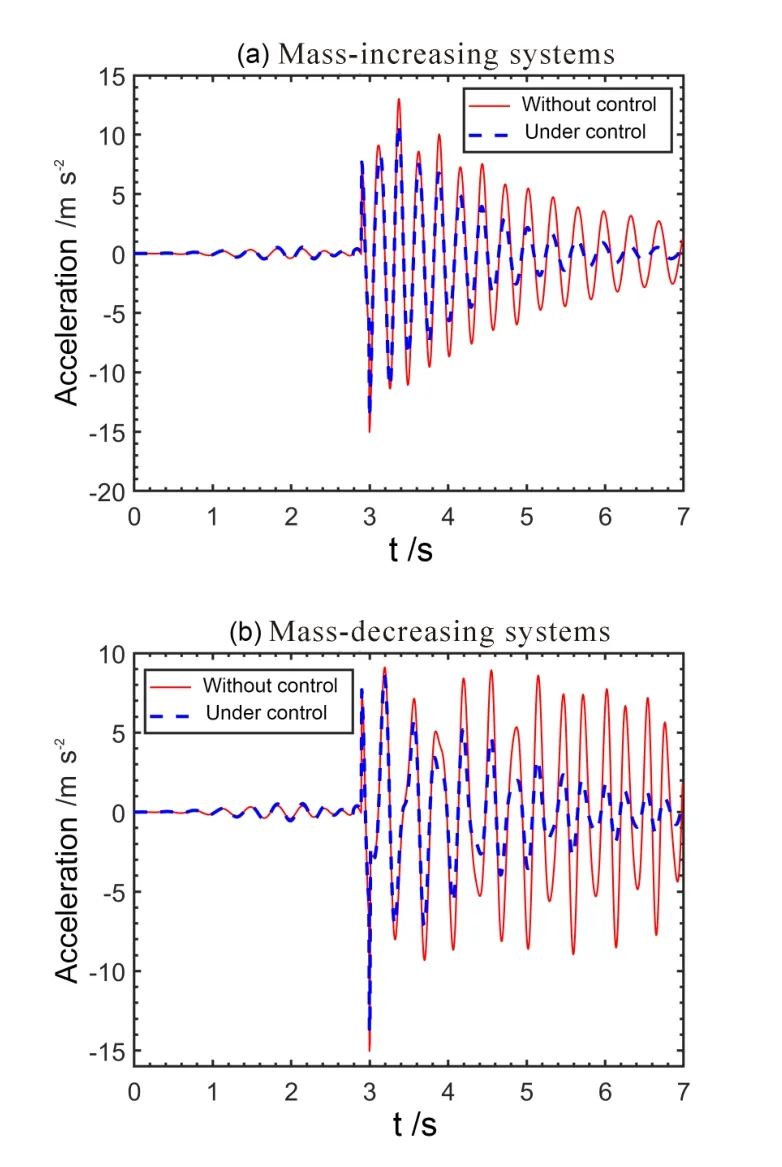
图10 负载质量变化时的控制效果Fig.10 Control results for the system with time varying payload

4 结论

本文主要开展了含变质量负载的双连杆机构的动力学分析及振动主动控制两个方面的工作.研究表明，负载的质量变化对系统的动力学响应有非常显著的影响，除了对频率的改变，还引起了一个附加的阻尼力效果.当负载质量增大时，引起一个正的阻尼力效果；当负载质量减小时，引起一个负的阻尼力效果.附加阻尼力对系统的动力学响应影响十分显著，当附加的负阻尼力的作用效果超过结构阻尼时，甚至会引起系统振动幅度的增大.在动力学分析的基础上，对含变质量负载的双连杆机构开展了主动控制研究，通过施加速度负反馈控制，有效地抑制系统的残余振动，从而提高了结构的运动稳定性和定位精度.后期的主要工作是变质量-双连杆结构的试验平台设计和先进控制算法在该类结构振动抑制中的使用，本文的工作可以为高精度机械臂结构的设计提供一定的参考.