LOCA下小型抑压式安全壳内流动与传热现象初步研究

陈耀峰,王升飞,*,方 圆,林盛盛

(1.华北电力大学 核科学与工程学院,北京102206;2.华北电力大学 非能动核能安全技术北京市重点实验室,北京102206)

抑压系统首先应用于BWR中,其快速降温降压、体积相对较小等特点,与小型堆的要求比较接近。因此,世界各国在小型堆概念设计中多采用抑压技术[1,2]。

Yutaka等人主要研究气体在沸水堆抑压水池中对于压力载荷的影响,在干井中分布较为均匀,蒸汽的流速以及空气的含量会影响干、湿井连通管的喘振机制,从而影响到连通管的压力载荷[3]。蒸汽进入抑压系统,与壁面发生传热冷凝,在抑压水池里发生直接接触冷凝,并且可能产生热分层等现象。Li等人通过30组试验研究蒸汽质量流量、整体水温和空气质量分数对于水池温度分布的影响,记录并分析凝结过程和温度分布的时间演变[4]。拉彭兰塔理工大学利用PPOOLEX台架,对热分层和混合进行试验研究,发现蒸汽的流量影响热分层的发生[5]。Song等人认为直接接触冷凝具有复杂性,轻水反应堆抑压水池中的热工水力现象很难预测[6]。Cai等人利用高速摄像机和粒子图像测速技术(PIV)观察气泡变化情况和运动规律,通过对气泡的行为分析,了解气体在湿井中的传热特性[7]。

国内研究工作主要集中在抑压水池,利用蒸汽或者其它高温气体,分析水池中射流及冷凝等行为[4,7]。事故后进入安全壳的高温气体包含不凝性气体,王坤等人[8]利用MELCOR程序,表明小型堆安全壳净容积较小,水蒸气含量较高,氧气含量较少,不会导致氢气爆炸。

上述研究多是针对BWR开展的,而国内关于抑压技术用于小型堆的研究较少。因此,有必要对小型抑压式安全壳内的流动与传热特性开展研究。由于整个抑压过程涉及相变、不凝气体、压力、温度、几何结构等多个因素,现象十分复杂。因此为更好地研究其机理,需要分阶段,逐一研究各因素的影响。第一阶段首先采用非相变工质空气开展研究;第二阶段采用蒸汽;第三阶段采用混合气体。本文是第一阶段的模拟研究,为后续的实验提供支持。

1 研究对象

1.1 几何模型

首先对抑压系统进行简化,将抑压系统简化为干井、湿井、连通管以及破口源,湿井由水空间和气空间组成,如图1所示。

干湿井隔板的中点为原点(0,0,0),以主视图向右为x轴,向上为y轴,俯视图向前为z轴正方向建立三维直角坐标系。

容器主体为干、湿井一体化抑压系统,破口源尺寸为25 mm,干湿井之间的连通管直径是80 mm,长度为850 mm,其余具体尺寸如图1所示。

1.2 网格划分

整个模型由209万个非结构化网格组成,网格模型图和质量图如图2所示。

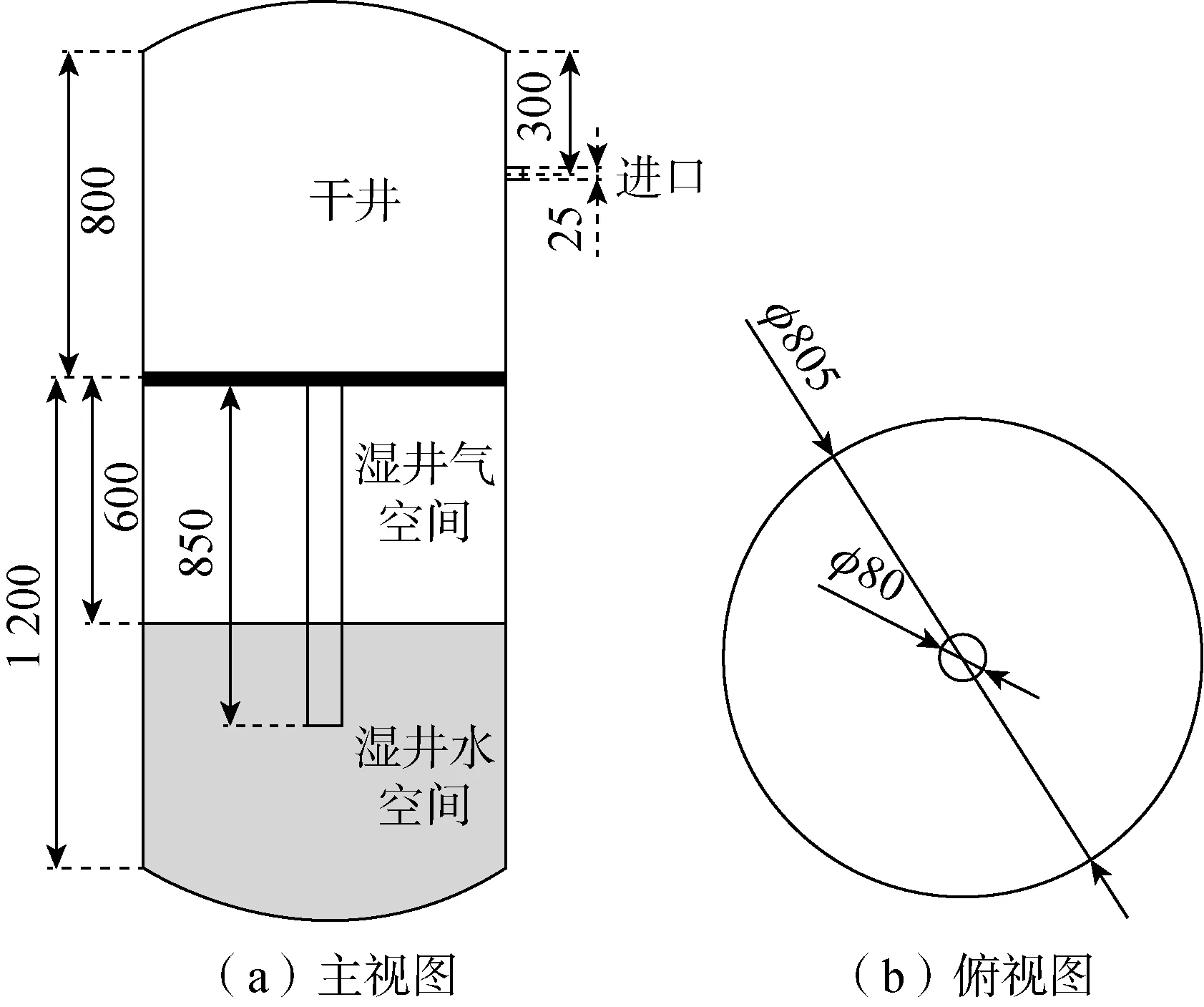
图1 抑压系统简化示意图Fig.1 Simplified schematic of the pressuresuppression system

图2 网格划分及质量Fig.2 Mesh and quality

网格总数分别选取138万、209万和308万,用以验证网格无关性。表1结果表明,209万网格在流场、温度上几乎不受网格数量影响,并且模拟计算速度较快,综合考虑,选取209万网格数量。

表1 网格无关性验证Table 1 Mesh independence verification

2 模型及参数设置

在文献[9]中,利用Fluent里VOF、标准k-ε湍流模型进行分析,并且模拟计算结果与实验结果吻合较好。本文研究的几何模型与之类似,采用干、湿井一体化设计,并且研究都涉及抑压系统温度及压力特性。因此选取PPOOLEX台架关于模型的一些相关设置。

2.1 VOF模型

2.1.1 体积分数方程

通过求解一个(或多个)相体积分数的连续性方程,可以实现相之间界面的跟踪。对于qth相,该方程的形式如下:

α、ρ和v——相q中的体积分数、密度和速度值;

Sαq——0相q体积分数的质量源,基值为0。

2.1.2 动量方程

在整个区域内求解一个动量方程,得到的速度场在各相之间共享。动量方程,通过物性ρ和μ,并且依赖于所有相的体积分数,具体表达式如下所示:

式中:μ——流体黏度;

F——表面张力;

ρ——相的密度;

g——重力加速度;

T——转置符号。

2.1.3 能量方程

各相之间的能量方程如下所示:

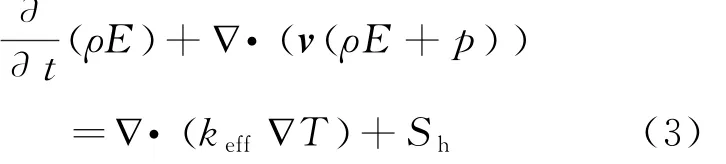
式中:E——能量;

Sh——源项;

T——温度;

p——压力;

keff——有效导热系数。

2.2 湍流模型

通过公式(4)～公式(5)的输运方程计算,可以得到湍流动能k和耗散率ε

式中:Gk——平均速度梯度下所产生的湍流动能;

Gb——由于浮力而产生的湍流动能;

YM——可压缩湍流中波动扩张对总耗散率的贡献;

C1ε、C2ε和C3ε——常数;

σk和σε——k和ε的普朗特数;

Sk和Sε——自定义的源项;

ρ、u和μ——密度、速度和流体黏度。

2.3 参数设置

模型选取多相流中经典的VOF模型。入口条件采用质量流率,初始容器内的压力为常压,温度为25℃,干井和湿井气空间为空气,空气为理想气体,其余物性参数采用Fluent默认值。抑压容器边界除入口外均密封,模拟时,壁面采取绝热处理,主要观察在干井和湿井中的变化情况。考虑进口速度和管径大小,采用标准k～ε模型进行计算,近壁面选取可伸缩壁面函数(Scalable Wall Functions)。

3 模拟结果分析

由于模拟是为后续试验做支持,因此工况的选取由实验台架的参数范围及待研究的关键因素(温度、流量)共同决定。计算工况如表2所示。

表2 计算工况表Table 2 Calculation conditions

3.1 流动过程分析

图3 从左到右,依次为工况1在0.4 s,0.8 s,1.2 s时刻干、湿井内的温度分布。由图可知,空气从破口喷出,以一定速度撞击到干井壁面,对壁面造成热冲击,有可能导致热疲劳损伤。

图3 工况1不同时刻温度分布图Fig.3 The temperature distribution at different moments for Case 1

空气继续沿着壁面向周围流动,干井上、下空间各形成1个环流。下半空间的环流在连通管附近,一分为二,部分空气沿管道向下进入湿井,其余部分空气继续加热干井的下半空间。之后,进入连通管的气体在压差作用下进入湿井水空间,加热过冷水并从连通管底部溢出。

图4 为工况1对应时刻干、湿井内的体积分数。由图可以看出,热空气以气泡的形式从连通管管口冒出,然后在浮升力作用下,从湿井水空间溢出,并导致液面产生一定幅度波动。

图4 工况1体积分数图Fig.4 The volume fraction diagram for Case 1

图5 为工况1压力在0.4 s,1.2 s时刻分布。由于水的静压力和空气压力的影响,压力分布呈层状结构。随着时间推移,气体质量增加,干井压力升高,并且在连通管出口附近产生压力波动,对连通管管壁产生一定压力载荷。

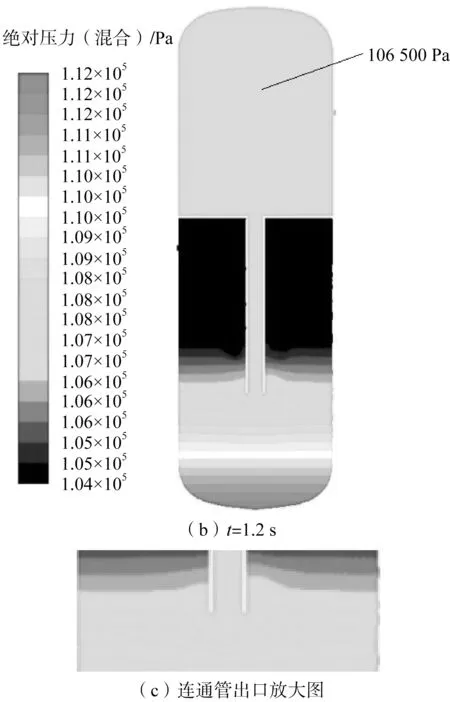
图5 工况1压力分布图Fig.5 The pressure distribution diagram for Case 1

3.2 进口质量流速影响

图6 为工况2云图分布。通过与工况1在1.2 s时温度分布对比,发现干井内整体温度升高,并且湿井内气空间的温度产生变化。说明热空气在湿井水空间冷却后溢出水面,继续加热湿井气空间。

图6 工况2云图分布Fig.6 The cloud diagram distribution for Case 2

对于体积分数分布,由于流速增大,气体更快地进入湿井,水面的波动更加剧烈。而且,流速增加使抑压容器内压力整体升高,干井和连通管出口压力变化明显。

3.3 进口温度影响

图7 为工况4云图分布,将工况4与工况2进行比较分析。由于进口温度增加,1.2 s时,工况4干井内温度更高,并且加热速度更快,换热更强,湿井内温度分布与工况2基本一致,但连通管出口和水空间液面温度因为气泡温度的不同而不同;对于体积分数,变化都比较剧烈,但气泡分布形式有所差异;压力大小和分布大致相同。

图7 工况4云图分布Fig.7 The cloud diagram distribution for Case 4

3.4 流速和温度对压力具体影响

3.4.1 连通管出口压力分析

空气进入容器1.2 s时,在连通管出口附近,压力产生波动,其它位置变化平稳。由图8(a)可知,流速越大,水平方向整体压力升高,管口附近压力振荡加剧。对于图8(b)中工况2和工况4,在1.2 s时刻,当破口温度升高,连通管出口中心水平线方向压力整体升高,并且在连通管出口附近压力振荡明显;对于工况4和工况5,在管口处附近,温度变化导致振荡幅度加大。

图8 出口水平面方向压力变化Fig.8 The pressure change in the direction of the outlet horizontal plane

3.4.2 干湿井中心压力分析

连通管出口平面中心点的坐标为(0,-850,0)。在图9(a)中,由于水的静压力影响,湿井水空间的压力要大于湿井气空间的压力和干井的压力。连通管管口压力变化与图8一致,存在压力振荡,流速越大,振荡越明显。通过图9对比发现,湿井底部到干井顶部的压力差均随着容器进口流速和温度增大而改变。相对于入口温度的增加,流速的增加对于湿井底部与干井顶部压力差的影响更显著。

图9 湿井底部到干井顶部的中心线方向压力变化Fig.9 The pressure change in the centerline direction from the bottom of the wet well to the top of the dry well

4 结论

利用Fluent软件,模拟以空气为工质的LOCA下抑压系统内流动与传热变化,分析其演变过程及各因素的影响,得到以下结论:

(1)热空气以喷射的方式进入干井,对壁面产生一定的热冲击。随后形成上、下2个环流加热干井,同时使热空气得到初步冷却。随后,热空气通过连通管进入湿井水空间进行对流传热,气体温度进一步降低。最后,气泡从水空间溢出,对水面造成扰动,导致压力波动,有可能影响容器的完整性。而且,溢出的气体持续加热湿井气空间,使其压力逐渐增大。

(2)由于射流和气泡的影响,在连通管出口附近产生压力振荡,随工质流速和温度增大而加强;湿井底部与干井顶部的压力差,同样受破口流速和温度影响,并且流速对于该压力差的影响更显著。