ADS 次临界堆堆芯功率控制策略研究
刘依诺,胡 杨,李楚豪,梁乐华,惠天宇,曾文杰,2,*
(1.南华大学 核科学技术学院,湖南 衡阳 421001;2.中国原子能科学研究院,北京 102413)
加速器驱动次临界反应堆(Accelerator Driven subcritical System,ADS)可以满足发电、增殖和嬗变等多种需求[1-3]。在产生能量发电的同时,还能嬗变核废物,实现堆内核废料最少化。要使其较好地完成嬗变或发电,都要求ADS系统能以稳定的功率运行[4]。ADS次临界堆的功率控制与临界堆有本质的不同,临界堆大多以控制棒为控制手段调节功率,而ADS次临界堆的功率控制以移动控制棒引入反应性和质子加速器束流轰击散裂靶产生外中子源来实现。
选取文献[5,6]中热功率为10 MW的小型次临界反应堆系统为研究对象,针对ADS堆芯功率控制系统的特殊性,提出一种“切换受控对象”的堆芯功率控制方案,将控制棒反应性和外中子源相对强度同时设为受控对象,根据不同的堆芯相对功率偏差大小,切换受控对象来实现堆芯功率控制。通过建立ADS次临界堆芯模型,基于Matlab/Simulink仿真平台搭建ADS堆芯功率控制系统,分别开展引入阶跃反应性、阶跃外中子源相对强度的扰动仿真分析。
1 ADS次临界堆堆芯模型
2011年,中国科学院启动了“未来先进核裂变能ADS嬗变系统”战略优先研究计划[3],ADS次临界堆堆芯功率的控制除了受到棒控系统的影响之外,加速器外中子源强度及与之对应的次临界深度对功率也有很强的制约性[5]。本文依据文献[5,6]提供的研究对象参数,建立堆芯传递函数模型。
1.1 堆芯非线性模型
忽略碘氙等核反应堆毒物效应,建立适用于短时间内堆芯动态仿真的非线性模型。
(1)点堆动力学模型
具有六组缓发中子的点堆中子动力学模型[5]:


式中:t——时刻;
Pr——相对功率;
Cir——第i组缓发中子先驱核相对密度(i=1,2,…,6);
q0——外中子源初始强度;
qr——外中子源相对强度;
P0——堆芯初始功率;
ρ——引入堆芯的总反应性/×10-5;
βi——第i组缓发中子份额;
β——缓发中子总份额;
λi——第i组 缓 发 中 子 先 驱 核 衰 减常数/s-1;
l——堆内瞬发中子平均寿命/s。
(2)堆芯热工模型
根据能量守恒原理,堆芯燃料换热方程及冷却剂温度方程如下[5]:

式中:P——堆芯功率;
T——温度/℃;
M——质量/kg;
Uf,lb——燃料与冷却剂间总的换热系数/W·K-1;
C——热容量/kJ·kg-1·K-1;
Glb——冷却剂质量流量/kg·s-1。
下标:f、lb、i和o分别表示燃料、铅铋合金、堆芯进口段和堆芯出口段。
式(3)、式(4)中:

(3)反应性反馈模型
公式(1)中反应性ρ(t)可以表示为[6]:

式中:ρd——调节棒引入的反应性价值;
αf,αc——燃料的多普勒系数和慢化剂温度系数;
Tf0——燃料平均温度稳态值/K;
Tlb0——堆芯冷却剂平均温度稳态值/K。
由式(1)、式(2)、式(3)、式(4)、式
(6)构成堆芯非线性模型。
1.2 ADS次临界堆堆芯状态空间模型
利用微小扰动方法[7,8]对堆芯非线性模型进行线性化处理,建立ADS堆芯状态空间模型,



2 ADS堆芯功率控制设计与仿真
2.1 ADS堆芯功率控制原理
ADS堆芯功率采用控制棒和加速器相互协调的方式控制[5],利用控制棒调节堆芯反应性大小,利用质子加速器调节堆芯外中子源相对强度,由此建立双输入(控制棒反应性和外中子源相对强度)双输出(堆芯相对功率和冷却剂平均温度)控制系统,现拟定两种ADS堆芯功率控制方案。
方案一控制原理如图1所示,将控制棒反应性设为受控对象,采用PID控制器[9,10],建立堆芯功率控制系统。
方案二控制原理如图2所示,将控制棒反应性和外中子源相对强度同时设为受控对象,当堆芯功率变化较大时,需要引入外中子源强度实现功率控制;当堆芯功率变化较小时,可利用控制棒调节反应性实现功率微调。因此,当输出的堆芯相对功率偏差大于等于0.01时,作用在质子加速器上的PID控制器工作;当输出的相对功率偏差小于0.01时,作用在控制棒上的PID控制器工作,由此建立堆芯功率控制系统。
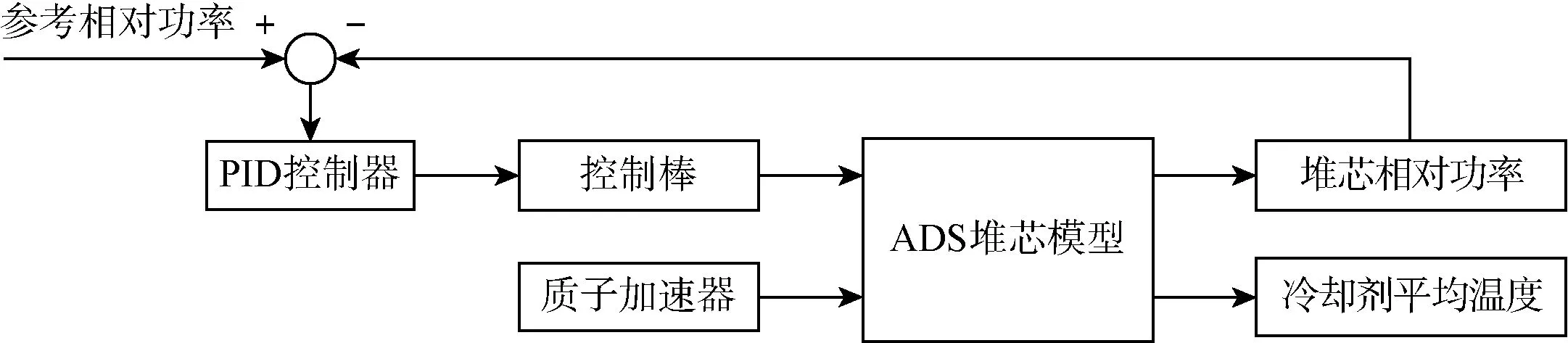
图1 方案一的ADS堆芯功率控制系统原理图Fig.1 Schematic of the ADS core power control system in Scheme 1

图2 方案二的ADS堆芯功率控制系统原理图Fig.2 Schematic of the ADS core power control system in Scheme 2
2.2 仿真分析
以文献[5,6]中的ADS堆芯为对象,依据ADS堆芯功率控制原理(如图1、图2所示),基于MATLAB/Simulink仿真平台搭建ADS堆芯功率控制系统,开展动态仿真研究。
2.2.1 阶跃引入外中子源相对强度
在初始满功率水平下,堆芯外中子源相对强度阶跃扰动0.05、0.1,堆芯相对功率偏差响应结果如图3所示,堆芯冷却剂平均温度偏差响应结果如图4所示。堆芯相对功率偏差响应的主要数据如表1所示。由图3、图4可知,无论阶跃引入的外中子源相对强度是0.05还是0.1,堆芯相对功率偏差都在15 s内趋于零,堆芯冷却剂平均温度偏差从初始时刻迅速增大后减小,直至150 s趋于零。从表1中可以看出,在外中子源相对强度阶跃0.05下,方案一中堆芯相对功率偏差在1.5 s时达到最大幅值0.023 5,方案二中堆芯相对功率偏差在1 s时达到最大幅值0.018 5。在外中子源相对强度阶跃0.1下,方案一中堆芯相对功率偏差在1.6 s时达到最大幅值0.047 5,方案二中堆芯相对功率偏差在1 s时达到最大幅值0.035。方案二相较于方案一,系统响应的上冲幅度和超调量都显著减小,由此可见,在外中子源相对强度扰动下,对于ADS堆芯功率控制,方案二的效果更佳。


图3 堆芯相对功率偏差响应Fig.3 The core relative power deviation response

图4 堆芯冷却剂平均温度偏差响应Fig.4 The core coolant mean temperaturedeviation response

表1 堆芯相对功率偏差仿真结果数据表Table 1 Data sheet of the core relative power deviation simulation results
2.2.2 阶跃引入反应性
在初始满功率水平下,引入80×10-5、100×10-5的阶跃反应性,堆芯相对功率偏差结果如图5所示,堆芯冷却剂平均温度偏差结果如图6所示。堆芯相对功率偏差响应的主要数据如表2所示。由图5、图6可知,无论阶跃引入反应性是80×10-5还是100×10-5,堆芯相对功率偏差都在15 s内趋于零,堆芯冷却剂平均温度偏差从初始时刻迅速增大后减小,直至150 s趋于零。如表2所示,在反应性阶跃80×10-5下,方案一中堆芯相对功率偏差在1.7 s时达到最大幅值0.018 5,方案二中堆芯相对功率偏差在1 s时达到最大幅值0.014 1。在反应性阶跃100×10-5下,方案一中堆芯相对功率偏差在1.7 s时达到最大幅值0.023 1,方案二中堆芯相对功率偏差在1 s时达到最大幅值0.017 2。方案二相较于方案一,系统响应的上冲幅度和超调量都显著减小,由此可见,在反应性扰动下,对于ADS堆芯功率控制,方案二的效果更佳。

图5 堆芯相对功率偏差响应Fig.5 The core relative power deviation response

图5 堆芯相对功率偏差响应(续)Fig.5 The core relative power deviation response

图6 堆芯冷却剂平均温度偏差响应Fig.6 The core coolant mean temperature deviation response

表2 堆芯相对功率偏差仿真结果数据表Table 2 Data sheet of the core relative power deviation simulation results
3 结论
为研究ADS次临界堆堆芯功率控制问题,考虑到ADS次临界堆功率调节方式的特殊性,设计了两种堆芯功率控制方案。基于Matlab/Simulink平台建立ADS双输入双输出堆芯功率控制系统,开展切换受控对象和仅以控制棒为受控对象的两种控制方案仿真。仿真结果表明,在阶跃引入外中子源相对强度和阶跃引入反应性的情况下,两种方案均可实现堆芯功率控制,且采用切换受控对象的方案,可使堆芯相对功率和堆芯冷却剂平均温度的超调量显著减小,迅速回归稳定,控制效果更佳。

