基于模拟实验的低等级公路车辆过弯风险预测模型

柳本民，廖岩枫，涂辉招，管星宇

（同济大学道路与交通工程教育部重点实验室，上海201800）

道路线形是影响车辆行驶安全的重要因素之一，而圆曲线作为道路线形的主要组成部分，具有较大的风险性，尤其是低等级公路小半径曲线路段，更是驶离车道、护栏碰撞、翻车等事故的高发区域。国外相关研究表明，在其他条件相同的情况下，弯道发生事故的概率比直线路段高3～4倍［1］，因此，对车辆过弯风险的研究具有较大的现实意义。

车速是衡量车辆过弯风险的一个重要指标，目前国内外对于车辆过弯的相关研究大部分是基于车速展开的。许多过弯车速的相关研究主要是为了道路线形优化服务的，有些研究者通过对过弯车速的预测来评价不同道路单元设计的连续性［2-3］，也有一些研究致力于探寻过弯行驶车速与圆曲线设计参数之间的规律，其中被重点关注到的设计参数包括设计车速及圆曲线半径［4-6］。随着计算机技术的发展，近年来，过弯车速的相关研究越来越与自动驾驶辅助系统相关联，Serna 等人通过GPS 数据构建了动态车速自适应系统，该系统在自动驾驶系统中有较好的应用［7］，Zhang等人通过不同的驾驶风格构建了弯道车速预测模型，并将该模型应用到了自适应巡航系统（ACC）中［8］。

除了车速以外，车辆过弯轨迹的相关研究也是过弯风险的研究热点之一，横向偏移、方向盘转角（转速）、道路附着系数等与过弯轨迹相关性较大的参数常常是研究重点。彭其渊等通过曲中速度增量及轨迹半径的增量来描述车辆过弯时的切弯行为，从而得到道路半径、方向盘转角等对切弯行为的影响规律［9］，Hallmark 等通过对道路、周边环境、驾驶人特性因素的分析，基于逻辑回归构建了车道偏离概率模型［10］。王恒等基于不同的圆曲线半径、超高值及路面附着系数值搭建了驾驶模拟实验场景并进行了数据分析，结果表明附着系数对载重汽车弯道侧滑影响显著［11］。

而目前相关的车辆过弯风险模型主要为车速预测模型，车速预测模型主要是从车速在弯道中的变化规律出发，对平均车速或不同道路单元的车速进行预测［12-13］，有时候还会考虑不同驾驶风格或驾驶模式的影响［14］。相比于车速，轨迹的变化更为无序性，因此，弯道轨迹预测模型的研究较少，主要是从横向偏移的规律性出发的［10］。除此以外，还有基于道路设计参数等客观因素进行的弯道事故率计算模型［15］，该类模型对道路设计具有较大的指导意义，但并未考虑不同驾驶员个体的差异性。

因此，在车辆过弯风险的相关研究中，车速与轨迹是研究的重点，二者主要对应车辆在行驶过程中的纵向风险和横向风险，纵向风险即可以用平行于车辆行驶方向的向量来表征的风险，如与车速、加速度相关的超速、刹车失灵等风险；横向风险即可以用垂直于车辆行驶方向的向量来表征的风险，如与横向偏移、方向盘操作相关的急转弯、侧滑等风险。除了与车辆行驶相关的参数外，环境参数也是必不可少的一环，包括道路半径、路面附着系数、设计车速等。可以通过综合考虑环境行驶参数及环境参数的影响，针对不同的驾驶员个体，对车辆过弯时可能遇到的风险进行分类及识别，从而达到风险防控的目的。

1 驾驶模拟实验

由于小半径曲线路段，尤其是道路附着系数较低的工况下，行车具有一定的危险性，因此，采用驾驶模拟实验的方式进行数据采集，主要依托仪器为同济大学8 自由度驾驶模拟器，根据不同的环境参数设置了不同的驾驶模拟实验场景，并对各个场景下采集到的行驶参数进行进一步的分析与提取。

1.1 实验场景设计

实验场景为四级公路，全长约6km，双向两车道。根据冰、雪、雨、晴四种天气场景设置4 个子路段，每个子路段线型相同，但道路摩阻系数不同。为减小两相邻圆曲线之间驾驶行为的影响，直线长度与缓和曲线长度应保证足够的行驶时间，以供驾驶员调整车速及轨迹，同时直线长度取值过大又会显著增加路段长度，导致模拟驾驶负荷的增高，因此综合考虑以上两点因素，直线长度的确定原则为：车辆在直线与两侧缓和曲线上的行驶时间之和稍许超过10s，以保证驾驶人有充足时间调整车速与行车路线。各子路段超高加宽如表1 所示。图1 为子路段的平曲线要素设置，其中，R为圆曲线半径；Ls1与Ls2为两侧缓和曲线长度；L为平曲线总长度；T1、T2为两侧切线长度；E为外距。

表1 子路段弯道设计参数Tab.1 The linear parameters of the sub-section road

实验为单车实验，根据相关研究，各路面附着系数的取值范围大致如下：干燥路面0.65～0.75，湿润路面0.35～0.55，积雪、轻度压实雪路面0.25～0.35，冰膜0.15～0.30［16］。因此，取结冰路面场景的道路摩阻系数为0.2，积雪路面场景的道路摩阻系数为0.3，雨天湿滑路面场景的道路摩阻系数为0.5，正常干燥路面场景的道路摩阻系数为0.8，各子路段线型相同，随机地以首尾相连，整体平面线形如图2所示。在实际情况中，低等级公路的纵坡通常较大，平纵线型组合复杂多变，本研究主要针对弯道驾驶风险，为了控制变量，减少纵坡对实验的影响，竖曲线纵坡均为0。

1.2 数据采集及筛选

实验共采集了12 名专业司机的驾驶数据。采集的数据类别可分为四类：①是驾驶员操作数据，包括方向盘扭矩、方向盘力反馈、方向盘转角、方向盘受力、刹车踏板受力、油门踏板受力；②是车辆的力学反馈，包括轮胎刹车力、三轴加速度；③是车辆的运动学参数，包括车辆的三向速度、行驶里程、车辆坐标、及横向偏移；④是环境参数，包括道路附着系数、道路线形相关参数。前三类数据又可进一步概括为车辆的横向数据及纵向数据，横向数据包括方向盘相关数据及横向偏移，纵向数据包括车辆的速度与加速度相关数据。

为了较为全面地反映过弯时的横向风险与纵向风险，提取了速度标准差、横向偏移量最大值、横向偏移量标准差、切向加速度标准差、切向加速度均值、横向加速度最大值、方向盘角速度均值、方向盘角速度标准差共8个行驶统计参数作为主要的研究对象。考虑车辆在进入直缓点后，横向受力即开始发生较为明显的变化，选取直缓点至缓直点间的驾驶行为数据作为弯道数据进行分析。剔除无效数据后，共得到166组有效数据，其中包含了不同的半径及道路附着系数组合情况，具体过程如图3所示。

为了便于进一步分析，通过主成分分析（PCA）对8个统计参数进行降维处理。在主成分分析中一般满足n＜p，其中n为最后筛选出的成分个数，p为原始的成分个数。要求所取的n个主成分的方差累计贡献率∂最好超过80%，累计贡献率代表的是对原始特征信息的反映程度，计算∂如式1 所示，λi为第i个成分的方差贡献率。

图1 子路段线形Fig.1 The aligment of road sections

图2 实验道路整体平面线形Fig.2 The aligment of the whole experment road

方差贡献率的计算结果如表2所示。

由表2 可知，方差贡献率最大的三个主成分累积贡献率接近80%，因此可提取三个主成分，各主成分的系数计算结果如表3的成分矩阵所示。

记第i个主成分为Xi，lij为第i个主成分中第j个原始成分对应的系数，则Xi的表达式如下：

定义行车风险综合评价指数F如下：

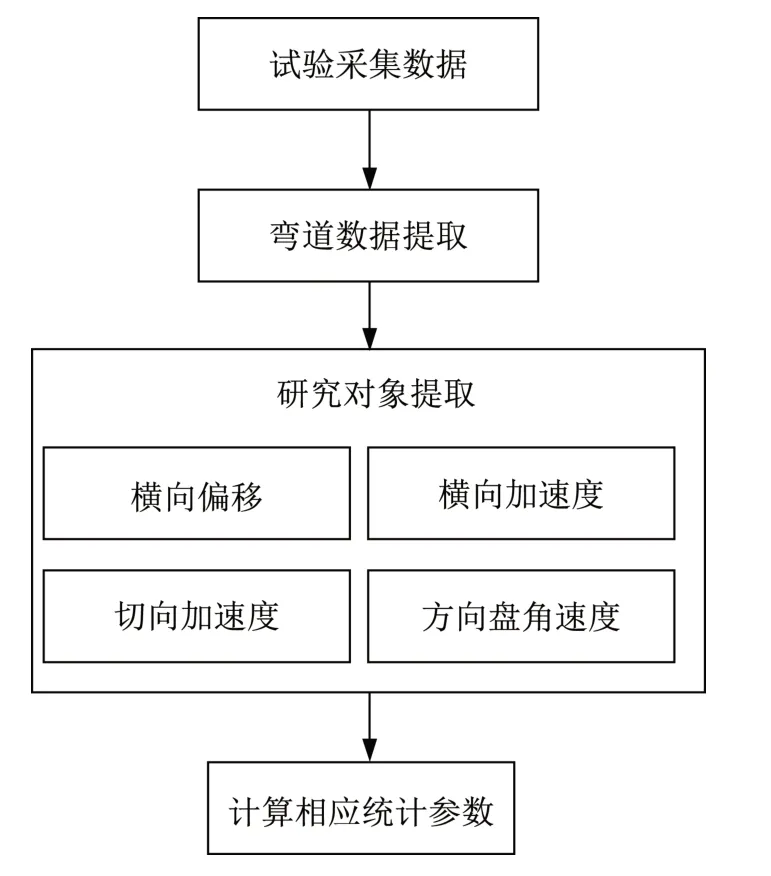
图3 数据处理过程Fig.3 The processing of data analysis

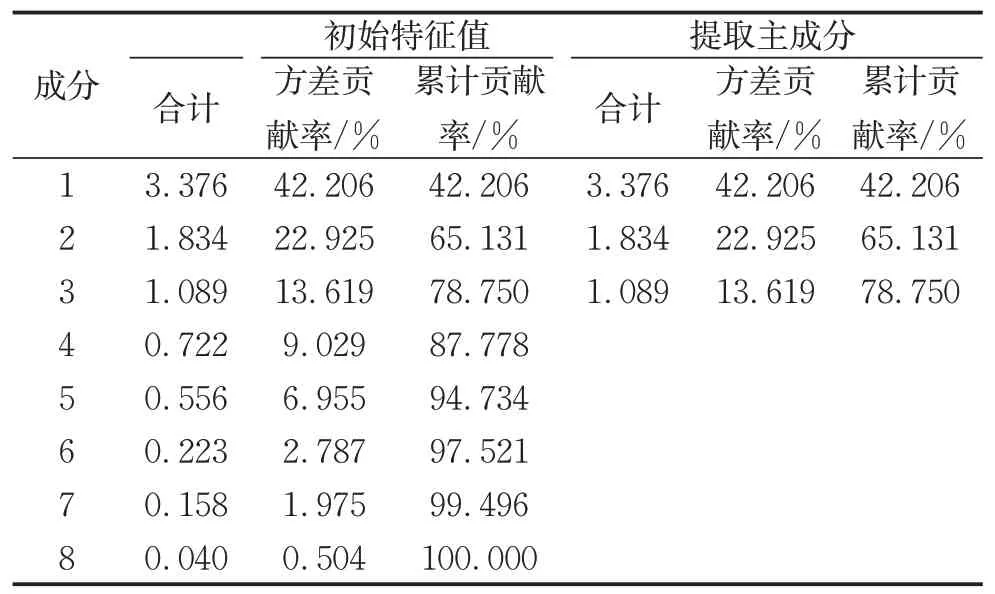
表2 主成分分析方差贡献率Tab.2 The variance contribution rate (PCA)

表3 成分矩阵Tab.3 Matrix of factors

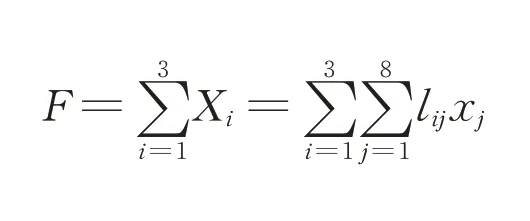
第j个原始成分的系数绝对值之和记为Lj，则

可知，原始成分对应的L越大，则该原始成分对综合风险评价指数F的影响越大，因此，降维可进一步简化为寻找使L值最大的原始成分。根据计算，L值最大的三个原始成分为：速度标准差、切向加速度标准差及方向盘转速均值（L值分别为1.435、1.412及1.365），即在原始的8 个统计参数中，速度标准差、切向加速度标准差及方向盘转速对行车风险的影响最大，可将这三个变量作为主成分进行后续分析。

2 车辆过弯风险分类

由上文可知，提取的三个主成分为速度标准差、切向加速度标准差及方向盘转速均值，这三个主成分能较好地反映车辆过弯时的速度、轨迹规律，可进一步用于车辆过弯风险的分类中。运用k均值聚类的方法，以三个主成分为三个维度进行分类，可得到低等级公路车辆过弯时可能出现的风险类别及相应特征。

2.1 k值的选取

所谓k均值聚类，即给定一个样本容量为n的集合X和类别个数k，k均值聚类法的任务是搜索对集合X的一个最优k划分，即分成k个组，使组内离差平方和达到最小值，组内离差平方和是指组内样本到组均值的累计距离平方。

在聚类前，需选定k值，即类别数，可通过计算轮廓系数，寻求使各类别区分度最大的k值。每个样本点都可计算其轮廓系数，第i个样本点的轮廓系数计算式如下：

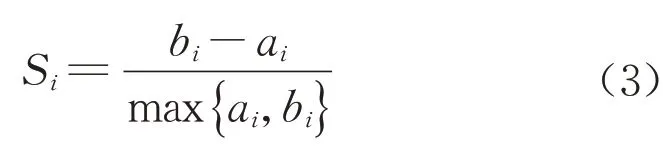
式中：ai为组内不相似度，即第i个点与同类的其他点之间的平均距离；bi为组间不相似度，即第i个点与不同类的类内各点之间的平均距离的最小值。而整个聚类结果的轮廓系数S为Si的均值，即

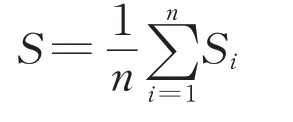
计算当k=2～6时的轮廓系数，结果见表4。

由表4 可知，当k=2 时，轮廓系数最大，聚类效果最好，但此时类别较为单一，从实际意义出发，并不能较好地反映车辆过弯时的风险规律。通过尝试，发现当k=4时，各类别的速度、转角变化规律特征最为明显，因此，最终确定的k值为4。

表4 轮廓系数Tab.4 The silhouette coefficients

2.2 k均值聚类过程及聚类结果

k均值聚类分析的质心可以理解为每一个组的中心，即聚类中心，判别某个数据点归属于哪个组时，只需考察该点与各组质心的相似度，并将该点归入相似度最高的组。k均值聚类算法包含了多种类型的相似度度量方式，选取欧式距离进行相似度度量，则目标函数，即组内离差平方和J如下：

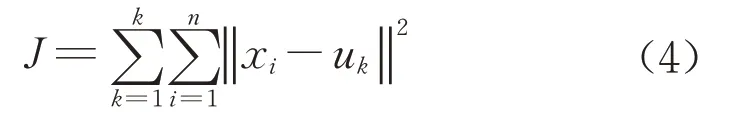
式中：xi为第i个数据点；uk为第k个组的聚类中心。聚类的结果应使J尽可能小。

选取166组有效数据进行k均值聚类，其中包含了各种5种道路半径及4种道路附着系数的情况，聚类过程不单独考虑各线形及道路附着系数的具体情况，仅从车辆的行驶状态考虑车辆过弯的风险，即以速度标准差、切向加速度标准差、方向盘转速均值作为三个维度，最终聚类结果如图4所示。各类别的聚类中心如表5所示。

图4 过弯风险聚类结果Fig.4 The result of risk clustering

表5 聚类中心Tab.5 The clustering center

由此，可以归纳出不同风险类别的相应特征，如表6所示。

表6 风险说明Tab.6 Risk instructions

不同半径下的风险分布如图5所示。根据图5，Ⅰ类风险在半径为35m的弯道上，发生的频率最大，甚至超过了半径为15m 的弯道，可以解释为驾驶员在面对极限最小半径时，更为谨慎，能将风险控制在一定范围内，反而是半径稍大时，驾驶员放松了对风险的预判，造成Ⅰ类风险急剧上升。Ⅱ、Ⅲ类风险在各弯道上分布得较为平均，不难看出，半径为15m的弯道较易发生急转弯，而半径为270m的弯道较易发生急刹车，且综合道路附着系数可知，后者主要发生在道路附着系数较小的时候。

根据以上分析可提出如下工程建议：

（1）应尽量避免使用小半径曲线，条件较为苛刻时，也需做好视线诱导、警示标语等措施，尤其是半径为35m左右的弯道路段。

（2）冰雪区域的低等级公路路段，应做好防雪防滑措施，尤其在半径较大的路段，还应通过警示标语等形式提醒驾驶员谨慎驾驶，注意行车安全。

图5 风险分布Fig.5 The distribution of risk

3 车辆过弯风险预测模型

过弯风险预测主要需要实现以下过程：通过某个时段内的行驶数据，来预测车辆过弯时可能遇到哪一类风险。此过程可以运用有监督的机器学习方法来实现，传统的机器学习方法如神经网络、马尔可夫链等，在此处均不太适用，主要是由于数据量过小且测试集的输出变量过于规整。由于数据量的问题难以解决，所以考虑从选择更适用于本文数据结构的模型的角度来解决问题。k均值聚类所获得的风险类别主要是基于欧式距离进行划分的，因此，可以选择同样是基于“距离”的概念来进行多分类的Fisher模型来进行过弯风险的预测。

3.1 Fisher模型简介

在交通运输领域，Fisher 常被用于驾驶模式的判别，如金辉等就运用了改进Fisher的方法，对不同驾驶风格的起步工况进行了判别［17］，其研究思路对本文也有较大的借鉴意义。

Fisher 的基本思想是通过高维映射到低维，寻求一条直线，使投影到其上的各类数据点之间的间隔最大。其分类逻辑是使类与类之间的距离最大化，和k均值聚类的逻辑类似，但Fisher 是有监督学习，因此可以实现识别的功能。其核心公式如下：

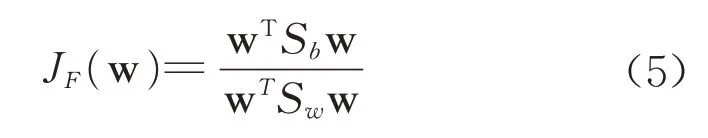
式中：JF是Fisher判别函数；Sw是类内离散度；Sb是类间离散度；w为表征一条直线的向量。使JF最大的w即为所求空间向量，将其定义为w*，即w*能使投影到其上的数据点间隔最大，因此

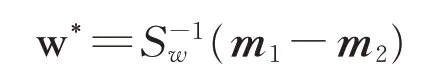
式中：m1与m2为两类样本的平均值向量。以上过程为二分类过程，若要实现多分类，则重复上述过程即可。

3.2 基于Fisher的过弯风险预测模型

传统的Fisher 可以实现模式的判别，但并不能进行预测。然而，对整段弯道的行驶数据进行风险识别，并不能有效防控风险，且实际意义并不大，必须尽可能在风险发生前实现风险的预测，才能及时对驾驶员发出预警，从而实现风险的防控。因此，需要调整Fisher 模型的测试集与训练集构成，可将整段弯道的行驶统计参数作为训练集，而测试集则选取车辆从直缓点开始驶入弯道的t时刻内的行驶参数。

从实际意义出发，t越小则越有助于风险的及时预警，但理论上，t过小则会造成训练集与测试集相关性过小的问题。综合考虑实际意义以及理论可行性，t值取1/4的过弯总时长。

对t时刻内的速度标准差、切向加速度标准差及方向盘转速均值进行计算，分别记为x1*，x2*，x3*，而整段圆曲线的的相应统计参数记为x1，x2，x3，计算两组数据的皮尔森相关性，结果如表7所示。

表7 测试集与训练集数据相关性Tab.7 Correlation between test set and training set data

因此，t时刻内的行驶统计参数与总时长内行驶统计参数相关性较大，可以将其视为同一种类的数据，分别作为测试集与训练集进行Fisher建模，具体建模流程如图6所示。

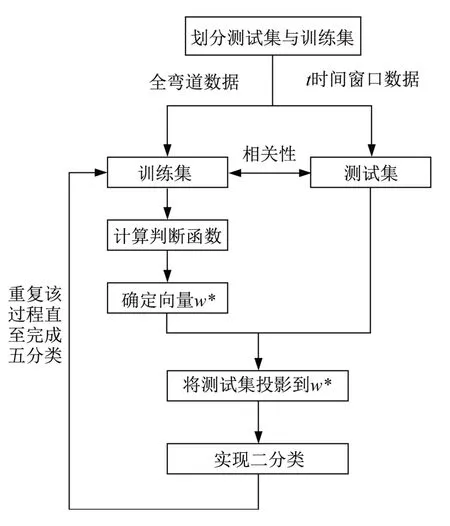
图6 Fisher建模流程Fig.6 The processing of Fisher modeling

预测结果如表8 所示，其中正确预测个数为预测结果与原始结果一致的个数，其总数应不大于原始数据点个数。

将数据点进行编号，原始值与预测结果之间的误差如图7所示，其中，误差为负则说明预测的风险等级高于原始值，预测的结果是偏于安全的，误差为正则说明预测的风险等级低于原始值，即未能识别出潜在的风险。结合表8 可知，预测模型对于最为危险的Ⅰ类风险的预测精度最高，Ⅱ、Ⅲ类风险较易相互混淆，结果整体是偏于安全的。

表8 Fisher预测结果Tab.8 The predicted results by Fisher model

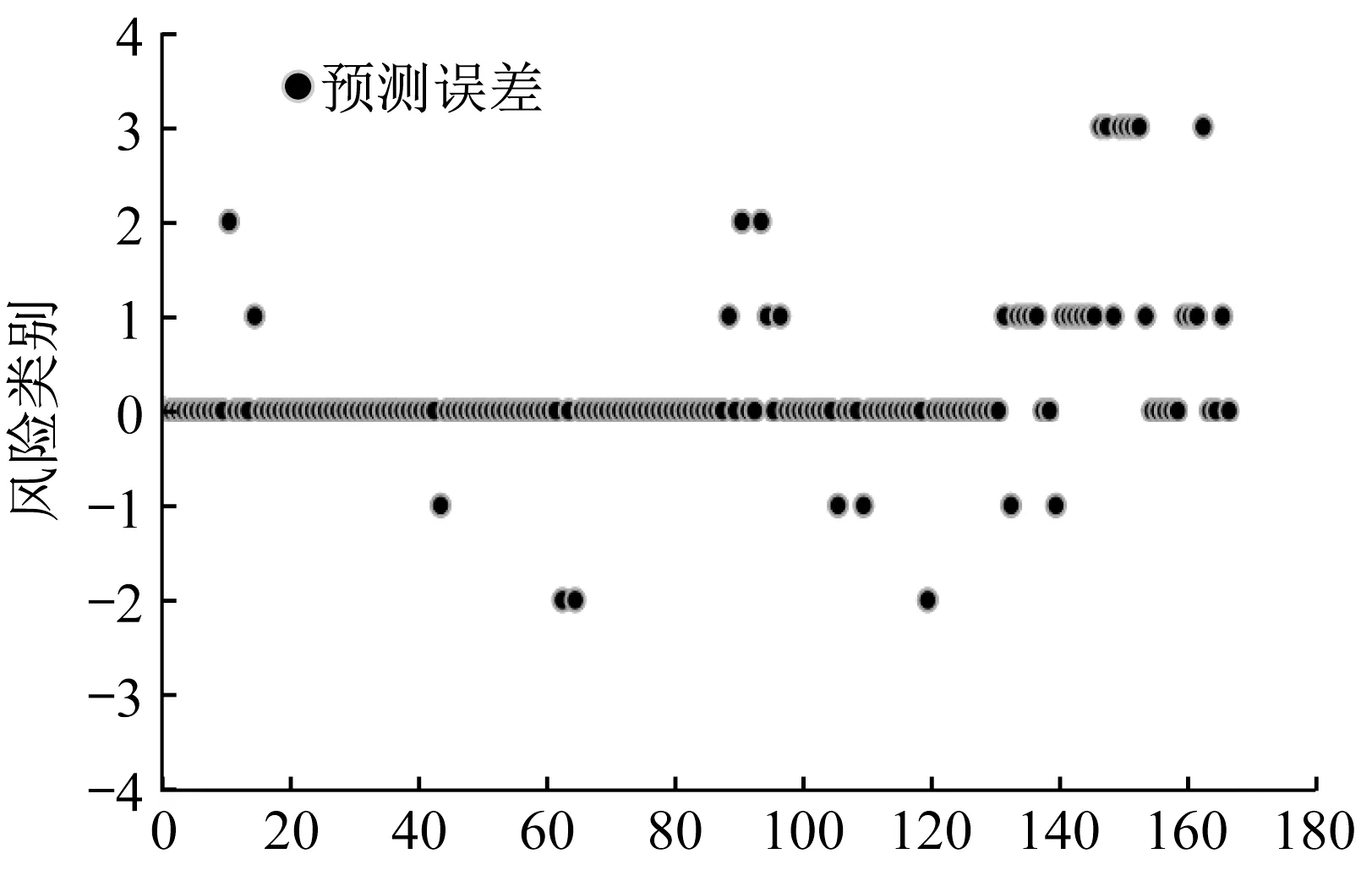
图7 预测误差Fig.7 Prediction error

整体的预测精度为76.5%，预测效果较好。根据表8及图2可知，风险最大的Ⅰ级风险的预测准确率最高，Ⅳ级风险次之，而Ⅱ级及Ⅲ级风险较易互相混淆。误差总体向高风险倾斜，即大多数误报的案例为低风险误报为高风险，在实际驾驶过程中，有助于提高驾驶员的风险意识，具有较大的应用价值。

4 结论及展望

通过模拟驾驶的实验数据，对低等级公路车辆过弯存在的风险进行了分类识别，进一步明确了过弯风险产生的原因及机理，并通过机器学习的方法，构建了车辆过弯风险预测模型，为车辆过弯风险的可防可控创造了最基本的数学依据。主要研究成果如下：

（1）设计并进行了低等级公路车辆过弯的单车实验，对驾驶数据进行了统计分析并筛选出了速度标准差、切向加速度标准差及方向盘转速均值作为重点研究对象。

（2）进行三维k均值聚类，得到了车辆过弯时的四类典型风险情形：刹车油门方向盘均失控、急转弯、急刹车以及车辆总体把控良好。

（3）基于聚类结果，搭建了Fisher 模型，为了实现预测功能，模型的测试集与训练集分别选取了相关性较强的过弯前1/4时长内的驾驶统计参数及过弯总时长内的统计参数。模型的预测精度达到76.5%误差总体向高风险倾斜，具有较大的应用价值。

除此以外，尚有一些值得进一步深入探讨的问题：

（1）模型的训练集的时间窗口长度选取值得将进一步探讨。

（2）样本数据量值得进一步拓展，从而得到更具有典型性的预测结果及工程建议。