上覆非饱和层地基-隧道动力响应半解析算法

郭慧吉，狄宏规，周顺华，王炳龙，何 超

（1. 同济大学道路与交通工程教育部重点实验室，上海201804；2. 同济大学上海市轨道交通结构耐久与系统安全重点实验室，上海201804）

地铁是缓解城市交通堵塞的重要手段之一。然而，随着地铁运营里程的快速增长和运营时间的增加，地铁隧道的车致振动问题日益突出，其不仅影响邻近建筑物内居民的生活以及精密仪器等的正常工作，还会诱发结构损伤和地基土的沉降。如何预测地铁隧道的车致振动响应和减小车致振动的影响，正受到越来越多的关注。

地铁盾构侧穿高速铁路桥梁桩基施工技术与应用…………………………………………………… 常富贵（12-204）

相关学者对此展开了研究，Metrikine 等［1］采用解析的欧拉梁模型来研究地下铁道的振动响应问题，尽管其可进一步考虑地基饱和特性以及分层特性［2］，但该系列模型为二维模型，无法准确获得系统三维动力响应。基于Flügge 薄壁圆柱壳振动方程，Forrest 和Hunt［3］提出了全空间地基‒隧道的管中管模型，即PiP 模型。随后相关学者考虑地基土体的饱和特性［4］，进一步发展了PiP模型。尽管PiP模型计算效率高，但该系列模型忽略了地表边界对系统动力响应的影响，适用于深埋隧道。Yuan 等［5］、He等［6-7］考虑地表边界的影响，利用波函数转化法，分别求解了单相弹性地基、饱和分层地基以及双洞隧道等条件下地基‒隧道系统动力响应闭合解。

然而，尽管上述模型可以较为精细考虑隧道结构、车辆荷载等对系统动力响应的影响，但上述计算模型均采用单相弹性、饱和多孔介质来模拟地基土体。事实上，对于饱和软土地区，由于蒸腾作用、地下水资源开发等原因［8］，饱和地基上部往往存在非饱和层，因此有必要考虑饱和度对系统动力响应的影响。基于非饱和土波动方程，徐明江等［9-10］，郭鹏飞等［11］先后考虑了土体饱和度对路基及桩基等结构动力响应的影响。随后狄宏规等［12］、郭慧吉等［13］考虑土体的非饱和特性，分别建立了非饱和全空间与非饱和半空间地基-隧道系统动力响应半解析解。但尚未考虑地基土的层状特性，也无法考虑上覆非饱和层对地铁隧道系统动力响应的影响。

为此，本文提出一种考虑上覆非饱和层的饱和地基‒隧道系统动力响应半解析算法。将上覆非饱和土体视为由固、液、气三相组成的介质，下部饱和地基土体视为由固、液两相组成的饱和多孔介质，隧道仍视为Flügge 薄壁圆柱壳。基于Helmholtz 矢量分解定理求解上覆非饱和土的波动方程与下部饱和土的波动方程（通过前述非饱和土波动方程退化得到），并采用分离变量法求解壳的振动控制方程，基于平面波和柱面波的转换性质，利用土层分界面、地表和隧道‒土体界面处的边界假设，建立了上覆非饱和层的饱和地基‒隧道系统动力响应半解析解，并探讨了上覆非饱和层对系统动力响应的影响。

1 模型的简化与假设

1.1 模型的简化

采用均质、各向同性、线弹性材料的Flügge薄壁圆柱壳模拟隧道衬砌，采用半空间或基岩上覆盖水平层状的不同类型介质（两相饱和多孔介质或三相非饱和介质）模拟地基土体。各层土体具有独自的坐标系，如图1所示，详细坐标系定义如下：

当下部为基岩时，根据模型边界及界面假设（3）可得

（2）隧道穿越土层中存在圆柱坐标与直角坐标两种坐标系，坐标原点设于隧道中心处。

图1 中，x（1）、x（2）、x（3）分别代表隧道穿越土层上方、隧道穿越土层以及隧道穿越土层下方独立坐标系中x的量值；Ι、Ⅱ分别代表隧道穿越土层上方、下方的水平土层交界界面。

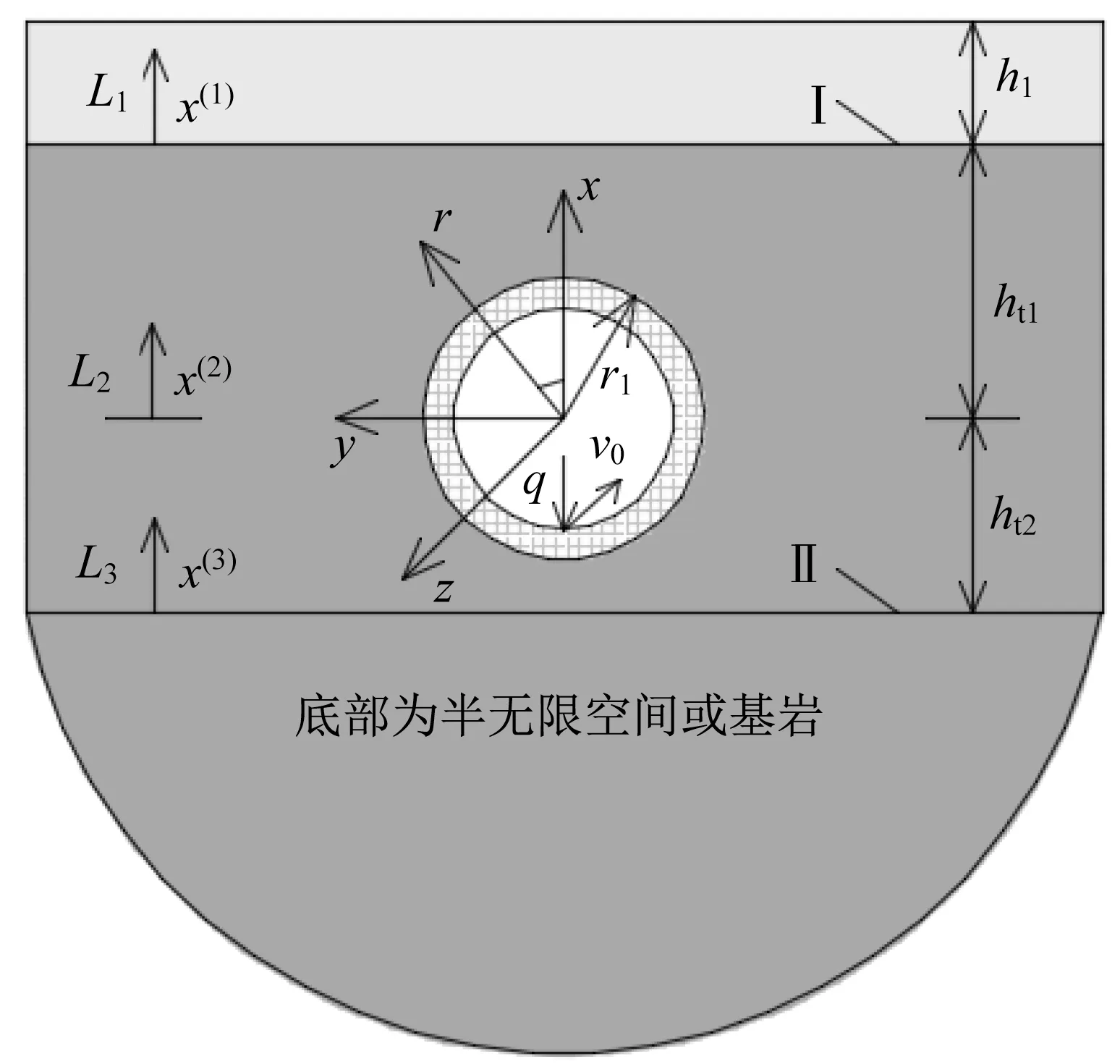
图1 层状地基‒隧道系统简化示意图Fig.1 Simplified schematic diagram of layered foundation-tunnel system

1.2 模型边界及界面假定

经上述简化后，对模型的边界（地表与模型下边界）与界面（隧‒土交界面及Ι、Ⅱ土层交界面）做出进一步假设，即

（1）地表边界应力为0，同时地表边界为透水、透气边界；

（2）当模型下部为半无限空间，则无限远处位移、应力、孔压等消散为0；当下部为基岩时，模型下边界基岩内位移为0，且不透水不透气。

“博看书屋”栏目为校内用户提供了大量的期刊、图书、报纸等数字资源的在线阅读和订阅服务，能满足读者对各类型阅读的需求。

高职院校主要目标是培养职业能力较强的人才。酒店英语是一门联系实际应用的一门课程，具有目标明确、应用广泛的特点，因此要注重学生实践能力的培养，其中包括专业英语交际能力、礼仪服务能力、岗位实践能力和环境适应能力。

（3）土层交界面Ι、Ⅱ处，土体位移、应力、孔压以及渗流连续。

（4）隧‒土交界面位移应力连续，且隧道衬砌不透水、不透气。

2 土体总场表达式的求解

将式（2）代入式（1），可在频域‒波数域中解得直角坐标系以及圆柱坐标系下位移̂、孔压̂、应力势函数分别为，具体求解过程参考文献［13］。

式中：下标“s”、“b”、“l”、“g”分别表示土颗粒、土骨架、孔隙水以及气体的分量；上标“'”、“''”分别表示对时间t求一阶、二阶导；ub、v、w分别为土骨架位移、孔隙水与土体骨架的相对位移、气体与土体骨架间的相对位移；λ、μ为土骨架Lame 常数；其余变量表达式及物理意义参考文献［13］。

如何更高效地传递建设经验，在大量建设的过程中实现全面而有效的管控？在全球经济一体化建设进程不断加剧与城市化建设规模持续扩大的推动作用下，制造行业在整个国民经济建设发展中所占据的地位日益关键。信息化、产业化以及科技化已成为整个现代制造行业建设发展的必然方向与趋势，数字化设计系统在这一过程当中所起到的重要作用不可忽视。数字化、信息化与建筑业的融合发展也已成为工程设计行业发展的方向。目前，在工程建设行业领域，不少行业已经探索或尝试了很多年，包括石化、电力、冶金行业的一些单位，取得了不少成绩。

首先引入三相非饱和多孔介质的实用波动方程［13］，即

根据Helmholtz矢量分解定理，式（1）中位移ub、v、w，可表示为

经过非饱和介质参数退化，即当Sr、Se趋近于1，As趋近于0时，式（5）、式（6）也可以表示两相饱和多孔介质总场。

1、幼虫钻蛀稻杆，因为害部位和生育时期的不同表现而不同。初孵幼虫危害集叶鞘内取食内壁组织，造成枯鞘。2龄后开始蛀入稻茎为害，分蘖期造成枯心，孕穗期造成枯孕穗，抽穗期造成白穗，灌浆成熟期造成虫伤株。幼虫常群集为害，钻蛀孔圆形，孔外常有少量虫粪，一根稻杆中常有多头幼虫，多者可达数十头甚至过百头，杆内虫粪较多。一般一头幼可危害3—5株水稻。

由模型简化可知，地基上部为三相非饱和介质，下部为两相的饱和多孔介质，因此地基土体总场表达式的求解思路为：首先通过非饱和土波动方程求解获得三相非饱和介质的总场表达式；再通过三相介质参数退化，获得两相饱和介质的总场表达形式，具体求解如下：

式中：上标“^”、“—”、“～”分别代表z方向对应的波数域、y方向对应的波数域以及时间t对应的时域；上标d，u分别代表下行波与上行波分量，o，r分别代表外行波与内行波分量，下标中1、2、3、4、5 分别代表SH、SV、P1、P2、P3 波分量，m表示模态分量，式中变量具体表达式参考文献［13］。

随着素质教育改革的不断推进，我国外语教学越来越注重学生交际能力的发展，但迫于升学和考试的压力，外语教学必须兼顾学生外语交际能力和外语应试能力都得到提高的双重任务。传统的外语教学方法很难让所有的学生同时获得相应的外语交际能力和应试能力。在外语教学中许多教育工作者都在积极寻求新的教学方法，进行教学改革尝试。预制性词块教学法作为一种新的教学方法可以满足这两方面的需求。

由于模型中存在不同形状的散射面（土层水平界面、隧‒土交界的圆形界面），导致地基土体中同时存在平面波与柱面波。故根据式（3）、式（4）可得不同位置处的位移̂、应力̂、孔压̂总场表达式如下：

式中：下标“SH”、“SV”、“P”分别表示SH、SV、P 波的分量；φ、ϕ、χ表示土骨架、孔隙水以及气体的势函数；ez为z方向上的单位向量。

3 模型耦合求解

在平面波、柱面波转化的基础上，进一步代入边界、界面条件进行模型的耦合求解。

为了满足不同类型波函数在边界或界面处的耦合求解，通过波函数转化公式，推导可得上行波、下行波与柱面外行波之间的转化关系（7）以及内行波与上行波、下行波之间转化关系（8）：

3.1 地表边界

根据模型边界及界面假定条件（1），可得

拙庵，徐州人，名智朴。 少曾过江，参百愚斯(净斯)大师于青浦之青龙隆福寺。 受记百愚。 实为洞宗第三十世。 辛亥(1671)北游，爱盘山丘涧，因止其地。[3]

担任兼职班主任的专业教师通常比较年轻，无论在工作上还是在生活上都富有激情，也乐于与学生一起活动，而且组织的活动通常比较接近年轻人的喜好，便于学生参加、融入，有助于师生沟通。同时也能在活动中通过言行起到模范带头作用。

热释电模块工作原理：当人体红外传感器感应到有不速之客进入到监控范围时(检测范围为6米)。传感器检测人体辐射的红外线，它将其转化为微弱的电信号。信号处理器对电信号进行处理、分析后，会输出高电平到MCU。MCU会分析具体的情况，当情况满足报警条件时，它给报警电路发送相应的报警指令。报警电路会控制声光报警器报警。同时MCU通过串行口通信接口RS232，控制GSM短信模块把相应的情况以短信的方式发送到用户手机上。通过上述过程来实现防盗防气体泄漏报警。

3.2 模型下边界

根据模型边界及界面假定条件（2），将模型下边界分为以下两种情况进行讨论，即

（1） 半无限空间

由于桩后土拱与桩侧土拱均为合理拱轴线，上述的力学模型对两者均可适用，下文在使用式(3)、式(4)时，仅需调整相对应的符号，公式形式并无改变。

若模型下部为半无限空间，则无限远处位移、应力、孔压等消散为0，故

（2） 底部为基岩

若模型下部为基岩，则基岩与土体交界面位移为0，且不透水、不透气，可得

3.3 土层界面Ⅰ

由图1可得，土层界面Ⅰ为水平界面，为实现总场势函数在土层界面Ⅰ处的耦合求解，需将总场表达式统一为直角坐标系的表达形式，故将式（7）代入式（6）。可得当x(2)＞0 时，直角坐标系下总场势函数的表达式为

根据模型边界及界面假定条件（3），结合式（13）可得

3.4 土层界面Ⅱ

同理为满足土层界面Ⅱ处的耦合求解，可得当x(2)＜0时，总场势函数直角坐标系下的表达式为

参考模型下边界求解，土层界面Ⅱ处的求解同样可以分为以下两种情况进行讨论。

（1） 半无限空间

当下部为半无限空间时，根据模型边界及界面假设（3）可得

超导磁场储能技术内环控制的终极目标是完成实时化有功与无功确定值,从而将功率调控后的给定值转化能得到超导磁场储能技术下的预测参数t和s值,可互相转换。

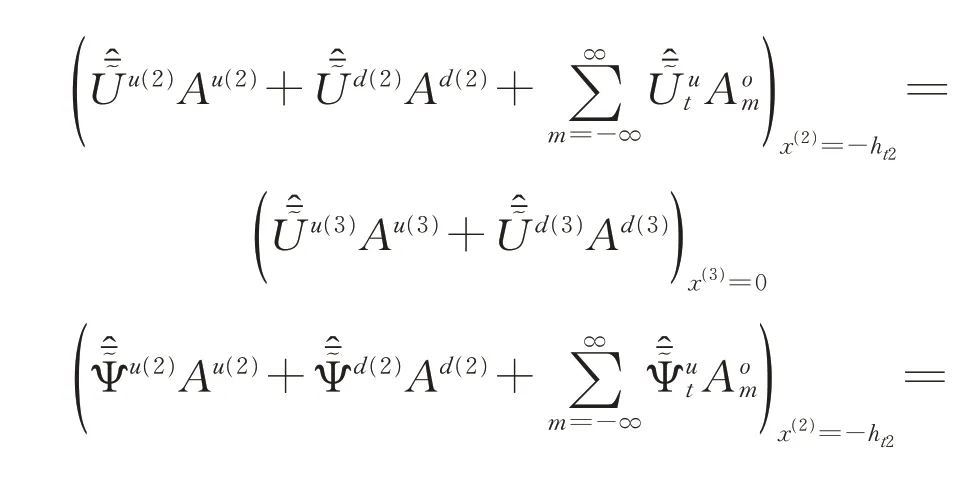
（2） 底部为基岩

（1）隧道穿越土层上方（下方）土层采用直角坐标系，且坐标原点位于土层底部（顶部）；

3.5 隧-土交界面

由图1 可得，隧‒土交界面为圆柱面，为实现总场势函数于隧‒土交界面处的耦合求解，需将总场表达式转换为圆柱坐标系的表达形式。

试验地位于广西南宁市广西大学林学院苗圃实验基地的温室大棚内，选用广西国有七坡林场1年生优质美丽兜兰进行光照试验，用蕨根、树皮作为基土进行育苗，底部放入少许沙石，利于排水和透气，每月定期施肥培育，待培育90 d后，选取生长一致的美丽兜兰进行试验。

首先联立式（15）、式（18）、式（20），可得直角坐标未知系数与圆柱坐标未知系数之间的转化关系，即

4 模型验证及算例分析

4.1 模型验证

为验证模型正确性，将上述模型退化为非饱和均质地基以及单相弹性分层地基模型分别与既有的半解析法模型［13］以及2.5D 有限元边界元模型［14］的计算结果进行对比分析，算例验证简化示意图如图2所示。

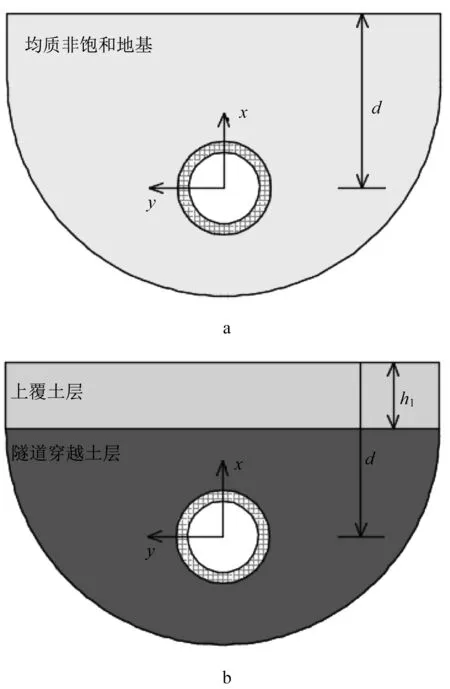
图2 验证算例示意图Fig.2 Verification Cases

验证算例①：将本文模型退化为非饱和均匀地质，如图2a所示。采用文献［13］中计算参数，计算饱和度为0.9，隧道埋深为10m的情况下，固定单位简谐荷载作用于隧道仰拱处时系统的动力响应。取隧道底部（‒3m，0m，0m）以及正上方地表位置处（10m，0m，0m）的计算结果与既有的半解析法模型进行对比分析，结果如图3所示。对比结果表明两者吻合较好，验证了本文方法的正确性。

验证算例②：计算隧道埋置于分层半空间地基土体内的情况，如图2b所示。隧道埋深为20m，上覆土体厚度为5m或10m。通过参数退化，获得验证模型的计算参数。计算固定单位简谐荷载作用于隧道仰拱处的动力响应，取隧道正上方地表位置处（20m，20m，0m）的计算结果进行对比分析，如图4所示。结果发现本文计算结果与既有2.5维有限元边界元模型［14］计算结果吻合较好，进一步验证了本文方法的正确性。

图3 验证算例①计算结果Fig.3 Comparison of calculation results of verification Case ①

图4 验证算例②计算结果Fig.4 Comparison of calculation results of verification Case ②

4.2 算例分析

通过算例分析，研究固定简谐荷载作用下上覆土体饱和度对地基土‒隧道系统动力响应的影响。隧道衬砌采用上海地铁盾构隧道结构形式［4］，地基土体上覆土层厚度为5m，地基土体分析类型为砂土，具体参数如表1 所示。不同算例土层饱和度取值如表2所示。

表1 算例分析计算参数Tab.1 Calculation parameters of calculation cases

表2 不同算例土层饱和度Tab.2 Soil saturation of different calculation cases

图5 给出了隧道仰拱处作用固定简谐荷载时，不同算例土体竖向动位移幅值随荷载激振频率的变化曲线。由图5可以发现不同算例的响应曲线存在差异。其中由图5 a 可以发现，案例1、2、3的响应曲线基本相似，由此可得隧道底部响应受上覆土体饱和度影响较少，其主要受隧道穿越土层土体性质的影响。图5b、5c中案例2、3与单一土层的案例1、4、5存在差异，由此可见上覆土体饱和度性质的变化会对地基土体内动力响应产生影响。

图5 不同位置处位移频响曲线Fig.5 Frequency response curves of soil displace⁃ment of differnt positions

为进一步研究上覆土层性质对地表振动位移临界速度的影响，图6 给出了移动恒定荷载作用于隧道仰拱处时，地表位置处（10m，0m，0m）以及（10m，20m，0m）不同算例下土体动位移幅值随荷载移动速度的变化曲线。可以发现，土体动位移幅值随荷载移动速度增大，出现峰值现象，即存在土体临界速度。通过对比不同算例临界速度大小发现，上覆土体饱和度的变化对土体临界速度的影响较小。而隧道穿越土层饱和度的变化会引起临界速度的改变，且隧道穿越土层饱和度越小，临界速度越大。

图6 不同算例临界速度对比分析Fig.6 Comparative analysis of critical velocity of different calculation cases

5 结论

（1）提出了上覆非饱和层的饱和层状地基隧道系统动力响应的半解析算法。该方法的计算结果与既有的2.5 维有限元‒边界元法的计算结果吻合较好，验证了本文方法的正确性。

（2）上覆土体性质的变化对隧道底部动力响应影响较小，但对地表响应影响较大。在进行地铁车致振动响应计算时，有必要考虑上覆非饱和层对系统动力响应的影响。

将理论模型中参数赋值后即可模拟目标价格变动对市场均衡及社会福利的影响。上述理论模型涉及9个参数，其中3个参数需要使用计量经济学方法估计获得，分别是试点区和非试点区供给弹性以及替代弹性，本文将借鉴前人的研究结果，其他6个参数可以根据变量的初始值计算获得(见表2)。

（3）系统临界速度受上覆土层饱和度的变化影响较小，其主要受隧道穿越土层饱和度的影响，且隧道穿越土层饱和度越小，临界速度越大。