基于NSGA-3与改进贝叶斯网络模型的测试优化选择方法
韩露, 史贤俊, 翟禹尧
(海军航空大学 岸防兵学院, 山东 烟台 264000)
测试性是描述系统健康状态可监控和可测试难易程度的一种设计特性。针对装备的电子设备开展测试性设计,可提高装备的故障检测与隔离能力,减少重大事故的发生。在测试性设计过程中,确立装备测试性模型后,需要针对模型进行测试优化选择,其目的是得到最佳的测试组合。测试优化选择需要综合考虑很多因素,如故障检测率、隔离率、虚警率、漏检率、测试成本等,从而以最低的成本满足测试性需求。
测试优化选择是一种基于测试性模型的多目标优化问题。现阶段大多学者的研究是基于相关性模型,这种模型又可依据是否考虑到不确定信息划分为2种,第一种模型不考虑不确定信息,即认为故障、测试间的关系是确定的;另外一种考虑到不确定信息,认为故障测试间的关系是不确定的,测试是不可靠的。针对第一种相关性模型,雷华军等建立了测试优化选择的数学模型[1],同时提出了一种改进的量子进化算法解决问题,算法收敛速度快,不会陷入局部极值;吴新锋等提出了改进二进制粒子群遗传算法,用粒子群进化代替了代间复制,提高了算法搜索效率[2];苏永定等构造了衡量测试集优劣程度的启发式函数,结合遗传算法提出了一种用于测试选择的遗传搜索算法[3];宋森森首次应用引力算法求解测试优化选择问题,并对其进行了改进[4]。针对第二种相关性模型,张贞对5种优化算法进行了分析,指出了分组编码遗传算法更适合解决电子系统测试选择问题[5];叶晓慧等综合了许多故障因素,提出一种动态贪婪算法求解问题,适合于大型复杂系统的测试性设计[6];张士刚针对NP问题,提出采用遗传算法与拉格朗日松弛算法进行求解[7];当前基于贝叶斯网络模型的测试优化选择研究较少,其中陈希祥提出了一种解决方案,其在贝叶斯网络模型基础上获取故障-测试相关性矩阵,后利用混合二进制粒子群-遗传算法求解问题[8],本质上该优化算法依旧基于相关性模型,贝叶斯网络的作用主要为计算含有不确定信息的故障-测试矩阵。
目前针对测试优化选择的方法具有2个明显的特征:①大都基于相关性模型开展工作;②将多个优化目标糅合成一个单目标进行研究,这些都带来了一定的局限性。相关性模型简单但处理不确定信息能力差,且不具备学习能力,后期模型更新困难,而贝叶斯网络模型不存在以上问题;其次单目标优化算法显然也无法得到多目标优化问题的最优解。
据此,本文引入了改进贝叶斯网络模型,模型建模难度降低,结构接近实际物理结构,方便进行测试优化设计。并提出基于改进贝叶斯网络模型与NSGA-3的测试优化选择方法,通过NSGA-3的种群概念来确立贝叶斯网络的结构,通过贝叶斯方法进行参数学习,确立条件概率表(conditional probability table,CPT)信息,进而利用模型计算测试性评价指标。应用该方法可得到一组非支配解(Pareto最优解),解决测试性设计过程中测试优化选择问题。
1 改进的贝叶斯网络测试性模型
1.1 贝叶斯网络测试性模型
贝叶斯网络是一种带有概率注释的有向无环图,可以表示变量间的相互关系与联合概率分布,可以据此特性建立贝叶斯网络测试性模型来描述故障变量与测试变量间的关系,模型示意图如图1所示,模型主要由以下元素构成:
故障有限集:F={f1,f2,…,fm};
可用测试的有限集:T={t1,t2,…,tn};
故障-测试相关关系P:条件概率表(CPT);
有向无环图:GDA={F,T,P,E},其中E为连接线,表示变量间具有相关关系;

图1 贝叶斯网络测试性模型
图中f1,t1的CPT信息如表1和表2所示。

表1 f1节点的条件概率表
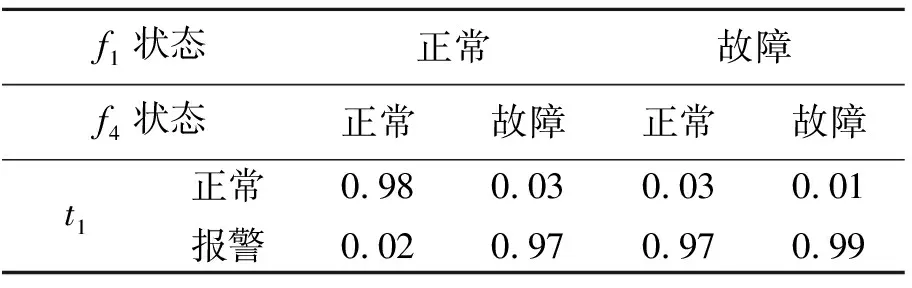
表2 t1节点的条件概率表
贝叶斯网络模型在不确定信息表达、概率推理、先验信息利用、模型自学习更新等方面具有优势,但在测试性建模过程中较少被采用,究其原因主要是直接表示故障、测试相关关系,结构复杂,计算量大,对数据量要求高;模型结构偏离实际物理系统,模型类似于黑箱,难以基于模型开展针对性的测试优化设计,且由于结构偏离,部分指标计算困难,如误诊率,对数据利用率相对不高。
1.2 改进的贝叶斯网络模型
根据前面对贝叶斯网络模型的分析,为改善模型性能,提出了改进的贝叶斯网络模型。该模型融入了多信号流图模型的信号思想,以信号节点替代测试节点,原有的故障、测试相关关系转变为故障、信号相关关系。连接线连接各信号节点,模型以此方式表征信号传递。某型装备的多信号流图模型如图2所示,该装备的改进贝叶斯网络如图3所示。

图2 多信号流图模型示意图

图3 改进的贝叶斯网络模型
改进的贝叶斯网络模型由以下元素构成:
故障有限集:F={f1,f2,…,fm};
故障-测试相关关系P:条件概率表(CPT);
有向无环图:GDA={F,S,P,E},其中E为连接线。
1.3 确立模型结构
1) 捋清故障源,确立每个故障源所含有的故障信号,将故障源与信号关联起来;
2) 确定故障信号传递路径,即不同故障源所含有的故障信号间的联系,将同一路径上的信号关联起来;
3) 将故障源作为故障节点,故障信号作为信号节点,关联关系用连接线E建立,由此贝叶斯网络结构初步确立;
4) 获取测试选择方案,此时信号节点分为2种:①节点处布置有测试;②节点处未布置测试;
5) 由前至后,将未布置测试的信号节点删除,将其父节点依信号传递路径,连接到下一个信号节点,其中信号传递路径也是故障传递路径;
6) 全部未布置测试的信号节点删除后,贝叶斯网络结构确立,某型装备的结构确立过程如图4所示。

图4 某型装备的模型结构确立过程
1.4 确立模型参数
改进的贝叶斯网络模型的结构根据测试选择而确定,模型结构确定后,进行贝叶斯网络参数学习,即利用给定的故障样本数据去学习网络的概率分布,最终得到节点的CPT信息,进而建立完整模型,后续可利用该模型计算测试性指标。
1.4.1 故障、测试样本数据
1) 装备正常运行过程中,监测测点位置的信号,在多数情况下,信号随机误差服从正态分布;
2) 根据测点处待选测试的性能,确定测试阈值。后进行故障注入实验,故障在测点处以信号的形式反映,超出阈值,则该测点处的备选测试检测到故障。将故障、信号信息记录到样本数据中,遍历所有可选测试,得到一条样本数据。
3) 重复上述过程,得到故障、测试样本数据集。样本数据集中还含有部分无故障状态下的信号信息,获取方式同步骤1)、2)。
信号随机误差分布与测试阈值的关系如图5所示,数据集如表3所示。

表3 故障、测试样本集

图5 信号分布与测试阈值关系图
1.4.2 参数学习
采用贝叶斯方法进行参数学习,该方法可以有效综合先验知识与样本数据来更新参数。方法简述如下。
(1)
(i=1,2,…,n;j=1,2,…,qi;k=1,2,…,ri)

给定样本集D=(D1,D2,…,Dm),D的一个元素Di表示样本的一个观测值,为一个案例。贝叶斯网络参数学习实质为给定样本D,计算后验分布p(θs|D,Sh)。

(2)
p(θij|Sh)服从先验Dirichlet分布Dir(θij|αij1,αij2,…αijri),得到后验分布
(3)
参数向量θs计算完毕,利用θs对案例进行预测,如预测案例DN+1
(4)
信号节点通过上述参数学习得到CPT信息;而故障节点CPT信息是在完成参数学习后,通过先验知识直接给出。究其原因为组件故障率相对于正常状态来说是极低的,而考虑到学习效率,样本数据是主要由故障状态下的数据组成的,参数学习得到的故障节点故障率是极度偏高的,因此需要在完成参数学习后,再通过先验信息给出节点CPT来进行替换。
1.5 测试性指标计算


(5)
系统对故障fj的故障检测率为FDRj
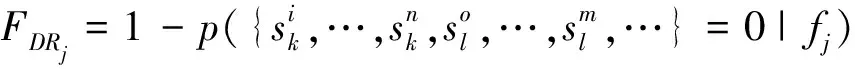
(6)
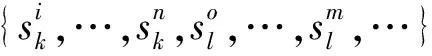
系统的故障检测率FDR

(7)
系统的故障隔离率FIR
(8)
故障虚警率FAR
(9)
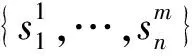
由于改进贝叶斯网络模型的信号节点,可以据此计算系统的故障误诊率
FMR=

(10)
测试成本C
(11)
式中:C(ti)表示执行测试ti的成本;Tc表示被选中的测试集合。
2 NSGA-3优化算法
从测试性指标方面看,测试优化选择问题是一种多目标优化问题,需要确定使得多项测试性指标达到综合最优的一种方案。NSGA-3算法[9-11]是一种多目标优化算法,由于其解决了NSGA-2存在的收敛性与多样性不理想的问题,可以更好地解决这种多目标优化问题。
2.1 Pareto最优解
NSGA-3算法最后得到的解是Pareto最优解。以最小化问题为例,该解集定义如下:
对于任意2个决策变量xa,xb∈xf,xf为可行解集合:
1) ∀i={1,2,…,k}:fi(xa)≤fi(xb)
2) ∃i={1,2,…,k}:fi(xa) 当且仅当满足以上2个条件时,称xa支配xb。在决策空间中,存在一个决策向量集X,X不被任何决策向量支配,则X称为Pareto最优解。 NSGA-3引入了参考点来更好地执行精英保留策略,使得解在目标空间内更加均匀,其概念及计算方法如下: 利用边界交叉构造权重的方法在超平面上均匀地产生C个点,这些点就是参考点。设置方法如图6所示。NSGA-3算法通过个体关联参考点的方法来衡量目标空间的均匀程度。 图6 参考点示意图 参考点是建立在超平面上的,超平面计算方法简述如下: 1) 标准化:首先选取当前种群中每一维目标函数的最小值,计算出理想点,以理想点为原点,以目标函数为坐标轴,根据(12)式将个体标准化; 3) 依据这些极值点构建超平面,超平面与坐标轴的交点即为截距ai,超平面如图7所示。 图7 超平面示意图 (12) (13) 个体关联参考点的方法如下: 1) 构建参考点向量,即坐标系中参考点到原点的连线; 2) 对种群中每个个体遍历参考向量,找到距离个体最近的参考点,记下关联信息与距离,个体与参考点完成关联,关联描述如图8所示。 图8 个体关联参考点示意图 1) 确定种群规模N,初始化种群; 2) 确立理想点,对所有个体的目标值进行归一化,计算出极值点,构建超平面,确定参考点; 3) 对种群进行非支配排序; 4) 用遗传算子对种群进行操作,得到规模为N的子种群; 图9 NSGA-3算法流程图 5) 合并2个种群,得到规模为2N的种群,并进行快速非支配排序,确定非支配层级; 6) 按照非支配层级由小到大的顺序依次将个体加入下一代种群中,直至种群规模为N,此时的非支配层级为L; 7) 由于多数情况下L层的个体无法全部加入 中,需要在L层中选择一部分个体放入。首先将1~L层个体关联到参考点,然后寻找到关联1~L-1层个体最少的参考点,最后从L层中选择一个关联到该参考点的个体加入,重复执行该步骤,直至种群 规模为N,此时用种群 替换种群; 8) 重复步骤4)~8),直至完成规定代数,最终得到Pareto最优解,解码解集可得测试方案。 以导弹上的机载雷达某组件为例,该组件的结构示意图如图10所示,初步建立的改进贝叶斯网络结构如图11所示。 图10 组件的结构示意图 图11 雷达组件的改进贝叶斯网络模型 该组件的故障信息及部分故障、测试样本集如表4、表5所示,测试成本如表6所示。 表4 故障信息表 表5 故障、测试样本表 表6 测试成本表 系统测试性设计要求:故障检测率不低于95%,模糊度为1的故障隔离率不低于70%;测试优化选择选定4个目标函数:系统的虚警率A(x),系统的误诊率M(x),测试成本C(x),测点数量D(x),要求4个目标函数达到综合最小。针对该实例,测试优化选择问题的数学模型如(14)式所示。 (14) NSGA-3算法参数如表7所示,贝叶斯网络参数学习样本数量设置为2 000组。 表7 参数设置 执行算法后,得到非支配等级最高的Pareto解集如表8所示,同时记录该解集对应的测试性指标于表8中。 表8 Pareto解集及其对应的测试性指标 测试组合中1表示该测试被选择,0表示测试未被选择。侧重于不同需求,可从表8中选择不同的解作为测试优化选择方案,侧重于不同需求的测试组合如表9所示,研发人员可根据需求选取不同的测试选择方案。 表9 测试优化选择方案 本文阐述了改进贝叶斯网络模型,该模型将信号概念引入贝叶斯网络中,降低了贝叶斯网络的建模难度,也使得模型结构趋近于实际物理结构。同时,模型可发挥贝叶斯网络对不确定信息的表达和处理能力,测试性指标计算准确。模型在结构与指标计算方面都更有利于研究人员进行测试优化设计工作。本文改变了之前将多目标问题转化为单目标问题的做法,直接在改进贝叶斯网络模型的基础上,利用NSGA-3多目标优化算法计算测试选择方案,在案例中可以看到,算法得到的Pareto最优解给出了面向不同需求的测试选择方案。给出的方案也验证了本文方法的有效性与可用性。2.2 参考点及相关概念





2.3 NSGA-3算法实施步骤

3 实例分析






4 结 论

