水下智能航行体跟踪目标的自适应加权导引律设计
梁增顺, 冯西安, 薛昱
(西北工业大学 航海学院, 陕西 西安 710072)
航行弹道体现航行体对机动性能的需求,而导引方式直接影响航行体的弹道。目标的运动状态和导引方式是影响导引弹道的2个关键因素[1],不同导引方式通常使航行体按照不同的弹道接近目标。因此导引方式选取将直接影响航行体的弹道性能,是弹道性能最重要、最直接的影响因素之一[2]。
按照发展历程划分,导引方式可以分为古典导引方法和现代导引方法。古典导引方法通常有以下优点:需要的信息量少、结构简单和容易实现,因此被广泛采用[3]。但随着现代控制理论的发展以及海战对水下航行体的要求越来越高,基于现代控制理论的现代导引方法和导引律得到了广泛关注。陈嘉杰等[4]针对滑翔弹道终端的弹道倾角和位置约束,研究了一种鱼雷最优导引规律,并进行了仿真验证;李娟等[5]将障碍物防碰撞和饱和约束下的目标跟踪问题相结合,解决了环境未知下目标跟踪导引问题;杨惠珍[6]提出了基于扩张状态观测器的反鱼雷鱼雷拦截导引律,实现了一种含干扰补偿的ATT最优拦截导引律;叶慧娟等[7]基于目标和鱼雷在水平和垂直面投影的相对运动,设计了双滑模控制器,使得航行体在2个平面的视线角保持不变,达到精准攻击的目的;文献[8]设计了一种鱼雷的垂直命中导引方法,同时通过萤火虫算法对其进行了优化和仿真验证。
文献[9]根据目标运动状态和距离远近等信息,通过引入模糊控制方法自适应地调节线导鱼雷的导引参数,形成了一种基于模糊控制的串联导引方法,能够有效地将水下航行体导引到理想攻击阵位。但其并没有考虑制导信息估计精度这一因素,无法解决制导信息误差大对制导精度带来的影响。
本文综合固定提前角、扩展比例导引法和自适应滑模导引律对制导信息的需求差异和各自制导律的优点,给出一种基于模糊控制的水下智能航行体自适应加权导引方法。该方法将探测设备在目标跟踪过程中对目标位置、速度、方位和距离等制导信息的实时估计精度作为模糊控制器的输入,通过模糊权系数计算得到制导信息对应3种导引方式的权系数,构造随制导信息估计误差变化的自适应加权制导律,实现智能航行体的精准导引。
1 相对运动模型
航行体与目标的相对运动可分为水平面的相对运动和垂直面的相对运动,但针对智能航行体制导律的研究主要考虑水平面的相对运动。因此,本文仅在水平面方向开展对航行体导引方式的研究。假定航行体和目标为质点模型,相对运动关系见图1。
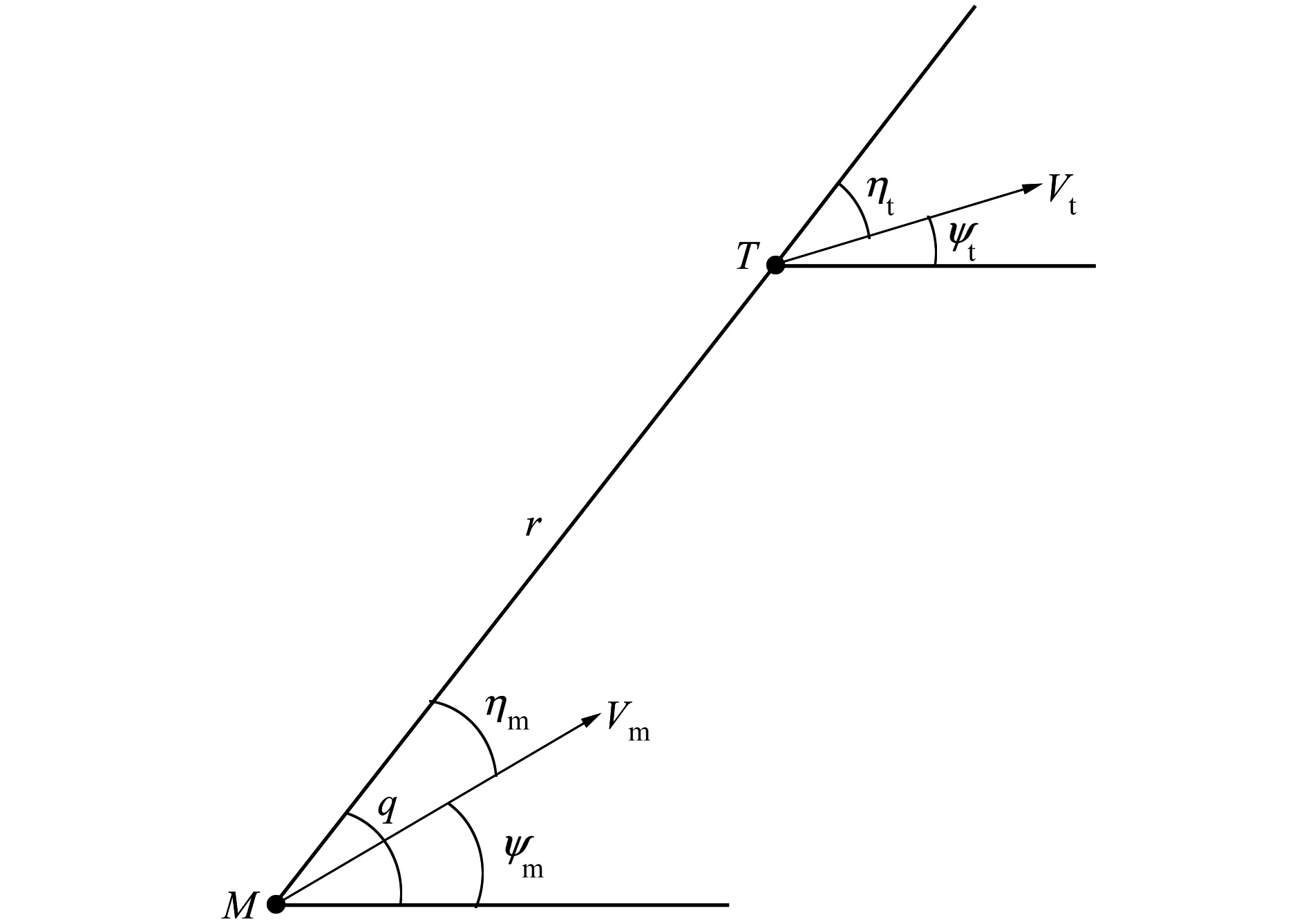
图1 相对运动坐标模型
则相对运动方程为
(1)
式中
(2)
am为航行体的法向加速度;vm,vt分别为航行体和目标的运动速度;r为航行体和目标之间的相对距离;ηm,ηt分别为航行体和目标的提前角;ψm,ψt分别为航行体的偏航角和目标的航向角;q为视线角。
2 典型导引方法
2.1 固定提前角
采用固定提前角导引法时,需要航行体自导装置测量目标的相对运动方向,以及视线相对提前角的偏差,再由控制系统按指令修正航行体的速度矢量。从工程实现的难易程度和攻击效果方面考虑,固定提前角是一种较为理想的导引方法。其主要优点是工程上易于实现,且航行体接近目标时舷角不等于零,增加了目标的有效尺寸。缺点是当目标机动时,跟踪目标效果较差,甚至可能丢失目标[10]。
固定提前导引法下智能航行体的法向加速度可表示为
(3)
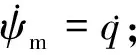
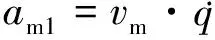
(4)
2.2 扩展比例制导律
比例导引法是一种具有普遍性的导引方法,通常易于工程实现,对低速、小机动目标有较好的制导性能,但对高速、大机动目标的攻击效果就相对较差[11]。为了提高比例制导律攻击大机动目标的能力,有学者已提出了在比例导引基础上引入非线性补偿的改进型比例导引方法,如扩展比例导引和广义比例导引等。
采用比例制导律导引攻击目标时,航行体速度矢量的转动角速度与视线角的转动角速度成正比。则比例制导律的导引关系式可表示为
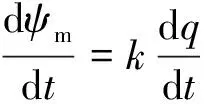
(5)
扩展比例制导律是在比例制导律的基础上,对导引系数和增加的偏置修正参数进行合理取值,以提高对机动目标的跟踪精度。其表达式为
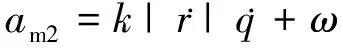
(6)
式中:k为导引系数;ω为偏置修正参数。

(7)
式中,at为在视线角垂直方向上目标加速度分量。
2.3 自适应滑模制导律
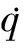

(8)
则自适应滑模趋近律为:
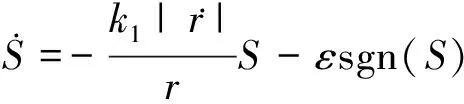
(9)
进一步便可推导出自适应滑模制导律在视线垂直方向的分量为

(10)
式中:k1为控制系数;sgn()为符号函数;ε取小的正数。那么,采用自适应滑模导引律时航行体在法向方向的加速度可表示为
(11)
2.4 3种导引方式优缺点比较
3种导引方式的设计思想不同,这使得所设计的制导律具备着不同的优缺点,如表1所示。

表1 3种导引方式优缺点对比
3 自适应加权制导律
固定提前角、扩展比例制导律和自适应滑模制导律3种制导律的优缺点及所需制导信息的种类均存在差异,若能将3种导引方法有机组合,充分发挥各自优势,将能有效提高航行体的制导精度。下文将各制导律所需制导信息中与目标相关的部分简称为制导目标信息。如图2所示,得到3种典型制导律后,就需要对探测设备估计的目标信息进行分类,再根据模糊权系数计算得到目标信息估计后对应各类信息的权重,即各制导律的权系数,最后通过加权求和构造自适应加权制导律。

图2 自适应加权导引律设计框图
目标信息分类是基于3种航行体制导律对制导目标信息种类需求的不同进行分类。首先,给出3种制导律所需制导目标信息的种类,如表2所示。
根据表2将航行体通过探测设备估计的目标信息分为以下3类。若估计得到的制导目标信息精度较差,且不完整,这时可以采用需要制导目标信息较少的固定提前角导引方法,故将固定提前角所需的制导目标信息分为一类,记为A类;其次,如果自导过程中可以对目标视线角和相对距离的变化,以及目标机动法向加速度进行估计,且精度满足,便可主要采用扩展比例制导律进行制导,故可以将扩展比例导引律需要的制导目标信息记为B类;最后,将自适应滑模制导律所需的制导目标信息记为C类。

表2 各导引方式所需目标的制导信息
目标分类完成后,根据模糊权系数计算得到3种制导律对应的权系数,通过将权系数与各制导律加权求和得到自适应加权制导律。即
a=W1am1+W2am2+W3am3
(12)
式中,W1,W2,W3为3种制导律分别对应的权系数,且权系数满足W1+W2+W3=1。
4 模糊权系数计算
模糊权系数计算是指通过模糊估计方法计算目标信息分类后各类信息的估计精度量化值。对各类信息估计精度量化值的估计可分为2步:①对各类信息中包含的所有制导目标信息的估计精度进行量化;②将每类信息包含的制导目标信息中估计精度最差的量化值作为该类信息的估计精度量化值。
通常航行体会采用各种滤波算法对所需的制导信息进行估计,例如最常用的扩展卡尔曼滤波方法。估计精度可以通过估计的误差或估计的不确定度表示。但实际跟踪过程中目标的真实状态信息未知,无法得到估计的误差,只能通过估计的不确定度来表示状态的估计精度[13]。估计的不确定度大小等于状态估计协方差矩阵的迹[14],如估计位置状态的不确定度就等于目标位置估计协方差矩阵的迹。
本研究数据来源于 2000—2017年全国范围内部分城市降尘重金属的研究结果,所收集的数据涉及工业区和非工业区,为避免数据来源单一化,工业区包括矿区和冶炼区;非工业区包括商业区、文教区、居住区、交通区等,具体数据见表1、表2。
制导目标信息各模糊子集中心点的取值应主要考虑不同估计精度对制导律精度影响,同时与航行体所能达到的估计精度相结合。虽然航行体采用扩展卡尔曼滤波等算法对目标状态信息进行估计时,估计精度会受目标方位、距离、机动情况、探测设备精度、滤波算法初值等因素影响,但为方便研究,此处各制导目标信息模糊子集中心点取值设为定值。

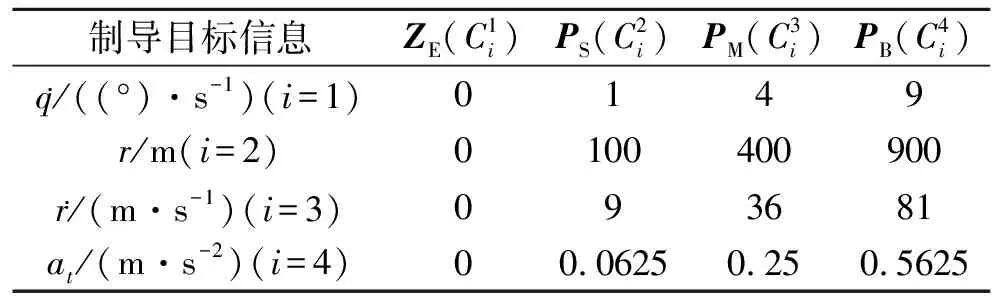
表3 隶属度函数中心点
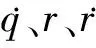
则xi对模糊子集ZE的隶属度μ1(xi)可表示为
(13)
xi对模糊子集PS的隶属度μ2(xi)可表示为
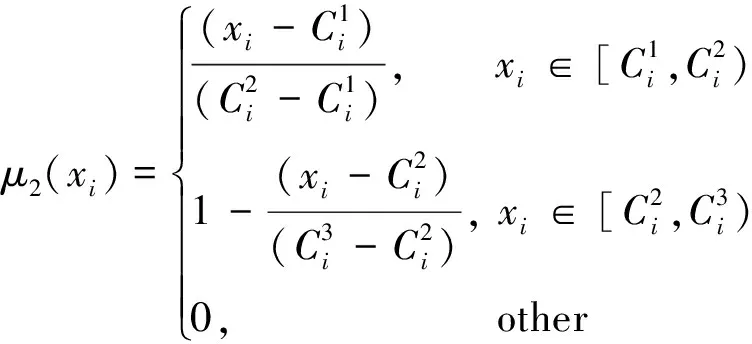
(14)
同理,xi对模糊子集PM的隶属度μ3(xi)表达式与(14)式类似。xi对模糊子集PB的隶属度μ4(xi)可表示为
(15)

(16)
制导律所需的制导目标信息种类可能不限于一种,例如扩展比例制导律和自适应滑模制导律均需要3种制导目标信息。因此,A,B,C 3类信息的估计精度量化大小就可以取每类信息所包含的制导目标信息中估计精度最差的量化值来作为该类信息的估计精度量化值。则A,B,C 3类信息的估计精度量化值ωA,ωB和ωC可以分别表示为
(17)
得到航行体目标信息估计结果对应各类信息的估计精度量化值后,再对3类信息的量化值进行标准化,得到3种制导律对应的权系数W1,W2和W3

(18)
5 仿真与分析
设自导开始时,航行体的初始位置为坐标原点,速度为40 kn,初始偏航角为30°;目标的初始位置为(1 000,1 500),速度为20 kn,初始航向角为10°;对于目标信息估计的误差,仿真中以高斯白噪声代替;视线角变化率、相对距离、相对距离变化率、目标法向加速度和目标提前角的真实值分别加入均值为0,标准差分别为2°/s,20 m,6 m/s,0.5 m/s2和2°/s的白噪声模拟目标信息估计误差;再分别采用3种导引律和自适应加权导引律进行500次Monte Carlo仿真,得到脱靶量ξ累积分布P的曲线。
扩展比例制导律的制导系数取k=3;自适应滑模制导律的控制系数取k1=3,ε=2;同时,取智能航行体的最大法向加速度max|am|=5 m/s2。
①仿真环境1:目标未采取机动,沿初始航向角航行;仿真的制导周期取T=1 s。
图3至6分别是目标未机动下3种导引方式理想情况下的轨迹曲线、4种导引方式下的航迹曲线、3种导引方式对应权系数变化曲线和脱靶量累积分布曲线。从图3可得,在目标未机动时,3种导引方式均能实现对目标的攻击;但结合图4和图6可以发现,在存在干扰的情况下,自适应加权导引律的轨迹曲线和脱靶量相对于其他3种导引律有明显优势。
②仿真环境2:为了躲避追踪和攻击,目标采取机动规避战术以0.5°/s向正北方向机动;仿真的制导周期取T=1 s。

图3 理想状态3种导引方式航行体-目标运动轨迹 图4 不同导引方式下航行体-目标运动轨迹 图5 各导引方式权系数变化曲线 图6 脱靶量累积分布
图7至10分别是目标机动下3种导引方式理想情况下的轨迹曲线、4种导引方式下的航迹曲线、3种导引方式对应权系数变化曲线和脱靶量累积分布曲线。从图7可以得到,在目标机动情况下,固定提前角很难实现对目标的有效攻击;但自适应加权导引律和其余2种导引律可实现对机动目标的攻击。从图8和图10可以看出,自适应加权导引律的航行轨迹和最终的脱靶量相对于其余3种导引方式都有较大优势,能更好的实现对机动目标的追踪和攻击。

图7 理想状态3种导引方式航行体-目标运动轨迹 图8 不同导引方式下航行体-目标运动轨迹 图9 各导引方式权系数变化曲线 图10 脱靶量累积分布
6 结 论
制导过程中,由于航行体对制导律所需目标状态信息的估计精度受各种因素影响,导致智能航行体的制导精度下降。为了减小估计精度对制导精度的影响,本文分析了固定提前角,扩展比例导引律和自适应滑模导引律3种导引方式的优缺点和所需制导目标信息的种类差异,将提供的目标信息分为A,B,C 3类,然后通过基于三角形隶属度函数的模糊方法计算各类信息的权系数,构造了自适应加权导引律。该制导律能够根据各类信息的估计精度量化值计算得到相应的自适应加权制导律,形成以制导目标信息估计精度作为模糊控制器输入的并联组合导引方法,这也为之后更为复杂的组合导引方法研究开辟了思路。
通过仿真分析得到,自适应加权导引律在目标未机动和目标机动的2种仿真环境下,其对应的智能航行体弹道轨迹和最终的脱靶量都要优于其他3种导引方式。若定义脱靶量小于10 m作为航行体命中目标的判断依据,通过2种仿真条件下脱靶量累积分布的结果可以得到,采用自适应加权制导律的智能航行体命中概率均能到达90%以上。与此同时,自适应加权导引方式能很好地根据智能航行体对目标状态信息估计精度,自适应地切换各制导律对应的权系数,得到相应的自适应加权导引律,实现航行体对目标的更佳跟踪。

