基于内聚力行为的复合材料 L型胶接接头分层扩展研究
拓宏亮, 卢智先, 马晓平, 郭宏宇
(1.长安大学 理学院, 陕西 西安 710064; 2.西北工业大学 航空学院, 陕西 西安 710072;3.中国科学院 工程热物理研究所, 北京 100190)
复合材料胶接连接是飞机结构常见的连接形式之一,胶接是指将2个或多个构件通过胶粘剂连接在一起,具有结构轻、连接效率高、密封等优点,由于不需要沿厚度方向进行开孔,不会引起应力集中并能保持良好的气动外形[1-3]。胶接结构在服役期间将承受静力和疲劳载荷,易发生分层损伤,导致复合材料胶接结构的承载能力和连接效率下降,并进而影响复合材料结构的强度和完整性[4]。
针对复合材料的分层损伤问题,国内外学者已经做了大量研究,关志东等[5]建立了新型零厚度界面单元模型,通过试验验证模型的准确性。卢子兴[6]考虑了几何非线性变形行为和弹塑性非线性行为,建立了界面的非线性内聚力模型。喻溅鉴和周储伟[7]基于内聚力行为,考虑了裂纹闭合效应,发展了有效描述疲劳裂纹扩展的界面损伤本构关系。曾海艳等[8]通过试验研究了复合材料夹芯结构L型接头在弯曲载荷下的强度和疲劳行为,石好男等[9]基于复合材料渐进损伤模型和内聚力模型研究了L型胶接接头的损伤与失效机理。
Camanho等[10]提出了三维混合加载下的内聚力模型,计算精度较好。Harper和Hallett[11]研究了内聚力区域长度的影响,结果表明内聚力区域至少需要2~3个单元,且降低强度可以延长内聚力区域从而增加单元尺寸。Hu等[12]在内聚力模型中增加 “预软化区域”,该模型允许采用相对较疏的网格,具有较高的计算效率。Elmarakbi等[13]发展了自适应内聚力区域模型,可有效降低数值振荡现象。Khoramishad等[14]针对胶接接头的分层损伤扩展问题,发展了基于应变的双线性内聚力本构模型来研究胶接接头的分层损伤扩展问题。Turon等[15]结合断裂力学和损伤力学,建立描述复合材料静力和疲劳分层扩展的本构模型,该模型能准确预测静载下的分层扩展和高周疲劳分层扩展。Harper[16]基于静力分层模型,引入与Paris公式相关的疲劳损伤演化率,采用显式求解算法描述复合材料的疲劳分层扩展,并对复合材料的单搭接接头进行验证。Kawashita和Hallett[17]提出了基于全局节点坐标的裂纹尖端追踪算法,使用显式有限元软件建立新的疲劳损伤演化率。Amiri-Rad等[18]建立了复合材料高周疲劳分层模型,采用水平集法追踪三维裂纹尖端,结果表明该方法在处理裂纹扩展时优于VCCT方法。Al-Azzawi等[19]采用一种新的梯形牵引力-张开位移描述单调和高周疲劳载荷作用下的弹塑性行为,并通过DIC和声发射试验验证数值模型的准确性。
本文以复合材料L型胶接接头为研究对象,进行静力和疲劳试验,发展了基于内聚力单元的静力和高周疲劳分层扩展模型,改进疲劳分层扩展中能量释放率的计算方法,提高其计算精度,结合试验和数值结果,系统研究了L型胶接接头的分层损伤扩展和失效机理。
1 复合材料L型胶接接头静力和疲劳试验
复合材料L型胶接接头采用二次胶接连接,首先将L型加强筋和底板固化成型,再使用Loctite胶实现加强片和底板的胶接,胶层名义厚度为0.12 mm,试验件几何尺寸如图1所示,复合材料体系为T300/CYCOM 970,预浸料单层名义厚度为0.25 mm,L型加强筋的铺层为[-45/0/45/90]s,底板复合材料的铺层顺序为[-45/0/45/0/-45/0/90/0/-45/0]s,底板两侧和L型板上端采用加强片加强,加强片长度为40 mm,厚度为2 mm,试验件宽度为60 mm,静力试验采用INSTRON 8872电液伺服试验机,静力试验的控制方式为位移控制,加载速率为0.5 mm/min,为了减少试验结果的分散性,静力试验包含3件试样,试验过程中在试验件VL、VR和PL 3个位置布置应变片,其中PL位置为L型下端面的中心线位置,距A端12.5 mm,VL和VR对称贴片,距B点10 mm。

图1 L型接头试验件几何形状及应变片布置情况
图2a)为L型胶接接头试验件静力拉伸载荷-位移曲线,3件试验件承载能力基本相同,分散性小。初始加载阶段线性较好,达到最大载荷后,L型接头和底板接头处由于应力集中,胶接层开始起裂,此时试验中出现了清脆的响声,之后载荷迅速下降,随着位移继续加载,分层不断向前扩展,直至胶接面出现大面积分层,刚度显著下降,试验件失去承载能力,此时应变呈明显的非线性。

图2 试验结果曲线
图2b)为L型接头典型的拉伸应变-载荷曲线,可以看出L型加强筋垂直面两侧VL和VR应变不对称,由于结构不对称导致的应变分布的不均匀,其中VL一侧的应变较大,VR一侧的应变较小,L型加强筋水平面PL区域的应变较小,当载荷加载至1.4 kN后,应变均表现出非线性。
图3a)给出L型接头胶接试验件的静力破坏断口,L型板和底板倒角处存在富胶区域,该区域损伤区参差不齐,其他断口均较为光滑平衡,发生了胶结面的内聚破坏。
选取静强度的40%的应力水平进行疲劳试验,试验设备为INSTRON 8872电液伺服试验机,加载方式为等幅正弦波加载,加载频率为4 Hz,应力比为0.1,为了减少试验件的分散性,疲劳试验包含3件试样,其寿命分别为768 643,684 121和816 421,图3b)为典型试验件的疲劳破坏断口,和静力断口相比,断面更为光滑,疲劳加载下,在n/N=0.8~0.9时,出现疲劳分层扩展现象,扩展速度迅速,试验件发生疲劳破坏。

图3 破坏断口
2 分层本构模型
2.1 静态分层模型
本文建立的层间疲劳分层模型基于内聚力模型经典的双线性牵引力-张开位移本构模型。采用基于应力的二次损伤起始准则表征损伤起始
(1)
式中:τ3,τ1,τ2分别表示Ⅰ、Ⅱ和Ⅲ型分层损伤对应的应力;N,S和T则是相应的界面强度;〈·〉为Macaulay符号。
定义混合模式下的总相对位移为
(2)
混合型分层的损伤起始位移可根据二次应力失效准则计算,为

(3)

图4 混合型分层疲劳本构模型
采用B-K准则[20]表征分层损伤的演化
(4)
式中:GⅠC,GⅡC分别是Ⅰ,Ⅱ型断裂韧度,Gshear=GⅡ+GⅢ,GT=GⅠ+GⅡ+GⅢ,B-K准则中的参数η由试验参数拟合所得。
进一步推导出完全损伤时的最终失效位移
(5)
则混合加载模式下的分层损伤变量d可表示为
(6)
2.2 高周疲劳分层模型
考虑到复合材料分层疲劳扩展的复杂性,众多学者借鉴静力分层本构模型和表征金属疲劳裂纹扩展的Paris公式,发展基于内聚力模型的复合材料疲劳分层扩展模型。
该模型认为在疲劳载荷作用下,总的损伤d由静力加载下裂尖张开位移造成的损伤和循环载荷加载下的疲劳累积损伤两部分组成,其中静力加载下的损伤ds由2.1节计算所得,疲劳载荷导致的损伤df可结合损伤力学和断裂力学方法推导。
疲劳损伤变量d随循环次数N的变化率表示为
(7)

(8)


图5 疲劳加载下损伤区域和裂纹扩展的等效关系

(9)

(10)

(11)
(12)
式中,能量释放率变化幅值ΔG和最大能量释放率Gmax通过内聚力模型的本构关系获得。GC为混合加载下的总的临界能量释放率,C和m为材料常数,通过试验获取。
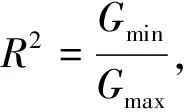

(13)
(14)

(15)

图6 能量释放率计算方法
(14)式通过内聚力双线性本构模型来确定能量释放率,当材料进入疲劳损伤演化阶段,该公式的计算方法精度较低,为了提高能量释放率的计算精度,本文采用图6的计算方法,通过对疲劳损伤本构下的实际面积进行计算,选取Turon[15,21]和Oliveriraer[22]的疲劳分层模型进行对比。如图7所示,修正后的模型明显提高了裂纹扩展速率的计算精度。

图7 修正模型后裂纹扩展速率的相对误差
3 数值计算
3.1 静力分层数值模型
基于ABAQUS/EXPLICIT模块建立复合材料L型胶接接头的三维有限元模型,L型板和底板均采用三维连续壳单元,沿复合材料厚度方向各子层布置一个单元,网格尺寸为1 mm×1 mm,胶接面采用内聚力单元,单元类型为COH3D8内聚力单元,为限制底板固定面的面外位移,L型板上端和试验件夹持区域施加位移边界条件。对胶接区域进行网格细化,搭接区域的网格沿纵向尺寸为0.2 mm,表1和表2分别给出了胶层和复合材料的基本力学性能参数。

表1 胶层基本力学性能

表2 T300/CYCOM 970基本力学性能

图8 试验和数值计算载荷-位移曲线对比
胶层静力分层本构模型基于VUMAT子程序实现,并植入到建立的数值模型,分别进行数值计算。试验和数值计算的载荷-位移曲线如图8所示,可见二者曲线吻合较好,表明模型能够较为精确地预测复合材料L型胶接接头的刚度和破坏载荷,失效载荷的预测误差仅为2%。
图9给出了位移加载至0.7 mm处的Mises应力云图,选取L型接头胶接面裂纹阶段进行局部放大,可见,L型加强筋、底板和胶层在分层阶段多存在明显的应力集中,从而导致其能量释放率变高,诱发分层损伤的起始。且对于L型加强筋,将其变形放大十倍,可观察到不对称拉伸载荷下,L型加强筋发生弯曲变形,靠近胶接面一侧凸出,另一侧凹入,VL一侧弯曲也导致了拉应变,故导致VL一侧应变明显较高,VR一侧弯曲导致了压应变,使得其拉伸应变降低。图10给出了L型接头搭接区域分层损伤云图,可以观察到分层损伤从胶接区域前缘开始,不断向尾部扩展,迅速贯穿整个胶接面,试验件的刚度发生下降,胶接接头失效。

图9 胶接接头的Mises应力云图及搭接区放大图
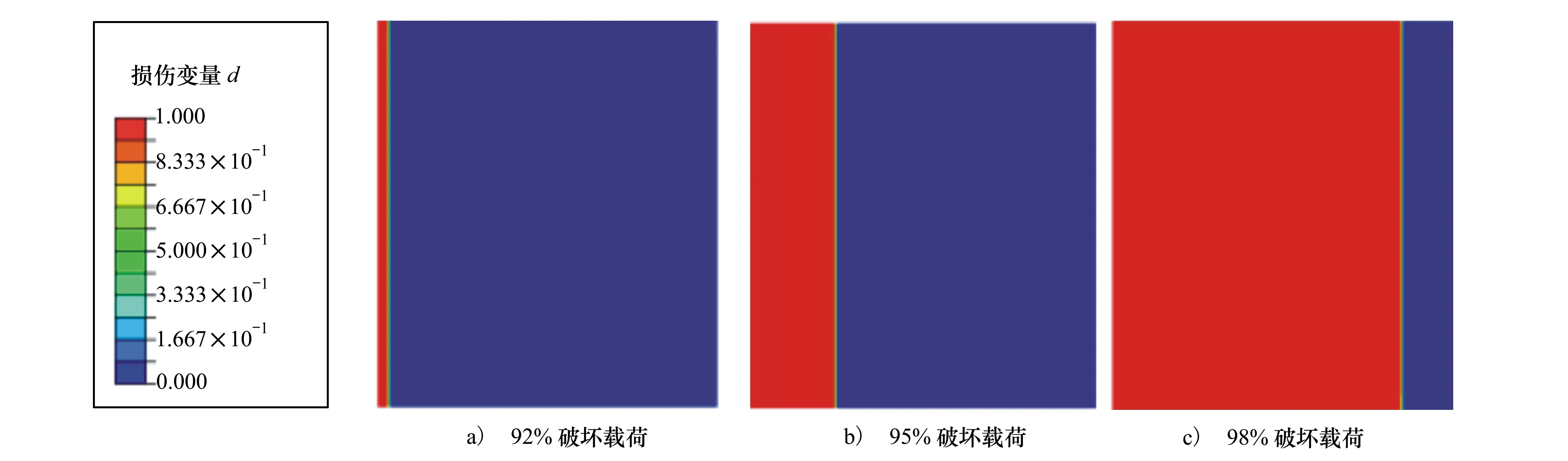
图10 分层损伤扩展示意图
3.2 疲劳分层数值模型
为提高疲劳分层模型收敛性,采用ABAQUS显式求解模块EXPLICIT建立复合材料L型胶接接头疲劳分层的有限元模型,由于疲劳试验结构形式和材料参数均与静力试验一致,故数值模型的网格划分和静力模型相同,为了验证疲劳分层本构模型的网格敏感度,分别采用0.2,0.4,0.6和0.8 mm网格计算I型和II型分层的裂纹扩展速率,如图11所示,计算结果表明采用0.2 mm网格,I型、II型分层的裂纹扩展速率和试验数据吻合较好。

图11 I型和II型分层裂纹扩展速率的网格敏感度
施加疲劳载荷时,为了提高计算的效率,分2个步骤加载,如图12所示,第一步将载荷加载至最大载荷,第二步保持最大载荷,为了提高计算的收敛性,ΔN选取为50。疲劳分层本构模型通过VUMAT子程序实现并植入到建立的数值模型。由于缺乏胶层混合加载的疲劳材料参数,疲劳参数根据文献[23]选取。

图12 疲劳载荷分析过程示意图
表3为应力水平40%条件下,L型胶接试验件疲劳分层数值结果和试验结果对比,误差为2%,表明模型能够准确预测复合材料L型胶接连接件的疲劳寿命。

表3 试验和数值结果对比
图13给出了L型胶接试验件在不同疲劳阶段的分层扩展情况及裂尖应力集中分布,选取L型板和底板的连接区域进行局部放大。可以观察到,疲劳裂纹扩展前,L型板在圆弧过渡区域存在应力集中,Mises应力较大,导致了较高的能量释放率,故首先产生局部分层,随着疲劳损伤的不断累积,分层损伤不断向前扩展,且分层裂纹尖端的应力较高,进一步促进分层损伤的扩展,分层区域迅速贯穿整个搭接区域,胶接接头丧失承载能力并发生疲劳破坏。

图13 不同疲劳阶段分层及裂尖应力集中分布
4 结 论
本文通过试验和数值方法对L型复合材料胶接接头的静力与疲劳分层损伤扩展和失效进行研究,通过系统研究得出以下结论:
1) 静力载荷作用下,由于应力集中,L型接头胶接层开始起裂,之后载荷迅速下降,随着继续加载,分层不断扩展,直至发生大面积分层,试验件丧失承载能力,胶面发生内聚破坏。
2) 疲劳载荷作用下,L型接头胶接层前缘应力集中导致较高的能量释放率,首先发生分层扩展,分层损伤不断向前扩展,且分层裂纹尖端的应力较高,疲劳分层区域迅速贯穿整个胶接区域。
3) 本文建立的复合材料胶接接头的静力和高周疲劳分层本构模型,修正了疲劳分层扩展中能量释放率算法的计算方法,提高其计算精度,可有效预测静力和疲劳加载下胶接结构分层损伤的起始、演化和失效机理。

