Walker星座性能修复构型重构的弹性力学解法

贺波勇, 李恒年, 周庆瑞, 麻蔚然

(1.西安卫星测控中心 宇航动力学国家重点实验室, 陕西 西安 710043;2.西北工业大学 航天学院, 陕西 西安 710072; 3.中国空间技术研究院 钱学森空间技术实验室, 北京 100094)

Walker星座是全球覆盖最有效星座[1]，常用于对地观测、导航和互联网通信等。近年来，随着卫星和运载火箭标准化、商业化和产业化，星座部署成本降低。而全球观测覆盖率、重访时间分辨率等需求增长使得星座中卫星数量急剧增长，如Space-X公司Star-link互联网星座预计最终部署约42 000颗卫星。因单颗卫星系统故障解体或空间碎片撞击引发Kessler效应[2]可能导致Walker星座中同轨道面相邻多颗卫星均处于碎片带，进而产生故障，引起星座整体性能下降[3]。星座性能快速修复有2种途径：①地面具备快速发射响应能力，补充卫星来弥补失效卫星原有职能[4]；②依靠在轨卫星构型重构对星座整体性能进行一定程度修复[5]。前者由于近年来快速响应火箭技术发展逐渐被重视，但快响火箭运载能力和响应周期仍难满足现实需求，而后者因其可快速实现性被学者长期研究。对于卫星数量较少的星座可以采用轨道力学专家知识简单计算出可接受重构策略[5-6]，甚至采用间接法给出最优策略[7]，而对于卫星数量稍多的情况采用智能进化算法[8-10]或拍卖算法[11]给出可行重构策略。一些学者也将多Agent技术引入到卫星编队构型重构问题中来[12]，但重构位置分配问题仍利用拍卖算法求解[13]。随着星座中卫星数量急剧增长，轨道力学专家知识方法难以胜任，基于进化算法或拍卖算法的搜索方式显现出维数灾难问题[14]。

本文试用薄膜弹性力学理论求解Walker星座性能修复构型重构策略。

1 在轨重构问题描述

星座重构一般发生在星座分阶段部署、任务调整重构和卫星故障在轨重构等场景。分阶段部署可以利用发射窗口[15]、升交点进动[16]和大气阻力[17](低轨)等节能方式部署；任务调整重构的典型场景如指定区域详细观测任务，一般利用专家知识[6]或进化算法[8]给出可行解；卫星故障在轨重构任务可以分为单星故障、同轨道面多星故障和多轨道面多星故障3类需要重构的场景，构成多约束多目标优化问题[18]。

1.1 Walker星座及典型故障

Walker星座可用5个参数N,P,F,h,i描述。(N,P,F)为离散正整数,分别为卫星总个数、分布轨道面数和相位因子,0≤F≤P-1。h,i分别为轨道高度和轨道倾角,Walker星座默认所有卫星高度和轨道倾角相同。升交点赤经

Ωi=Ω0+i·ΔΩi=1,…,P-1

(1)

1.1.1 全球覆盖率

全球覆盖率主要由倾角i、轨道高度h和卫星的对地覆盖波束半张角θ决定,如图1所示,全球覆盖率为

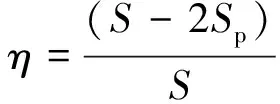
(2)

(3)

(4)

图1 Walker星座对地观测几何

1.1.2 时间分辨率

除对地可见光观测卫星外,Walker星座时间分辨率主要有经度方向和轨道面内2个方向:

(5)

式中，ωe=7.292 115×10-5rad/s为地球自转角速度。

(6)

导致Walker星座中单颗卫星失效的原因可能来自于卫星自身故障或空间碎片小动量碰撞,而同轨道面多星故障可能来自于卫星姿态控制系统失效导致的卫星解体或空间碎片大动量碰撞产生的碎片带(云),这些碎片云会贴近轨道面沿轨道迹向散开,一段时间后散布相位区间增大[19],引起Walker星座单颗、相邻多颗、甚至某个轨道面内所有卫星均失效。

1.2 轨道调整模型

考虑星座重构时为了节约燃料消耗,均采用Gauss摄动方程进行轨道小偏差调整。

1.2.1 相位调整

为保证均匀对地覆盖,Walker星座中卫星均为近圆轨道(e≈0),考虑地球扁率J2=1.083×10-3项影响,忽略高阶项,轨道平相位角速率为

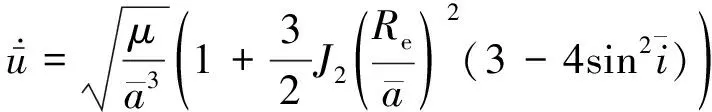
(7)

(8)

(9)

(10)

1.2.2 升交点赤经调整

由Gauss摄动方程知,直接调整升交点赤经燃料消耗代价较大,通常采用半长轴和倾角偏置产生升交点赤经漂移速率差值调整升交点赤经。同样考虑近圆轨道地球扁率影响,平升交点赤经漂移速率为

(11)

(12)

(13)

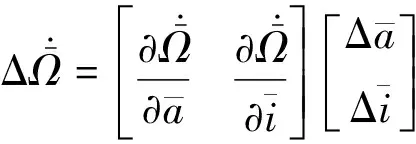
(14)

如果采用切向速度增量Δvt和法向速度增量Δvh在最佳时刻分别调整轨道半长轴和倾角,有

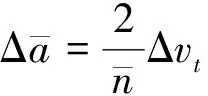
(15)

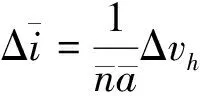
(16)

2 薄膜弹性力学解法

当Walker星座中卫星数量较多时,可以认为所有卫星分布在地心球面或球带面薄膜板上,当某一个或某些轨道平面卫星失效,可以等效为该球膜或球带薄膜产生漏洞,如图2所示。

图2 星座修复重构仿生薄膜弹性力学示意图

星座在轨重构等效为使用外力拉伸漏洞附近薄膜,使之发生薄膜形变位移,来缩小漏洞面积,一定程度上恢复漏洞区域卫星的缺失职能。由于Walker星座卫星轨道调整不会给所在球面或球带面带来轨道高度显著变化,这与薄膜板弹性力学无弯曲应力形变相似。

2.1 仿正交异性薄膜板刚度矩阵

不考虑剪切应变的正交异性薄膜板刚度矩阵如下

(17)

式中:Exx,Eyy分别为局部坐标x,y轴向的等效弹性模量;νxy,νyx分别为x,y轴向的泊松比;柔度矩阵S=D-1,应变与应力关系为ε=Sσ。

(18)

对于限定轨道调整时长t的星座重构任务而言,相位和升交点调整量分别为

(19)

2.2 弹性力学Ritz解法

设星座重构调整总势能函数为

Π=U+W

(20)

式中:U为星座重构轨道机动代价等效函数;W为星座重构前后整体性能指标下降量。

图3 Walker星座重构前后失效区域示意图

(21)

设2个相邻轨道面内相位接近的2sdis卫星分别从左右两侧靠近失效区域调整升交点赤经ΔΩ,则其余轨道面相位接近的卫星向失效区域调整升交点赤经量为

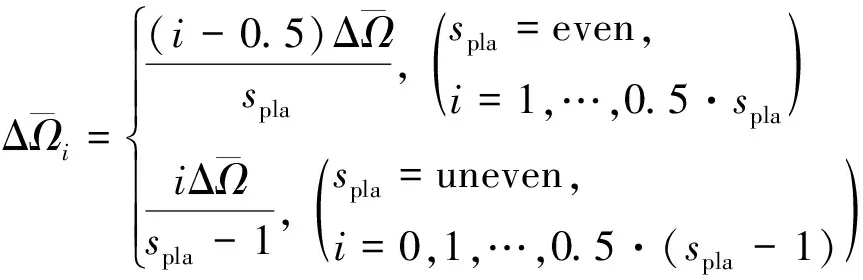
(22)

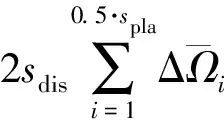
进一步可以通过(18)式和(19)式计算出最佳时刻轨道调整速度增量累加值Δvt和Δvh,则可设轨道机动代价等效函数为

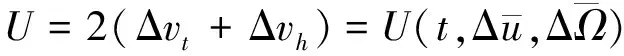
(23)

参考文献[5]中修复比例概念,设星座未受损时时间分辨率为Δtini,Δtini取(5)式和(6)式较大值。受损后星座时间分辨率为

(24)

修复后时间分辨率为

(25)

则可设星座重构前后整体性能指标下降量等效函数为

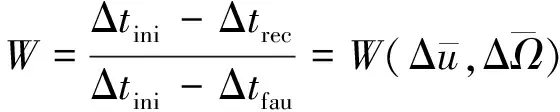
(26)

仿照弹性力学理论中最小势能原理对(20)式求偏导,使偏导数为0。

(27)

(28)

(29)

(30)

星座重构轨道机动代价等效函数U会随容许的轨道调整时长t变化。

3 算 例

3.1 算例1

参考文献[5]中Walker星座[(N/P/F),(h,i)]=[(18/3/2),(1 000 km,30°)],星座未受损时的时间分辨率为48 s,由(6)式可计算地面覆盖角约为28.626°。与文献[5]相同,假设失效卫星为2颗和3颗,按照本文方法计算重构前后性能与文献指标对比如表1所示。

表1 对比文献[5]方法星座重构性能指标

由受损后时间分辨率可知,本文考虑地球扁率的模型更为精确。设置同样的重构时间,相比于文献[5]计算结果,本文重构策略各种性能指标也更优。原因是:利用弹性力学方法,使剩余卫星分别从两侧同时向故障卫星方向实施轨道机动,分摊到每颗卫星的机动能耗和所有机动卫星的总机动能耗均有所减少,这种星座重构策略更接近自然界中材料的弹性力学协调变形行为,但代价是几乎全部剩余卫星都需机动。

3.2 算例2

以新一代铱星星座轨道高度为例[20],假设Walker星座参数[(N/P/F),(h,i)]=[(66/6/？),(774.63 km,86.39°)],赤道连续覆盖Δtini=Δtλ=0,通过(5)式可知单星地面覆盖角d≥30°,取d=30°,假设重构时长为t=86 400 s,则某轨道面内相邻失效卫星数量sdis=1,2,3,…,11时,重构前后性能指标如表2所示。

表2 新一代铱星星座重构性能指标

算例2设置的重构时长为1天,约为算例1的10倍,最大速度增量及速度增量总和显著降低至百米每秒量级,具备工程实施可能。当轨道面失效卫星数接近该轨道面所有卫星数时,即便留100天重构时长用于其余轨道面卫星调整升交点赤经,也需千米每秒量级的变轨速度增量,在轨卫星很难付出这样的代价,建议由地面发射新卫星补充失效卫星原功能。

4 结 论

本文提出利用薄膜板线弹性力学Ritz方法求解Walker星座典型故障场景中,在轨卫星机动重构星座构型的问题。算例表明该方法可以解析求解重构策略,求解的重构策略相比已有文献结果更优更协调。