基于短时心电信号的室颤预测分析

刘健，霍亭，李锦#，凤飞龙，胡静

摘要：心脏猝死中75 %～80 %的初始节律为心室颤动，如果室颤的发生可以采取一定措施提前预测并对患者发出预警，则将大大降低室颤致死率。本文以心电信号的非线性方法中样本熵分析方法和复杂网络的可视图算法来区分正常状态，室颤发生前20分钟和室颤的各个不同状态，可以很好的区分三者的状态，为实时监控心脏猝死情况提供一定的理论支撑。

关键词：室颤预测，样本熵，复杂网络，心电信号

研究表明，对猝死患者的人来说，提前20 min的预测可以挽救一个人的生命。2011年，研究学者通过构建复杂网络来区分室颤各种不同状态[1]。同年，董昭通过复杂网络区分癫痫患者并预测取得良好的效果[2]。2014年，利用有向网络区分不同疾病的3种情况[3]。2016年，杨帆等人同样用非线性方法区分出来猝死患者[4]，Liu等人[5]应用了脑电信号，而不是心电信号进行了室颤的有效区分;刘海龙等人[6]对心电信号当中的心脏猝死前兆室颤进行详细的区分，心电信号的复杂性使得任何一种方法都不能很好的区分心电信号不同状态，本文结合样本熵和可视图分析室颤不同状态，室颤的到来，样本熵值的值有显著性下降，表明室颤为心脏系统的心血管带来致命的缺陷。健康人的心电信号度分布熵值最大，室颤状态的最低，由此可知度分布熵值是随着室颤状态的到来而逐渐降低，室颤并不是瞬间就发生的，而是有一定的时间来预测发生，两者得到一致的结果为将来的临床实验提供了一定的理论依据。

1 方法

1.1 样本熵

样本熵作为一种改进算法，它不太依赖时间序列长度。算法表述如下。

（1） 定义算法相关参数m、r，其中，m为整数，表示比较向量的长度;r为实数，表示“相似度”的度量值。

（2） 定义向量与之间的距离为两向量对应元素中差值最大的一个，即：d[X（i） ，X（j） ] = maxk = 0～m-1|u（i+k） -u（j+k） |，j的取值范围为[1，N-m+1]，X（i） ≠X（j） 。

（3） 把维数加1，令k = m+1，重复步骤3～4，XK（i） 与XK（j） 的距离小于r的个数： Ak（r） = （N-k+1） -1∑i = 1（N-k+1） Aik（r） 。所以，Bm（r） 是在容限r以内新构造序列匹配m个点的概率，Ak（r） 是匹配m+1个点的概率。

（4） 则样本熵定义为  SampEn = limN→∞     {-ln[Ak（r） /Bm（r） ]}

1.2  可视图算法

可视图算法由Lacasa等人提出[3]，在可视图中，图中的每个节点代表时间序列的时间样本，并且两个节点之间的边表示相应的时间样本可以彼此查看，将时间序列X映射到其可视图来进行研究。

度分布熵在文中表示为EDD，用于量化度分布的形状，公式：EDD = -∑i = 0Max（k）   p（k） ×log p（k） 其中p（k） 定义为图中度为k的节点的分数，max（k） 为k的最大值。.

2 ECG信号的非线性分析

2.1 实验数据

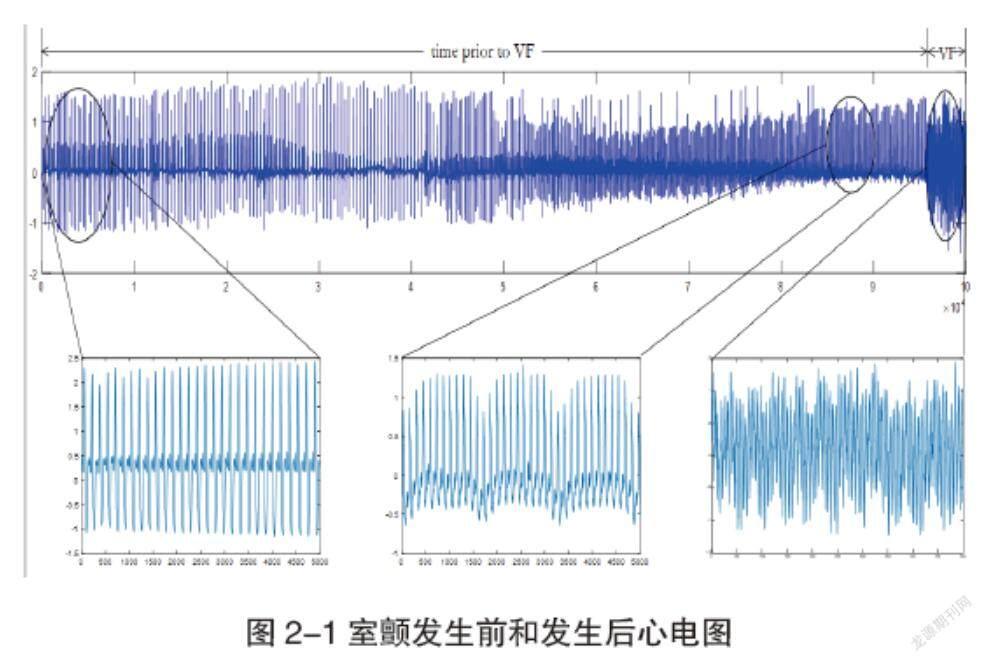
本章采用的数据来自公开数据库Physionet CUDB-ECG数据库Physionet SDDB-ECG和Physionet NSRDB-ECG。該数据库总共由40条记录单元组成，每组1分钟15 000点数据，首次室颤前的心电数据各分钟和发生室颤后一分钟的数据，从图中可以看出，室颤和发生室颤前几分钟的信号形态明显不同，因此构造出的样本熵和复杂网络也不相同，从而借助样本熵和复杂网络可视图特性对发生室颤前的信号进行分析、识别。

2.2 样本熵分析结果

样本熵计算所需要的数据长度一般是1000点左右[6]，因此，本小节实验在健康人、室颤前20 min状态、室颤状态组选取连续每分钟15000点，可以满足实验数据需求并达到有效的结果，然后计算粗粒化后样本熵。

图2-2是健康人、室颤前20 min状态、室颤状态组的样本熵箱线图。从临床医疗数据统计来说，ECG信号熵值随着人体心脏健康状态的变化而呈现逐渐下降的趋势[7]。从图3-2中可以看出，在室颤前20 min内，各组数据的熵值较为接近，但是随着室颤的到来，熵值的差距变大。在不同状态下，健康人的样本熵均值最大，室颤前状态次之，室颤患者的均值最小。这表明健康人的复杂度最高即相较于室颤患者，健康人的ECG信号拥有较复杂的结构。室颤患者的复杂度低于正常人，从生理医学角度解释可能是因为室颤患者潜在的心血管疾病危险因素对心脏系统产生了较大的负面影响，严重影响了心脏系统的稳定性，使得心电信号复杂度降低。

3 可视图算法结果

健康人的复杂网络度分布熵（EDD） 分析指标均值最大，室颤前20 min状态次之，室颤状态最低，表明健康人心脏系统非线性耦合性最强，而室颤状态对于人体这一机能产生了负面影响度分布熵（EDD） 指标和样本熵对于区分室颤和正常状态具有统计学上的显著差异，且实验结果都表明度分布熵（EDD） 的差异性更显著，呼应了侯凤贞等提出的EDD有望成为揭示心血管系统的动力学标记这一观点[8]。

4 总结

近几年来，心电信号的非线性分析逐步发展成为主要的研究发展趋势，本文认为将时间序列传统的非线性分析方法和复杂网络结合起来共同研究，不仅能更加深入地认识复杂系统，从而提供更多的解决问题的新思路，还可以为数据的分析提供双重检查保障，使得结果更加准确。这种分析模式不仅可以推广到其他信号的分析处理中，还可以用于更多的疾病诊断中。

参考文献

[1]Paolo Melillo，Raffaele Izzo，Ada Orrico，et al.Automatic Prediction of Cardiovascular and Cerebrovascular Events Using Heart Rate Variability Analysis[J].PloS one，2015，10（3）：e0118504.

[2]董昭通，李小勇.面向大数据的分布式缓存设计[J].通信技术，2020，53（1）：6..

[3]Costa M，Goldberger A. L，Peng C.K.Multiscale entropy analysis of complex physiologic time series[J].Physical Review Letters，2002，89（6）：068102.

[4]杨帆，黎宁，刘恩.非线性最小二乘法及BP神经网络在血管外给药动力学模拟中的应用[J].数理医药学杂志，2007，20（2）：200-202.

[5]Kamath，Chandrakar. Assessment of heart rate dynamic characteristics during meditation using symbolic dynamics analysis[J].Frontiers in physiology，2016，7（44）.077441.

[6]刘海龙，唐奇伶.基于径向基函数神经网络的心电图ST段形态识别[J].生物物理学报，2005，21（6）：7.

[7]王俊，宁新宝，马千里.基于多尺度熵的心电图分析[J].中国生物医学工程学报，2008，27（3）：331-334.

[8]侯凤贞，武小川.基于极短时心率变异性分析的充血性心力衰竭诊断可行性探讨[J].生物医学工程杂志，2016，33（3）：559-563.