基于模糊迭代学习控制的机器人轨迹跟踪
袁海国 秦光耀 王鹏宇


摘 要:针对机器人的强耦合性、非线性、时变性等难以控制的特点,本文提出模糊迭代学习的控制策略,对机器人关节和转角进行跟踪控制,并且将跟踪控制结果与迭代学习控制进行对比。仿真结果显示,在相同迭代学习次数下,模糊迭代学习控制能够更好地跟踪预定轨迹,具有良好的控制性能。
关键词:非线性;迭代学习;路径跟踪
中图分类号:TP391.9文献标识码:A文章编号:1003-5168(2021)03-0031-03
Robot Trajectory Tracking Based on Fuzzy Iterative Learning Control
YUAN Haiguo QIN Guangyao WANG Pengyu
(Zhengzhou Electric Power College,Zhengzhou Henan 450000)
Abstract: Aiming at the robot's strong coupling, nonlinearity and time-varying characteristics, which were difficult to control, this paper proposed a fuzzy iterative learning control strategy to track the robot joints and corners, and compared the tracking control results with iterative learning control. The simulation results show that under the same iterative learning times, fuzzy iterative learning control can better track the predetermined trajectory and has good control performance.
Keywords: nonlinear;iterative learning;path tracking
機器人在工业、农业等重复性劳动领域的应用越来越广泛,随着智能工业的发展,人们对机器人的轨迹跟踪和控制要求越来越高[1]。机器人关节位置和转角位置的跟踪与控制是许多学者面临的难题,由于其非线性、强耦合性特点,传统的控制方法如PID控制、模糊控制、神经网络控制等难以有效地发挥控制作用。朱欣华等人提出位置约束的控制方法,在给定的期望路径附近建立矢量场并且引入位置约束[2]。蒋建东等结合模糊控制,提出自适应前视距离自主跟踪控制算法,在纯追踪算法中对前视距离参数进行动态调节[3]。陈壮等人针对不确定环境下的不稳定性,建立机器人空间运动模型,进而对其进行控制[4],但控制精度并没有达到理想预期。
迭代学习控制是自动控制技术和人工智能相结合的一种新型控制技术,它的记忆和学习功能促使其成为智能控制领域中新的研究和发展方向[5];它适用于具有重复运动特点的被控系统,其目标是达到有限时间或区间上的高精度跟踪,通过将系统输出的轨迹与给定的期望轨迹比较,根据两者的偏差来对不理想的信号进行修正,进而产生更加精准的控制信号来提高系统的跟踪性能。迭代学习控制在使用时无须考虑被控对象数学模型的准确度,因此对于建模不良系统的控制更具有现实意义,十分适合机器人等强耦合、非线性、时变性系统的控制[6]。
为对机器人进行高精度控制,针对机器人系统的非线性、强耦合性,本研究将模糊控制和迭代学习控制相结合,设计模糊迭代学习控制器来控制机器人,抑制外界因素影响,使其沿预定轨迹进行运动。
1 控制方法分析
1.1 迭代学习控制原理
当机器人做重复运输的运动时,其状态空间方程如下:
[xk(t)=Axk(t)+Buk(t)yk(t)=Cxk(t)] (1)
式中,[k]为机器人运行次数;[xk(t)=Axk(t)+Buk(t)]为机器人状态方程;[yk(t)=Cxk(t)]为机器人输出方程;[A]为系统矩阵;[B]为控制矩阵;[C]为观测矩阵;[u]为控制作用;[x]为状态向量;[y]为系统输出。
在实际运行中,式(1)系统满足下列要求:系统的期望轨迹[yd(t)]是已知的并且能够达到;系统在每次运行时的期望初态和运行初态是不变的、相等的,即满足[xd(0)]不变,且[xk(0)=xd(0)]。
在每次运行时,机器人轨迹都是已知的且可达到的,同时机器人的初始位置和最终位置不变,本文研究同一重复运动状态下的机器人情况。其间利用[uk+1,1],[uk+1,2],…,[uk+1,i-1]分量来代替[uk,1],[uk,2],…,[uk,i-1]分量,学习律为:
[uk+1(t)=uk(t)+LPek(t)+LDek(t)] (2)
式中,[ek(t)=yd(t)-yk(t)];[k]为迭代次数,即机器人运行次数;[LP]、[LD]为增益矩阵。
由此可见,迭代学习控制中的参数是不变化的,目前需要寻找一种方法来对式(2)中的参数进行校正,进而实现一种动态的自学习过程,提高控制对象的精度和收敛速度。
1.2 模糊迭代学习控制方法
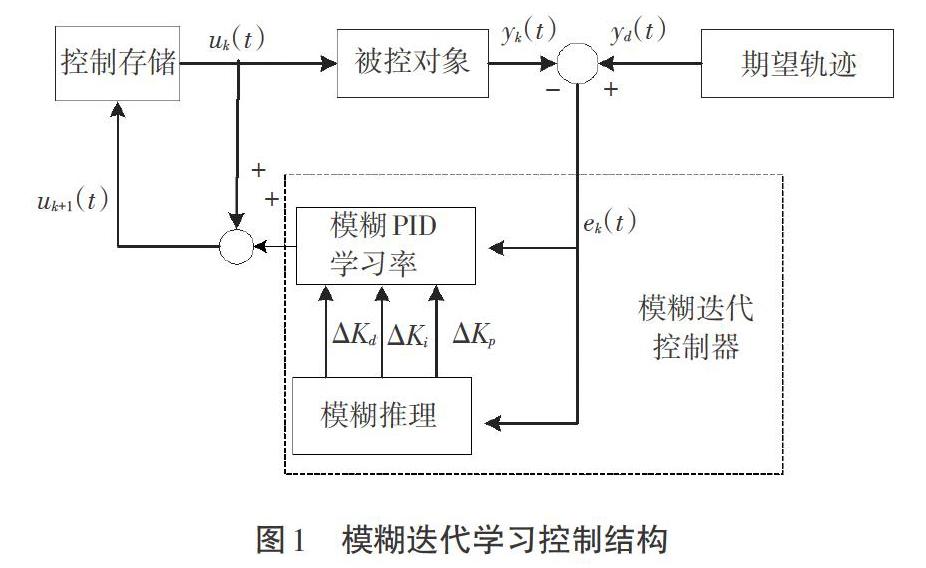
模糊迭代学习控制结构如图1所示,其采用闭环控制系统,将传统的PID参数作为参考,通过模糊整定单元对PID参数进行实时调节,从而生成精度更加准确的模糊PID控制学习率,更加具有抗干扰能力。
模糊控制利用仿人模糊推理,可以在控制系统中取得良好的控制效果,核心是模糊控制器。控制器的输入量一般是系统误差或系统误差变化率。对于精确的输入量,要进行线性或非线性变换,同时,要寻找合适的隶属函数来进行确定。模糊规则的建立是模糊控制器设计的重中之重,关系到控制效果和控制性能。
在对控制器进行设计时,出于对控制精度和控制算法复杂程度的综合考虑,将输入、输出的语言值分成七个模糊子集,即“负大(NB)”“负中(NM)”“负小(NS)”“零(ZO)”“正小(PS)”“正中(PM)”“正大(PB)”。模糊输出变量采用运算简洁而快速的三角隶属函数,隶属函数图如图2所示。
在设计机器人模糊控制器时,需要对模糊控制的过程进行优化,包括机器人实际关节位置与期望关节位置之间的偏差[e]以及偏差变化率[ec]。經过理论分析和实际检验,可以归纳出偏差[e]和偏差变化率[ec]与模糊输出变量[ΔKp]、[ΔKi]和[ΔKd]之间的关系[7-8]。
如果[e]比较大,[ΔKp]应取较大的值,这样会加快系统的响应速度,减小系统的时间常数和阻尼系数;但是,[ΔKp]不应过大,过大会使系统失去稳定,在开始时刻,[ΔKd]取小一些,一般限制[ΔKi],有时[ΔKi]甚至为零。
如果[e]处于中等状态,[ΔKp]应取小一些,这样使系统的超调小一些,此时[ΔKd]的选取尤为关键,要恰当地选择[ΔKd],也可适当增加[ΔKi],但不应过大。
如果[e]较小,[ΔKp]取值应小一些,[ΔKi]应取较大些,这样被控系统才有更好的稳态性能,同时考虑到系统的鲁棒性(抗干扰性),防止其在平衡点震荡,若[ec]较小,[ΔKd]应大些,当[ec]较大时,[ΔKd]取小一些。
模糊控制查存表可以反映偏差[e]和偏差变化率[ec]与输出量[ΔKp]、[ΔKi]和[ΔKd]之间的关系,无论采用何种去模糊方法,计算所得的值应为模糊论域中的元素,若采用去模糊方法所计算的结果不是输出的模糊论域中的元素,则应对该控制的输出进行必要处理。模糊迭代学习控制算法控制流程如图3所示。
模糊迭代学习算法流程如下:[k=0],对被控对象机器人进行初始状态的设置,给出机器人的期望运行轨迹[yd(t)],并对其进行存储;依据给定的期望轨迹设置机器人的控制输入[uk(t)],并将其施加于机器人系统,得到机器人的控制输出[yk(t)];本次模糊控制学习之后,计算本次的机器人运行误差[ek(t)=yd(t)-yk(t)],将误差[ek(t)]与[uk(t)]存储并带入控制律得到下次的控制输入;检验误差[ek(t)]能否达到迭代结束要求,若[yd(t)-yk(t)<ε],则结束模糊迭代,若达不到结束要求,则[k=k+1],并跳转到步骤二继续进行模糊迭代运行,直到达到停止要求。
2 仿真结果
由拉格朗日定理可以推出[9],典型的机器人的动力学模型为:
[Iθ+dθ+mglcosθ=τ] (3)
式中,[θ]为机械臂的转角;[d]为摩擦系数;[m]为质量;[g]为重力系数;[l]为转动中心距离;[I]为转动惯量,[I=43ml2];[τ]为关节力矩。
机器人参数为:[m]=1 kg,[l]=0.3 m,[d]=3,g=9.8 m/s2,学习周期为[T]=25 s,[LP=1.02],[LD=1.6]。
设置机器人关节初始状态,并将模糊迭代次数依次增加,分别设置成10、15和30,按照模糊迭代流程进行控制,仿真结果如图4所示,当迭代次数为10时,机器人转角最大误差为0.047°,当迭代次数为15时,最大转角误差为0.042°。当迭代次数较少时,转角与理想转角之间还有误差。随着迭代学习次数的不断增加,机器人的关节越来越靠近预期轨迹,实际转角误差越来越小,当迭代次数[k=30]时,最大转角误差仅为0.037°。
为了验证模糊迭代学习控制方法的优越性,下面结合关节位置仿真,对模糊迭代控制与迭代学习控制进行了对比,如图5所示。当迭代次数[k=1]时,模糊迭代控制与迭代学习控制的最大误差相同,但随着迭代次数的增加,在相同次数的迭代学习下,模糊迭代学习控制最大误差比迭代学习控制误差小,即模糊迭代学习能够更好地跟踪预定轨迹。模糊迭代学习控制收敛速度快,在[k=7]时,关节位置已经得到无误差跟踪。
3 结论
针对机器人强耦合性、非线性等难以控制的特点,本文设计模糊迭代学习控制方法来对机器人关节和转角进行跟踪控制,将跟踪结果与迭代学习控制进行对比。在相同次数的迭代学习下,模糊迭代学习控制最大误差比迭代学习控制误差小,即模糊迭代学习能够更好地跟踪预定轨迹,具有更好的控制性能。
参考文献:
[1]吴锦辉,陶友瑞.工业机器人定位精度可靠性研究现状综述[J].中国机械工程,2020(18):2180-2188.
[2]朱欣华,王健,郭民环,等.基于位置约束的两轮驱动机器人路径跟踪控制方法[J].中国惯性技术学报,2018(5):680-685.
[3]蒋建东,张钧,李聪聪,等.履带式移动机器人自主跟随算法研究[J].浙江工业大学学报,2017(4):355-360.
[4]陈壮,王宪伦,陈闪.基于优化ADRC的单臂机器人轨迹跟踪研究[J].机械与电子,2020(10):77-80.
[5]AHN H S,CHOI C H,KIM K B.Iterative learning control for a class of nonlinear systems[J].Automatica,1993(6):1575-1578.
[6]李仁俊,韩正之.迭代学习控制综述[J].控制与决策,2005(9):961-966.
[7]乔志杰,王维庆.模糊自适应控制器的设计及其仿真[J].自动化与仪表,2008(1):26-29.
[8]王伟,叶真,李瑞杰.在线参数自整定模糊PID控制器的设计与仿真[J].安徽师范大学学报(自然科学版),2013(2):133-136.
[9]刘志学,吴丽娟.模糊迭代学习在单关节机器人运动控制中的应用[J].辽宁科技大学学报,2009(4):378-382.

