变阶次分数阶梯度下降法的研究
李佳维,申永军,杨绍普
(1.石家庄铁道大学 交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043;2.石家庄铁道大学 机械工程学院,石家庄 050043)
从分数阶微积分提出至今已有三百多年的历史。在很长一段时间里,由于缺乏相应的物理背景,它一直被当做一种数学的纯理论研究。随着科学技术的发展,研究人员渐渐意识到分数阶微积分对于解决相关的实际问题,是一种高效且精确的数学工具。目前,分数阶微积分被广泛地应用于很多领域,如自动控制[1-2]和系统识别[3-4]等。
梯度下降法是在待求极值点的目标函数为凸函数的情况下最基础的优化方法[5],广泛应用于系统辨识[6-7]、图像处理[8-9]、自适应滤波[10-11]等方面。虽然分数阶微积分与梯度下降法在各自的领域已经得到了广泛的应用,但是将两者结合的研究刚刚起步。Pu等[12]首次提出针对二元函数的分数阶梯度下降法,该方法严格按照分数阶微积分来定义,但是得到的极值点并非目标函数实际的极值点,而是在实际极值点的附近。Chen等[13]研究了分数阶梯度下降法中的分数阶微分下限随迭代过程变化的情况,并且通过高阶截断,进一步简化了分数阶梯度下降法。卫一恒提出针对不改变分数阶微分下限的变阶次分数阶梯度下降法,保证了在微分下限不变的情况下,分数阶梯度下降法依然可以收敛至真正的目标函数极值点。程松松[14]针对分数阶LMS自适应滤波算法,提出迭代阶次混合切换机制,明显提高了滤波算法的性能。李大字等[15]构造了一种基于分数阶梯度下降法的模型预测控制器。由于分数阶微积分所特有的良好性质,分数阶梯度下降法已经在LMS滤波[16]、系统辨识[17-18]等方面得到了应用。
为了进一步优化分数阶梯度下降法的性能,解决迭代过程中收敛速度与收敛精度之间的矛盾,本文在前述研究的基础上,提出了三种不同的分数阶阶次设置方法,旨在得到更好的寻优结果。
1 梯度下降法和分数阶微分
1.1 梯度下降法
梯度下降法是求解无约束优化问题最常用的方法之一,它是利用一阶梯度求解目标函数极小值的算法。假设目标函数为f(x),则梯度下降法的迭代过程为
xk+1=xk-μ·∇f(xk) (k=0,1,2,…)
(1)
式中:x(k)表示当前的自变量值;x(k+1)表示待求的下一个位置;μ代表学习率,它决定了自变量移动到最优值的速度快慢;∇f(xk)是当前位置的一阶梯度。当目标函数梯度的绝对值小于某一预设的极小正数时,迭代停止,此时的x(k)为求得的优化结果。
1.2 分数阶微积分
Caputo分数阶微分定义为
(2)
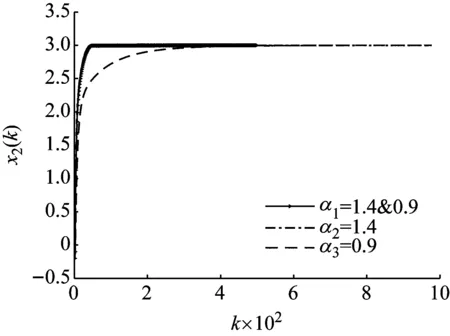
式中:c和x代表微分的上下限,且c通常取0或者-∞;α代表微分的阶次,n-1<α (3) 对式(2)进行泰勒级数展开[19-20],得到 (4) 将式(1)中的一阶梯度替换为分数阶梯度,可得分数阶梯度下降法的迭代算法 xk+1=xk-μ·∇αf(x) (5) 为方便分析分数阶梯度下降法(fractional-order gradient descent method,FOGDM)的性质,将式(4)代入式(5)中,得 (6) 以一般的一元二次函数f(x)=ax2+bx+g为例,利用分数阶梯度下降法求该函数的极值点x*。取泰勒级数的前两项,具体迭代算法为 (7) 当a=1,b=-12,g=36时,f(x)=x2-12x+36,f(1)(x)=2(x-6),f(2)(x)=2,代入式(7),得 (8) 给定c=0,x0=-1,μ=0.1,并且设置分数阶阶次依次为α1=1,α2=0.7,α3=1.5,从而得到迭代结果如图1所示。从图中可见常规梯度下降法可以保证系统收敛至目标函数实际极值点,而原始的分数阶梯度下降法则不能,原因在于它的迭代终止条件 图1 分数阶梯度下降法与常规梯度下降法迭代过程曲线Fig.1 Iteration process curves of fractional-order and conventional gradient descent methods (9) 不仅与x有关,而且与微分下限c和微分阶次α都有关系。 将式(6)中的微分下限由固定点c替换为x(k-1),使得微分下限随迭代过程变化,得到 (10) 在梯度下降法的迭代过程中,迭代点将很快满足|xk-xk-1|<1。当分数阶阶次α范围在(0,1)时,在式(10)中,保留右侧级数第一项。此时,简化的分数阶梯度下降法为 (11) 将常数Γ(2-α)与μ合并,同时仍用μ表示。为了与常规梯度下降法保持一致,将导数中的x(k-1)用x(k)替换,得 xk+1=xk-μ·f(1)(xk)·(xk-xk-1)1-α (12) (13) 显然α=1时上式退化为常规的梯度下降法。进一步研究发现式(13)也适用于α∈(1,2)的情况,因此上式算法适用于分数阶阶次α∈(0,2)的情况。如果算法收敛,那么,一定收敛至目标函数真实的极值点。 假设目标函数仍为f(x)=x2-12x+36,已知真实极值点为x*=6,利用式(13)求解目标函数极小值点。不同分数阶阶次依次设置为:α1=0.7,α2=0.9,α3=1.0,α4=1.4,α5=1.7,图2给出了不同阶次分数阶梯度下降法的迭代过程对比结果。由图可知,在系统稳定的前提下,当阶次α∈(0,1)时,分数阶梯度下降法保证系统渐进稳定地收敛至目标函数极值点;当阶次α∈(1,2)时,分数阶梯度下降法使得系统有超调地收敛至目标函数极值点。 图2 不同阶次分数阶梯度下降法的迭代过程曲线Fig.2 Iteration process curves of fractional-order gradient descent methods with different orders 利用分数阶梯度下降法求解目标函数极值点的过程中,阶次不同将会导致不同的收敛速度和收敛精度。为了解决二者之间的矛盾,本文提出了三种改进的变阶次分数阶梯度下降法。 第一种是连续变阶次分数阶梯度下降法,其中设计变阶次的形式为 (14) 式中,δ为一正值。在迭代初始位置,由于x(k)与x(k-1)差别较大,此时分数阶阶次值较高,相较于整数阶梯度下降法,有更快的收敛速度,随着迭代过程的进行,当|xk-xk-1|→0时,α(xk)→1.1,此时分数阶梯度下降法转化为常规梯度下降法,使得变阶次梯度下降法具有与常规梯度下降法相近的收敛精度。 因此,利用上述形式的α(xk),分数阶梯度下降法可以获得与高阶相近的收敛速度,又可以保持与常规梯度下降法相近的收敛精度。 在分数阶梯度下降法的迭代过程中,高阶次(1<α<2)可以获得比常规梯度下降法快的收敛速度,但是它的收敛精度相较于常规梯度下降法有一定程度的下降;低阶次(0<α<1)可以获得比常规梯度下降法更高的收敛精度,但是收敛速度相较于常规梯度下降法大幅减慢。 由此分析可知,如果在迭代的起始位置利用高阶次梯度下降法,随着迭代过程的进行,当目标函数梯度的绝对值小于某一预设的正值时,切换至低阶次梯度下降法,整个迭代过程就可以获得与高阶次相近的收敛速度、与低阶次相近的收敛精度,从而可以解决迭代过程中收敛速度与收敛精度不可兼得的矛盾。 在混合阶次切换的分数阶梯度下降法迭代过程中,初始迭代的高阶次可以显著提高迭代算法的收敛速度;当目标函数梯度绝对值下降至某一预设值,如果为了提高收敛精度而选择一固定的低阶次α,又会使迭代过程忽然变得很慢。由于与极值点收敛精度相关性最大的是接近极值点时刻的分数阶阶次,因此当目标函数梯度绝对值下降至某一预设值,将定阶的高阶次切换为一个减函数形式的低阶次,则既可以保证迭代速度不至于忽然变得很慢,又可以保证算法的收敛精度。 低阶阶段的减函数形式可选为 (15) 式中:δ为一正值;β∈(0,1)。 在这一部分,我们选取Booth函数作为典型算例,来验证本文提出的三种变阶次方法对于分数阶梯度下降法收敛能力的改进效果。其中Booth函数表达式为 f(x1,x2)=(x1+2x2-7)2+(2x1+x2-5)2 (16) 利用连续变阶次的分数阶梯度下降法求Booth函数极小值点。选取δ=0.15,变阶次设置为 (17) 分数阶阶次依次设置为α1=α(xk),α2=1,α3=1.4。 图3和4分别给出了x1和x2的三种不同阶次的分数阶梯度下降法的迭代过程曲线。相较于常规梯度下降法,收敛速度得到了提高,并且由于变阶次函数α(x)在|xk-xk-1|→0时,α(xk)→1,最终可以获得与整数阶相似的收敛精度。 图3 x1迭代过程曲线Fig.3 Iteration curves of x1 图4 x2迭代过程曲线Fig.4 Iteration curves of x2 设高阶次α=1.4,低阶次α=0.9,高低阶次切换的临界条件是|f(1)(xk)|=0.000 02,为对比不同阶次的迭代结果,分数阶阶次依次设置为:α=1.4 &0.9,α2=1.4,α3=0.9。 图5和6分别给出了x1和x2的三种不同阶次的分数阶梯度下降法的迭代过程曲线。从图中可见,利用混合阶次切换的方法,同样可以解决梯度下降法收敛速度与收敛精度不可兼得的矛盾。 图5 x1迭代过程曲线Fig.5 Iteration curves of x1 设高阶α=1.4,当目标函数梯度的范数小于0.000 02时,选取δ=0.15,β=0.9,分数阶梯度下降法的阶次切换成已知α(xk)减函数,且α(xk)∈(0.9,1)。为对比迭代结果,分数阶阶次依次设置为:α1=1.4&α(xk),α2=1.4,α3=0.9。 图6 x2迭代过程曲线Fig.6 Iteration curves of x2 (18) 图7和8分别给出了x1和x2的三种不同阶次的分数阶梯度下降法的迭代过程曲线。结果验证了本文方法的合理性,同样可以解决在梯度下降法的迭代过程中,收敛速度与收敛精度不可兼得的矛盾,获得良好的收敛结果。 图7 x1迭代过程曲线Fig.7 Iteration curves of x1 本文首先介绍了分数阶梯度下降法,揭示了高阶梯度下降法(1<α<2)具有较快收敛速度和低阶梯度下降法(0<α<1)具有较高收敛精度的特性,以及分数阶梯度下降法在收敛速度与收敛精度两者之间无法兼得的矛盾。在此基础上,为结合高、低阶各自良好的特性,提出三种变阶次梯度下降法:连续变阶次的梯度下降法、混合定阶次切换的梯度下降法和高阶定阶低阶变阶的梯度下降法。其中,高阶定阶低阶变阶是对混合定阶次切换方法的延伸。针对不同的目标函数和迭代要求,可以在三种变阶方法中选取最合适的一种,提高参数优化的收敛速度与收敛精度,从而为工程系统服务。 图8 x2迭代过程曲线Fig.8 Iteration curves of x2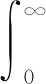
2 分数阶梯度下降法
2.1 原始的分数阶梯度下降法

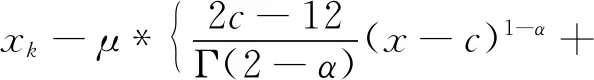

2.2 改进的分数阶梯度下降法
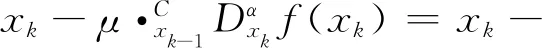


2.3 算法阶次与收敛速度、收敛精度的关系


3 变阶次分数阶梯度下降法
3.1 连续变阶次的分数阶梯度下降法
3.2 混合阶次切换的分数阶梯度下降法
3.3 高阶定阶次低阶变阶次的混合分数阶梯度下降法
4 仿真实验
4.1 连续变阶次的分数阶梯度下降法的仿真


4.2 混合阶次切换的分数阶梯度下降法的仿真
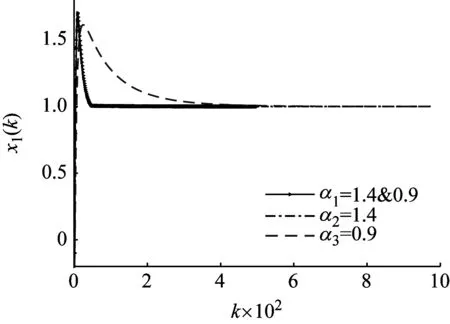
4.3 高阶定阶次低阶变阶次的混合分数阶梯度下降法的仿真

5 结 论


