风电机组风轮表面气流摩擦阻力特性研究

张照煌，黄东权，BUSHRA Tabassum

（华北电力大学 能源动力与机械工程学院，北京 102206）

1 研究背景

风电是可再生的清洁能源，是未来电网中的重要能源组成［2］。风轮是风电机组的核心部件，设计出具有良好气动性能的叶片是提升风电机组能量转化效率的一个重要方法。风电叶片的气动外形设计中应用最多的是动量叶素理论。但动量叶素理论存在自身的不足，Schmitz、Glauert和Wilson等以动量叶素理论为基础，先后建立了计算精度较高的两种方法，即Glauert理论和Wilson理论。其中Glauert理论考虑了风轮的后涡流流动，引入了轴向和周向诱导因子，Wilson理论在Glauert理论的基础上不仅将叶梢损失和翼型的升阻比对叶片气动性能的影响，还将风轮在非设计工况下的性能也考虑在内，Wilson理论以额定风速下风能利用系数最大为优化目标，因此Wilson理论比Glauert理论得到的结果更加准确和全面。

但不管是Glauert理论还是Wilson理论，在设计中都没有考虑气流摩擦阻力的影响。风电叶片在旋转过程中会产生摩擦损耗，量化摩擦损耗可为叶片设计以及减阻提供重要依据。目前测量技术包括直接测量法和间接测量法［3］。直接测量法有摩阻天平、位移差动传感器等，间接测量法是近几年来出现的新技术，如剪切力敏感液晶（Shear Sensitive Liquid Crystal，SSLC）技术［4］、表面剪切敏感膜（Surface Stress Sensitive Film，S3F）技术［5］和荧光油膜技术［6］，这些方法理论上可以获取全局表面摩擦力场，但在仪器安装上有较大难度，得到的结果也有很大的误差。有不少学者通过数值计算的方法对叶片的表面摩擦因素进行研究，并取得初步的成果［7-8］，但这些研究仅是通过实验和数值模拟的方法对特定点的压力数据进行比较验证，没有获得叶片全表面摩擦力的数据。在摩擦理论方面，李宁等利用傅里叶伪谱及并行的方法，模拟不可压平板边界层的转捩过程［9］。蔡小舒等提出了具有拉格朗日性质的运动单帧长曝光图像法（MSFLE），对平板湍流边界层涡结构进行实验测量，并初步进行了分析［10］。宋娟娟等从平板减阻进行研究，对光滑与非光滑平板的阻力进行数值计算，对风电机组叶片专用翼型进行了减阻尝试［11］。Ferrante等［12］研究气泡减阻在平板湍流边界层中的物理机制，分析了湍流边界层的流动机理。Stefes等［13］采用油膜干涉法，使用普雷斯通管和壁面热探针对表面摩擦进行了测量。Muhammad等［14］推导了环状流动空气流过风轮时的力矩表达式。

因此，摩擦力对叶片出力的影响需要从摩擦理论着手，本文应用黏性流体边界层理论［15］，将叶片分为迎风面和背风面，分析叶素上的流动状态，得到摩擦力的计算式，基于文献［1］中叶片桨距角和弦长设计理论，得到了更准确地考虑摩擦力和符合实际工况的弦长。

2 风轮表面气流摩擦力阻力计算

2.1 叶片摩擦力计算模型 要计算叶片旋转的摩擦力，可把叶片沿径向分成无数个微段，每个微段称为叶素，分别计算每个微段的摩擦力再沿着径向积分求出总的摩擦力。但这种方法可行的前提是获得翼型曲线的方程，且知道速度在翼型上每个点的速度分布表达式，但要实现这两点目前还有一定困难。究其原因是目前没有建立翼型方程与其气动性能的联系，在不断变化的流速、变桨、偏航等的影响下还难以获得气流在翼型曲线上各点的速度，求得表达式。在流动空气与叶片相互作用规律的认识及以这种认识为基础的风电叶片翼型理论尚须进行更深入的研究工作［16］。故本模型对翼型作简化处理，首先取某个半径处的叶素为研究对象，将叶素简化为具有弦长和桨距角的平板，分析来流绕过翼型平板的摩擦力。在叶片桨距角设计理论的基础上考虑叶片表面摩擦力对叶片设计的影响。在摩擦力计算模型中，取叶片某半径r处的叶素为对象，如图1所示，将该叶素看作平板，即不考虑翼型形状对叶片气动性能的影响，并按照空气与翼型的作用关系将翼型分为迎风面和背风面，分别研究迎风面和背风面上的摩擦阻力，并根据黏性流体边界层理论计算空气对叶片的摩擦力矩。

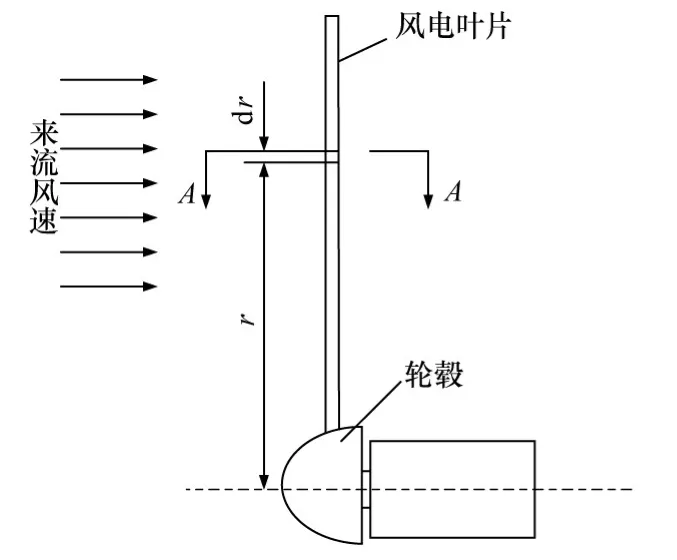
图1 风电叶片及其轮毂位置关系

对来流的几点假设：（1）空气在风轮各处的密度都是定值，（2）各叶素处的空气均为二维流动，各叶素之间没有径向流动、互不影响，（3）不考虑翼型前缘对来流的作用。

来流与平板翼型相互作用关系如图2所示，定义风轮上游来流速度为v∞，翼型攻角为α，桨距角为β，方向与风轮垂直，风轮自身旋转角速度为Ω，l（r）为叶素弦长。

图2 距离轮毂轴心r处叶片桨距角、攻角及弦长

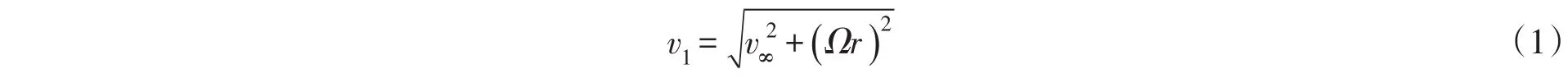
则与平板平行方向上的速度为：

v=v1cosα

空气对平板翼型的摩擦力合力F的方向平行于平板，得到摩擦力F后将其投影到风轮旋转平面上即可得到空气对风轮旋转造成的摩擦阻力。

2.2 平板边界层摩擦力计算 空气黏性很小，黏性对流动的影响实际上仅局限于贴近固体表面的一薄层，这个薄层被称为边界层，如图3所示。沿平板法向方向分布的流速U达到0.99U时的y值为边界层的外边界，δ为边界层厚度。

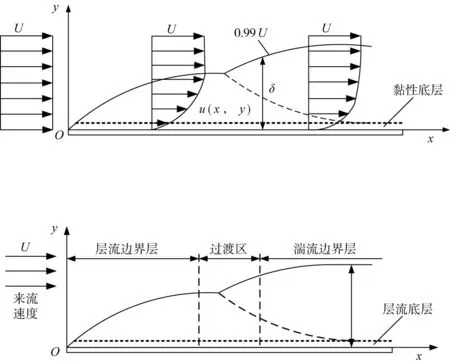
图3 平板壁面绕流边界层

由于流体黏附在平板表面上，速度从零沿薄层横向迅速增至外流速度U，显然边界层内速度的横向变化率很大，黏性力的影响较大。随着边界层沿程发展，层内流态也沿程变化，历经层流、过渡区最后达到紊流状态，如图4所示。而且在过渡区和紊流边界层与平板之间还有更薄的一层，称为黏性底层。

图4 风电叶片及其轮毂位置关系

平板边界层由层流部分、过渡部分和湍流部分组成，但过渡区往往只占极小的部分，可看成一个点。所以只分析层流和湍流部分。本文参考一组1.2 MW风电叶片数据，其叶根处叶素旋转半径为r，弦长约为5.5 m，空气密度为1.225 kg/m3，空气的运动黏度为1.5×105Pa/s，额定风速12 m/s，估算出叶根处翼型表面气流雷诺数为：

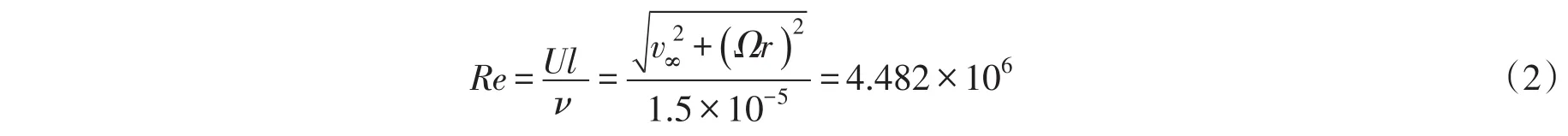
根据文献［16］，平板上层流变为层流时的临界雷诺数是：

根据式（3），得到叶根处翼型表面上转捩点的位置为：

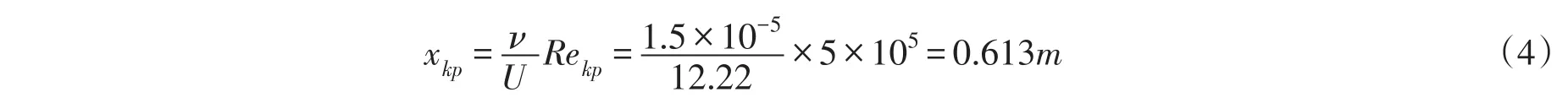
式中：xkp为边界层前缘（x=0）到转捩点的距离，Rekp为转捩雷诺数。

因此，额定风速下翼型上同时存在层流和湍流，但是层流所占比例极小，因此本文全部按照湍流计算摩擦阻力。边界层以外，黏性完全可以忽略，即使应用无黏流理论来分析流动，也可以达到很高的精度。

对于平板的定常流动，虽然空气的黏性很小，但边界层内空气的速度梯度变化很大，导致由于流体黏附在平板表面上，速度从零沿薄层横向迅速增至外流速度U［17］。

取边界层上一块宽度为1的微元控制体，其如图5所示，OABC为面积区域，OA表示流体入口，高度为h，曲线AB表示边界层的分隔线，δ()x表示边界层x处的厚度。

图5 边界层微元控制体

FD为流体剪应力τ在x方向上对平板壁面的合力，τ沿着x方向积分，有：

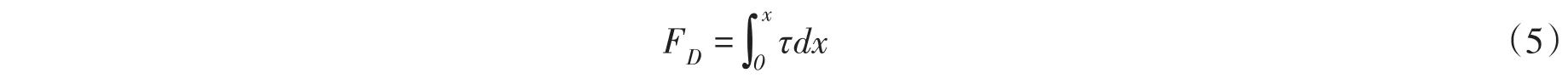
由定常流动的动量方程，得到：

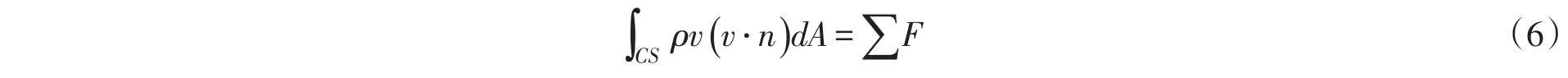
在x方向上的分量为：

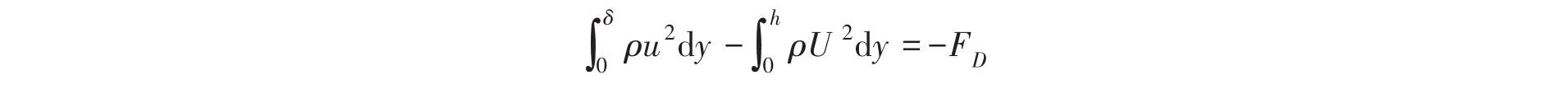
所以有：

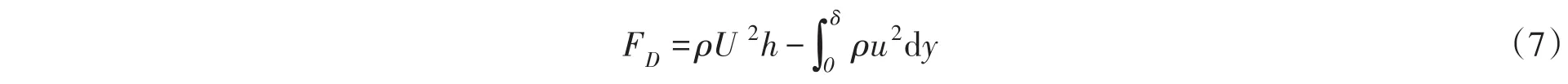
根据质量守恒，通过OA和BC两个面的流体质量相等，得到：

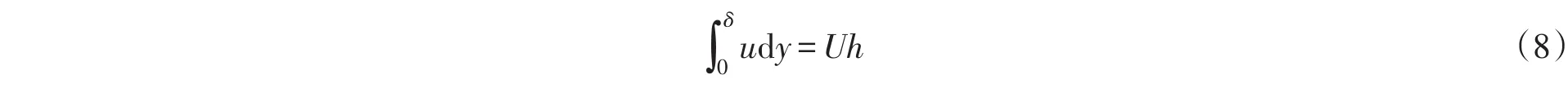
将式（8）代入式（7）中，得：

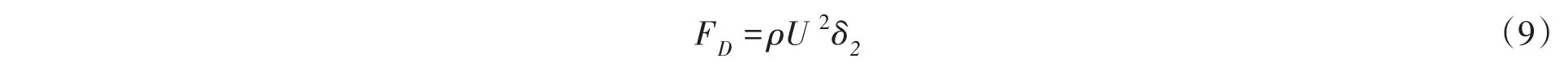
对式（9）求导：

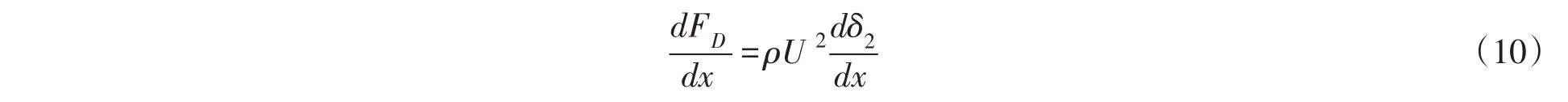
由式（5）得到：

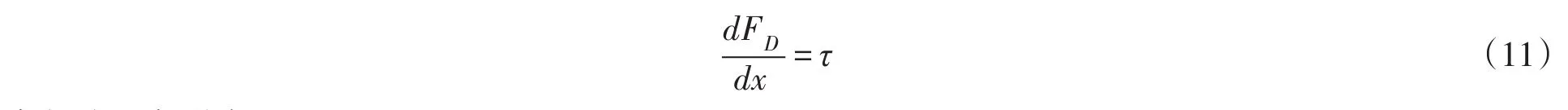
式（11）可变形为：

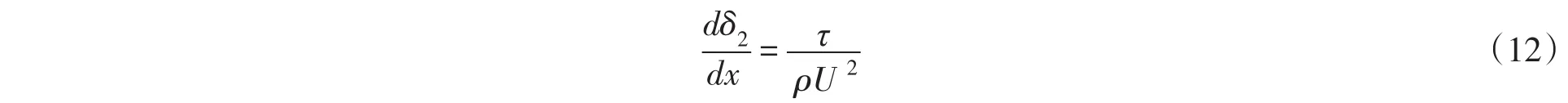
式中δ2为边界层的动量厚度。由式（12）可知，只要知道边界层的动量厚度，即可求出平板上边界层上的切应力。根据动量厚度公式可知，动量厚度取决于流速分布，所以要先确定边界层内部的速度分布。参考黏性流体动力学文献［15］，再结合叶片表面气流的湍流状态，边界层选用1/7为指数的流速分布：

式中δ为边界层内流体速度。求得边界层动量厚度为：

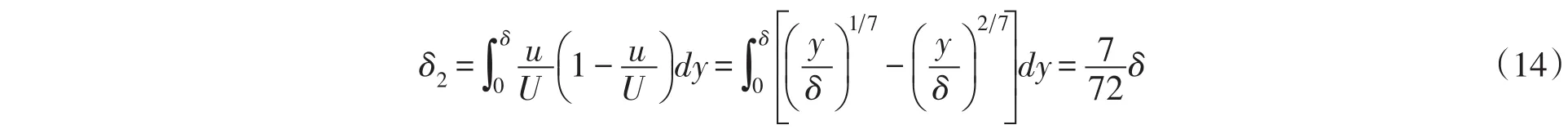
将式（14）代入式（12），得：

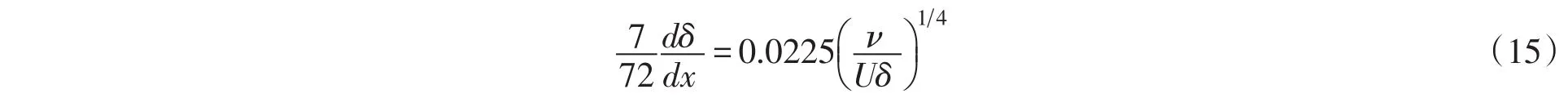
从平板前缘开始，对式（15）积分，并结合边界条件x=0，δ=0，求得：

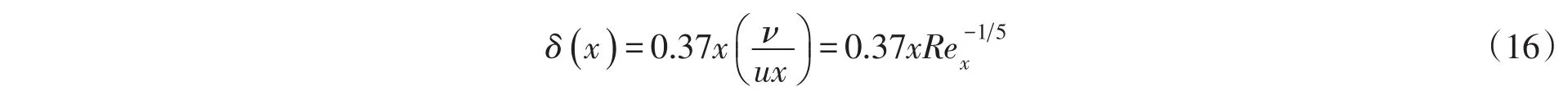
δ()x为平板上距离O点x处的边界层厚度，Rex为微元平板上流体的雷诺数。由滑壁面圆管的湍流切应力：

圆管的直径无穷大时，圆管将变成一个平板，此时切应力为：

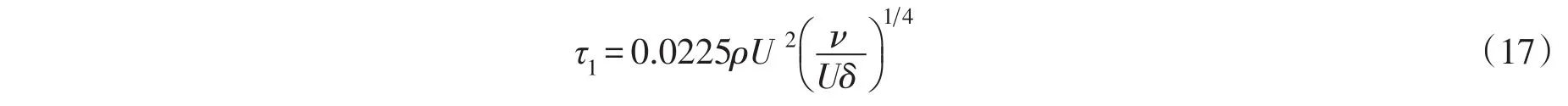
联立式（5）、式（16）、式（17），得到长度为l，宽度为dr的平板上的总阻力：

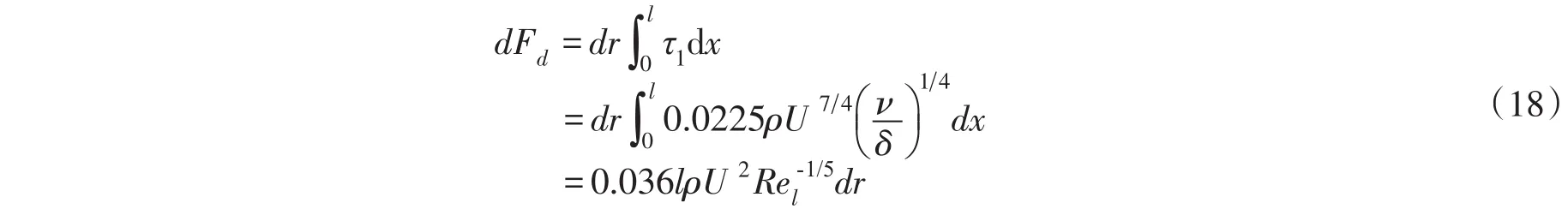
式（18）就是宽度为dr，长为l的平板上摩擦力的计算公式，Rel为平板雷诺数。

2.3 叶片气动摩擦力计算 （1）叶片迎风面摩擦力。考虑到叶片翼型的桨距角β和攻角α，因此来流对风轮产生的实际摩擦阻力矩为：

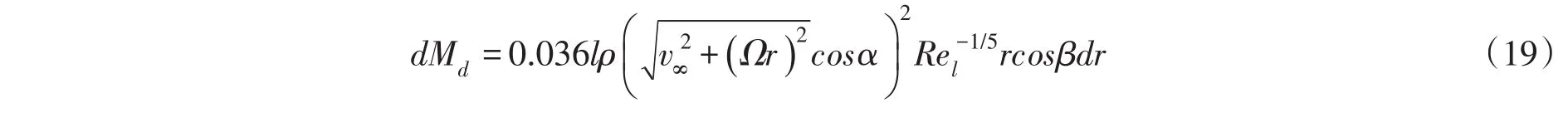
根据文献［1］，可将距离叶片旋转轴线r处dr叶片微段的叶素弦长设为：

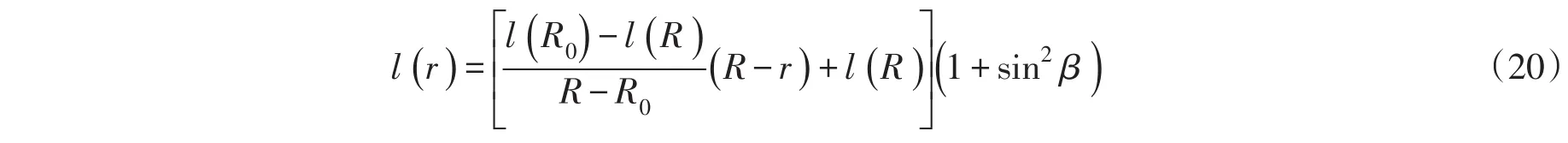
式中：l(r)为叶片径向r处的弦长，l(R0)为叶根处弦长，l(R) 为叶尖处弦长。将式（20）代入式（19），并沿叶片半径积分得：

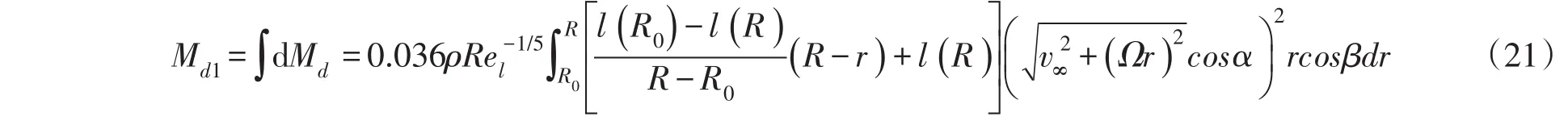
式（21）即为整个叶片迎风面上的摩擦力矩公式。由于额定风速下攻角和桨距角很小约去，计算得到单个叶片迎风面的摩擦力矩：

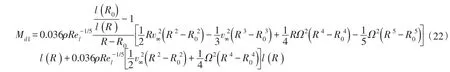
（2）叶片背风面摩擦力。对于背风面，假定背风面空气是静止的，但是由于风轮的旋转使得空气获得一个沿着弦长向后缘的相对速度Ωrcosβ，将得到的力投影到旋转平面上，就能得到摩擦力对旋转轴的摩擦力矩。迎风面背风面弦长相同，根据式（18）、式（20）得到背风面上的摩擦力：

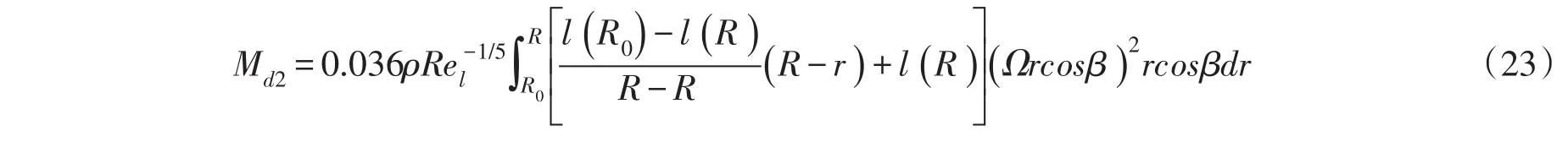
式（23）求积分，得：

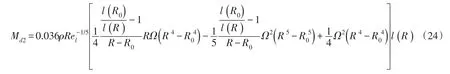
3 考虑摩擦力的弦长计算

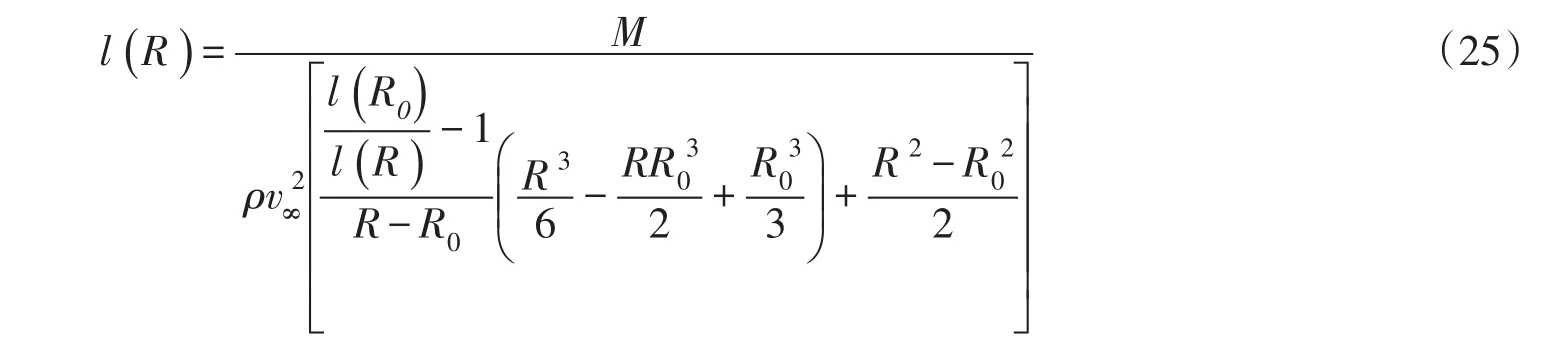
令式（25）的分母为m，即：

联立式（22）、式（24）和式（25），考虑摩擦力作用下叶尖的弦长为：

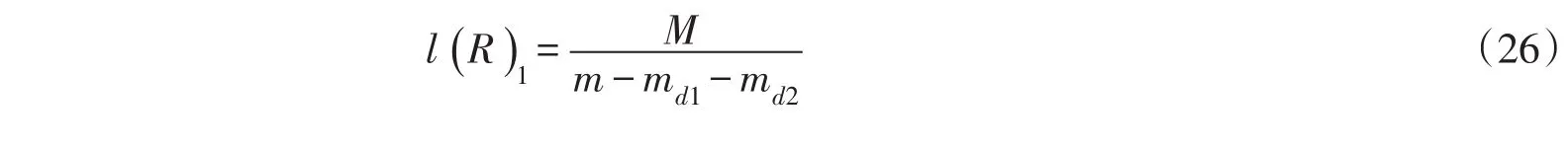
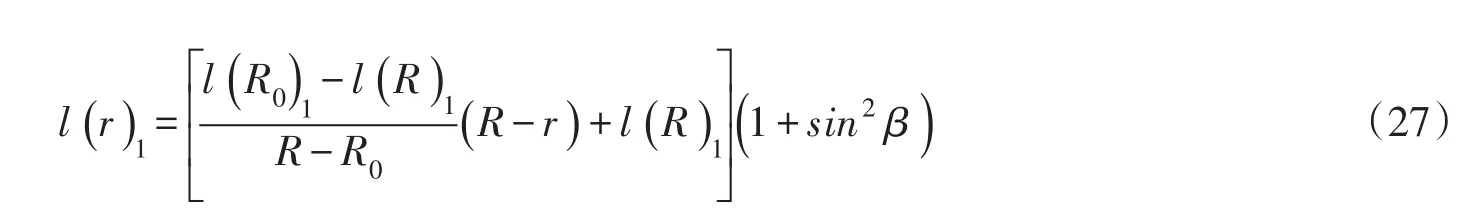
距旋转轴线r半径处dr叶片微段的叶素桨距角β为：

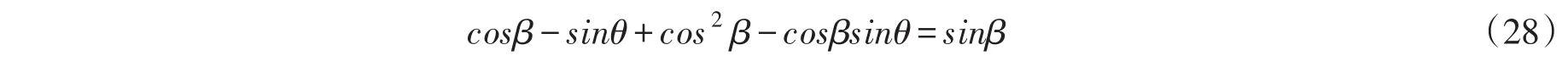
式（26）、式（27）、式（28）就是经过空气摩擦修正的叶片弦长、桨距角计算模型，由式（22）可知，空气流过叶片表面会给风轮产生一个摩擦力矩，要在额定风速时达到风电机组额定发电功率，需要增加一部分弦长来补偿摩擦消耗，因此与原叶片弦长设计理论相比，考虑摩擦得到的弦长更长，其对比如图6所示。

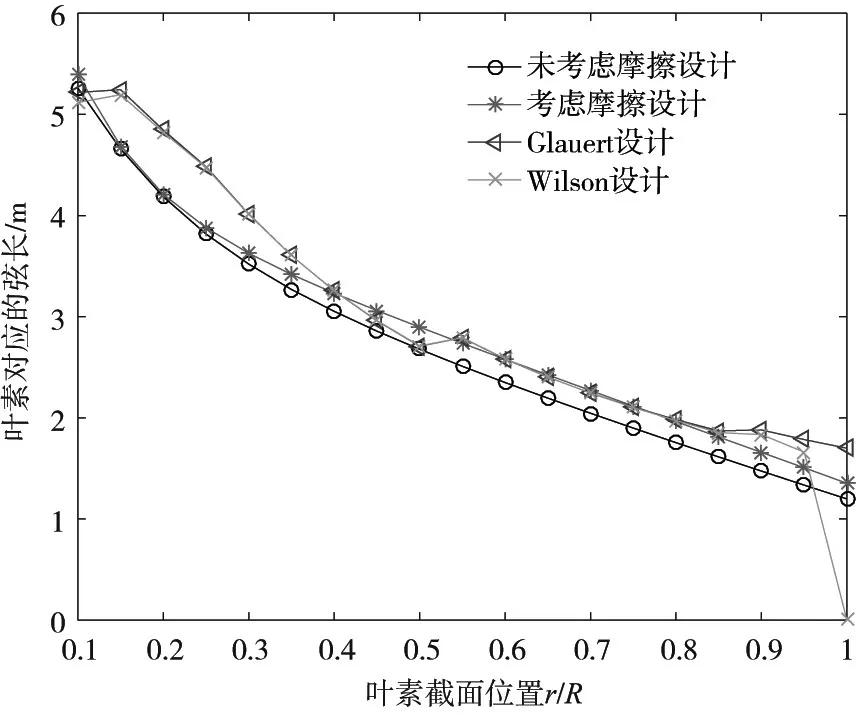
图6 四种理论模型得到的叶素弦长比较

由图6可知，考虑摩擦的弦长比文献［1］中的弦长增加，在r/R为0.4～0.55区间内弦长大于Glauert设计理论和Wilson设计理论，在额定功率相同的的情况下，弦长在总体上比Glauert缩短约6%，比Wilson缩短约3%，高于未考虑摩擦设计约7.81%，设计出的叶片质量更轻，Glauert和Wilson设计理论得到的弦长在0.5R和0.85R处有弯折，这是由于Glauert和Wilson设计理论考虑翼型形状对叶片气动性能的影响，在设计叶片时各段选取不同的翼型，每个翼型的最佳攻角和气动性能都不一样，这造成了弦长分布曲线发生弯折，摩擦修正的弦长设计理论有效提高了叶片的顺滑度，降低叶片加工制造难度。

4 风能功率与风能利用率计算结果与分析

为验证理论的正确性，对未考虑摩擦得桨距角弦长设计理论、摩擦力修正设计理论、Glauert设计理论和Wilson设计理论采用Solidworks建立三维模型，模型的设计参数如表1所示。

表1 1.2MW风电机组设计参数

根据表1的风电机组设计参数，计算得到未考虑摩擦弦长设计、摩擦修正设计、Glauert设计、Wilson设计共4种方法下的弦长和桨距角，并对4种方法得到的叶片建模，导入Fluent，在额定转速22.2 rpm，风速6～14 m/s共5个风况条件下，选用SST湍流模型［18］进行模拟，对得到的数据进行计算整合，得到了不同风速下风轮功率和风能利用率分别如图7和图8所示。

图7 风轮输出功率曲线

由图7和图8可知，在风速低于9 m/s时，摩擦修正设计得到的风轮功率和风能利用率都高于不考虑摩擦的桨距角弦长设计理论、Glauert设计理论和Wilson设计理论，说明在低风速下摩擦力修正设计的叶片具有更好的气动性能，所以表明摩擦力修正设计的风电机组具有更低的启动风速。

图8 风能利用率曲线

风速在9～11 m/s范围内，摩擦修正得到的风轮风能利用率略低于Glauert设计，高于未考虑摩擦的桨距角弦长设计，除Wilson设计外，其他三种风轮气动性能区别不大。

根据数值模拟结果，在风速高于11 m/s时四个机组都超过了额定功率，根据图8，在高于10.5 m/s的风速区间风能利用率开始逐渐降低，且低于Glauert设计，因此考虑摩擦设计不适用于高风速风电机组，只适合在低风速地区的中小型风电机组叶片设计上采用。

5 结论

本文研究来流对风电机组叶片旋转产生的摩擦阻力，分别建立迎风面、背风面摩擦力计算模型，并用摩擦力修正弦长，得到低风速下更良好的气动性能。

（1）应用黏性流体边界层理论对空气流过叶素迎风面和背风面产生的摩擦力进行了分析计算，叶片表面同时存在层流和湍流两种流态，但层流所占比重极小，按全湍流计算，基于叶片桨距角和弦长设计理论得出叶片摩擦力计算公式。

（2）摩擦力与来流速度的平方成大致成正比，且迎风面摩擦力占总摩擦力的比重约为90.5%。

（3）考虑摩擦设计的叶片弦长高于原设计约7.81%，但仍分别比Glauert设计和Wilson设计低6%和3%，同样的输出转矩下叶片可以做得体积更小，重量更轻。在小于9 m/s的低风速工况下，风轮功率、风能利用率均高于Glauert设计和Wilson设计，因此摩擦修正的桨距角弦长设计理论具有较好的低风速性能，在风速高于11 m/s时，风轮超出额定输出功率，此时风能利用率减小并低于Glauert设计，因此本文模型不适合在高风速地区采用。

（4）模型的不足之处在于把复杂的三维流动假定为二维流动，把大部分湍流假设为全部湍流，翼型的曲线看成一条直线，这必然导致与实际摩擦力的偏差，从数值模拟的结果来看更符合叶片的实际工况，要确定上述假设对摩擦力计算的影响仍需进一步的研究与实验。