颗粒形状对烧结矿填充床内渗透系数和阻力系数的影响

(北京科技大学能源与环境工程学院，北京，100083)

高能耗和高排放是钢铁工业的两大特点[1-3]。在中国，烧结工序的能耗占整个钢铁行业的10%～15%，仅次于炼铁工序[4]，而烧结矿显热占烧结工序余热总资源的70.87%[5]，因此，烧结矿显热的高效回收对降低烧结工序乃至整个钢铁行业的能耗都具有重要的意义。目前，主要通过环冷工艺回收烧结矿余热，但是，环冷工艺的漏风率高，且余热回收率仅29.79%[6]。基于此，近年来，SUN等[7]借鉴干熄焦工艺提出了烧结矿竖罐式冷却工艺。竖罐式冷却工艺的漏风率接近于0，且可将余热回收率从30%提高到80%左右[6]。然而，竖罐式冷却技术应用成功的案例很少。而竖罐式冷却工艺的可行性取决于气固传热和气体流动特性这2个方面[7-8]。气体流动不仅是气固传热的基础，还直接决定着匹配风机的能耗，因此，研究烧结矿填充床内气体阻力特性对于从经济角度分析工艺的可行性十分重要。

迄今，ERGUN关于填料床内流动阻力的研究最具代表性，并提出了ERGUN方程[9]。但ERGUN方程只能准确地预测球形颗粒填充床内的流动阻力[10-11]。在预测圆柱等规则颗粒时，相对误差为10%～30%[12-14]。而在预测岩石等不规则颗粒时实测值比预测值高1.5～5.0 倍[13]。这主要归因于颗粒形状的差异[10]。由于球体各向相同，而不规则颗粒各向相异，这导致不规则颗粒的床层结构比球形颗粒更复杂[10]。大多数学者认为不存在普适性的阻力关联式，对于不同的颗粒均需单独测量获得。

由于烧结矿颗粒的形状极不规则[15]，近年来，一些学者研究烧结矿填充床内气体流动特性[8,15-26]。研究表明烧结矿填充床内气体流动阻力与高度呈线性关系[17]，而与气体流速呈二次关系[16-19]。其次，还发现当床径比(床层直径与粒径比)大于19时，可以忽略壁面效应，而当床径比小于19 时，壁面效应会导致气体阻力降低[20]。此外，粒度分布对填充床内气体流动阻力也有一定影响[23-25]，双粒度烧结矿填充床比单粒度填充床更易于进入湍流区[23]。前人的工作主要研究了料层高度、气体速度和壁面效应等因素对气体阻力的影响，而关于颗粒形状对填充床内气体流动状态和阻力的研究很少，不够系统，也不便于实际应用。为此，本文作者首先表征烧结矿的颗粒特性，其次利用自制试验台测量烧结矿填充床内的气体流动阻力，并分析颗粒形状对床层内阻力特性、渗透性和气体流动状态的影响，最后获得利用形状因子修正的阻力关联式，以期为烧结矿竖罐式冷却工艺的可行性分析提供理论基础。

1 实验与方法

1.1 实验装置与步骤

测量烧结矿填充床内气体流动阻力的实验装置如图1所示。由图1可见：实验装置由圆柱形填充床、送风系统和测量采集系统组成。圆柱形填充床的内径和高度分别为400 mm和1 000 mm。首先，本文选用高压变频风机(型号为HRD 65FU-100/7.5)进行送风。通过调节风机频率，从而精确地控制风机流量。其次，选用涡街流量计(型号为LUGB1315C-P3Z)和压力变送器(型号为CGYL-202)分别测量风机流量和气体压力，并通过无纸记录仪(型号为LD-300G)采集数据。为了消除温度和压力的干扰，采用温压补偿式流量计，测量范围和精度分别为300～3 000 m3/h和1.0%。压力变送器长度、测量范围和精度分别为650 mm，0～5 kPa和0.5%。

在测试中，气体的运行状态与烧结矿竖罐式冷却工艺相同，均是先从床层底部将气体鼓入，然后从顶部出口排出。其次，在床层底部安装了开孔均匀的布风板，如图1所示。此外，沿着床层轴向设置6 个相互间隔200 mm 的测压孔。为了降低壁面效应，在每个测压孔位置上沿着径向均匀地设计9个测点。

图1 烧结矿填充床内气体流动阻力测量装置的示意图Fig.1 Sketch map of experimental apparatus for measuring gas flow resistance in sinter packed bed

1.2 实验材料

本研究使用的烧结矿来自邯郸钢铁公司。首先利用标准筛[27]通过筛分获得烧结矿的粒度分布，如图2所示。观察到5批烧结矿的粒度分布基本一致，尤其是分布在(5，60]mm 的烧结矿质量占总质量的85.24%，所以，本文将粒径在(5，60]mm的烧结矿作为研究对象，并每间隔5 mm设一种粒级，共11 种。图3所示为烧结矿筛分前后的实物图。对每种粒度的烧结矿还设计了气体流量范围较广的测试工况，如表1所示。

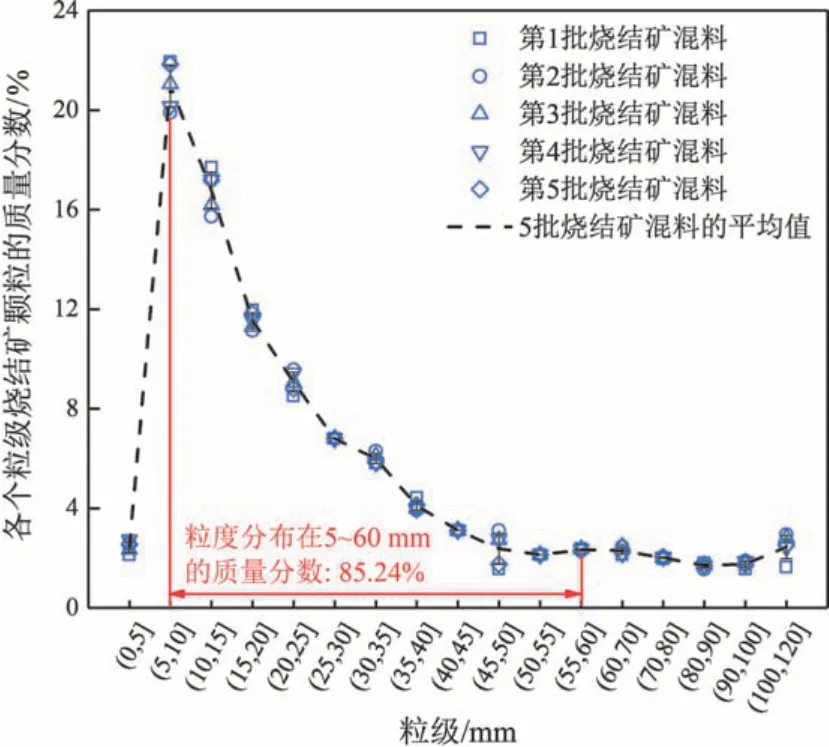
图2 邯郸钢铁公司烧结矿样品的粒度分布Fig.2 Particle size distribution of sinter samples from Hansteel Company

1.3 颗粒特性的表征方法

为了详尽地描述烧结矿，本文对烧结矿的颗粒特性进行了表征。首先利用排水法[28]测量每个粒级烧结矿的表观密度，如式(1)所示。

式中：ρa为烧结矿表观密度，kg/m3；ρw为试验温度下蒸馏水密度，kg/m3；m1和m3分别为干烧结矿和湿烧结矿的质量，kg；m2为烧结矿和试验篮在水中的质量，kg；m4为试验篮在水中的质量，kg。

图3 筛分前后烧结矿颗粒的实物图Fig.3 Practicality pictures of sinter particles before and after screening

表1 11种粒级烧结矿填充床的测试工况Table 1 Test conditions of 11 kinds of sinter packed beds

其次，通过称重法[29]测量烧结矿的堆积密度：

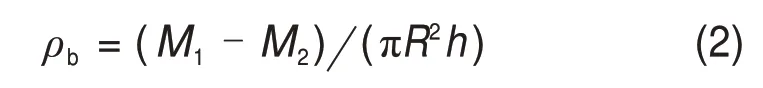
式中：ρb为烧结矿的堆积密度，kg/m3；M1为烧结矿和试验容器的总质量，kg；M2为试验容器的质量，kg；R为试验容器半径，m；h为试验容器中烧结矿料层的高度，m。

此外，每个粒级的烧结矿均随机挑选50 颗，利用等体积法[20,22]可获得烧结矿的当量粒径：

式中：dp为烧结矿的当量粒径，m；ms为单颗烧结矿的平均质量，kg。

本文还分别采用式(4)[22-23]和(5)[14]获得床层空隙率ε和烧结矿的形状因子φ：

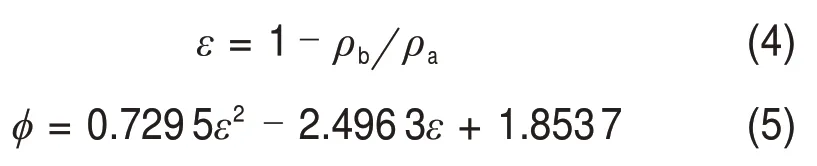
φ反映了颗粒偏离球形的程度。对于球形颗粒来说，φ=1。φ越接近于1，表明颗粒偏离球形的程度越小。

2 数据分析

2.1 数据处理

最初，气体通过填充床的流动阻力一般利用Forchheimer方程进行计算[23]：

式中：K为渗透系数，与黏性阻力相关，m2；F为Forchheimer 系数，也称作惯性拖曳系数，与惯性阻力相关；ΔP为气体通过料层的阻力，Pa；L为料层高度，m；ΔP/L为单位料层高度的气体阻力，Pa/m；ug为气体的表观速度，m/s；ρg为密度，kg/m3；μ为动力黏度，Pa·s。此外，为了描述床层内气体的流动状态，常用惯性阻力与总阻力的比值X来判定[23]：

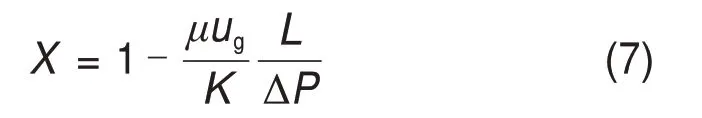
SEGUIN等[30]认为当X>0.70时，气体的流动状态由层流转变到过渡态；当X>0.91 时，则由过渡态进入到湍流。由于Forchheimer 方程的经验系数K和F与颗粒特性无关，且在实际应用中局限性较大。因此，含有颗粒特性参数的ERGUN方程为[9]

式中：k1和k2分别为黏性阻力系数和惯性阻力系数。由于烧结矿形状极不规则，本文在阻力方程中考虑形状因子[17]：

为了简化上式，引入阻力因子fp和颗粒雷诺数Rep[21]：

可将式(9)整理为量纲一形式：

由式(12)可知，阻力因子fp与颗粒雷诺数Rep呈线性关系。

2.2 误差分析

本文利用误差传递理论[22]估计参数的不确定度。假设参数y与k个变量的关系为

式中：x1，x1，x3，…，xk为k个独立变量。y的绝对不确定度Δy与每个变量的绝对不确定度(Δx1，Δx1，Δx3，…，Δxk)的关系为

参数y的相对不确定度的表达式为

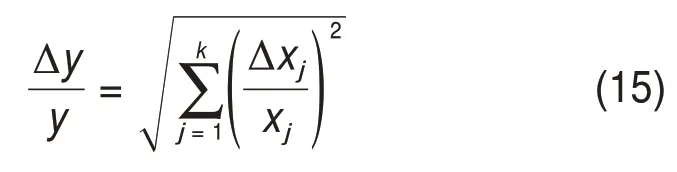
表2所示为通过上述方法获得的本研究参数的相对不确定度。

3 烧结矿颗粒特性的表征结果

图4所示为利用上述方法获得的烧结矿颗粒特性参数。由图4可见：

1)颗粒的表观密度随着粒度增加而呈指数衰减。由于烧结矿内部闭孔数量会随粒度增加而逐渐增多，导致表观密度会随之降低，但当粒级大于40 mm 时，颗粒内闭孔数量基本恒定，导致表观密度基本不变。

2)堆积密度也随着粒度增加呈指数衰减。这由2个方面引起，即表观密度也呈现类似变化以及颗粒的不规则程度随着粒度增加而增加，导致颗粒在堆积过程中易出现架桥现象。同时，这也是造成空隙率随着粒度增大而增大的原因。

3)当量粒径随着粒度增加而增加。但由于颗粒比表面积会随着不规则程度增加而增大，造成当量粒径偏离平均粒径。

4 床层内流动阻力的影响因素

4.1 料层高度

图5所示为料层高度(L)对4种烧结矿单位料层高度阻力(ΔP/L)的影响。由图5可见：3 种料层高度(L=200，400 和600 mm)下单位料层高度阻力基本一致。因此，可以忽略料层高度对单位高度阻力的影响。由于同一粒级下颗粒的粒度和形状基本相同，导致床层空隙率沿着轴向分布比较均匀。这使得相同料层高度会对气体流动产生相同的阻滞作用。

4.2 气体表观速度

图6所示为不同粒级烧结矿填充床内单位料层高度阻力(ΔP/L)与表观气体速度(ug)的关系。由图6可知：不同粒度下ΔP/L均随着ug增加而增加。通过ΔPL=a·ug+b·ug2 形式进行拟合，发现相关系数R2均大于0.997 0，表明ΔP/L与ug之间具有良好的二次关系。由于ug增加加剧了气体与颗粒的碰撞，破坏流动的边界层，因此，与速度呈一次关系的黏性阻力被削弱，而与速度呈二次关系的惯性阻力逐渐占据主导地位。

表2 本研究参数的相对不确定度Table 2 Relative uncertainty of parameters in this work

图4 不同粒级烧结矿的颗粒特性Fig.4 Particle characteristics of sinter with different particle sizes

图5 料层高度(L)对4种不同粒级烧结矿单位料层高度阻力(ΔP/L)的影响Fig.5 Effect of bed height(L)on resistance per unit bed height(ΔP/L)of four kinds of different particle sizes

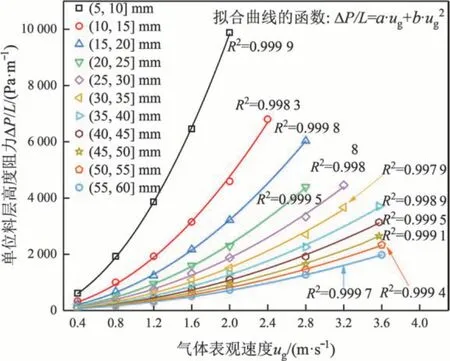
图6 不同粒级烧结矿填充床内单位料层高度阻力(ΔP/L)与表观气体速度(ug)的关系Fig.6 Relationship between resistance per unit bed height(ΔP/L)and superficial gas velocity(ug)under sinter packed bed with different particle sizes

4.3 当量粒径、空隙率和颗粒形状

图7 不同表观气体速度下单位料层高度阻力与颗粒特性参数的关系Fig.7 Relationship between resistance per unit bed height and particle characteristic parameters at different superficial gas velocities

图7所示为不同气体表观速度下单位高度阻力(ΔP/L)随着当量粒径(dp)、床层空隙率(ε)和形状因子(φ)的变化。首先，通过指数函数拟合，发现相关系数R2均大于0.990 0，表明ΔP/L与3 个因素均呈良好的指数关系，且三者之间存在着一定的关联，其次，观察到ΔP/L随着当量粒径和空隙率增大而衰减，而随着形状因子增大而增大。由于颗粒的不规则程度随着粒度增大而增加，导致空隙率增大，这使得相同表观速度下大颗粒床层内的气体真实速度反而更小，湍流现象更少，同时，这也引起气体的流动更加有序，导致流动通道的长度更短。因此，单位料层高度阻力随着空隙率增加而降低。此外，由图4(a)可知空隙率的增幅随着粒径增加而降低，造成单位高度阻力的降幅也越来越小。

5 颗粒形状对床层宏观特性的影响

基于图6所示实验结果，获得不同粒级烧结矿还原阻力(ΔP/(L·ug))与气体表观速度(ug)的关系，如图8所示。首先，利用最小二乘法进行拟合(R2均大于0.99)，发现不同粒级下还原阻力均与气体速度呈良好的线性关系；其次，结合Forchheimer 方程，获得了不同粒级烧结矿的渗透系数K和惯性拖曳系数F，如表3所示。由表3可知：渗透系数随着形状因子减小即粒度增加而增加。渗透系数表征一定压差下气体通过床层的流量。

由图8可知：相同还原阻力对应的气体速度随着粒度增加而增加。由于颗粒的不规则程度随着粒度增加而增大，导致颗粒在堆积过程中更易形成较大通孔，气体越易于穿透床层。惯性拖曳系数则与渗透系数相反，表明较大颗粒下惯性效应反而更弱。由于大颗粒床层内空隙率较大，导致同一表观速度下气体的真实速度反而较小，削弱了惯性作用。

图8 不同粒级烧结矿填充床内下还原阻力(ΔP/(L·ug))与表观气体速度(ug)的关系Fig.8 Relationshipbetweenreducedresistance(ΔP/(L·ug))and superficial gas velocity(ug)in sinter packed with different particle sizes

通过式(7)，获得了不同粒度下惯性项比例X与气体表观速度的关系，如图9所示。由图9可见：1)随着气体表观速度增加，不同粒度下X从分散分布到逐渐聚集。由于不同粒级烧结矿的形状不同，导致床层结构不同。这表明颗粒形状会显著地影响气体的流动状态，尤其是在较低的气体速度下。2)床层内气体流动大部分处于过渡区和湍流区。这归因于烧结矿形状不规则，极易破坏流动的稳定性。此外，粒径为(5，10]mm 和(55，60]mm烧结矿填充床内气体转变到湍流区的速度分别约为1.8 m/s 和3.6 m/s，表明小粒级烧结矿床层内的气体流动会更早地转变到湍流。由于小粒级烧结矿床层空隙率较小，造成同一表观速度下小粒级烧结矿床层内气体的真实速度反而更大。

表3 11种粒级烧结矿填充床的宏观特性Table 3 Macroscopic characteristics of 11 kinds of sinter packed beds

图9 不同粒度下惯性项比例(X)随着表观气体速度的变化Fig.9 Change of proportion of inertial resistance(X)with superficial gas velocity at different particle sizes

6 床层内气体流动阻力关联式分析

首先将不同粒级烧结矿的实验数据代入式(12)，利用最小二乘法获得了各粒级下黏性阻力系数k1和惯性阻力系数k2随着形状因子的变化，如表4所示。由表4可知相关系数R2均大于0.995，表明阻力因子fp与颗粒雷诺数Rep具有良好的线性关系。其次，将阻力系数k1和k2拟合成形状因子φ的函数(图10)，具体表达如下：

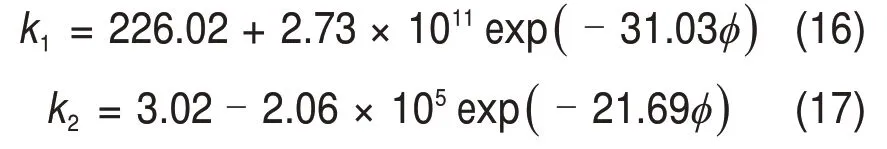
图10 黏性阻力系数(k1)和惯性阻力系数((k2)与形状因子(φ)的关系Fig.10 Relationship between viscous resistance coefficient(k1)and inertial resistance coefficient(k2)versus shape factor(φ)

最后，将k1和k2代入式(9)，可得预测烧结矿床层内气体阻力的通用关联式：

图11所示为单位高度阻力的实测值与利用式(18)和ERGUN方程获得预测值的对比。由图11可见：1)ERGUN 方程的预测值平均低于实测值69.03%，表明ERGUN 方程不适合预测不规则颗粒。2)本文预测值与实测值之间的相对误差基本都在8.00%以内，平均相对误差为3.65%，因此，形状因子修正的阻力关联式可以较好地预测烧结矿填充床内的气体流动阻力。

表4 不同形状因子下黏性阻力系数(k1)和惯性阻力系数(k2)Table 4 Viscous resistance coefficient(k1)and inertial resistance coefficient(k2)under different shape factors

图11 单位高度阻力(ΔP/L)的实测值与预测值(本文和ERGUN)的对比Fig.11 Comparison between measured value and predicted value(present work and ERGUN)of resistance per unit bed height(ΔP/L)

7 结论

1)随着烧结矿粒度增加，颗粒的表观密度和堆积密度呈指数衰减，而空隙率和不规则程度则逐渐增加。

2)单位料层高度阻力随着形状因子减小即颗粒的不规则程度增加而呈指数关系衰减。这是因为颗粒的不规则程度增加导致床层内的空隙更大，气体的湍流程度更小。

3)烧结矿的不规则程度越大，床层的渗透系数越大，导致气体更易于穿透床层。同时，不同粒级烧结矿床层内惯性项比例X在较低速度下呈分散分布，但随着气体速度增加而增大且逐渐趋于一致。

4)利用本文形状因子修正的阻力关联式可以较好地预测烧结矿填充床内的流动阻力，预测值和实测值之间的相对误差均小于8.00%，平均相对误差为3.65%。