大区域无人机影像全自动拼接的三维重建

韦程文

（深圳市建设综合勘察设计院有限公司，广东 深圳 518000）

0.引言

在空间信息科学技术不断发展的过程中，遥感影像数据在各社会领域中被广泛使用。无人机（UAVs）遥感的主要优势为投入低、操作方便、灵活、适用范围广等，解决了航空遥感在指定应用范围中快速得到高分辨率影像需求中的空间问题。目前，我国低空域逐渐对民用开放，无人机遥感技术也在不断地发展，其使用具有较大的潜力，如何实现无人机数据量图像快速鲁棒全自动三维处理尤为重要[1]。早特征点检测、鲁棒性估计算法、运动恢复结构重建算法等不断发展的过程中，基于图像的三维重建技术也在不断发展，从而使基于图像的自动三维重建技术被广泛使用[2]。以此，本文针对无人机图像数据特点，提出基于三维重建的大区域无人机影像全自动拼接方法，实现大数据无人机图像快速三维重建。

1.无人机图像数据的特点

无人机搭载相机大部分都是固定镜头非量测型普通数码相机，在得到图像的时候还会对图像对应经纬度坐标进行记录，并且记录飞行速度、方向角和高度等信息。无人机为了对飞行稳定性进行保证，要实现稳定平台信息的设计，并且提供俯仰角、横滚角信息。因为无人机载和和成本的限制，装载导航GPS 精度为10m 左右，辅助数据记录角信息精度比较低。无人机在飞行前要设计航线规划轨迹，实际航飞轨迹不规则，部分飞行任务偏离原本的航线，并且在飞行过程中姿态并不稳定，倾斜比较大。对于拍摄地形来说，能够利用Google Earth 数据或者公开DSM 数据得到此区域相应精度在30m 左右的地形高程数据。为了避免飞行过程中漏拍，无人机影像的重叠率比较高，在重建图像过程中得到航向重叠在70%以上，旁向重叠在30%以上，以此飞行任务得到大量的影像，部分大场景都会拍摄得到千张影像[3]。

无人机图像数据特点为：（1）在使用过程中得到无人机定焦镜头，固定焦距值，并且利用严格标定消除畸变，得到相机内参数信息；（2）有10m 左右精度位置辅助信息；（3）存在粗略地形高程数据；（4）存在低精度姿态辅助信息，一般在10°以内；（5）具有丰富地面图像数据纹理，适合自动匹配重建；（6）保证高重叠率[4]。

2.高光谱影像拼接的三维重建

2.1 影像拼接流程

无人机高光谱影像拼接流程，整体拼接流程根据处理影像波段数包括三部分（如图1 所示）。因为不同波段成像传感器位置不同和成像时间的不同，高光谱影像不同波段具有配准误差，所以在拼接前实现影像配准处理，配准之后同幅影像各个波段数据利用统一姿态参数进行描述。因为后续步骤目的就是对影像姿态参数进行计算，得到拍摄区域中空间信息密集点云，利用单波段数据处理得到几何信息。通过数字微分实现影响波段数据几何纠正，镶嵌得出拍摄区域拼接影像[5]。

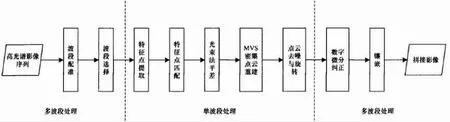
图1 无人机高光谱影像拼接流程

为了实现全自动波段配准，本文方案将中间波段数据作为基准数据，通过二次多项式将其他波段和基准波段几何关系充分描述，实现各波段数据和基准数据的特征点匹配，以匹配特征点坐标实现二次多项式系数拟合，以此实现各波段数据几何配准。高光谱数据波段配准前后的对比，（如图2 所示）。通过图2 可以看出来，配准之前具有配准误差，影像重影，通过二次多项式配准之后的各个波段影像具有良好的重叠，没有重影问题，同个高光谱数据各个波段利用统一姿态参数对空间位置姿态进行描述。选择波段能够在高光谱数据中选择一个波段数据，生成后续点云，一般在丰富纹理波段中能够提取大量的特征点数量，但是本文并没有使波段数据量作为选择波段评价标准，主要是因为对大区域影像序列分析，某个影像中某波段信息量丰富，并不代表此区域全部影像中此波段信息量都比较丰富。所以，本文选择高光谱影像中间段选择后续特征点[5]。

图2 高光谱数据波段配准前后的对比

2.2 提取特征点

本文利用改进SIFT方法将特征点进行提取，SIFT特征点的主要特点为光照、旋转、尺度等不发生改变，具有良好鲁棒性，能够满足宽基线匹配，所以满足MAV采集图像姿态不稳定问题。特征点匹配过程中利用KD树使搜索效率得到提高，并且使用从粗到精的匹配策略，对高冗余度数码照片集进行处理[6]。

2.3 分析运动获取结构

SFM属于计算机视觉领域标准技术，针对照片之间特征点的匹配关系，利用非线性优化方法对相机参数和稀疏三维点云进行计算。通过贪婪搜索SFM方法和递进方法逐台的添加相机，初始相机对标标定使用五点法对稳定初值进行确定，避免非线性在局部极值中收敛，得出错误相机标定结果[7]。

2.4 多视立体三维重建

MVS为近几年发展的计算机视觉技术，通过已标定多视角照片实现三维重建，一般方法为深度图、基于法向量、面片融合的方法。本文使用深度图融合三维重建方法，重点为对立体图像深度图的恢复进行确定，并且使高可靠性的多深度图进行融合，从而得出密集三维点云，以下为具体过程：

给定某图像对为Yi=(Is，It)，基线比较大，利用DAISY描述子和极限量测相识度，对稠密深度图。DAISY为通过一系列梯度直方图串联构成，计算划分成为多个独立方向梯度计算，之后使每个方向梯度模值综合构成方向直方图，此计算过程利用各方向梯度实现不同尺度高斯滤波。DAISY得出与SIFT直方图计算过程相类似的不变性，但是效率比较高，满足图像逐个像素点对描述子进行计算，所以满足密集匹配生成深度图。

为了使计算效率得到提高，直接利用DAISY匹配度分支对一幅图像像素x具有深度d概率进行计算：

式中，指的是图像像素x对应描述子；在另一幅图像中的描述子，假设深度为d。分布函数陡峭度通过进行控制；Z指的是归一化常数，保证概率和为1。为了决定是否使深度值为某像素赋予，根据对极线均匀采样得到最大概率前两位，对两者比值进行计算：

在RΧ 比某阈值要大的时候，此深度值也是有效的，本文实验中所使用的阈值为0.75，结果表示所产生外点比较少。生成稠密点云，通过泊松重构方法生成3D表面格网模型[8]。

2.5 建筑物纹理重建

收集数据，得出描述图像轮廊的便捷模型。但是要创建真实三维模型，并且实现建筑物表面纹理重建。本文对简单建筑物模型进行考虑，通过多边形顶面和矩形侧面构成。所以，纹理重建要和其对应，也就是顶面纹理与侧面纹理的重建。通过序列影像重建建筑物模型在两幅或者更多影像中出现，所以要在多幅影像中选择建筑物重建最优纹理。不管是顶面或者侧面纹理选择，都要在建筑物某个纹理可见时，纹理区域面积越大，那么重建纹理图像就会越清晰，能够将建筑物表面纹理特征展现出来。

3.实验结果

本文实现无人机系统数据的实验，提供实验数据无人机系统包括环境调查、资源调查、灾害测量系统，使用不同小型固定翼无人机飞行平台，无人机飞行高度为200-2000m，无人机平台挂载定位精度为5-15m左右动态单点定位GPS与定位10°之内陀螺仪。飞行前通过航线规划软件设置拍摄重叠与旁向重叠，避免图像模糊，相机曝光时间不超过1/500s。

3.1 实验结果

本文实现Bundler中GPU并行化，对比增量式重建方法与批处理方法标定结构差异，给出实验数据，一组数据包括通过专业摄影测量软件Inpho标定结果，将此结果作为参考，使批处理方法实验结果对比。

对比Inpho测量软件，数据共有2037 幅图像，飞行高度为1000m，数据辅助部分（如表1 所示）。对比结果（如图3 所示）。本文绝对定向使用方法为标定位置信息与辅助信息GPS 位置信息绝对定向，所以GPS 位置信息具有误差。图3表示批处理方法标定结果与Inpho 标定结果差距为10m，此记录GPS 坐标精度相当，所以标定结果处于合理误差范围。

表1 数据辅助部分

图3 对比结果

对相机位置信息各分量进行统计，方向角信息各分量误差均值、最大值、外点个数与90%误差范围进行统计。对比结果（如表2 所示）：外点信息指的是误差超过均值误差5 倍的误差个数，90%误差范围指的是90%误差中最大误差值。本组数据在CPU版本运行时间在10 天以上，此数据在使用CPU版本运行中出错，标定过程中出现中断，结果出现严重错误。推测主要是因为增加某幅图像位置估计优化过程中出现错误，从而在添加后续图像的时候整体结构出现错误。GPU版本中Bundler，因为显存原因，在捆绑调整时无法通过，简单来说此实验使用增量式重建方法标定。处理此数据合理方法就是实现原始数据分组调整，使增量式重建方法改变成为分步重建思路。

表2 对比结果

3.2 结果分析

批处理方法和增量式重建对比，在大数据无人机图像处理能管理方面有所提高，并且此摄影软件Inpho标定结果对比，整体精度处于10m之内。根据GPS坐标绝对定向，GPS坐标自身具有10m误差，所以批处理标定结果在合理标定范围中。此数据表示，在无人机图像摄像机投影矩阵估计与场景重建过程中，批处理方法对比重建Bundler方法在处理效率、能力和稳定性方面具有一定优势，本文算法在无人机图像重建和标定过程中具备可行性[9]。标定结果位置与角度误差统计结果（如表3 所示）：

表3 标定结果位置与角度误差统计结果

4.结束语

本文提出了三维重建无人机影像全自动拼接方法，此方法通过密集点云方式重建拍摄区域，并且不需要其他的辅助数据，在拼接过程中不需要人工干预。通过实验结果表示，无人机影像全自动拼接方法能够及时得到高精度拼接影像。本文算法能够过滤显著离散点，但是对边缘点误认为离散点过滤，对拼接精度造成影响。因为拼接数据为高光谱影响，本文不对拼接辐射一致性问题考虑，上述问题在后续研究过程中改进。