液氮超声空化CFD模拟及实验研究

石珊珊，魏爱博，张小斌

（浙江大学制冷与低温研究所，浙江杭州310027）

引 言

与传统的水力空化[1]有所不同，超声空化是基于超声波激发的主动空化现象，是一种发生在液体中的强声现象，几乎所有液体中的强声技术都和声空化有关[2]。超声空化发生机理为：液体中的微小泡核在超声波作用下被激活，随着声波的稀疏相和压缩相生长收缩多次振荡，最后以高速崩溃。由于气泡的非线性振动和它们破灭时产生的巨大压力，伴随着这种空化现象会产生许多物理和化学效应[3]，在许多领域中都能起到积极作用。

超声空化的优点在于能够将声能集中在小体积中，将声学转换为伴随高温和高压的极限物理[4-5]，从而激发一连串物理、化学等方面的特殊性质，使得该效应表现出潜在的巨大理论和应用价值，近年来对水作为工质的超声空化研究取得了较大进展。Lee 等[6]使用脉冲超声的声学技术成功获得测量水中声致发光气泡大小的新方法。朱昌平等[7]分别使用荧光法、碘释放法和电学法对双频超声辐照系统的空化增强效应进行了研究。刘亚楠等[8]采用脉冲激光照明和长距离显微技术，并利用图像识别技术获得气泡半径在外界压力作用下的变化曲线。孙冰[9]利用Fluent 对超声空蚀仪振动的流场进行了模拟分析，研究了超声振动相关参数对空化的影响机理。Žnidarčič 等[10]提出了一种改进的超声空化建模，计算所得腔体界面动力特性、腔体积和排放压力等与实验有很好的一致性。Petkovšek等[11]通过光动力实验装置对空化气泡和声波的传播进行了分析，由光速偏转探测信号来决定声波和空化气泡。

由于低温条件下液体空化过程中热效应的影响不可忽略，因此呈现更加丰富的物理机理。不少研究者搭建了低温条件下的空化实验台对低温空化进行观测[12-15]，也有不少研究者利用CFD 方法对低温空化进行模拟计算[16-19]，获得了与常温流体空化相比不同的机理特性。对于低温流体超声空化的研究则较少，Dular 等[20]利用超声波发生器在液氮中产生空化，测量了金属样品的腐蚀情况，并与低温和高温水中的测试结果以及其他工程材料的损伤结果进行了比较，实验中发现液氮中的空化作用比水中的空化程度要小得多，而热水和冷水中的空化对金属侵蚀性相当。对于空化腐蚀问题的情况，缺乏实验及数值计算数据的情况依旧十分明显，在严格的压力控制和空化程度及其动力学的控制情况下，低温流体中的材料侵蚀特性研究则更少。本文利用Fluent18.1 软件进行数值计算分析，研究超声波发生器在液氮中的空化机理及特性，并与实验结果进行对比分析。

1 数值模型

1.1 控制方程

对液氮超声空化的数值建模基于Mixture 多相流模型[21]。该模型求解气液两相混合物的Navier-Stokes 方程，通过滑移速度来考虑两相相对速度，控制方程如下。

连续性方程

动量方程

能量方程

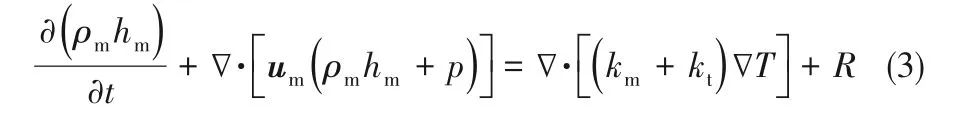
式中，ρm为气液混合相的平均密度，kg/m3；t 为时间，s；um为气液混合相的速度矢量，m/s；p为压力，Pa；μm为层流动力黏度，Pa·s；μt为湍流动力黏度，Pa·s；F 为体积力，N/m3；hm为气液混合相的平均焓值，J/kg；km为层流热热导率，W/(m·K)；kt为湍流热导率，W/(m·K)；T 为温度，K；R 为相变引起的能量源项，W/m3。混合相物性基于体积含量α 权重得到，以密度为例：ρm=αvρv+(1-αv)ρl。

假设流体可压缩，考虑流体的黏性和湍流，则气液两相空化流的质量输运方程[22]为

式中，fv为气相质量分数；Re和Rc分别为气相产生率和液化率，kg/(m3·s)，其值由完全空化模型计算得到，如式(5)、式（6）所示。该模型由Singhal 等[23]在Rayleigh-Plesset 方程的基础上推导得到，考虑了不凝结气体的影响。

当p ≤psat时

当p ＞psat时

式中，psat为饱和蒸气压，Pa；Ce和Cc为经验常数，m/s；ρv为气体密度，kg/m3；ρl为液体密度，kg/m3；σ为气泡表面张力，N/m；K 为湍流动能，m2/s2；pv为临界饱和压力，Pa。湍流特性基于Realizable k-ε 模型计算。

1.2 计算模型

建模的二维几何模型如图1 所示，腔体高度为170 mm，宽度为150 mm，模拟的超声波发生器插入腔体内部，端面与腔体底部距离为150 mm，基于Moving wall的运动来模拟发生器的高频振动。所有壁面均为无滑移壁面，容器顶端为压力出口，设定系统压力为100 kPa。

利用CFD 计算前处理软件Gambit 3.2 生成网格，为适应动网格方法，选择非结构化网格对计算域进行网格划分。在求解前先进行网格无关性验证，网格数最终确定为46124 个，网格质量高于0.99。在计算过程中由于运动壁面附近网格的产生和消失，会导致网格总数的变化，经验证基本可认为对计算结果无影响。

1.3 求解方案

根据REFPROPv9.0[24]的数据，将液态氮和气态氮的热力学性质（如饱和蒸气压、密度、比热容、热导率和黏度）指定为温度函数。

由Žnidarčič 等[25]的研究可知，在发生超声空化时，并不是液体中的负压声场导致成核，而是换能器表面的高频运动，假设表面以正弦方式进行振荡，频率为20 kHz，振幅为164 μm，壁面运动规律为y=A×sin（2πft）。

使用Fluent软件求解控制方程。为获得更高的抗干扰性和更好的收敛性，采用速度-压力耦合求解（coupled）方案，梯度离散采用least squares cell based 方法，压力离散采用PRESTO!方法，气相质量分数方程的离散采用QUICK 方法，密度、动量、能量及湍流项离散均采用second order upwind 方法。收敛准则是气相输送方程、质量守恒方程、动量守恒方程的残差均低于10-3，能量守恒方程的残差低于10-6。

2 实验研究

搭建的超声波空化实验台如图2 所示，主要由可视化液氮超声空化装置及超声波发生器组成。空化装置真空密封，侧面有6个可视化窗口，底面有1 个可视化窗口。超声波发生器主要由压电式换能器及控制器组成，换能器工作频率为20 kHz，功率为1000 W，振幅/功率在50%～100%可调。换能器通过转化驱动电源端的高功率信号为机械振动[26-27]。实验中，液氮浸没超声波发生器的工具头3～5 cm，并基于高速摄像仪观察液氮空化过程。高速摄像仪记录频率为1000 fps，曝光时间为0.02 μs。

图1 计算域简化模型及监测点坐标Fig.1 Simplified model of computational domain and monitoring point coordinates

图2 可视化液氮超声空化实验装置及超声波发生器Fig.2 Visualized liquid nitrogen ultrasonic cavitation experiment set-up and ultrasonic generator

图3 给出了功率900 W，压力为0.1 MPa 时液氮超声空化发生前后的非稳态变化图像。实验开始前，振子周围无气泡产生，在图中标记为0时刻。发生空化后振子下方和两侧都产生了大量的气泡，振子附近存在面积较大的空化群，且空化群覆盖了整个振子，但受到观察窗可视化面积的限制，部分气泡无法观测到。

通过改变超声波发生器的功率改变振子的振幅。将超声功率降至500 W，得到振子周围流场的气泡分布情况如图4 所示。此时空化仍旧发生，但相对图3 流场中气泡数量明显减少，然而分布位置一样，主要分布在振子表面和两侧。

3 结果与讨论

3.1 模拟结果对比分析

超声波发生频率为20 kHz，振幅为164 μm，试样表面正弦运动的周期为50 μs，迭代时间步长取周期的1/100，即5×10-7s 进行数值计算。对于振动的试样表面（即图1 中的Moving wall）的物性参数，取面积加权平均值获得平均压力、平均温度和平均气相含量的变化曲线如图5所示。

图3 振子附近液氮空化的非稳态变化（f=20 kHz,p=101325 Pa,power=900 W）Fig.3 Dynamic distribution of liquid nitrogen cavitation near oscillator

图4 振子附近液氮气泡分布（f=2 kHz,p=101325 Pa,power=500 W）Fig.4 Liquid nitrogen bubble distribution near oscillator

从图5 可以看出，试样表面的绝对压力和气相含量均呈周期性变化，变化周期均与超声波发生器的振动周期相同。周期之间的压力曲线变化并不完全一致，这是由于压力波在壁面反射，与下一个压力波相互叠加，从而对流场产生影响[9]。压力的最大值达到0.85 MPa，最低值则小于液氮78.3 K 对应的饱和蒸气压0.113 MPa。平均气相含量随着绝对压力的变化也产生了相应的周期性变化，两者相位相差180°，即压力最大时气相含量最小，但不等于零，压力最小时气相含量最大，最大气相含量约为0.65。在计算的时间内温度整体呈下降趋势，下降幅度为1.2 K左右，但在每一个周期内均有较小幅度的波动。

图5 试样表面的平均压力、气相含量及温度变化曲线Fig.5 Average pressure,gas content and temperature change curve of sample surface

图6 振子附近气相含量分布非稳态变化Fig.6 Dynamic distribution of gas content near oscillator

图6给出了两个周期内振子附近气相含量的云图。第一个图50 μs 是指振子从t=0 时刻开始起振，到第一个周期结束（也是第二个周期开始）时间为50 μs，与图5 所示时刻一致。由图6 可知液氮超声空化发生在振子附近，与图3 所示的实验结果进行对比，空化群的产生区域和覆盖范围等现象，在结果上具有较好的一致性。同时数值计算弥补了实验条件的不足，完整地呈现了空化群在一个周期内经历的生长、断裂、消减等过程，其形状接近于哑铃状，即振子中心下方分布最窄，两侧近似对称且变大，覆盖面超过振子面积。一个有趣的现象是，虽然一个周期内压力呈周期变化，但是振子周围空化群面积的变化相对较小，由图5 可知，约70 μs 时流场中振子表面平均压力处于最高值附近，50 μs 和100 μs时振子表面平均压力最小，但从图6 来看，不同时刻的空化群覆盖面积几乎相等，不同的是空化群内的气相含量大小。

根据流场内气相含量分布情况，在振子下方流场中取出典型监测点P1～P4，其具体位置如图1 所示，其中P1 和P2 位于振子附近，始终被空化群覆盖，P3稍稍远离振子，部分时间被空化群覆盖，P4则远离空化群。图7给出了各点压力和温度随时间变化曲线，发现空化群覆盖区压力呈周期性变化，与振子运动周期一致，距离振子越近则压力振幅越大，相应的温度波动幅度也越大。而在空化群外压力没有呈现周期性，变化幅度也随着与振子距离的增加而变小。一个有意思的现象是，不管是在空化群内还是空化群外，当地温度都没有呈现与压力匹配的周期性振荡，而是振荡下降，且下降过程中非稳态变化似乎没有规律性。对于P4点，由于相对远离振子，振子的运动对当地的流场已经几乎没有影响。温度变化没有呈现周期性的原因可定性解释为，由于热容的存在会延迟温度变化，且导热速度较慢，是与复杂的相变换热及热力学行为耦合的共同结果。另外，从图7中可以发现，虽然振子为正弦规律运动，但是振子附近（P1 点）的压力并没有相应的按照正弦形式变化，这是由于压力低于当地温度对应的饱和压力时，诱导了空化的发生，蒸发的气体平衡了外加压力的下降，使得当地保持饱和压力。

图7 监测点压力（实线）和温度（虚线）变化曲线Fig.7 Pressure(solid line)and temperature(dashed line)change curve of monitoring points

Žnidarčič 等[10]对相同振子直径及相同频率的超声波发生器在水中的空化动力学进行了系统实验研究和数值计算，观察到振子下方呈现一个延展的空化群，在其下方则可以看到离散的气泡。对比图6 的液氮结果，发现类似的是，超空泡均发生在超声振子附近，这很容易理解，因为距离振子越近超声能量越大，而且空泡群覆盖面积同样大于振子面积。另外，每个周期之间对应时间的空化群形态都不完全一致，一个周期内空化群不会完全消失。不同的地方是，水空化群呈现中间覆盖面积大，两边面积小的结构，类似于橄榄球，而液氮空化呈现哑铃形结构。液氮和水的超声空化特性的不同，主要是由于两者的物性存在差异，液氮空化区存在显著的温降，这种由于温降导致的独有的特性称为热效应[28]。

3.2 不同参数的影响

改变振子的振幅，计算得到气相含量分布变化情况如图8所示，当系统压力、超声频率等条件一定时，振幅越大，空化群面积越大，且对比明显。当振幅只有50 μm 时，流场内不再出现较大面积的空化群，只在振子表面和两侧有极少量的气泡，这也与实验结果吻合(图4)，当超声波功率较小即振幅减小时，观察到的气泡数量大大降低。

图8 不同振幅流场气相含量分布变化情况（p=100 kPa，f=20 kHz）Fig.8 Distribution of gas content at different vibrator amplitudes(p=100 kPa,f=20 kHz)

图9 不同频率流场气相含量分布变化情况（p=100 kPa，A=100 μm）Fig.9 Distribution of gas content at different vibrator frequencies(p=100 kPa,A=100 μm)

图10 不同系统压力流场气相含量分布变化情况（f=20 kHz，A=100 μm）Fig.10 Distribution of gas content at different ambient pressures(f=20 kHz,A=100 μm)

数值计算中还可改变超声频率，系统压力等条件，来观察各参数对液氮超声空化的影响特性。改变超声频率和系统压力，模拟计算得到气相含量分布变化情况分别如图9 和图10 所示。当系统压力、振幅等条件一定时，超声频率越高，振子下方的空化群覆盖面积越大，气相含量越高。当超声频率、振幅等条件一定时，系统压力越高，空化群面积越小，当系统压力为105 kPa 时，振子下方仅出现较小的空化群，当系统压力为110 kPa 时，仅在振子表面有极少量的气泡。

通常会选择空化数来描述不同空化流动的动态相似，水力空化数[29]的表达式一般为

式中，σ 为空化数；p 为系统压力，Pa；pv为蒸气压力，Pa；ρ 为液体密度，kg/m3；v 为速度，m/s。对于超声空化，空化数仍需包括实现蒸发所需的能量潜力（p-pv）和超声波发生器提供的能量，以上参数都易确定，而对于速度，可选用超声波发生器的平均速度或最大速度，与功率有关，本文选用振子的最大速度v=2πfA，则式（7）可演变为

式中，f 为频率，Hz；A 为振幅，m。结合图8～图10 可知，空化数越小越容易发生空化，且产生的空化群面积越大，反之不易发生空化，空化群面积相对也较小。当空化数较小时，产生的空化群较大，不同工况结果相差较小且形状相似；但当空化数大于某一个数值时，振子下方不再出现大空化群，而是仅在表面出现离散的气泡。

4 结 论

本文采用Mixture多相流模型，Singhal空化模型和Realizable k-ε 湍流模型，通过动网格方法实现3mm 试样正弦形式振荡，模拟超声空化在液氮中产生空化区，获得振子周围流场温度、压力和气相含量分布演变，得到如下结论。

（1）振子附近气相含量分布非稳态变化存在一定规律。可观察到流场内存在明显的空化群，其产生区域和覆盖范围与实验结果有较好的一致性，且数值计算弥补了实验条件的不足，呈现了空化群的周期性生长、断裂、消减等过程，空化群形状接近于哑铃状。

（2）液氮超声空化区压力和温度等参数呈现周期性变化。振子表面的平均压力和气相含量呈周期性变化，且两者相位相差180°，温度的变化没有明显的周期性，但存在小幅波动，整体呈下降趋势。空化区内各点的压力同样呈周期性变化，离振子越近则压力振幅越大，相应的温度波动幅度也越大。相比于水中的超声空化，有相似的地方也有不同，不同的主要原因是两者的物性差异，液氮空化区存在明显的热效应特性。

（3）振子振幅、超声频率和系统压力等相关参数对液氮超声空化特性有一定影响。实验中获得了不同振幅对空化的影响特性，通过数值计算对此进行验证，同时还获得了不同超声频率和系统压力对空化的影响特性。提出了超声波诱导的空化数表达式，描述不同参数对空化流动的影响，结果证明空化数越小越容易发生空化，且所产生空化群的面积越大。

（4）本文的实验研究还存在不足之处，后续的工作可从空化区温度等参数的定量测量等方面开展，进一步验证数值计算的准确性，完善液氮超声空化机理的研究。