不同种类超临界流体异质结构及相变分析

王艳，徐进良，2，李文

（1 华北电力大学低品位能源多相流与传热北京市重点实验室，北京102206； 2 华北电力大学电站能量传递转化与系统

教育部重点实验室，北京102206）

引 言

超临界流体(supercritical fluids,SCFs)是指温度和压力均高于临界点的流体，同一个压力下的SCFs，其物性参数随温度的变化非常剧烈[1]，随着对物性的特殊性及相关优势不断认识，SCFs 技术在萃取、干燥、沉淀及煤、天然气、核能和太阳能等一次能源驱动的发电系统等工业生产中得到广泛的应用[2-3]。有学者认为在超临界区，液体和气体的两相界面消失，流体呈现单相状态[4]，但越来越多的学者通过实验和模拟手段证明SCFs 密度的异质特性。Arai等[5]采用小角度X 射线散射的方法，根据密度涨落和相关长度两个参数从微观和宏观尺度上定量、直接描述了SCF 的不均匀性。Cabaço 等[6]采用拉曼散射的方法证明了密度不均性不仅存在于SCFs 的溶液中，在纯SCFs 中同样存在。Yoshii 等[7]对沿1.07Tc(Tc为临界温度)等温线，密度在ρc/8～2.78ρc（ρc为临界密度）范围内的Lennard-Jones(LJ)流体Xe 进行计算，临界密度以下，径向分布函数(radial distribution function,RDF)第一峰值的位置几乎是恒定的，临界密度以上，第一峰值的位置随着密度的增大而减小；在不同的流体密度中，均能产生团簇结构，在临界密度处发现清楚的原子簇聚集，显示出较大的空隙。Metatla 等[8]对400℃，密度为0.17、0.31 和0.55 g/cm3的三维超(近)临界H2O 进行模拟，发现流体存在高、低密度区的异质结构，在氢键的作用下，低密度比高密度工况产生更强的异质结构。Skarmoutsos 等[9-10]对沿等温线1.03Tc，密度在0.2ρc～2.0ρc范 围 内 的 超 临 界 水(supercritical water,SCW)模拟计算，结果显示，存在很大的局部密度增强效应，密度增强效应和平均密度之间存在较强的依赖关系，由于氢键的存在，在平均密度达到1.6ρc时，密度增强现象依然存在；此外，对T=666 K，密度在0.0644 ～0.644 g/cm3的SCW 中局部密度结构和密度不均匀性的相互作用进行研究，发现与非氢键流体相比，氢键流体具有更强的密度增强效应，参数在0.6ρc～0.8ρc范围内得到最大值，并指出类气(gaslike, GL)流体是由一些孤立的小团簇组成，类液(liquid-like,LL)流体类似于不均匀的多孔液体。

1964 年Bernal[11]提出SCFs 存在气液边界之后，相关研究得以展开。Gallo 等[12]通过实验和计算机模拟的结果，对温度范围为600～800 K，压力范围为150+25n bar(n=1,…,10)（1 bar=105Pa）的SCW 热力学性质进行研究，研究发现连接各热力学参数极大值的线，即Widom 线收敛于临界点。Raman 等[13]通过分析动力学模拟确定热力学响应函数的极值位置构成氧的Widom 线，研究发现这些响应函数的极值线在25 bar，温度15～20 K之间都重合在临界点附近，超过这个点等温压缩系数开始偏离。Simeoni等[14]采用非弹性X 射线，确定了超临界流体氩(supercritical argon,SCAr)中纳米声波在高压下的传播速度，研究揭示了跨越Widom 线存在急剧转变，证实超临界区存在LL 和GL 区。Banuti 等[15-16]采用理论和分子动力学模拟方法进一步证明超临界区可以划分为LL、GL和两相三个区域。

从现有文献报道来看目前对SCFs 异质结构的研究主要集中在较窄温压参数范围，对近临界区单一的SCF 进行研究，较高温压参数及不同流体之间的对比研究鲜有报道。不同压力下，物理团簇的定量分析及不同相转变机制的研究至今尚未见报道。本文根据局部密度的均方根误差、物理团簇、密度不均匀性及相变焓等方面对SCAr 和SCW 的异质结构特性和相变机制进行全面分析对比。研究得到不同种类SCFs的结构性质及不同相之间演化机制，从基础层面为SCFs的工业应用提供支撑。

1 物理模型及模拟过程

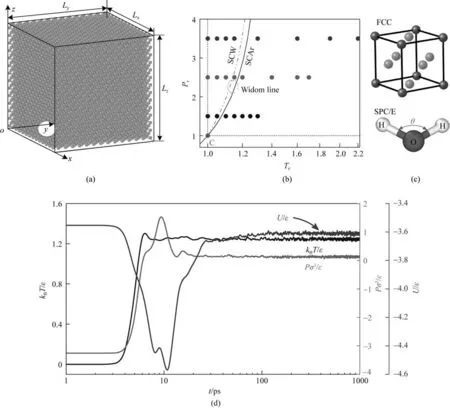
图1 模拟系统物理模型(a)；模拟工况Pr-Tr相图(b)；SCAr FCC结构和SCW SPC/E结构(c)；弛豫平衡过程温度、势能及压力随时间的变化规律(d)Fig.1 Physical model of simulation system(a);Simulation point on Pr-Tr phase diagram(b);FCC structure for SCAr and SPC/E structure for SCW(c);Variation of system temperature,potential energy,and pressure during relaxation and equilibrium stage(d)

SCAr 临界点温度、压力和密度分别为：Tc=150.687 K，Pc= 4.863 MPa，ρc= 0.52975 g/cm3。SCW临界点温度、压力和密度分别为：Tc=647.096 K，Pc=22.064 MPa，ρc=0.322 g/cm3。为了使得到的结果更具有普适性，对比分析不同种类SCFs 之间的关系，对压力和温度参数均进行无量纲化，则有Pr=P/Pc，Tr=T/Tc。为揭示不同性质SCFs 的结构特性，文中针对沿等压线Pr=1.5～3.5，温度范围为Tr=1.0～2.2 的SCFs 进行分子动力学模拟。模拟系统为立方体结构，即系统尺寸满足Lx=Ly=Lz=L，x、y 和z 三个方向均采用周期性边界条件。为保证SCFs的模拟精度，在各计算工况下模拟系统中需包含足够多的分子数，文中通过控制模拟体系的尺寸控制各工况系统内均包含10976 个SCAr 原子，7000 个SCW 分子，如图1(a)所示。图2(a)、(b)分别给出了SCAr、SCW 在不同压力下比定压热容(cp)随温度的变化规律，图中所有数据来自美国NIST(Standard Reference Database 23,Version 9.1)。由图可知，在临界压力以上时，cp存在一个最大值点，该点被称为拟临界点，对应的温度称为拟临界温度Tpc，不同压力对应着不同的拟临界点，随着压力的增大，拟临界温度升高，cp的最大值下降，且cp随温度的变化逐渐趋于平缓。不同压力cp最大值点的连线即为Widom 线，Widom 线两侧分布有LL 和GL 两个区域[14,17]。模拟主要包括Pr=1.5、2.5 和3.5 三个压力下较广温度范围内的若干工况，主要包括LL、GL 及拟临界点工况，在相图上的分布如图1(b)所示。

SCAr 采用面心立方(face-centered cubic, FCC)晶格方式排列，如图1(c)所示，文献[18-20]研究证实Lennard-Jones(LJ)势能模型对SCAr 仍然适用,得到的物性参数和NIST软件结果对比具有较高的精度，因此各原子之间的相互作用采用LJ势能模型，表达式为[21]：

式中，r 为氩原子之间的距离，氩原子间的尺寸参数σ = 0.3405 nm，能量参数ε = 1.67× 10-21J，原子质量m = 6.69 × 10-23g，模拟过程中势能截断半径为5.88σ(20 Å,1 Å=0.1 nm)[22]。

图2 Pr=1.5，2.5和3.5时SCAr和SCW的比定压热容和局部密度时序曲线的均方根误差随温度的变化Fig.2 Time evolution of specific heat capacity and the root mean square error of local density time series of SCAr and SCW at Pr=1.5,2.5 and 3.5

模拟过程中SCW 分子采用SPC/E 模型，该模型是MD 模拟中常用的扩展点电荷模型，可以比较精确地模拟高温高压下水的性质，适用范围较广[23]。在该模型中O—H的键长为1.0 Å，分子内两个O—H键之间的键角θ 为109.47°，如图1(c)所示。SCW 分子间的相互作用满足：

式(2)右侧第一项是在不同的分子间相互作用的LJ势，第二项是在不同分子上的i和j点电荷之间相互作用势能之和。ε0是真空介电常数，qi和qj分别是原子i 和j 的电荷，rij是两个不同分子上i 和j 原子间的非键距离，对于SCW 分子，仅考虑氧原子之间的能量和尺寸参数，则有ε=0.1553 kcal/mol（1cal=4.1868 J），σ =3.166 Å，电荷分别为：qO=-1.0484 C，qH=+0.5242 C。点电荷间的静电库仑力作用采用PPPM 方法计算，SCW 的几何构型使用SHAKE 算法进行固定，模拟过程中SCW 系统截断半径为9.5 Å[8]。模拟主要采用开源的分子动力学软件LAMMPS实现[24]，位型图后处理采用Ovito软件。

2 SCFs局部密度波动

为了观察给定温度和压力局部密度随时间的演化，通常对SCFs 模拟盒子沿z 方向中心厚约为10 Å 的局部区域区内的分子数进行统计，即可得到某一时刻该局部密度为：

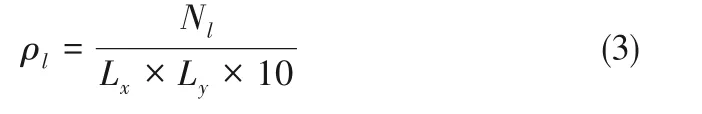
局部密度与系统平均密度的相对误差定义为：

均方根误差为：

式中，Nl为局部区域内分子数量，Lx和Ly分别为模拟盒子x 和y 方向的尺寸，ρave为系统平均密度，n是局部密度的样本总数。

根据上述方法可以得到不同压力局部密度时序曲线波动的均方根误差随温度的变化趋势，如图2(c)、(d)所示。在现有研究中提到在分子间短程作用力、临界波动和温度效应等的影响下[25-27]，对于SCAr，在Pr=1.5 和2.5 时 的 拟 临 界 温 度Tr,pc分 别 为1.075 和1.175，而密度波动均方根误差最大值对应的温度Tr,es分别为1.1 和1.2，与拟临界点温度Tr,pc的相对偏差分别为2.33%和2.13%。对于SCW，在Pr=1.5和2.5时的拟临界温度Tr,pc分别为1.058 和1.142，而此时密度波动均方根误差最大值对应的温度Tr,es仍为1.1和1.2，与拟临界点温度Tr,pc的相对偏差分别为3.97%和5.08%。随着压力的增加，当Pr=3.5 时，SCAr 的密度波动均方根误差最大值对应的温度Tr,es为1.9，与拟临界温度Tr,pc的相对偏差高达54.1%，但是随着压力继续增加，密度波动的均方根误差逐渐趋于一个水平线，峰值现象几乎消失。而该压力下SCW 的密度波动均方根误差最大值对应的温度Tr,es为1.4，与拟临界温度Tr,pc的相对偏差为17.0%。由以上可知，SCAr 和SCW 的均方根误差的最大值均出现在偏离拟临界点的工况，而后随着温度的升高逐渐降低，存在一个“脊”，与实验[6]中“脊”的位置偏离拟临界点，当热力学状态远离临界点时，偏离越大的结论基本一致。随着压力的增加，当Pr=3.5时，临界波动效应减弱，温度效应逐渐增强，均方根误差的最大值在偏离拟临界点较远的温度获得，SCAr随着温度的升高，该曲线逐渐趋向于平稳，而SCW则随着温度的升高呈微弱下降趋势。

3 结果与讨论

3.1 结构分析

3.1.1 物理团簇 为了研究不同种类SCFs 所形成的物理团簇，首先对给定压力，典型温度工况下流体的RDF 进行计算。RDF 是指局部密度与平均密度的比，得到的曲线是优先结构波动决定的。RDF的计算式为[28]：

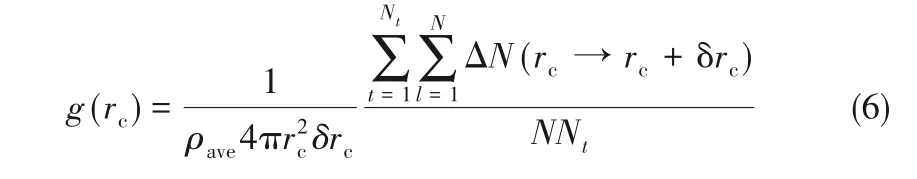
式中，N为分子的总数目，Nt为计算的总时间(步数)，δrc为设置的距离差，ΔN 为介于rc→rc+ δrc间的分子数目。

从微观角度来看，气态物质内部分子排列是完全混乱无序的随机结构，由于相互之间的距离很大，分子位置不固定，因此，气体无论在长程或近程上，都没有规律可言，气体的分子概括为“长程和近程都无序”。液体分子的排列既不像气态那样完全没有规律，也不像晶态那样具有强规律性，而是处于二者之间，在近程上有一定的排列特征，表现出“短程有序、长程无序”的典型结构排列规律[29-30]。当Pr=1.5时，SCAr和SCW 在LL、GL及类临界点温度的RDF 分布如图3 所示。由图可知，RDF 显示了预期的一般特征，在rc小时，RDF对温度的依赖关系并不明显。对于SCAr，RDF 的第一峰随着温度升高而降低，在Tr=1.0 的LL 工况，RDF 曲线具有明显的第二峰值和谷值，随温度的升高，在Tr=1.3 的GL 区，RDF 的第二个谷值和峰值几乎消失，这进一步说明，LL区具有“短程有序，长程无序”的结构特征，在高温下，短程有序的结构消失。对于SCW，由于分子间氢键的存在，氧-氧RDF 的第一峰随着温度升高而升高，第二峰值和谷值随温度的升高逐渐减弱，但是相较SCAr波动趋势较弱。同时说明不同性质的SCFs 随着温度的升高，分子的热运动加剧，系统内的熵增加，原子与原子之间的距离增大，结构变得疏散，“短程有序”规律消失。

以1.5σ 为目标范围对SCAr和SCW 物理团簇进行分析，凡是有连通效应的原子均属于同一个物理团簇。不同压力系统内的团簇个数和最大团簇原子数占比随温度的变化如图4所示。由图4(a)、(c)可知，在定压工况下，随着温度的升高，在一定温度区间内，系统内团簇数不发生变化，且压力越高，该温度区间越大，说明此时系统的密度较大，系统内大量原子组成一簇；温度继续升高，系统内团簇个数基本呈线性增加，压力越低，斜率越大。由图4(b)、(d)可知，最大团簇原子数的占比在低压较窄的温度区间，随着温度升高保持一个较大值，随压力增加，占比在较宽的温度范围内维持较大值；等温条件下，压力越高，最大团簇原子数占比越高。由此可以说明物理团簇的个数和最大团簇原子数的占比均是密度的函数，在高密度LL区存在较少的团簇数和较大的原子数占比，随着温度的升高或压力的降低，在低密度的GL 存在较多的团簇数和较小的原子数占比。根据该结论可以直观得到SCFs 在LL 区是一种连续的凝聚态介质，一个连续的网状分布被不同尺寸的孔洞打破；而GL 区是一种类似真空的团簇，系统中充满不同尺寸和异构体的团簇，和先前研究[10,31]的结论一致。

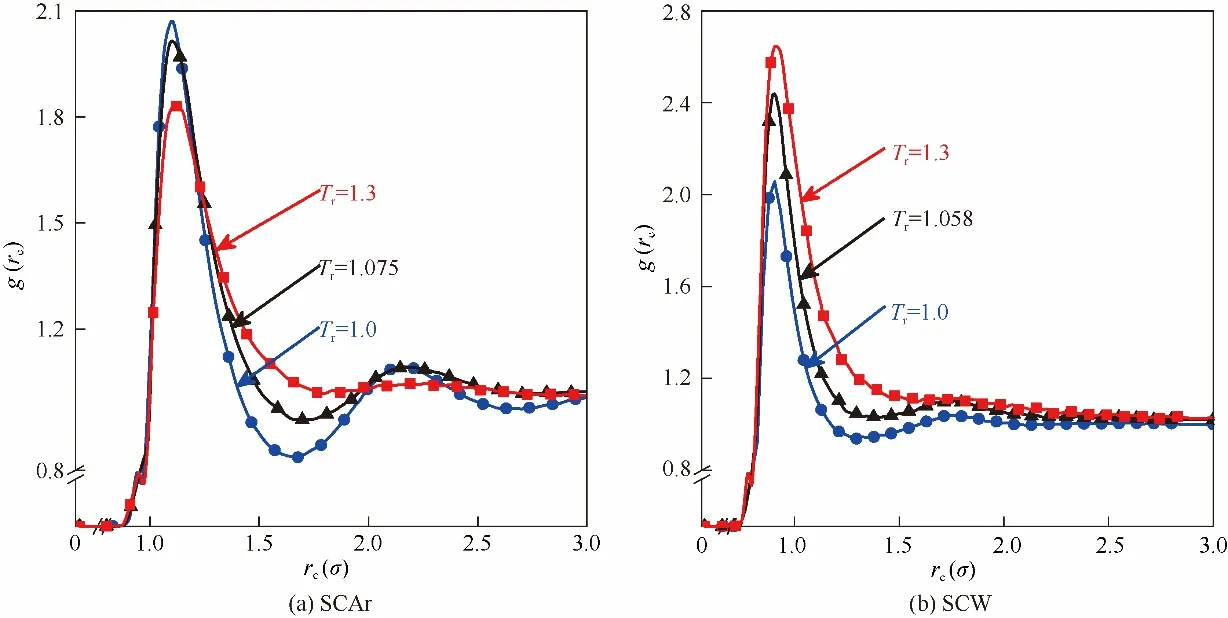
图3 Pr=1.5时SCAr和SCW不同温度下的径向分布函数Fig.3 The radial distribution functions of SCAr and SCW with different temperatures at Pr=1.5

图4 SCAr物理团簇个数随温度的变化(a)；SCAr最大团簇原子数占比随温度的变化(b)；SCW物理团簇个数随温度的变化(c)；SCW最大团簇分子数占比随温度的变化(d)Fig.4 The number of SCAr physical clusters varies with temperature(a);Proportion of SCAr atoms in physical cluster of the largest size under different temperature(b);The number of SCW physical clusters varies with temperature(c);Proportion of SCW molecules in physical cluster of the largest size under different temperature(d)

3.1.2 异质结构 配位数的变化趋势和密度呈线性关系，也是描述流体微观结构的重要物理参数，是距离目标分子为rx的球体内某种粒子的个数，可以用Nc表示，其计算公式[10]为:

在微观结构的表征中，配位数是用来描述中心分子第一壳层内分子的平均数目，反映的是中心分子与其他分子的结合能力和配位关系，描述体系中分子排列的紧密程度，配位数越大，分子排列越紧密。图5 给出了不同压力、不同温度(LL、拟临界点和GL)时两种SCFs配位数随积分距离变化的分布规律。由图可知，两种SCFs的配位数均随积分距离的增加而增大，随着温度的升高，增加的斜率逐渐减小，在给定压力工况，相同目标范围内，随着温度的升高，配位数减小；在给定温度工况，随着压力的增大，配位数增加。无论是在定压的低温工况或是定温的高压工况，均是由于系统密度的增大导致配位数的增加，进一步证明了配位数和密度之间的依赖关系。

图5 配位数Fig.5 Coordination number

SCFs 根据径向分布函数得到配位数计算值Nc，根据系统密度ρave，在相同的目标范围内计算得到配位数期望值Ne。通常认为对比两个值的大小即可得到系统内的高密度区和低密度区，当局部Nc＞Ne时，则该区域为高密度区，当局部Nc＜Ne时，则该区域为低密度区，当局部Nc=Ne时，则该区域为平均密度区。但是，在模拟过程中，分子结构的微小波动，则会导致局部区域所属密度特征发生变化，因此，提出一个稍微宽松的判断标准，即选取一个小量δ，用Ne± δ 作为参数度量平均密度的变化，具体划分原则如下：

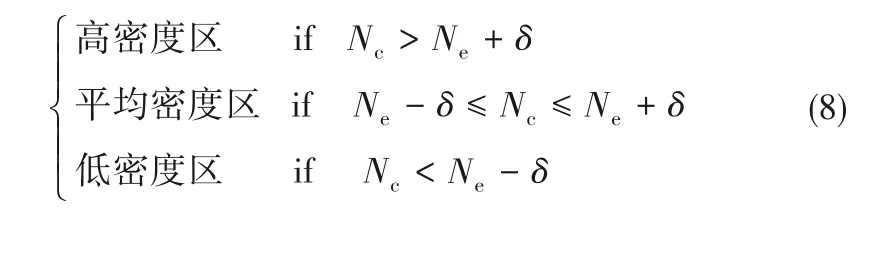
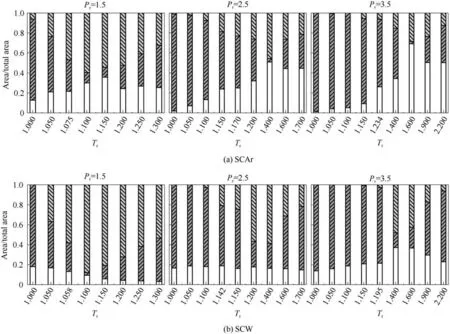
图6 Pr=1.5、2.5和3.5时系统内高密度区()、平均密度区()和低密度区(▭)的占比随温度的变化Fig.6 System density proportion of high density region(),average density region()and low density region(▭)varies with temperature at Pr=1.5，2.5 and 3.5

计算中允许的波动量为30%Ne，则δ 应满足2δ+1=0.3Ne，进一步得到不同参数下δ的具体值，利用划分原则可以判断密度分布趋势，称该方法为“30%方法”[32]。将模拟系统划分为若干小区域，计算可以得到每个区域在xy 平面内的配位数分布，采用式(8)的判断方法，将每个区域划分为高密度、平均密度和低密度区，分别计算不同温压工况各密度区的占比分布，具体如图6 所示。由图可知，不同压力下，两种SCFs不同密度区占比的整体变化趋势一致，平均密度区的占比随温度的升高呈现出“缩放喷管”的发展状态，即随着温度的升高，平均密度区的占比逐渐减小，在大于Tr,pc的温度时得到极小值，当温度进一步提高时，占比又逐渐增大。对于SCAr，在Pr=1.5 时，低温高密度工况表现为较强的均匀性，平均密度区占比的最大值约为81%，当Pr=3.5时，平均密度区占比达到99%。同时可以发现，在Pr=1.5时，高密度区占比随温度的增加逐渐升高，而后减小，该压力下低密度区的占比呈现出与高密度区占比相反的变化趋势。随着压力的增大，均匀性增加，在一定温度范围内，高密度区几乎消失，高密度区占比存在的温度区间仍表现为随温度升高先增大，而后减小的变化规律，此时低密度区占比随温度的升高而逐渐增大，在高温时逐渐趋于一个稳定值。对于SCW，在不同压力下，一定的温度范围内仍表现出较大的平均密度区占比，且随温度的升高，平均密度区占比在较宽的温度范围内都大于81%。存在高密度区的温度区间内，不同压力下高密度区占比呈现出随温度升高先增加而后减小的变化趋势。但不同压力下低密度区占比的变化趋势存在较大的差异，在Pr=1.5时，低密度区的占比随温度的升高逐渐减小，Pr=2.5 时，不同温度低密度区占比在一个较小的范围内波动，Pr=3.5 时，低密度区占比随温度的升高呈现出先减小后增大的变化规律。综上可知，SCFs 在近临界工况时表现出较强的异质结构特性，而随着压力的增大，工况点偏离临界点的程度增加，异质结构特性减弱，SCFs 表现为较强的均匀性。

3.2 平均力势分布

通常将PMF 定义为对系统所有构型施加的平均力势，通过其与密度的关系可以进行相关计算，则有[33]：

式中，ρz为位置z 处SCFs的密度。在Pr=1.5时，SCAr 和SCW 在LL、GL 和拟临界点工况xy 平面二维PMF云图如图7所示。由图可知，在给定压力下，不同温度的工况均表现出不同势阱深度的随机分布，根据式(9)，其中在较深的势阱处聚集了大量的分子，只有当动能足够大时，分子才能脱离势阱的束缚而移动。对比不同温度的势阱深度可以发现，随着温度的升高，势阱深度逐渐增大，即在GL 区势阱深度最大，LL 的势阱深度相对较小。主要因为GL 区温度较高，系统内分子动能较大，分子聚集则需要更大的势阱深度，不易形成大面积分子聚集现象；而LL 区分子间存在较强的相干性，较小的势阱深度即可引起分子聚集。在等温工况，提取局部不同势阱深度处的分子构型发现，在较大的势阱深度处对应较大的分子密度，随着势阱深度减小，分子逐渐变得稀疏。

图7 Pr=1.5时xy平面PMF二维云图分布及局部原子位型Fig.7 The PMF distribution over the xy plane at Pr=1.5

3.3 SCFs相变焓

文献指出可以将超临界区划分为LL、GL 和两相三个区域，三个区域的划分需要两个分界线，这两个温度分界可以根据文献[15]中提出的渐近线逼近理论方法进行求解，具体的计算过程如图8(a)所示，图中给出了SCAr 在压力Pr=1.5 时的i-T 图，对于给定的流体，在较大的压力范围内cp,l可以看作一个常数，表达式为：

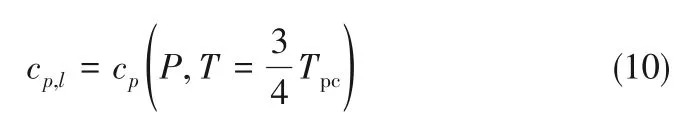
对于气相的cp,v，按理想气体处理：

式中，γ 为等熵指数，对于单原子惰性SCAr，γ=1.67，含氢键多原子SCW，γ=1.12；R=Rg/M，Rg是气体常数，值为8.3145 J/(mol·K)，M 为流体的摩尔质量，对于SCAr和SCW 其值分别为39.95 g/mol和18.00 g/mol。

图8(a)中三条线对应的方程分别为：

图8 理论方法确定两相区起止点温度(Pr=1.5,SCAr)(a)[15]；SCAr和SCW不同压力下焓随温度的变化及相变焓的确定[(b)、(c)]；SCAr和SCW相变焓随压力的变化规律(d)Fig.8 The start(Ts)and end temperature(Te)of two-phase region are determined by theoretical method(Pr=1.5,SCAr)(a);Variation of enthalpy with various temperature and the determination of phase change enthalpy under different pressures for SCAr and SCW[(b),(c)];The change of phase change enthalpy of different pressure for SCAr and SCW(d)

众所周知，亚临界工况属于等温相变，由液态到气态吸收的热量主要是汽化潜热。采用上述方法将SCFs 划分为三区，相变过程处于Ts和Te温度区间内，属于非等温相变过程。根据不同压力系统焓随温度的变化可以得到Ts和Te对应的焓值，从而确定LL 过渡到GL 所需要的焓值Δi，则称该值为SCFs的相变焓。SCAr 和SCW 不同压力的焓值随温度的变化如图8(b)、(c)所示。从图中可以得到，在给定压力时，随温度升高，焓值增大；给定温度时，随压力增大，焓值减小。在低温高密度区，焓值表现出对压力和温度的弱敏感性，各压力的焓值收缩在一个较小的范围内，在高温低密度区，则表现为较强的压力和温度的依赖性，焓值在较大空间内发散。随着压力的增大，曲线逐渐由二次变化向线性变化过渡，在Pr=3.5 时，具有较强的线性特性，同时压力增大，相变温度跨度增大，导致SCFs 相变焓增加。从图8(d)中可以得到两种SCFs 的相变焓均表现出随压力增大线性增加的变化趋势，SCAr 和SCW 的相变焓分别满足ΔiSCAr=55.48+18.19Pr和ΔiSCW=-87.76+679.96Pr的线性变化规律。

相变通常是系统内促使有序和无序的能量之间相互竞争的结果，分子间的相互作用导致有序，而热运动则导致无序。在温度升高的过程中，热运动逐渐加剧，将某种相互作用形成的有序性破坏，就可能出现新的相。从热力学的角度可以认为熵是系统混乱程度的一种度量方式，微尺度上熵可以看作分析无序的一种度量。当系统从无序到有序相转变时，系统熵的损失由更多的内能降低来补偿，当系统变得更无序时，分子的位置变得难以预测，熵就会增加。因此物质的熵在固相较低而在气相较高[34]，液体则处于二者之间。不同压力下，SCAr和SCW 的系统熵随温度的变化关系如图9 所示。由图可知，在等压工况时，两种SCFs 的系统熵随着温度的升高呈现两种变化规律，即低温高密度区和高温低密度区的线性变化，中温区的曲线变化，随着温度的升高，系统熵增大。在等温工况下，随着压力的增加，系统熵则呈现减小趋势。文献[35]指出对于同一种物质，在相同的压力下，熵的改变与温度有关，即满足：S=f(T)。综上可以得到随着温度的升高流体的无序度增大，温度降低无序度则减小。无论在何种压力，在低温高密度区，分子之间表现为较强的相干性，每个分子周围都和近邻分子形成簇，系统表现出较强的有序性。在高温低密度区分子间的相干性减弱或者消失，分子的运动是自由的，仅存在偶然出现的小团簇，系统有序性减弱。在等压工况下，随着温度的升高，密度减小，密度的减小导致系统内存在大量可用的未占据的区域，热运动的增大很容易导致熵增，引入无序，使系统演化为GL 状态。随着流体密度的增加，热运动产生的无序效应因几何或“排除体积”现象而逐渐减弱[36]，系统向LL状态演化。因此SCFs在熵驱动下完成LL-GL相变转换。

4 结 论

本文从局部密度均方根误差、物理团簇和配位数等方面对不同性质SCFs 的异质结构特性进行研究，同时根据理论计算获得三相转变的起止点温度，并对SCFs的非等温相变焓及相变作用机制进行分析，得到以下结论。

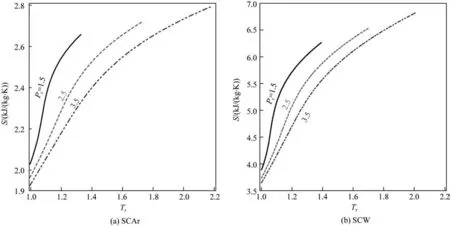
图9 不同压力下系统熵随温度的变化趋势Fig.9 Entropy at various temperatures and pressures

(1) 在近临界压力Pr=1.5 和2.5 时，局部密度波动时序曲线的均方根误差均在大于拟临界温度的位置得到最大值，存在明显的“脊”；当Pr=3.5 时，SCAr的均方根误差随着温度的升高，逐渐增大并趋于平稳，SCW 则在偏离拟临界温度较远的位置得到最大值，随后小幅度下降，但是在该压力下，两种SCFs的“脊”均减弱或消失。

(2)等压工况，不同温度RDF 的分布具有LL、两相和GL 的特征，峰谷的值随着温度的升高逐渐减弱，气相区在第一峰值后的峰谷均消失，表明流体“短程有序”特征消失。对各工况物理团簇进行分析发现，在等压工况，随着温度的升高，系统密度减小，团簇个数增加，最大团簇原子数占比降低，分别表现出低温区保持常数，随后线性增加或减小的变化趋势。在等温工况，随着压力的升高，系统密度增大，团簇个数减少，最大团簇原子数占比增加。说明低温高密度的LL区表现出连续介质性质，而高温低密度的GL 区则表现出真空介质性质。根据配位数大小可以将系统划分为低密度、平均密度和高密度区，在等压工况，平均密度区的占比随着温度的升高逐渐减小，而后增大。不同压力均在大于拟临界温度的工况得到平均密度区占比的最小值，且随着压力的增加，系统的均匀性增强。

(3) 采用理论方法，得到不同压力SCAr 和SCW两相区的起止温度Ts和Te，根据两温度对应的焓值差得到SCFs 的相变焓。结果表明，随着压力的增大，焓值曲线随温度的变化逐渐从二次分布演化为线性分布，相变温度跨度增大，相变焓增加，两种SCFs 的相变焓随着压力的增大均表现为线性增加趋势。此外，通过阐述SCFs 在LL 和GL 区的有序性与熵之间的关系，得到熵是驱动SCFs相变的重要作用机制。