钢管混凝土框架支撑结构二阶效应直接分析*
赵根田,周伟,李补拴,李霈清
(内蒙古科技大学 土木工程学院,内蒙古 包头 014010)
钢管混凝土柱提供很好的轴向刚度和承载能力,支撑体系则可满足侧向刚度的要求,故有支撑的钢管混凝土柱框架结构是一种经济有效的抗震结构体系[1].
高层钢管混凝土框架支撑结构体系的高宽比普遍较大,而矩形钢管混凝土柱的截面相对较小[2],所以需要考虑二阶效应[3-5].二阶效应通常包括结构水平位移对竖向力的影响(P-Δ)和杆件挠度对轴力作用的效应(P-δ)[6].考虑二阶效应要进行非线性分析,但精确的非线性分析一般都很费时,因此现在普遍采用简化分析方法考虑二阶效应[7].近年来国内外学者针对二阶效应进行了大量研究.CHAN S L等[8]提出的二阶设计理论可直接分析钢结构和复合结构.CHIOREAN C G等[9]提出新的结构二阶效应分析的计算机方法,可对钢框架进行非线性非弹性分析.黄慧等[10]对《钢结构设计标准》(GB 50017—2017)与美国钢结构设计标准(ANSI/AISC360—10)的稳定性设计方法进行了对比,认为在进行钢结构设计时,结构稳定分析方法与构件设计须在一套规范体系内配套使用.就弹性材料而言,弯矩—曲率效应曲线呈线性变化趋势,刚性框架非线性仅由P-δ引起.对于超高层结构或高宽比较大的结构,P-Δ效应十分明显.但精确的二阶效应分析还需将P-δ考虑在内.《混凝土结构设计规范》(GB 50010—2010)规定:对结构进行非线性分析时,宜计入结构的几何非线性对作用效应的不利影响.《高层建筑混凝土结构技术规程》(JGJ3—2010)规定:高层结构在一定条件下,应考虑重力二阶效应对水平力作用下结构内力和位移的不利影响.
为探讨二阶效应对钢管混凝土框架中心支撑结构内力和变形的影响,本文以某高层中心支撑钢管混凝土框架住宅工程为例,通过设置假想水平力,引入结构和构件的初始几何缺陷以及残余应力影响,同时考虑P-Δ和P-δ二阶效应,对结构的内力和位移进行分析,并得出一些结论.
1 工程概况
本工程地处包头市青山区版块内,设计为G都城二期14号楼,共32个标准层,建筑顶标高95.700 m,采用矩形钢管混凝土柱-钢支撑组成的双重抗侧力结构体系.柱、梁和支撑均采用Q345钢材.柱子采用矩形钢管混凝土柱,从下到上柱子截面逐步收缩,1到18层的混凝土等级为C50,19层到屋面的混凝土等级为C45.支撑竖向布置见图1,一层和二层及三层和三层以上的柱及支撑布置见图2和图3,一层梁平面布置见图4.一层结构的柱、梁和支撑的截面编号、截面尺寸见表1.使用SAP2000软件进行三维建模,如图5所示.在分析过程中结构的梁、柱及支撑都选用空间杆系单元,楼板和屋面采用壳单元.框架柱底部与基础完全固接,忽略地下结构对上部的影响,框架梁与框架柱刚性连接,次梁则为铰接.建模时,底层支撑嵌入柱子,首层以上则嵌入梁,从而保证底层支撑的节点自由度被约束.
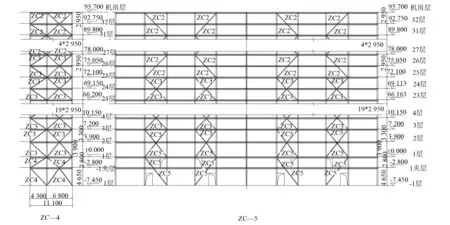
图1 支撑竖向布置图
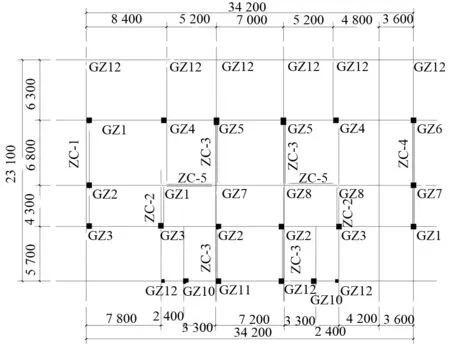
图2 一层和二层钢柱及支撑平面布置图
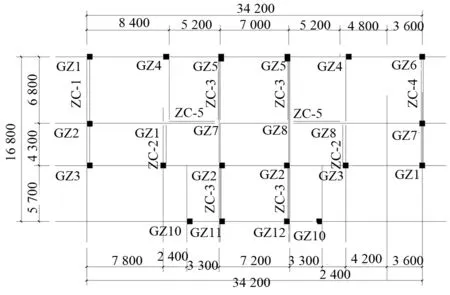
图3 三层及三层以上柱及支撑平面布置图

图4 一层梁平面布置图

表1 柱、梁及支撑截面尺寸(翼缘为火焰切边)

图5 三维建筑模型
2 荷载取值及其效应组合
楼板自重2.5 kN/m2,楼面荷载(不包括楼板自重)1.5 kN/m2,屋面荷载(不包括楼板自重)取2.0 kN/m2.楼面活荷2.0 kN/m2,屋面活荷2.0 kN/m2.抗震设防烈度6度,基本加速度0.10 g.基本风压(按50 a一遇)0.55 kN/m2.基本雪压(按50 a一遇)0.65 kN/m2,且屋面的雪荷载与活荷载不同时考虑.设计时,控制荷载主要是沿X,Y方向的风荷载效应.
墙体采用纤维水泥板(CCA)灌浆墙,灌浆材料为泡沫混凝土,墙体荷载采用线荷载计算,外墙厚280 mm,重度不大于1.85 kN/m2,分户墙厚150 mm,重度不大于1.65 kN/m2,分室墙75 mm厚,重度不大于1 kN/m2.
根据《建筑结构荷载规范》(GB 50009—2012)3.2.1条规定,按承载力极限状态和正常使用极限状态分别进行荷载组合,考虑永久荷载和可变荷载中屋面活载、风荷载起控制作用以及地震作用参与的影响,得出以下7种荷载效应组合:
(1)承载力极限状态下可变荷载中楼屋面活载起控制作用的工况;
(2)承载力极限状态下永久荷载起控制作用的工况;
(3)承载力极限状态下可变荷载中风荷载起控制作用的工况;
(4)正常使用极限状态下可变荷载中楼屋面活载起控制作用的工况;
(5)正常使用极限状态下可变荷载中风荷载起控制作用的工况;
(6)承载力极限状态下地震作用参与的组合工况;
(7)正常使用极限状态下地震作用参与的组合工况.
3 结构二阶效应弹性分析和直接分析
本工程使用SAP2000软件建模分析,分别考虑了结构的一阶分析、二阶弹性分析以及直接分析,并将结构的内力和位移计算结果进行对比分析.
对于二阶弹性分析可以忽略材料非线性的影响,但需要建立考虑结构体系形变的平衡方程,即考虑结构的几何非线性.根据《钢结构设计标准》(GB 50017—2017),计算得该结构X向二阶效应系数θ均大于0.1,且计算一阶分析时,结构在地震荷载作用下结构的层间位移角除了首层外其余各层都大于1/1000,在第18层出现了位移角的峰值1/391,因此本案例需考虑二阶效应.
二阶弹性分析应考虑二阶P-Δ效应还要考虑结构整体初始缺陷和构件初始缺陷、节点连接刚度和其它对结构稳定性有显著影响的因素.直接分析应考虑二阶P-Δ和P-δ(P-Δ-δ)效应,同时考虑结构和构件的初始缺陷、节点连接刚度和其他对结构稳定性有显著影响的因素.假设材料在弹性范围内,计算结构在各种设计荷载(作用)下的内力和位移.
3.1 结构初始缺陷
结构整体初始缺陷以结构第一阶屈曲模态为基础,考虑结构的层间位移得到;考虑初始缺陷时使其与最不利风荷载方向一致.初始缺陷通过在每层柱子的柱顶施加假想水平力实现.假想水平力计算结果如表2所示.
根据《钢结构设计标准》(GB 50017—2017)5.2条,表2中各层假想水平力由式(1)计算所得:
(1)

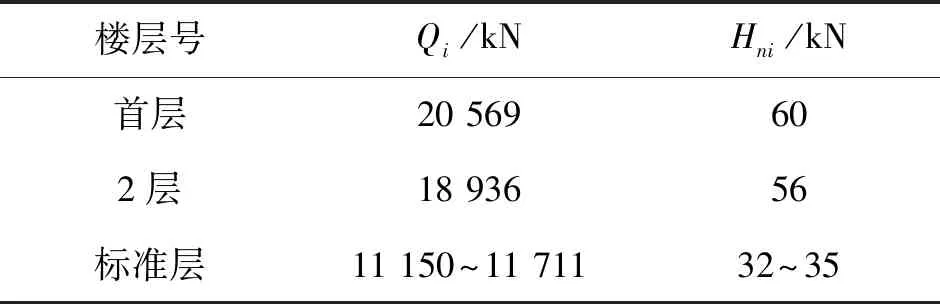
表2 各层假想水平力
3.2 各层框架柱及支撑的初始缺陷
构件的初始缺陷和残余应力可以由杆件的初始弯曲即正弦曲线来确定,这些缺陷包含了支撑的缺陷.本工程的柱子稳定计算属于b类截面,弯曲缺陷e0/l(e0为构件中点处的初始变形,l为构件总长度).取1/350,构件长度取层高,框架柱假想分布力的大小和柱子的轴力标准值Nk成正比,在0.59 kN/m到2.97 kN/m之间,如表3所示.
不同的楼层同一位置的支撑截面不同,而同一楼层不同位置的支撑截面也不同.在同一楼层的相同位置由于交叉支撑有偏心而导致支撑的长度不一样,从而计算出的假想水平力也有差别.支撑的弯曲缺陷值e0/l取1/350,支撑的假想分布力在0.35~3.81 kN/m之间,由于26~33层的楼层刚度减弱,分配到的地震力较小,支撑所受的轴力较小,因此该段楼层的假想分布力较小,在0.35~0.79 kN/m之间,如表4所示.

表3 各层框架柱假想分布力
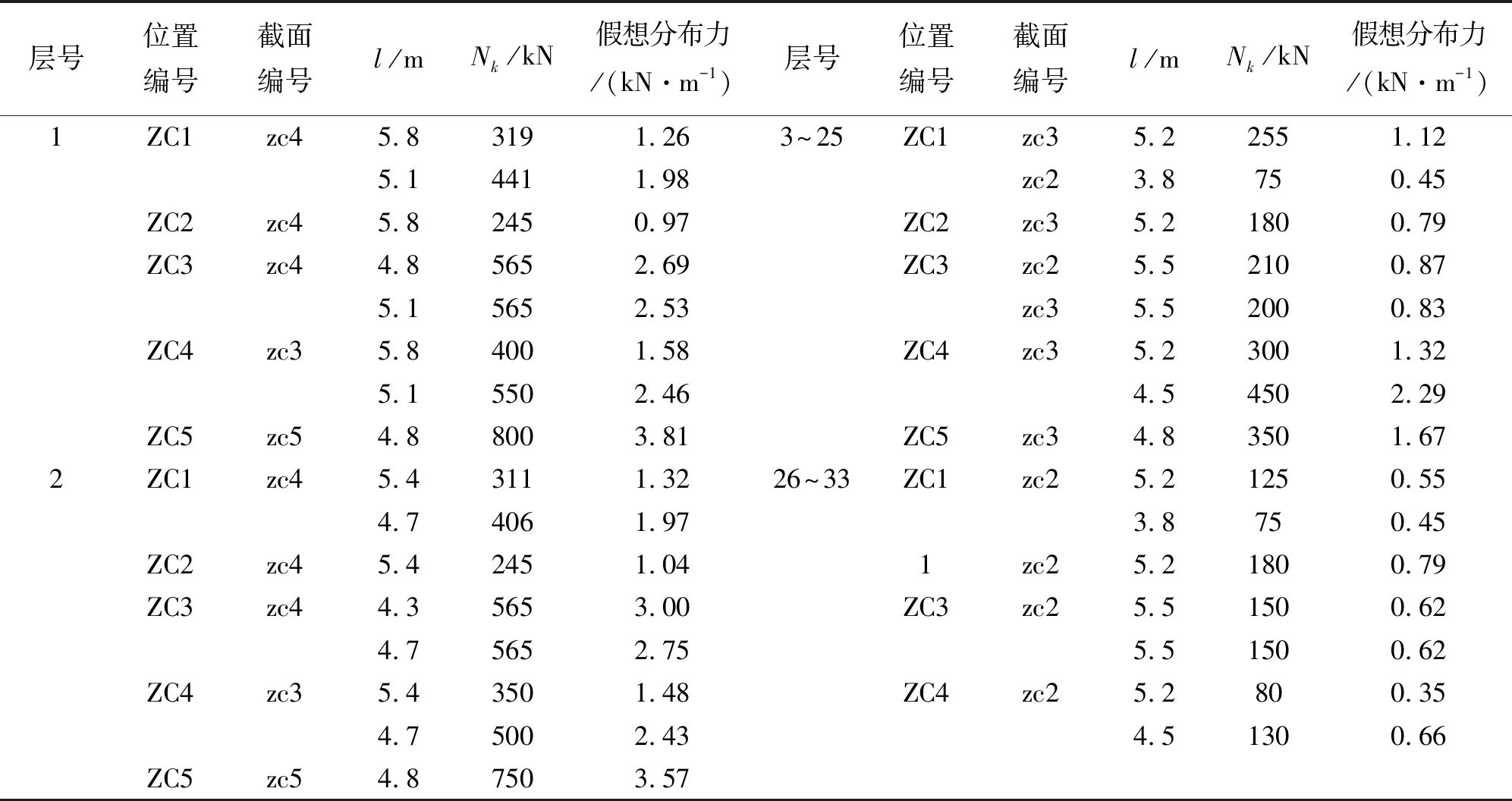
表4 各层支撑假想分布力
3.3 二阶效应弹性内力分析结果
将假想水平力施加到结构上进行二阶效应的分析.取图2中受力面积较大的15轴线的GZ3柱,GZ3与GZ9相连的梁,考虑水平风荷载起控制作用且风荷载和初始缺陷均沿X轴或Y轴方向,取工况5DWXLS进行分析.工况5DWXLS(正常使用极限状态下可变荷载中风荷载起控制作用的工况,其荷载组合系数为1.0D+1.0WX+0.7L+0.7S.D,WX,L,S分别表示可变荷载,沿X方向的风荷载,永久荷载和雪荷载)和5DWYLS(WY表示沿Y方向的风荷载)下一阶弹性分析、二阶弹性分析和直接分析内力及结果比较分别见表5,6.表中①为一阶弹性分析,②为仅考虑P-Δ效应的二阶弹性分析,③为考虑P-Δ-δ效应的直接分析.
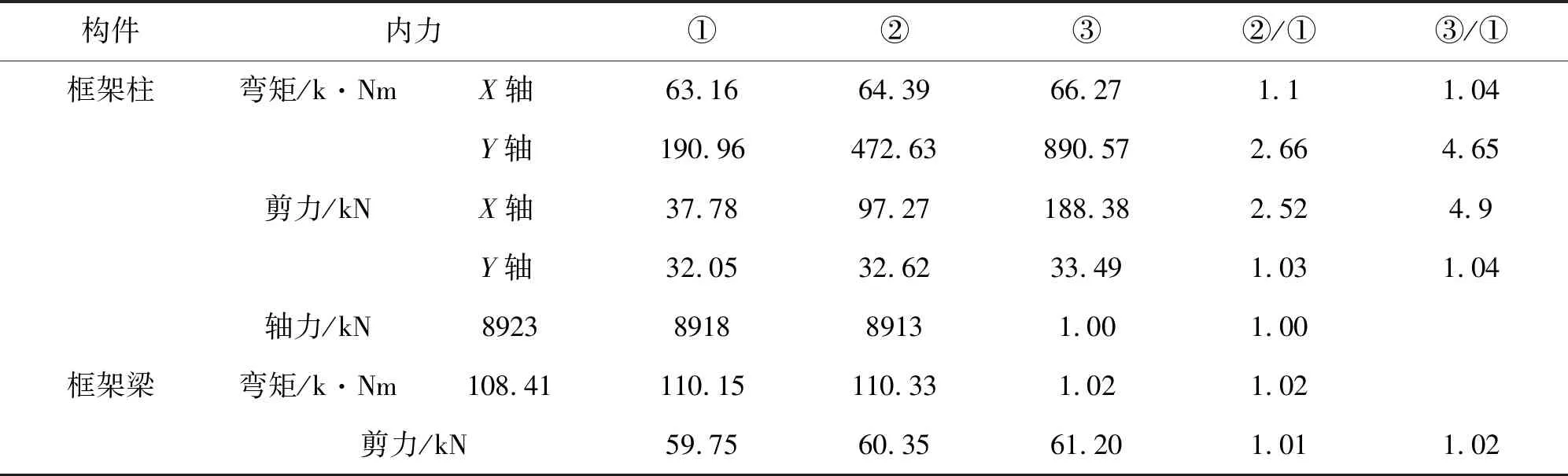
表5 一阶分析、二阶分析和直接分析内力对比(工况5DWXLS)

表6 一阶分析、二阶分析和直接分析内力对比(工况5DWYLS)
(1)只考虑效应的二阶弹性分析内力
根据表5,在工况5DWXLS下,框架柱绕X轴的二阶弯矩为一阶弯矩的1.1倍,绕Y轴的二阶弯矩为一阶弯矩的2.66倍,沿X轴向的二阶剪力为一阶剪力的2.52倍,而沿Y轴的二阶剪力与一阶剪力基本相等,再者二阶效应对柱子轴力影响可以忽略.二阶效应对梁的弯矩和剪力基本没有影响.
根据表6,荷载工况转变为5DWYLS,框架柱绕X轴的二阶弯矩为一阶弯矩的2.88倍,沿Y向的二阶剪力为一阶剪力的3.67倍.其余指标变化很小,都在5%以内.
只考虑P-Δ效应时,沿着假想力方向的柱剪力和绕与假想力垂直方向的柱弯矩影响较大,而对梁的内力影响在2%左右.
(2)考虑和P效应的直接分析内力
由表5在5DWXLS工况下,框架柱绕X方向的弯矩与沿Y向的剪力在考虑了P-Δ-δ效应后仅为一阶内力的1.04倍,几乎可忽略.而绕Y方向弯矩和沿X方向剪力分别是一阶内力的4.65倍和4.9倍,轴力几乎不变.框架梁的二阶效应使得内力增大了2%,可不考虑.
由表6在5DWYLS工况下,考虑了P-Δ-δ效应后绕Y方向弯矩和沿X方向的剪力分别是一阶内力的0.81和0.95,并不需要考虑其不利影响.但是同样的绕X方向的弯矩与沿Y向的剪力比一阶内力分别增大了2.6倍和3.8倍,轴力依旧不变.框架梁的二阶效应对其内力影响也可忽略.
考虑效应后,对沿着假想力方向的柱剪力和绕与假想力垂直方向的柱弯矩影响较大,而对梁的影响也在2%左右.
在5DWXLS工况下,在一阶内力基础上仅仅考虑P-Δ,使得绕Y轴的二阶弯矩和沿X向的二阶剪力分别增大了1.66倍和1.52倍,而在考虑了P-Δ效应的基础上再加上P-δ,则同样的内力又分别提高了94%和88%.5DWYLS工况下也有类似的结果.因此,P-Δ-δ效应对构件内力的增大效应非常明显.特别是对于轴力较大的构件,无论是效应还是效应都比较明显,且仅仅对沿着假想力方向的剪力和绕与假想力垂直方向的弯矩影响明显.
3.4 二阶弹性位移分析结果
(1)只考虑P-Δ效应的结构弹性位移二阶分析结果
结构一阶分析与二阶分析(仅考虑P-Δ)得到的层间位移比较见图6(工况5DWXLS和5DWYLS).层间位移和顶部最大位移见表7.

图6 考虑P-Δ效应的二阶与一阶层间位移的比较(a)X向;(b)Y向
表7在5DWXLS工况下,只考虑P-Δ效应的二阶层间位移与一阶层间位移的比值在1.93~2.54之间,底层和顶层分别取得最大值2.54和最小值1.93.二阶分析与一阶分析层间位移的变化趋势相同,都在16层取得层间位移峰值.只考虑P-Δ效应的二阶分析顶点位移是一阶分析的2.12倍.在5DWYLS工况下,只考虑P-Δ效应的二阶层间位移与一阶层间位移的比值在1.92~2.25之间,顶点位移的比值为1.95.结构刚度较大的1~5层,其层间位移比值的平均值为2.17,而由于柱子变截面使得刚度较小的27~32层层间位移的比值均值为1.93,相较于1~5层该比值下降了11.05%.
只考虑效应的二阶弹性分析的层间位移和顶点位移明显要大于一阶分析结果,结构在5DWXLS和5DWYLS工况下,只考虑P-Δ效应的二阶层间位移与一阶层间位移的比值的波动区间重合度很高,说明P-Δ效应对于不同工况下结构位移的影响相近,而且P-Δ效应对刚度大的楼层的位移增大效果要大于刚度弱的楼层,但提升效果不显著.
(2)考虑P-Δ和P-δ效应的结构弹性位移直接分析结果
结构一阶分析与直接分析(考虑P-Δ-δ)得到的层间位移比较见图7(工况5DWXLS和5DWYLS).层间位移和顶部最大位移见表7.
由表7看出:在5DWXLS的工况下,考虑P-Δ-δ效应的直接分析位移与一阶位移的比值在3.34~4.91之间,在第18层都取得位移峰值,分别为3.13 mm和11.63 mm.在5DWYLS工况下考虑P-Δ-δ效应的直接分析位移与一阶位移的比值在2.82~2.30之间,都在20层取得位移峰值,分别为5.68 mm和13.17 mm.
考虑P-Δ-δ效应的直接分析位移在1~8层增加十分明显,其增加的绝对位移是一阶位移增加量的2.31倍,位移变化明显,符合结构的最不利荷载组合原则.
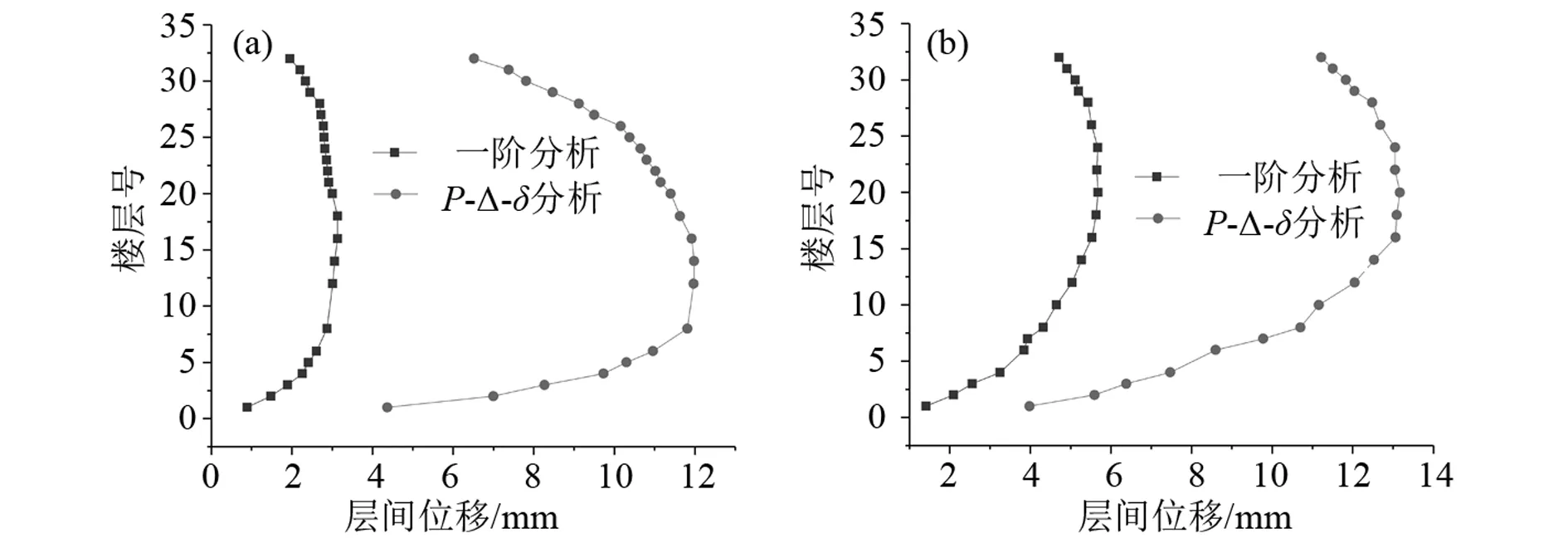
图7 考虑P-Δ-δ效应的直接分析与一阶层间位移的比较(a)X向;(b)Y向

表7 层间位移和顶部最大位移
由表7可以得出:
(1)在弹性状态下,仅仅考虑一阶分析的位移结果相对于二阶分析的位移结果小很多,表中所列二阶位移与一阶位移的比值都大于2.3.
(2)以5DWYLS工况下结构位移来说,一阶顶点位移150.4 mm,仅仅考虑P-Δ效应的顶点位移293.8 mm,同时考虑P-Δ-δ效应的顶点位移356.2 mm.仅考虑P-Δ效应的顶点位移比一阶顶点位移增加了95.4%,考虑P-Δ-δ效应的顶点位移比仅考虑效应的顶点位移又增加了21.2%.因此,整体缺陷引起的P-Δ对结构位移的增大幅度明显要高于构件缺陷对结构位移产生的增加幅度.
4 结论
在同时考虑结构的初始缺陷和构件缺陷的前提下,使用直接分析法对结构二阶效应进行弹性分析,经结果比较得出以下结论:
(1)整体缺陷加剧结构的P-Δ效应,产生的位移增量明显大于构件缺陷所产生的位移增量.
(2)考虑P-Δ-δ效应的框架柱弯矩要远大于只考虑P-Δ效应的柱弯矩,但对剪力和轴力影响不明显.对于轴力较大的柱,二阶效应的影响更为显著.
(3)对于复杂的高层钢框架支撑结构,P-Δ-δ效应增加的内力和位移值十分显著,设计时必须考虑.
——以明某某案为例

