论“平均安培力”快速解题的依据及可靠性

张 旭 农艳鸯

(柳州市第二中学 广西 柳州 545001)

1 引言

在高考中采用不同方法和手段分析、处理信息进而准确而又快速地解决问题是学生应该要掌握的科学思维．教师作为学生的引导者，在学生已经掌握的情况下，如何引导学生去探究发现一些快速可靠的解法也应该是广大中学物理教师的一门必修课．这里我们从2020年柳州市二模的一道选择题引入，讨论一下安培力在哪些情况下可以用“平均值法”解题．

图1 例1题图

D.右端电阻R产生的焦耳热为mgh

答案：A，C.

解：由题意得

故选项A对．

针对选项C，设导轨进入磁场速度为v，从静止释放到进入磁场前由动能定理有如下解法.

常规答案解法：

(1)

(2)

(3)

令

得

平均值解法：

(4)

(5)

得

2 讨论与证明

如图2所示，假设光滑导体棒ab以初速度v0向右运动，匀强磁场磁感应强度为B，导体棒电阻为R，其余电阻不计，求安培力与导体棒ab运动位移的关系．

图2 证明用图

证明：

方法1：微积分证明

(6)

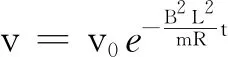
(7)

设t时刻安培力为

(8)

t时刻向前的位移

(9)

由式(8)、(9)可知

即

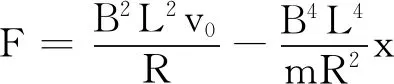
(10)

方法2:采用高中方法证明

设t时刻，位移为x，安培力为F

得

(11)

则安培力

(12)

以上两种证明结果是一致的，都说明该过程的变力安培力与位移成一次函数关系．如图3所示,在这种一次函数图像中，我们很容易用三角形或者梯形面积求出该过程中变力安培力做的功．也可以从表1中v-t图像和F-x图像对比理解．类比v-t图像我们得到了如式(14)瞬时速度与位移的对应关系，式(15)做功与位移的对应关系，式(16)做功与瞬时速度以及位移的对应关系．

图3 F-x成一次函数关系

表1 v-t图像与F-x图像对比

续表1

3 匀变速运动时

如图4所示，当光滑导体棒受到一个变力F从静止开始向右做加速度为a的匀加速运动．此时导体棒做匀变速运动，速度v=at与时间t之间本身就是线性关系，很明显这种情况下安培力能用“平均值法”这种快速解法思想解题．

图4 导体棒做匀加速运动

4 不存在线性关系的情况

5 平均值方法解题应用拓展

【例2】如图5所示，两根平行光滑金属导轨固定在水平桌面上，左边连接定值电阻R=2 Ω,导轨间距L=1 m．整个装置处在方向竖直向下的匀强磁场中，磁感应强度B=2 T.一质量m=1 kg、电阻r=1 Ω的金属棒放在导轨上，在外力F的作用下以恒定的功率P=12 W从静止开始运动，当运动距离x=3 m时金属棒达到最大速度，此时撤去外力，金属棒最终停下，设导轨足够长．求：在这个过程中，外力的冲量大小？

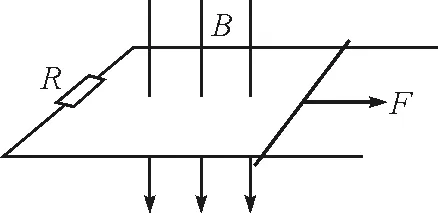
图5 例2题图

解法1：金属棒速度最大时，所受合外力为零，即

BiL=F

感应电流

根据电功率的计算公式

P=Fvm

联立解得

vm=3 m/s

设外力的冲量为I冲，作用时间为t，根据动量定理可得

I冲-BiLt=mvm-0

其中

所以有

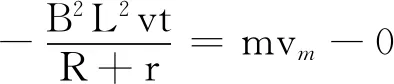
运动距离

x=vt=3 m

代入数据解得I冲=7 N·s

解法2：设F作用时间为t1，位移为x，撤去F后运动到停的时间为t2位移为d.

在撤去F阶段，由

(17)

得

(18)

对全程列式,由

(19)

【例3】如图6所示，电阻不计，间距为L的光滑平行金属导轨水平放置．导轨左端接有阻值为R的电阻．以导轨的左端为原点,沿导轨方向建立x轴,导轨处于竖直向下的磁感应强度大小为B的匀强磁场中．一根电阻也为R,质量为M的金属杆垂直于导轨置于x0处,不计金属杆与导轨间的接触电阻,现给金属杆沿x轴正方向的初速度为v0,金属杆刚好能运动到2x0处,在金属杆的运动过程中( )

图6 例3题图

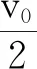
答案：A，B，D.

这里我们只讨论选项D.

解法1：对于选项D，由

令

(20)

当滑到1.5x0处时，设速度为v，时间为t1

-BiLt1=mv-mv0

(21)

解法2：

(22)

(23)

由式(23)有

(24)

式(24)代入式(22)得到方程

(25)

或v=-v0(舍去)

解法3：采用表1中式(14)直接代入求解

当位移为x0时速度为零

(26)

(27)

6 总结

综上所述可以得出，安培力“平均值法”在解题中有方便快捷的作用．对于其正确性，主要是基于:第一，当安培力随位移成一次线性函数关系成立时；第二，平均值本就是一种等效替代的思想．文中总结了3种情况下安培力“平均值法”可以应用：第一，导体棒只受到安培力做减速运动时；第二，有外力，但导体棒做匀变速运动时；第三，涉及用到安培力的冲量时．“平均值法”为学生在解决安培力的选择题提供了又快又准的解决方法．