基于随机场理论的纯黏土地基极限承载力分析
赵少飞,胡欣宇,邢明源, 鲍俊文
(华北科技学院 建筑工程学院,北京 东燕郊 065201)
0 引言
地基极限承载力确定,自1921年Prandtl给出了纯黏土地基的极限承载力以来,一直受到岩土学者们的关注。赵少飞等[1]利用显式有限差分程序FLAC2D对非均质地基承载力进行了数值分析,表明Skempton与Peck等建议的近似计算公式对条形基础下非均质地基的承载力产生了过高的估计[2,3]。在土的特性随机变化地基中,Li等[4]分析了不同埋深时地基承载力变化规律,表明土的参数空间变异性对地基承载力影响显著。
由于土是自然界产物,具有空间变异性。在天然条件下,土的物理和力学特性往往随空间位置而变化,相应的地基极限承载力具有随机性。为了更客观地确定地基承载力随土的参数随机变化特性,需要根据随机场理论,建立描述土参数空间变异性的地基随机场模型,分析相应的地基承载力特性。Vanmarcke[5]最先在岩土工程中引入随机场理论,较准确地反映土的实际特征。薛亚东等[6]利用随机场局部平均理论,采用强度折减法分析边坡的可靠性,结果表明若忽略土的随机特性,结果会有不同程度的偏差。Huang等[7]根据土的弹性模量空间变异性对隧道衬砌的变形进行可靠度分析。刘伯成等[8]利用随机场理论研究隧道开挖对建筑物的影响,为了保证建筑结构的安全性需要考虑土的空间变异性。王占盛等[9]利用改进的矩阵分解法对随机场进行反演,其结果表明改进的矩阵分解法对处理各向异性问题更加适用。孟建宇等基于随机场理论得出土体弹性模量空间变异性对沉降槽宽度、最大沉降值和最大沉降位置有重要影响。
自相关距离是反映土参数空间变异性的一个重要参数,其大小受土层的沉积年代、物质组成、地质环境等因素影响[11]。祁小辉等[12]分析了不排水抗剪强度的自相关距离对地基承载力的影响,计算结果表明承载力的均值和标准差随自相关距离增大而增大,随后学者比较了竖直和水平自相关距离对边坡工程的稳定性[13]和桩基承载力可靠度[14]的影响,表明竖直自相关距离的影响更加显著。刘雪莹等[15]基于Karhunen-Loève (K-L)展开法对随机场进行离散,得到随机场的离散误差随离散区域增加或自相关距离减小而增加。Griffiths和Vessia等分别给出自相关距离在0.5×2B(B:基础宽度)和0.3~0.5B范围内,存在最不利工况,但并没有指明自相关距离的具体值[16,17]。Zhu等[18]采用随机有限元法对不排水边坡的可靠性进行了研究。重点研究最坏情况下的空间相关长度,即边坡破坏概率达到最大的相关长度。结果表明,当平均安全系数较低或变异系数较高时,最不利情况现象最为明显。
本文在FLAC2D程序中通过编程建立土的黏聚力的随机场模型,分析黏聚力空间变异性对地基极限承载力影响,并与确定性数值解及解析解进行对比,进而探讨自相关距离所对应最不利工况。
1 黏聚力随机场地基模型
利用有限差分软件FLAC2D建立地基模型,取尺寸为20 m×10 m,条形基础宽度B为6m的二维地基模型的右半部分,即建立10m×10m(长×高)数值模型。在模型上方施加B为3 m的条形基础以更精确模拟地基模型,模型材料基本参数选自文献[15],见表1。

表1 模型中材料参数
在随机场地基模型中,随机土的参数仅考虑黏聚力一个随机变量,其他参数均为常量。将数值模型划分成n个单元格,遵循上述四个步骤生成n个服从正态分布的随机黏聚力值,并将生成的随机黏聚力赋值到FLAC2D软件所建立的地基模型中,边界条件及模型如图1所示。

图1 计算模型
在岩土随机场离散中,协方差矩阵分解法[19]容易实现,而且精度可以保证。这一方法被应用于隧道工程中[20-21],本文应用于地基黏聚力随机场离散。并且选择比较简单的Markov相关函数[22],生成n个黏聚力的随机参数。具体步骤如下:
(1) 地基模型单元剖分后,计算任意两个单元中心点距离τ,利用Markov自相关函数计算所有单元中心点之间的自相关函数ρ(τ):
(1)
式中,τ为随机场中任意两单元中心点的距离;θ为自相关距离。
(2) 根据上一步计算的单元间自相关函数值,构成协方差矩阵C,其维数为单元数量n的对称方阵。随后对其进行Cholesky分解,得到一个上三角矩阵和一个下三角矩阵:
C=LU=LLT
(2)
式中,U和L分别为上三角矩阵和下三角矩阵;LT矩阵L的转置。
(3) 产生n个服从标准正态分布的随机数,构成一个随机向量Y。进而生成一个n维的随机向量Z:
Z=LY
(3)
(4) 由随机向量Z和黏聚力的均值和方差,得到各单元的黏聚力为:

(4)
式中,σ和μ分别为服从正态分布的黏聚力的均方差和均值。
2 数值计算结果分析
2.1 自相关距离对地基承载力的影响
对于纯黏土地基上无埋深的条形基础,经典地基极限承载力解析解为cNc,其中承载力系数Nc为(2+π)。统计资料表明,土的黏聚力等参数自相关距离在0.1~3.0 m变化[23-24]。本文自相关距离θ取1.00 m、1.25 m、1.50 m、2.00 m和2.50 m共五种情况,对每一种自相关距离,分别进行数值计算确定地基极限承载力系数,分析自相关距离对地基极限承载力的影响。
随着自相关距离的变化,承载力系数见表2。在相同自相关距离条件下,承载力系数在一定范围内变化。承载力系数并不都随着自相关距离的增大而增大,当自相关距离θ取2.00 m时,反而更接近解析解,如图2所示。
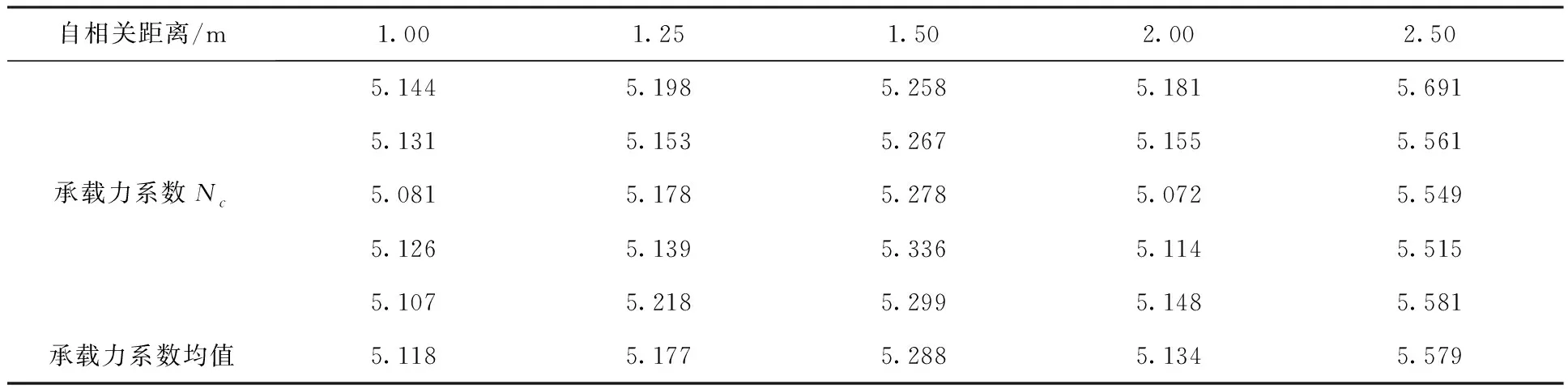
表2 自相关距离对地基承载力系数Nc影响
2.2 黏聚力随机场对地基承载力的影响
根据表1分别建立随机场地基模型和均质土地基模型并且施加同等宽度的条形基础并进行数值模拟,地基承载力系数随沉降量的增大而增大,最后达到极限状态,如图2所示。随机场地基模型的地基承载力系数分布在确定性数值解附近和解析解附近,这一结论与Griffiths等[25]的结论一致。
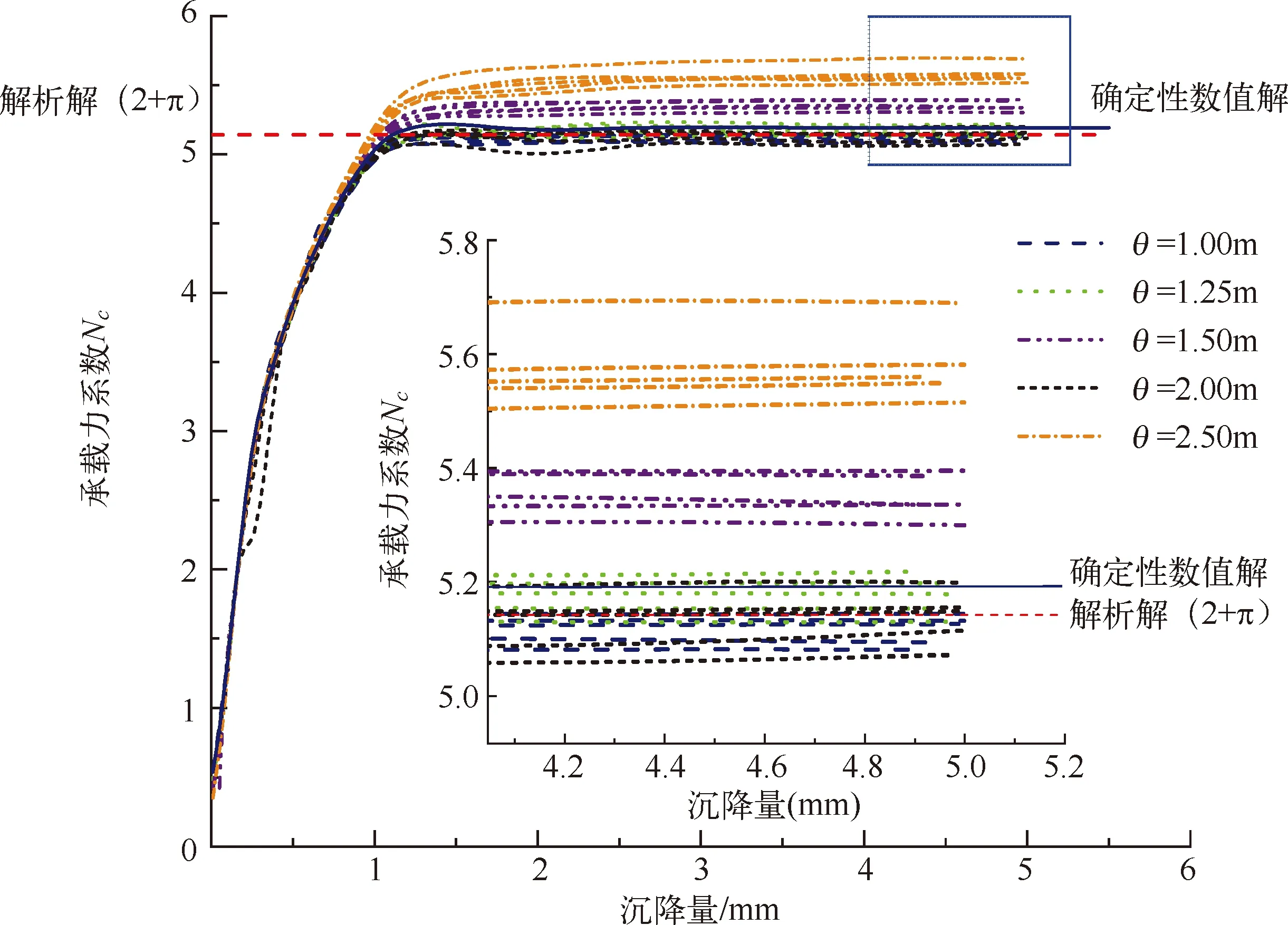
图2 不同土质条件下的地基承载力系数
由于每次模拟抽取的c值不同,即在同一自相关距离下,建立不同的随机场,得到地基承载力系数与自相关距离的关系,如图3。地基承载力系数随自相关距离的增大成非线性波动,且在同一自相关距离的条件下产生一定的波动范围。
从图3中看出,当自相关距离θ=2.00 m时,即自相关距离与基础宽度之比为0.33时,承载力系数均值低于其它自相关距离条件下的承载力系数均值,而且更加分散,同时在Vessia所提出的最不利工况范围内[26],因此可看作最不利工况所对应的自相关距离。

图3 不同自相关距离下的承载力系数
3 结论
(1) 将随机场地基与均质土地基和解析解进行比较,得出随机场条件下的地基承载力系数在确定性数值解和解析解附近波动。
(2) 在自相关距离取值范围内,地基承载力系数会随自相关距离的增大成非线性波动,且承载力系数有一定的分散范围。当自相关距离与基础宽度比为0.33时,纯黏土地基上条形基础作用下极限承载力存在最不利工况,但一般黏性土(c≠0,φ≠0)的最不利工况还需深入研究。
(3) 通过计算分析得知,在做相关承载力研究时需要引入随机场,使模拟条件更接近土的实际分布条件,以提高结果的准确性。

