改进蚁群算法的机器人路径规划研究
毛 嘉 琪
(湘潭大学信息工程学院 湖南 湘潭 411100)
0 引 言
移动机器人路径规划是当下研究热点,路径规划能力决定了移动机器人的智能水平。路径规划的主要任务是在具有静态或者动态障碍物的环境中,依据一定约束条件,寻找到一条没有碰撞的路径。其中路径规划算法显得极为重要。
现有常见路径规划算法有蚁群算法[1-4]、Dijkstra算法[5-8]、A*算法[6-8]、人工势场法[9-10]、遗传算法[11-12]等。在A*算法中,启发函数无法完全确定,可能存在多个最小值,极易陷入死循环。人工势场法在靠近障碍物时易产生震荡和陷入局部最优点,使机器人难以到达目标点。遗传算法涉及大量的个体计算,同时也容易陷入局部最优点,而蚁群算法因具有并行性、强鲁棒性[13]等优势在移动机器人路径规划问题的解决中得到广泛应用,传统蚁群算法主要是用于解决旅行商问题(Travelling Salesman Problem,TSP)。文献[1]改进了启发函数以及信息素挥发因子的更新规则,引入了以节点周围障碍物分布个数为变量的刺激函数,有效提高了算法的性能。文献[3]将当前节点和目标点的联系引入到启发函数中,提高了算法的收敛速度。文献[5]加入了进化选择概率,通过此概率来选择不同的概率转移公式,并且使用动态闭环调节来改进进化选择概率,提高了算法的抗干扰能力。文献[8]定义了一种新的引力函数,提高了算法的效率。文献[9]分析了蚁群优化中较为关键的参数,自适应调整算法参数,提高了算法的精度。
本文针对蚁群算法进行路径规划时存在收敛速度慢、易陷入局部最优以及初期信息素匮乏使得搜索初期比较盲目等问题,提出一种改进的蚁群算法。该算法首先使用改进的A*算法快速得到一条较优路径,来优化信息素初值。引入文献[1]的刺激函数到蚁群算法的启发函数中,提高路径避障能力。根据前后两次迭代的路径长度调整信息素更新,提高算法收敛速度。同时加入拐点参数来改变信息素挥发因子,使得算法路径搜索效率更高,更加稳定。在MATLAB软件中的仿真实验表明了该算法的有效性与可行性。
1 环境模型建立
三种常用的环境建模方法为网格法、几何法和拓扑图法[4]。栅格法地图较几何法和拓扑图法具有表达规范、易实现[1]等特点,本文采用栅格法对环境进行建模。
栅格法中采用1表示障碍物栅格,0表示自由栅格。栅格平台是一个二维环境,置于正交参考坐标系XOY中,计算每个网格的坐标。假设整个网格的标号都是整数,它们的长度等于坐标的单位长度[1],如式(1)所示。
(1)
式中:Nx是每一行的网格数;Ny是每一列的网格数;mod是余数运算;int是整数运算。
图1为一个网格映射环境模型,它每行有20个网格,每列有20个网格;黑色网格代表障碍,白色网格代表自由空间。

图1 栅格法环境模型
2 A*蚁群算法
A*蚁群算法的主要原理为借用改进A*算法先得到一条相对较优的路径并将此路径记为R,提高此路径上的信息素初值。在此基础上用改进蚁群算法继续搜索最优路径。这样既可以加快搜索速度,也可以减少蚁群算法搜索初期的盲目性。
2.1 基本A*算法分析及其改进
A*算法是一种启发式搜索算法,它把Dijkstra算法(靠近初始点的结点)和BFS(Breadth First Search)算法[8](靠近目标点的结点)的优点结合起来,在保证搜索效率的同时得到最优路径。估价函数为:
f(n)=g(n)+h(n)
(2)
式中:f(n)从初始状态经由状态n到目标状态的估计代价;g(n)在状态空间中从初始状态到状态n的实际代价;h(n)从状态n到目标状态的最佳路径的估计代价。
两种极端情况分别为:(1) 若h(n)为0,则只有g(n)起作用,此时A*演变成Dijkstra算法,这保证能找到最短路径;(2) 若h(n)远大于g(n),仅h(n)起作用,A*演变成BFS算法。
A*算法在搜索的过程中由于启发函数的帮助可以方向明确地前往目标点,但是当遇到障碍物的时候,也会在障碍物周围进行搜索。对此,在搜索过程中采用局部障碍物检测方法对最近障碍物进行预处理,在程序中,先将起始点向目标点做一条射线。一旦这条射线触碰到了障碍,则将障碍进行预处理。如果该射线没有碰到障碍,则说明前方路径上没有障碍物,那么就可以笔直朝着目标点前进。
首先记录下栅格图的障碍物的边界点,障碍物的边界点就是障碍物的起始点或者终止点(由起始点、方向向量、障碍物长度共同得到),如果是两障碍物相交,那么障碍物交点不会被当作是边界点,如图2所示。
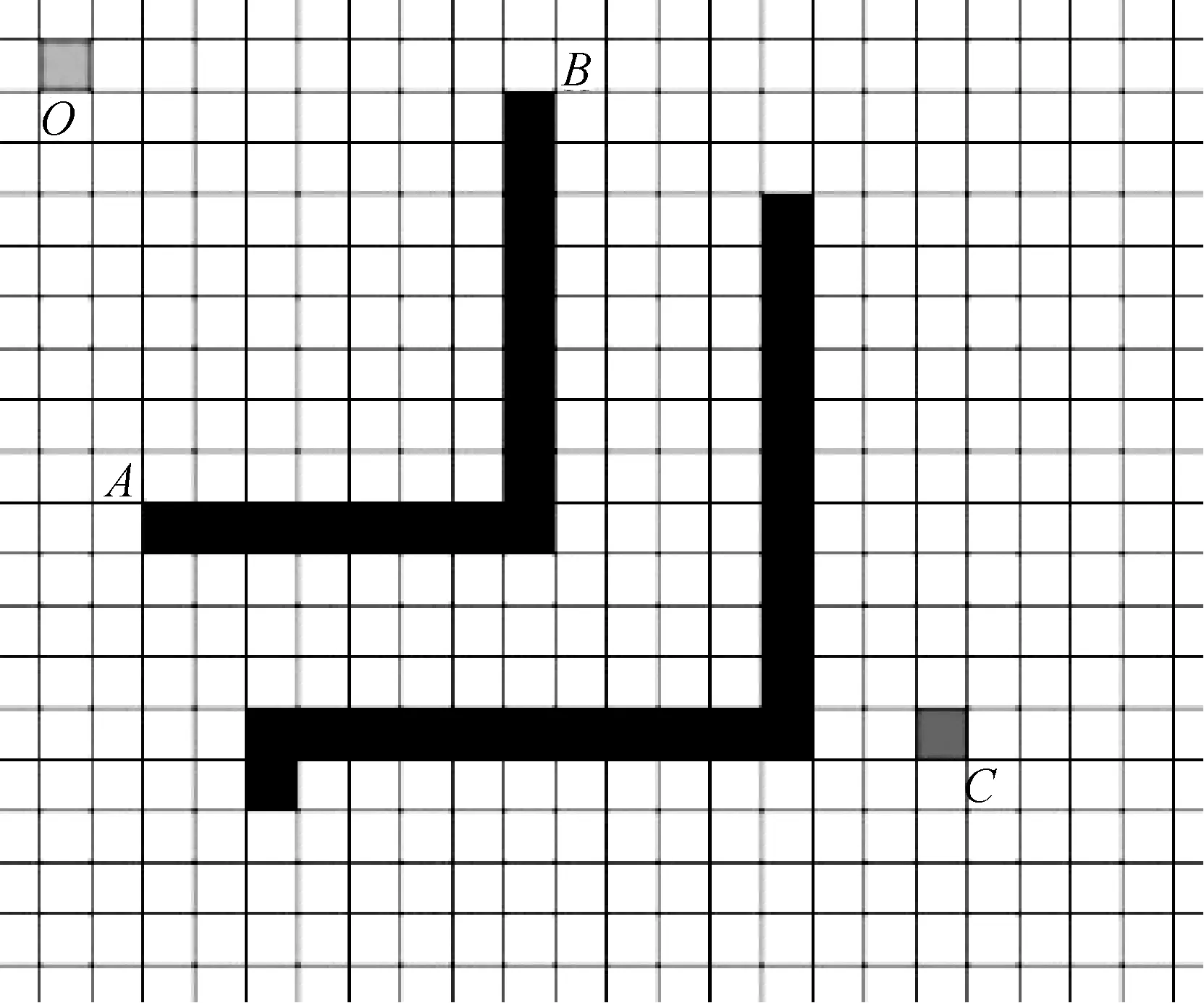
图2 智能车寻路时所遇障碍
图2中A、B为障碍物边界点,O为起始点,C为目标点)。然后需要计算OA+AC和OB+BC的绕行距离。假设此时选择从B点绕行,那么就将目标点临时改为B点,先规划出从O到B的路径,再将B点作为起始点,C点作为终点重复之前步骤。仿真对比结果如图3、图4所示。

图3 传统A*搜索范围
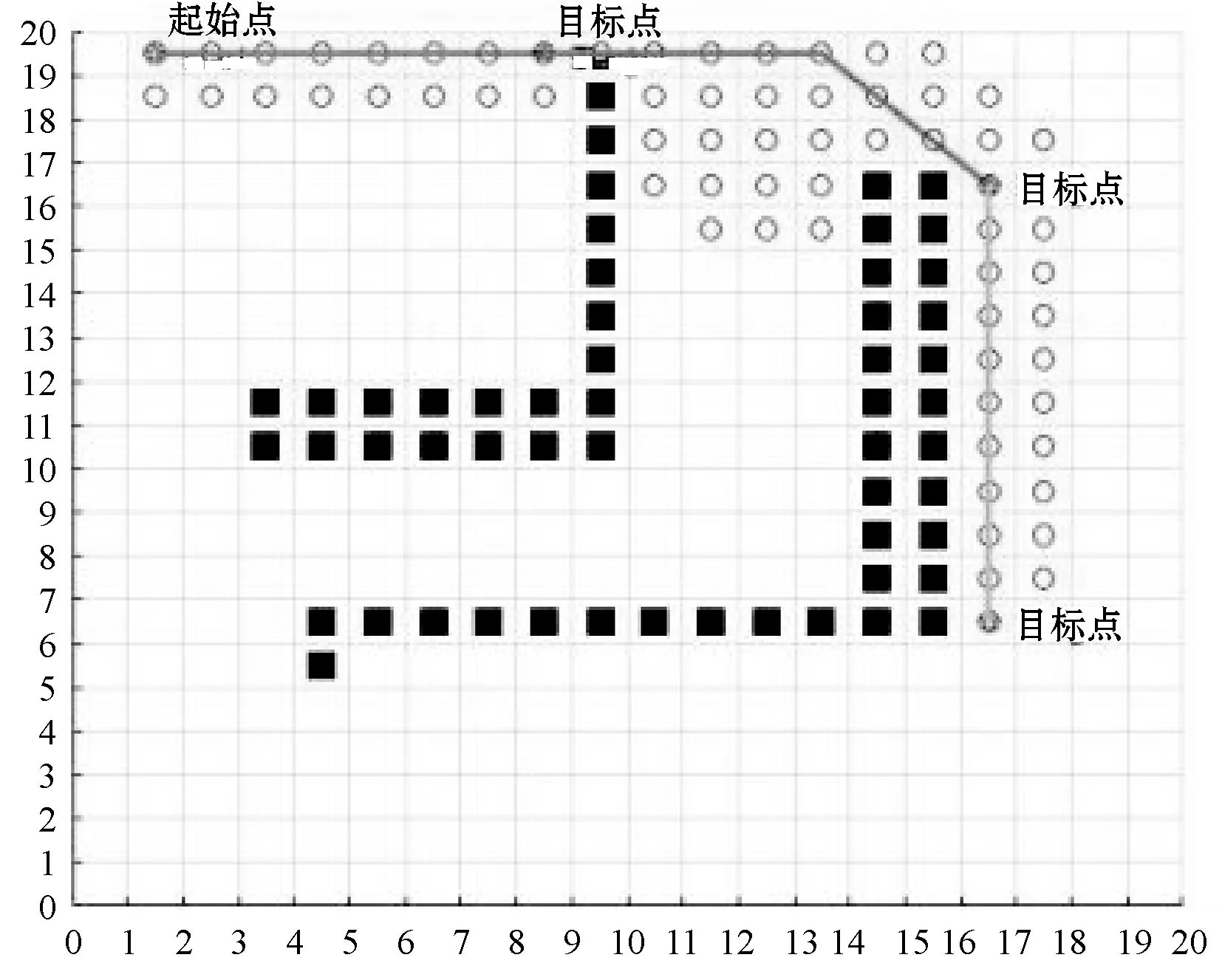
图4 改进A*搜索范围
2.2 基本蚁群算法
蚁群算法是一种模拟蚂蚁觅食行为的模拟优化算法,它是由意大利学者Dorigo等[12]于1991年首先提出,并首先使用在解决TSP(旅行商问题)上。之后,又系统研究了蚁群算法的基本原理和数学模型。
2.2.1概率选择
蚂蚁根据式(3)选择将要前进的节点。
(3)
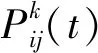
(4)
式中:dij为ij间的路径长度。
(5)
2.2.2信息素更新
每次所有蚂蚁完成一次寻迹后对全局的信息素进行一次更新,所有路径上的信息素水平将通过挥发旧的信息素和添加每只蚂蚁储存的信息素来更新[14]。信息素更新公式如下:
τij(t+n)=(1-ρ)·τij(t)+Δτij(t,t+n)
(6)
(7)
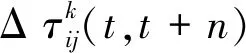
(8)
式中:Q是信息素增强系数,一般为1。
2.3 改进蚁群算法
2.3.1蚁群算法信息素初始化
将之前改进A*算法得到的路径记为R,并将路径R上的信息素初始化为:
τ(R)=NC
(9)
式中:N为大于零的常数,其余路径上的信息素仍然初始化为常数C。
2.3.2启发函数改进
为了让蚂蚁更容易地选择最佳的下一个网格,下一个网格必须是一个可访问的网格,并且有多个出口指向目标。这个概率取决于网格周围障碍物的数量。网格周围的障碍物越少,概率越大,网格就越有吸引力。这里引入文献[1]中的刺激概率SPij。
某网格j周围障碍物所有可能分布的情况个数可以计算为:
(10)
式中:Nobs为网格j周围的障碍物个数。
网格j的出口分布情况个数可以计算为:
(11)
SPij计算如下:
(12)
新的启发函数定义如下:
(13)
式中:djs为下一节点j与终点s之间的距离,增加了网格j与目标点的距离对启发函数的影响,同时增加了目标点对路径的吸引力。SPij增加了节点障碍物个数对节点选择的影响,节点j周围的障碍物越多,SPij越小,启发函数就越小,选择该节点的概率就越小。
2.3.3自适应信息素更新方式
为使蚂蚁能更快地搜索到最短路径,将信息素更新规则修改如下:
(14)
(15)
当上一路径Lk-1长度大于当前路径Lk,λ>1,则增加Lk的信息素增量。若上一路径Lk-1长度小于当前路径Lk,λ<1,则减少Lk的信息素增量。
2.3.4动态调整信息素挥发因子
信息素挥发因子ρ通常为一固定常数,可是若在全局搜索时ρ若为常数会降低搜索效率,现将ρ改进为:
(16)
式中:GDmT、GDmT-1分别为第T次迭代与第T-1次迭代中拐点参数平均值。机器人所寻路径中只有三种角,分别为锐角、直角、钝角,其相应值分别记为3、2、1,拐点参数值即所有角度值之和。
引入拐点参数来表征信息素的变化,当GDmT小于GDmT-1时,路径长度更优更平滑,此时减小ρ值,加快算法收敛速度,当GDmT大于GDmT-1时,增加ρ值,加强算法全局搜索能力。
2.4 改进算法的步骤
步骤1环境建模。
步骤2利用改进A*算法得到一条相对最优路径,并提高将此路径上的信息素初始值。
步骤3初始化蚁群算法参数,例如迭代次数、信息素因子和启发函数因子等。
步骤4将所有蚂蚁置于起点准备开始搜索。
步骤5根据转移概率选择下一节点。
步骤6在蚂蚁k完成搜索后,进行信息素的更新。
步骤7重复步骤5-步骤6。
步骤8将所有蚂蚁重置到起点,清空禁忌表。
步骤9判断是否达到迭代次数,达到设定值则结束程序,否则转步骤5。
算法流程如图5所示。
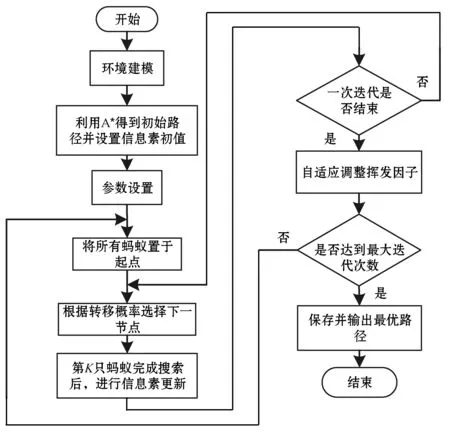
图5 算法流程
3 仿真实验
1) 将本文算法与文献[3]算法、文献[4]算法、传统算法进行比较。在文献[3]、文献[4]中的栅格环境(20×20)进行仿真实验。
本文参数设置如表1所示。
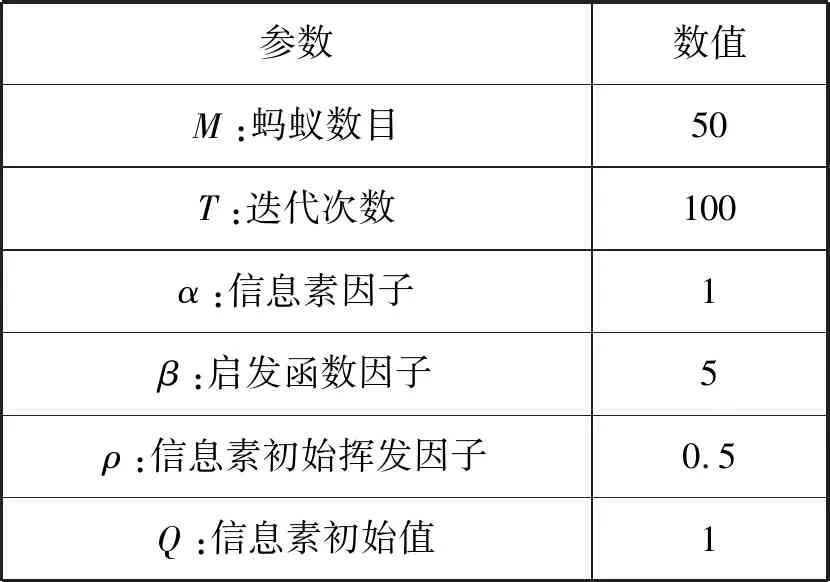
表1 参数设置
图6中虚线为文献[4]算法规划路径,实线为本文算法规划路径,两算法最短路径长度与迭代次数的关系如图7所示。

图6 文献[4]算法和本文算法的路径规划图
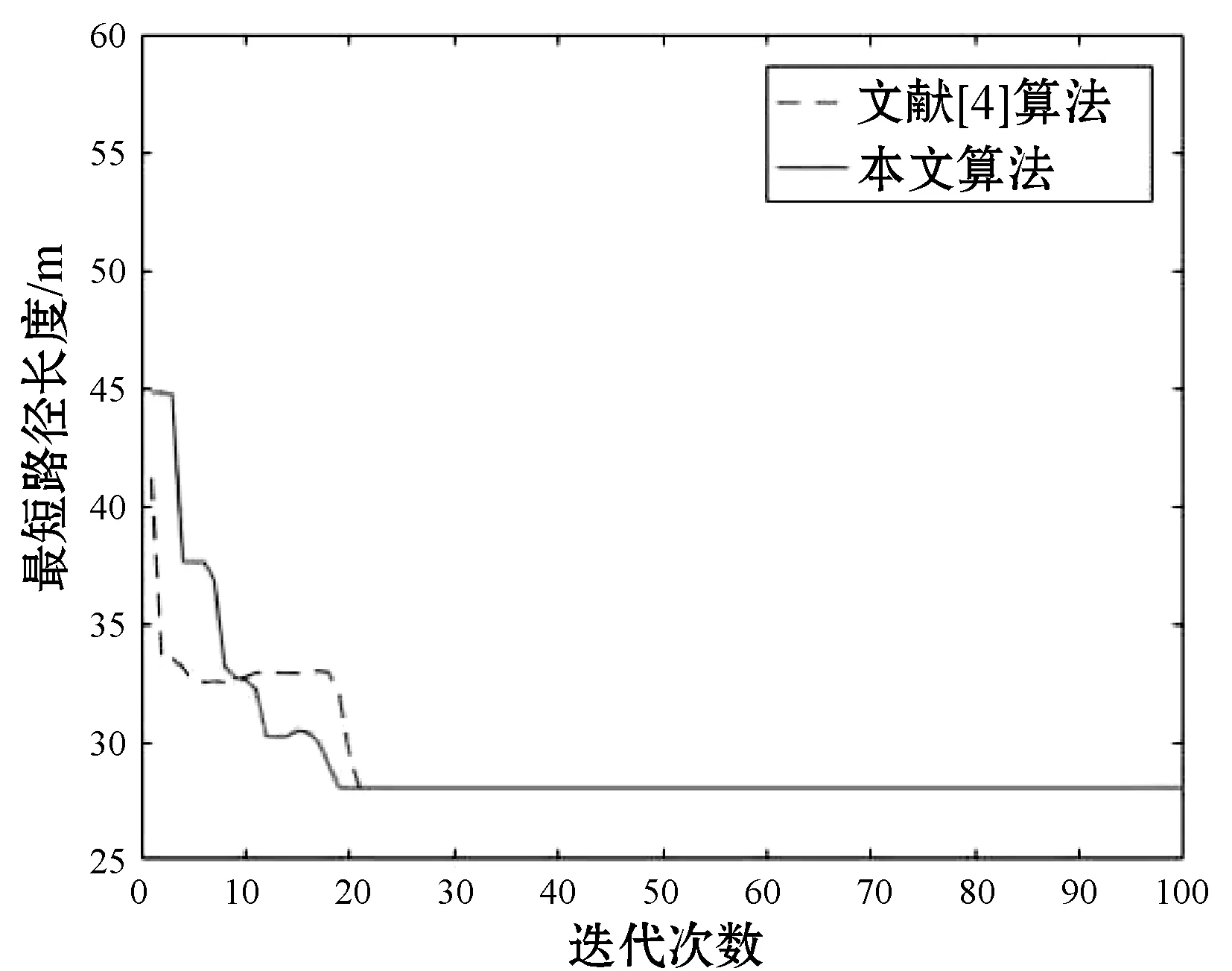
图7 文献[4]算法和本文算法的收敛曲线
由表2可知,在相同复杂度(20×20)和相同障碍物的情况下,本文算法与文献[4]算法路径长度相同,但是平均路径长度以及迭代次数均优于文献[4]算法,特别是由仿真10次的结果可以看出,本文算法比文献[4]算法有着更好的稳定性。

表2 文献[4]算法与本文算法对比
图8中虚线为文献[3]算法规划路径,实线为本文算法规划路径,两算法最短路径长度与迭代次数的关系如图9所示。
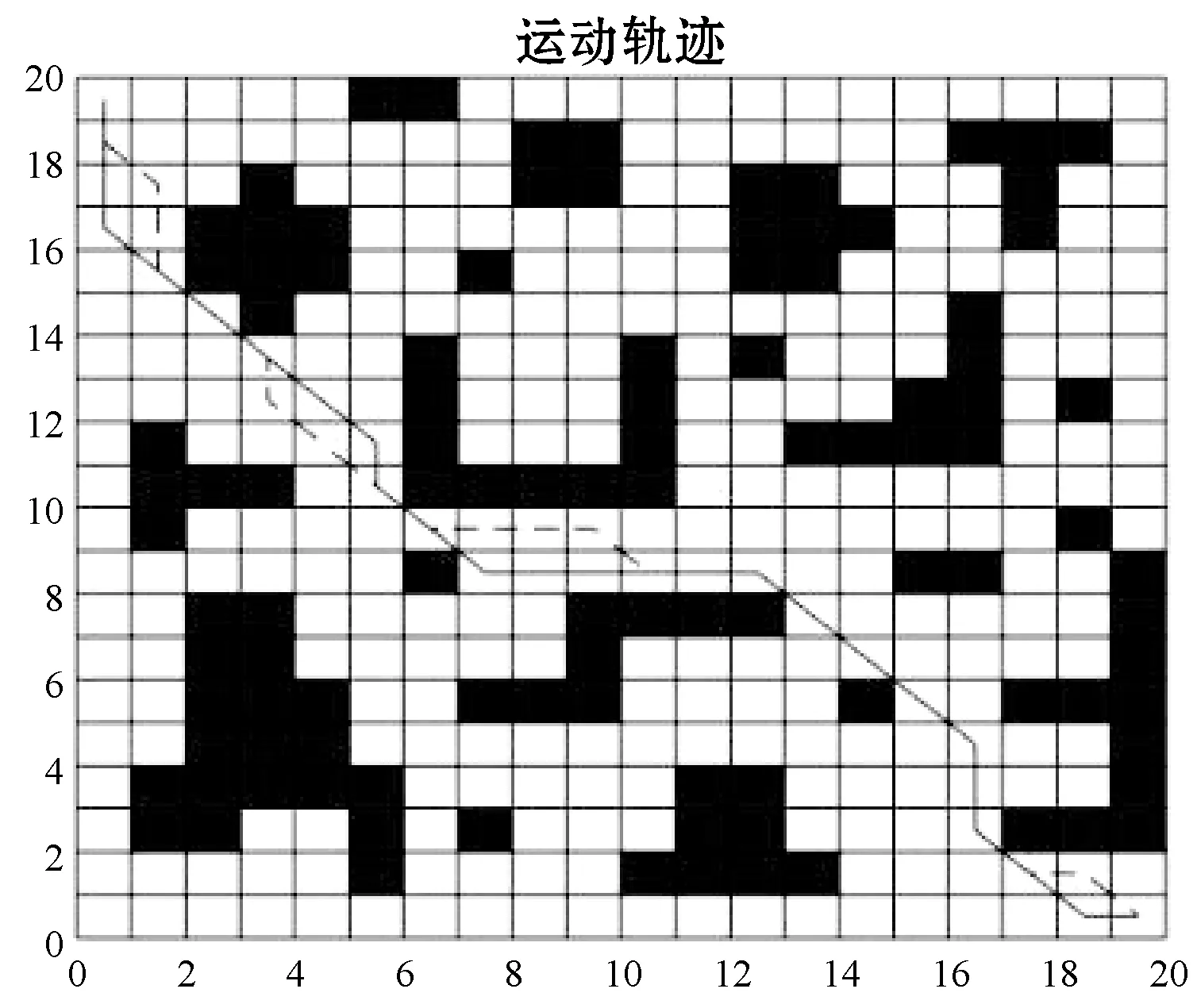
图8 文献[3]算法和本文算法的路径规划图
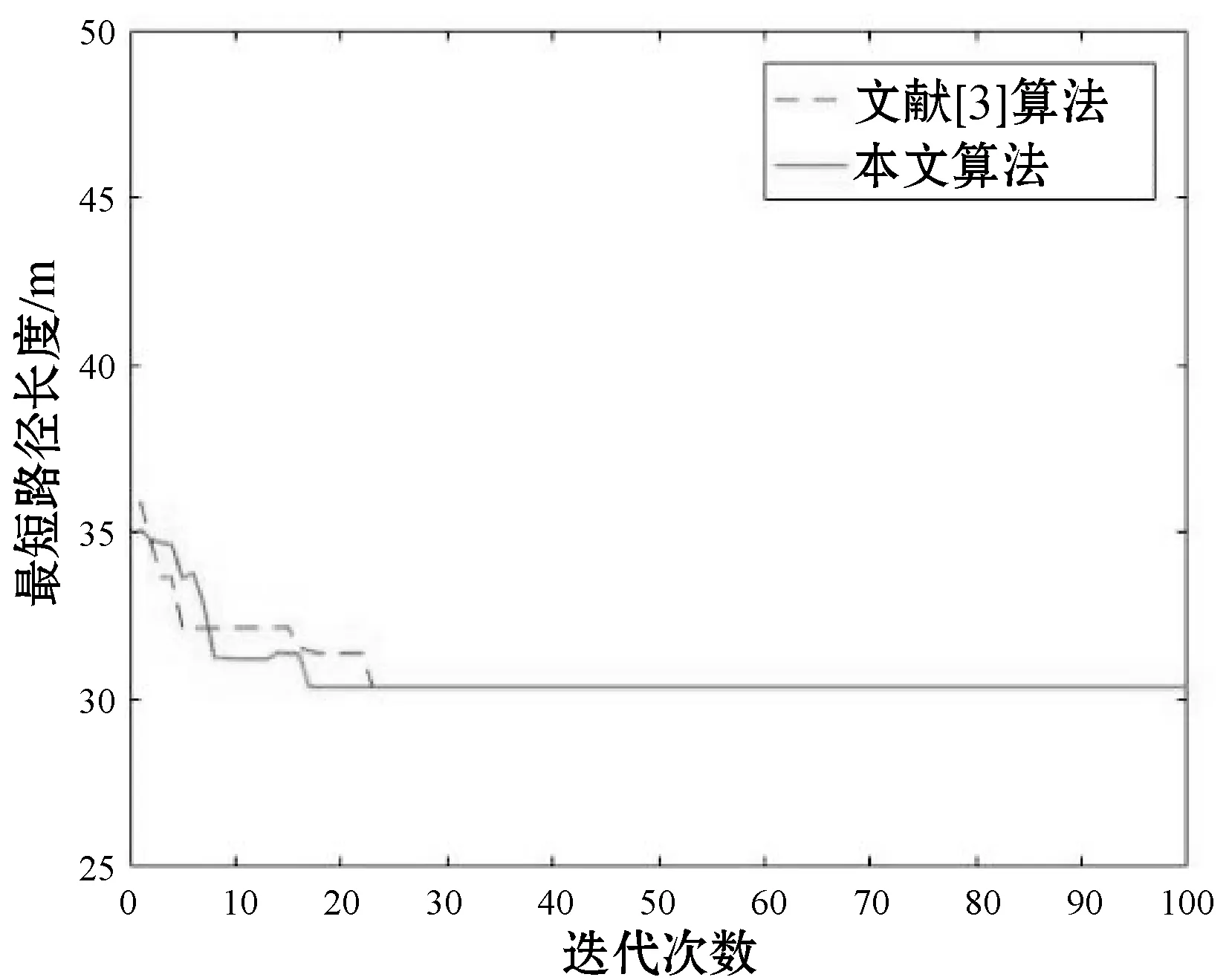
图9 文献[3]算法和本文算法的收敛曲线
由表3可知,在相同复杂度(20×20)和相同障碍物的情况下,本文算法与文献[3]算法相比最优路径长度相同,平均路径长度和迭代次数更优。
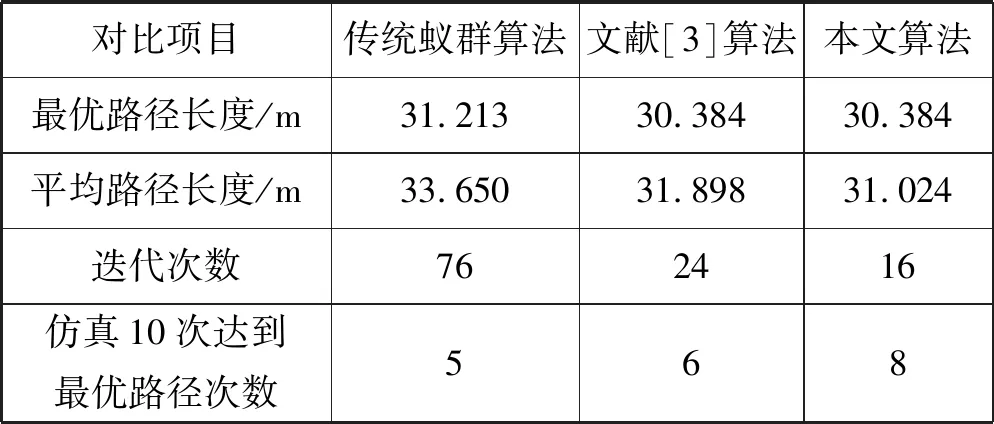
表3 文献[3]算法与本文算法对比
2) 在不同复杂程度的静态环境中进行仿真实验,实验参数设置如表1所示。
(1) 在10×10栅格环境中进行实验,路径规划结果如图10所示,路径长度为13.899 m,算法收敛曲线如图11所示。
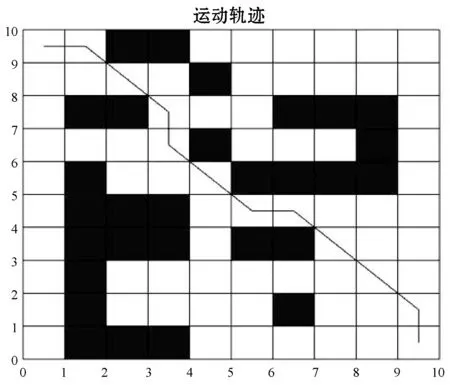
图10 10×10路径规划图
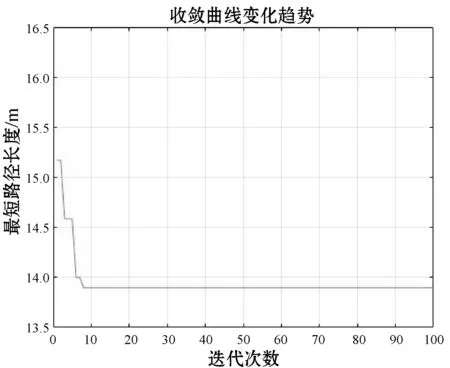
图11 10×10栅格环境中的收敛曲线
(2) 在30×30栅格环境中进行实验,路径规划结果如图12所示,路径长度为43.355 m,算法收敛曲线如图13所示。

图12 30×30路径规划图
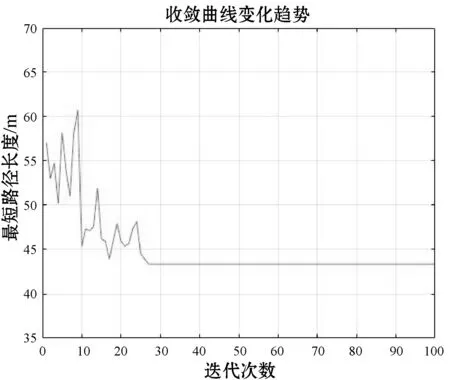
图13 30×30栅格环境中的收敛曲线
通过从简单到复杂的静态栅格环境中进行的多个仿真实验可以看出,本文算法不仅可以在简单的环境中规划出最优路径,在复杂的环境中也能规划出最优的路径,且迭代次数也较少,收敛速度快,适用于不同复杂度的环境。
4 结 语
针对传统蚁群算法在机器人路径规划中存在搜索时间较长、容易陷入局部最优、收敛速度慢等问题,本文对启发函数、信息素更新、信息素挥发因子进行了相应改进。仿真对比实验表明,本文算法不仅提高了搜索效率,加快了收敛速度,还可以在一定程度上提高解的稳定性。同时在不同复杂度下进行仿真,表明了本文算法的可行性与有效性。
本文主要针对静态障碍物情况下的全局路径规划,没有考虑存在动态障碍物时的情况,这也是本文的不足以及后续研究重点。

