稳定的K-多均值聚类算法

张倪妮，葛洪伟+

1.江苏省模式识别与计算智能工程实验室（江南大学），江苏无锡214122

2.江南大学物联网工程学院，江苏无锡214122

聚类分析是数据挖掘中的重要技术。它将一组没有标记的对象分组，使具有高度相似性的对象为一组。经过数十年的发展，研究人员提出了大量的聚类算法[1-5]。其中最经典的是K-均值聚类算法[1]。K-均值算法简单高效，其基于平方误差的划分方法在超球面簇中表现良好。但是它存在对初始点的选取敏感并且不擅长识别非凸模式簇的问题。

针对第一个问题，相应的改进算法有使初始聚类中心间距离尽可能大的K-means++[6]；基于蒙特卡洛取样进行初始化的方法AFKMC2[7]（assumption-freek-Markov chain Monte Carlo）；基于采样和密度峰值选择初始中心的方法SDPC[8]（sampled-clustering by fast search and find of density peaks）等。这些算法在一定程度上提高了K-均值算法聚类效果的稳定性，但是这些方法的聚类结果还是因为初始点的选取存在一定的波动。因此，K-均值类的算法如何选取初始中心仍是一个有意义的课题。

针对第二个问题，考虑到在很多实际应用中，每个类包含很多子类，不能用一个聚类原型来表示，出现了两类解决方法。第一类是非线性的聚类方法，例如基于核的聚类和谱聚类[9-13]；第二类是将每个类设置多原型的聚类方法，例如文献[14-19]。2019 年Nie 等人在ACM SIGKDD 上提出的指定k个聚类的多均值聚类算法（multiple-means clustering method with specifiedK，KMM）[20]属于第二类方法。该算法不同于其他同类方法，它将含多个次聚类中心的数据分配给特定的k类变成一个优化问题，交替更新数据对次聚类中心的划分和k个类的划分。这种方法解决了K-均值算法在非凸模式簇上的劣势，并且比同类方法用时更少，聚类效果更好。

然而KMM 算法作为K-均值算法的一种拓展，同样存在对初始聚类原型的选取敏感，聚类结果不稳定的问题。针对上述问题，本文提出了一种稳定的K-多均值聚类方法。该算法先计算出每个数据样本的最邻近样本，根据最邻近关系构造邻接矩阵，得到关于数据样本的图，将图中每个连通分支的均值点作为初始聚类原型。因为这种方法用到了每个数据样本的最邻近样本来寻找初始原型，所以将算法命名为FN-KMM（multiple-means clustering method with specifiedKby using first neighbor）。在人工数据集和真实数据集上的实验证明，与KMM 算法相比，FN-KMM的聚类结果非常稳定且效果更优。

1 KMM 算法及其缺陷分析

KMM 算法[20]的核心思想是将聚类原型的选取和数据对原型的划分变为一个优化问题，将数据和原型存在k个簇类作为限制条件加入到优化问题中，通过对优化问题的求解得到聚类结果。

令X=[x1,x2,…,xn]T∈Rn×d为数据样本矩阵，A=[a1,a2,…,am]T∈Rm×d为原型矩阵，第i个数据样本xi与第j个原型aj相连的概率为sij。通常情况下，xi与aj的距离越小，sij的值越大。因此KMM[20]将选取原型并将n个数据样本分配给它的相邻原型的问题写为如下形式：

根据文献[21]，KMM[20]将数据样本与原型存在k个簇类转换为限制条件添加到问题（1）中，得到问题（3）：

为了方便求解，KMM 算法[20]对限制条件适当放宽，并根据文献[22]中的定理得到了最终的优化问题（4）。

最后KMM[20]通过交替迭代的求解方法，完成对数据样本的聚类。

KMM 算法把多均值聚类问题转化为优化问题使得它的性能和速度比其他的多均值聚类算法更具优越性，但它存在K-均值类的算法普遍存在的对初始点选取敏感的问题，原型的选取极大影响了聚类的结果。

2 FN-KMM 算法

针对KMM 算法受初始原型的影响，导致聚类结果不稳定的问题，提出了FN-KMM 算法，这一章是对FN-KMM 算法的详细介绍。

2.1 初始次类原型的选取

通常情况下属于同一次类的数据样本间的距离要比属于不同次类的数据样本间的距离更小，且数据样本与它最邻近的数据样本属于同次聚类的概率最大。因此FN-KMM基于最邻近关系来选择初始原型。

定义2表示距离第i个数据样本最近的数据样本。

定义3Z∈Rn×n为基于数据样本的最邻近关系构造的邻接矩阵，Z中各元素的定义为：

计算所有样本与其他样本间的欧式距离。根据定义2 和定义3 得到邻接矩阵Z，构造图G=(V,E)，其中V是顶点（数据样本）集合，E是边的集合，Z(i,j)=1代表了第i个数据样本与第j个数据样本相连。记Cj为图G的一个连通分支，则可得到聚类原型aj=

KMM 算法根据用户输入的参数m或者默认，随机选取m个原型。用户很难估计出m的值，而默认的虽然有一定的合理性，反映了原型数目与聚类数和样本数的关系，但忽略了数据样本间的关系。FN-KMM 算法选取的初始原型其数目和位置不仅反映了样本的数量还反映了数据样本间的关系。原型数目不需要人为设定而是由基于最邻近关系构造的图G的连通分支数来决定，当两个样本中的一个样本为另一个的最近样本时两个样本相连，这样严苛的限制条件，可以保证构造的图有足够多的连通分支，避免了得到的原型数少于聚类数的情况。原型的位置是由图G中连通分支的点集决定，两个数据点距离越近属于同一类的概率就越大，每个点的最邻近点都属于同一个连通分支的点集，取连通分支点集的均值点为原型，原型的位置要比随机选取更合理。并且这种方法选取的初始原型不存在随机性，从而保证了聚类结果的稳定。

为了方便理解，用一个只有10个样本的二维数据集来解释选取初始原型的方法。数据集如图1 所示。

Fig.1 Sample dataset图1 数据集样例

计算样本数据间的欧式距离，得到每个数据样本最邻近的样本，构造如图2（a）所示的邻接矩阵Z，根据该矩阵可以构造图如图2（b）所示。

Fig.2 Demo of looking for initial prototypes图2 寻找初始原型的演示

2.2 求解优化问题

FN-KMM 在得到了初始原型后，可用交替迭代的方法来对优化问题（4）进行求解[20]。下面是求解过程的具体描述。

2.2.1 固定A 并更新S、F

当A固定后，问题（4）转化为问题（6）如下：

问题（6）同样也可以用交替更新的方法来解决。当S固定后，将F和D改写成如下形式：

其中，U∈Rn×k，V∈Rm×k，DU∈Rn×n，DV∈Rm×m。问题（6）可以被转化为问题（7）如下：

问题（7）可以通过文献[23]中提出的定理1 来解决。

定理1设A∈Rn×m，X∈Rn×k，Y∈Rm×k，且有问题如下：

F更新后，固定F。问题（6）转变为问题（9）：

根据如下关系（10）：

因为问题（11）在不同的i之间是独立的，所以可以分别对每个i解决问题（12）如下：

2.2.2 固定S、F 并更新A

当S、F固定以后，A可以根据式（15）来进行更新。

当A的赋值或数据样本的次类划分不再变化时，算法收敛，停止迭代更新。

2.3 FN-KMM 算法步骤

FN-KMM 算法流程简单描述如下：

步骤1通过计算数据样本之间的距离来求每个样本的最邻近样本。

步骤2根据式（5）求邻接矩阵Z，构造图G，得到图G中的m个连通分支。

步骤3计算m个连通分支的数据样本均值，求得原型矩阵A∈Rm×d。

步骤4对每一个i，用文献[12]的方法求解问题（16），计算S的第i行。

步骤8对于每一个j，根据式（15）更新A的第j行。

步骤9重复步骤4～步骤8 直到收敛。

2.4 算法复杂度分析

假设聚类对象有n个样本，d个维数。在寻找初始原型这一阶段，时间复杂度主要是由计算样本间的距离和使用kd-树来获得最邻近样本产生。因此，FN-KMM 算法在寻找初始原型阶段的时间复杂度为O(nlogn+nd)。

更新F所需要的时间复杂度主要是由计算S～ 的奇异值分解产生，为O(m3+m2n)。更新S所需时间复杂度为O(nmk+nmlogm)。设交替更新S、F的迭代次数为t1。通常情况下，m3与logm的值较小因此迭代更新S、F的时间复杂度为O((nmk+m2n)t1)。根据式（16）可知，更新A所需时间复杂度为O(nmd)。

综上，假设A参与了t2次迭代，那么FN-KMM算法总的时间复杂度为O(n((mk+m2)t1+md)t2+nlogn+nd)。

由文献[20]可知KMM 算法的时间复杂度为O(n((md+mc+m2)t1+md)t2)。FN-KMM 虽然在选取初始原型的过程中比KMM 耗费了更多时间，但是与KMM 一样算法复杂度都是关于n的线性缩放，属于一个量级。

2.5 算法收敛性分析

FN-KMM 算法的目标函数可写为式（17）的形式。

其中，S∈Ω可以看作是数据和原型可以被分为k个簇类的限制条件。S可看作EM（expectation-maximization algorithm）算法中的隐藏变量，A可看作其他参数。求解目标函数的过程可看作EM 算法中交替更新隐藏变量与其他参数直至收敛的过程。EM算法的收敛性在文献[24]中已经给出了证明。综上FN-KMM 算法是可收敛的。

3 实验与分析

这一章展示了FN-KMM 算法在人工数据集和真实数据集上的表现，同时将FN-KMM 与KMM[20]、Kmeans[25]、KKmeans（Mercer kernelk-means）[26]、MEAP（multi-exemplar affinity propagation）[18]、K-MEAP（multiple exemplars affinity propagation with specifiedkclusters）[19]这些优秀算法进行对比。

3.1 聚类结果评价

实验中使用准确率（Accuracy）、标准互信息（normalized mutual information，NMI）和纯度（Purity）三个聚类评价指标来对算法进行对比。设C为真实聚类结果，W为算法得到的结果。准确率的定义如下：

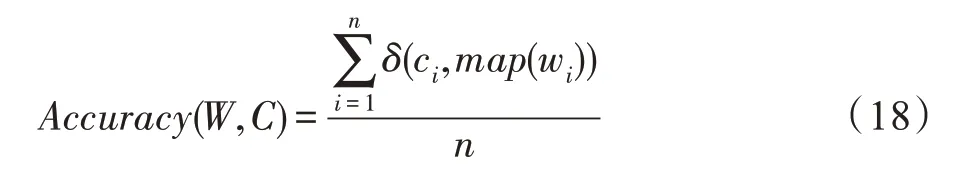
其中，map为最佳映射函数，可以将算法得到的标签与真实聚类标签变为一一映射的关系。δ是指示函数，定义如下：

标准互信息的定义如下：

其中，I表示互信息，H表示信息熵。

纯度的定义如下：

评价指标Accuracy、NMI、Purity 的值越大，聚类性能越好，评价指标的取值范围是[0,1]。

3.2 实验结果与分析

为了验证FN-KMM 算法的性能，分别在人工数据集和真实数据集上进行实验。

3.2.1 人工数据集的实验结果分析

将FN-KMM 算法与KMM 算法分别在表1 中的4个人工数据集上进行实验。

Table 1 4 artificial data sets表1 4 个人工数据集信息

表1 中，D1 由两个团状簇和一个流形簇构成；Aggregation 由6 个团状簇构成，其中个别团状簇相互连接；Zelink1 由两个团状簇和一个流行簇构成；Zelink3 由一个团状簇和两个环状簇构成。

图3 和图4 分别为KMM 算法和FN-KMM 在4 个人工数据集上的表现。

Fig.3 Clustering results on artificial data sets by KMM图3 KMM 在人工数据集的聚类结果

图3 和图4 中红点表示的是原型，不同类别的样本点用不同颜色来区分。KMM 随机选取原型的方式导致了聚类结果波动很大。当原型选取不佳时，如图3 所示算法不能得到正确的聚类结果。而FNKMM 通过数据样本的最邻近关系寻找原型，不仅结果稳定，没有任何波动，并且如图4 所示可以得到正确的聚类结果。

3.2.2 真实数据集的实验结果分析

为了进一步验证FN-KMM 算法性能，分别将K-means[25]、KKmeans[26]、MEAP[18]、K-MEAP[19]、KMM[20]和FN-KMM 在表2 中的真实数据集上进行展示。

Fig.4 Clustering results on artificial data sets by FN-KMM图4 FN-KMM 在人工数据集的聚类结果

Table 2 6 real data sets表2 6 个真实数据集信息

表2的数据集中BinAlpha与Palm为图像数据集，256个属性值是图片的像素值，除了Ecoil[27]与Abalone[27]有文本属性需转换为离散值外，其他数据集的属性均为连续值。为了取得更好的聚类效果，数据集的属性值在转为数值型数据后进行了归一化处理。

表3 中K-means、KKmeans、MEAP、K-MEAP、KMM 在6 个数据集上的运行结果全部取自文献[20]。K-均值类的算法会因为原型的选择而产生波动，对于这些有波动的算法，表中的数据是它们运行100 次后结果的平均值和标准平方差。MEAP、K-MEAP 在数据集Htru2 上的运行结果由于时间过长因此没有展示，表中标粗的数据为各个算法在该数据集上表现最好的结果。

针对K-means 算法对非凸簇或大小形状差异大的簇聚类时效果不佳的问题，KKmeans 将输入空间的数据样本映射到高维特征空间中，并选取合适的核函数代替非线性映射的内积，在特征空间进行聚类分析。从实验结果看，这种方法在个别数据集上有微小的改善，远不如通过设置多个次类来提高聚类效果的方法。而在K-means基础上设置多个次类的KMM 与FN-KMM 算法比在近邻算法基础上设置多个次类的MEAP 与K-MEAP 算法聚类效果更优。尤其是FN-KMM 算法在大部分数据集上取得了最优的结果，作为对KMM 算法的一种改进算法，在BinAlpha上的准确率甚至比KMM 算法提高了10 个百分点左右。值得一提的是KMM 算法因为随机选取原型所以算法效果波动很大，一些数据集上标准方差能达到7%。而FN-KMM 通过最邻近关系来选取的初始原型是确定的，因此最后得到的聚类结果非常稳定，不存在任何的波动。此外在人工数据集和真实数据集上的实验表明，由于数据集的不同FN-KMM 的收敛速度略有差异，但所有实验经过15 次以内的迭代都能取得令人满意的聚类结果。

Table 3 Performance of different algorithms on real data sets表3 不同算法在真实数据集上的表现%

4 结束语

针对KMM 算法随机选取初始原型，并且聚类结果不稳定的问题，提出了FN-KMM 算法，它可以自动确定原型的数量和位置，取得稳定且更优的结果。

FN-KMM 算法在一定程度上提高了KMM 算法的性能，避免了结果的波动，但是也牺牲了一定的运算时间。在一般数据集上FN-KMM 与KMM 在运算时间上的差异并不明显，在样本数较大的数据集上这种差异会更明显。如何提高算法的计算效率并减少算法的运算时间将是后面的研究重点。