传感网中带有可控阈值的优化协同覆盖算法

孙泽宇，李传锋，邢萧飞，来纯晓

1.洛阳理工学院计算机与信息工程学院，河南洛阳471023

2.河南科技学院信息工程学院，河南新乡453003

3.广州大学计算机科学与网络工程学院，广州510006

无线传感器网络实现了信息世界与物理世界有机统一，改变了人类世界对物理世界交互方式，其广泛地应用在国防军事、安全生产、医疗卫生、环境监测、目标跟踪和智能交通等多种工程领域[1-3]。无线传感器网络物理特点主要表现在：在监测区域内随机部署大量传感器节点，以监测移动目标节点或某发射源，传感器节点通过自组织方式形成信息交互和数据实时采集的大型网络[4-6]。监测区域内，任意传感器节点都具有一定的存储能力、通信能力、计算能力和感知能力，但各种能力均较弱[7]。其工作的动力来源于自身的电池，一旦电能耗尽将无法补充[8-10]。因此，覆盖效果的优劣直接影响到无线传感器网络体系结构、网络协议、目标定位与跟踪、能量高效和网络通信。为此，构建一个可靠、实时、高效的无线传感器网络系统是一项艰巨而有挑战性的工作。

随着国内外学者对群体智能方面研究的不断深入，现以智能分簇结构下的覆盖算法进行分析。文献[9]以节点能量作为研究背景，以单位时间作为轮流基数，让高能量节点作为簇首节点，同时利用贪婪算法计算了相邻节点之间的最短路径。文献[10]利用双链表写入数据传输所行走过的路径；当某一个路径出现故障时，另一个链表中获取上一级别的节点路径信息重新写入该链表，然后再次更新双链表，以达到路径双备份目的。文献[11]利用图论树型结构构建一棵无向生成树，而后通过簇内中心节点广播路由，优先搜索得到一棵最小路由生成树，再次利用蚁群算法遍历最小生成树，最终得到簇内最优路由。文献[12]利用退火算法构建路由最小生成树，以簇内能量最高节点作为簇首节点，以能量次高节点作为副簇首节点。通过退火算法计算得到最小延时路径，并将数据发送至基站；在数据融合阶段，则是利用簇内成员节点的位置信息与相邻节点的位置信息构建上一层的能量均衡路由树，以达到全网能量平衡的目的。文献[13]利用非线性优化原理，给出了传感器节点与目标节点的最大连通计算方法；然后利用排序算法按照能量的高低进行排序并将节点存储在有限链表中。在对目标节点覆盖过程中，从链表中按照节点能量从高至低的顺序进行选举，最终达到整个网络能量均衡的目的。文献[14]以数据融合时间作为研究对象，给出了一个基于局部数据融合信息的分布式路由算法，该算法可以为任意一棵生成树建立最优传输路径，同时也为任意一个传感器节点指定了数据的时间间隙，优化的网络资源。文献[15]利用退火算法通过传感器节点剩余能量和数据的相似性建立节点的分簇。对于簇内成员所采集的数据信息则通过回归模型获取预测数据，以此决定数据的传输路径。文献[16]给出了一种基于数据行为的分布式算法。该算法把静态与动态成簇算法相融合对簇内成员进行动态划分，在本周期内所在簇内成员节点均保持静态；在若干个周期后，根据传感器节点能量与欧氏距离关系采用动态成簇方法对所有节点再次划分，最终达到能量均衡目的。文献[17]利用传感器节点感知能力的连续性和传感器节点连通性等特性，提出了多目标连续跟踪算法。该算法也是通过簇间通信完成了对移动目标的跟踪过程，簇首节点将簇内成员所采集的数据信息进行有效融合，最终由簇首节点转发给基站。文献[18]对原始簇首选举阈值函数进行改良，结合间距因素、节点剩余能量和节点位置因素提出新的簇首选举函数，有效延长网络生命周期，但簇首的选取依赖随机概率和阈值函数，因此无法保证簇首选取结果的最优性。

覆盖问题首先要建立研究的覆盖模型，提高覆盖精度及准确性，同时要抑制传感器节点能量的快速消耗，以达到延长网络生存周期目的；其次，对于监测区域而言，为了抑制节点的能量的消耗，覆盖过程中并不需要对整个监测区域覆盖，而采用对关注目标节点的有效覆盖。再次，为了更好地对关注目标节点进行有效覆盖，这就要求节点之间建立协同工作，将网络中的地理位置相邻的节点划分为相连的区域，构成分簇结构。为了进一步研究覆盖问题，本文以感知智能计算和可控阈值作为研究背景，提出了优化协同覆盖算法。本文的主要贡献体现在以下三点：

（1）引入覆盖模型并对该模型进行有效分析，给出相关定义及模型分析过程。

（2）通过可控参数和遗传算法中变异参数等特性对事件域节点成簇进行优化，提高覆盖的精准度，优化了网络资源，提升对全局目标节点的搜索能力。

（3）通过仿真实验验证本文OCC-CT（novel optimization cooperative coverage algorithm with controllable threshold-parameters）算法的稳定性和有效性。

1 覆盖模型建立与分析

1.1 假设与基本定义

本文在研究覆盖问题时，需要将现实的物理问题转换成抽象的数学问题。为了便于研究问题的方便性，故作出如下假设：

（1）在监测区域内，忽略传感器节点边界效应，其感知半径远小于监测区域边界长度。

（2）网络中的每个传感器节点都可以通过某定位算法获取自身位置信息，如RSSI（received signal strength indication）、TDOA（time difference of arrival）。

（3）每个传感器节点感知能力不受外界物理环境影响，具有唯一标识[19-20]。

（4）网络初始时刻，所有节点呈现同构形态且始终保持圆盘形，感知半径均相同，所有传感器节点的通信半径均相同[21]。

（5）每个传感器节点工作时均与时间同步，网关节点不可移动。

定义1（覆盖率）在无线传感器网络内的被所有传感器节点监控或跟踪的可靠性，也称为覆盖程度或覆盖度。覆盖率是所有传感器节点覆盖区域的大小与整个目标区域大小的比值[3]。

其中，C为覆盖率；S(Ai)为第i个节点的覆盖区域的大小；N为传感器节点的数量；S(A)为监测区域面积。

定义2（覆盖效率）在监测区域内，所有传感器节点的覆盖面积并集与所有传感器节点覆盖的面积之和的比值[10]。

覆盖效率反映了传感器节点覆盖的冗余程度，覆盖效率与节点冗余程度成反比，即：高覆盖率，低冗余度；反之亦然。覆盖效率也是每个节点的平均覆盖率。

定义3（覆盖重数）给定一个平面监测区域，如果其中的任意一个物理位置都至少落在k个传感器节点的感知范围之内，则称无线传感器网络k-度覆盖[14]。

其中，KA为S(A)区域的覆盖重数；ki为第i个节点感知范围。在某些应用环境下，并非对全网进行完全覆盖，只要完成对所关注目标节点覆盖即可，这称为部分覆盖或有效覆盖。

定义4（覆盖均匀性）一般用节点间距离标准差加以表示，即：

其中，U表示为在监测区域内，节点覆盖均匀特性参数，n为传感器节点总数量；Ki为第i个节点的邻居节点个数；di,j为任意两个节点之间欧拉距离；Mi为第i个节点与其相邻节点距离的平均值。

定义5（覆盖时间）目标被完全覆盖或者跟踪时，所有工作节点从启动到就绪所需要的时间[16]。

定义6（支配集）在图G=(V,E)中，若找到一个V的一个子集S⊆V，S≠∅，对于∀si⊆V-S，S都至少与V-S中的一个节点相邻，则称S是图G的支配集（dominating set，DS）。DS 中的节点称为支配集节点，不在该集中的节点称为被支配节点，即：图中的每个节点都属于子集或至少是子集中一个节点的邻居节点[18]。

为了进一步研究网络覆盖问题，本文将传感器节点划分成若干个簇。分簇的主要目的在于：实现全网能量的均衡，达到簇内节点能量的平衡；提高网络覆盖效率；抑制由延时带来的能量快速消耗；增加连通性并减少延时；实现最小化簇数量，从而延长网络生存周期[22-24]。分簇的主要任务在于：对移动目标节点进行实时连续覆盖，并按照分簇要求将若干传感器节点划分成多个可以相互通信，覆盖所有传感器节点的多个簇，当网络拓扑结构发生变化时，可以随时更新簇结构以便更好修护和管理簇；共组织形式主要体现在将地理位置不同的若干个相邻传感器节点通过感知能力划分为大小不一的簇，从而便于完全对移动目标节点的有效覆盖。分簇结构下的移动目标节点的覆盖如图1 所示。

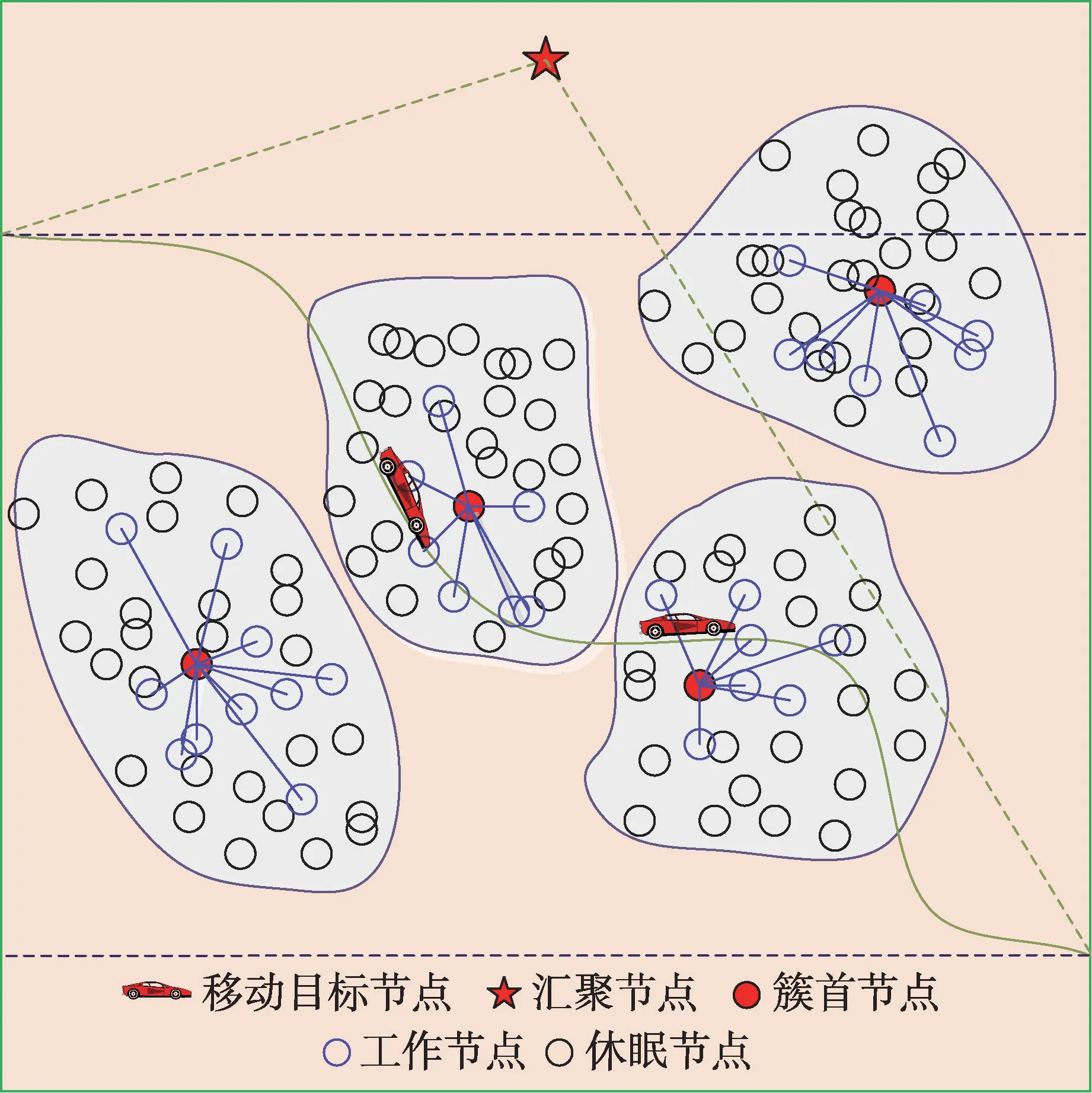
Fig.1 Network coverage model of mobile target nodes under cluster structure图1 分簇结构下的移动目标节点的网络覆盖模型

图1 给出了分簇结构下的移动目标节点的网络覆盖模型。从图1 中可以看出，本文将传感器节点划分成四个簇，当移动目标节点处于某个簇当中时，就可以完成对移动目标节点的有效覆盖；当移动目标远离该簇时，由该簇的簇首节点向相邻簇首节点发送消息，并唤醒相邻的簇首节点继续对移动目标节点进行有效覆盖。在研究覆盖过程中，不需求对整个监测区域进行有效覆盖，而只对移动目标节点进行有效覆盖，其目的是抑制节点能量的消耗，延长网络生存周期。

1.2 覆盖模型分析

在上述分析的基础上，为了进一步提高覆盖效率，延长网络生存周期，优化簇内结构，本文引入了智能算法中的遗传算法对覆盖率和簇结构进行优化，以达到覆盖最优效果。

对于给定的传感器节点集合S={s1,s2,…,sN}，个体si∈S的适应值为f(sj)，其选择概率为：

式（6）决定了下一周期传感器节点集合中个体的概率分布。其中，上一周期中传感器节点的生存期望数目为：

在节点集合中，传感器节点自身差异性较大，如能量、感知距离等因素，使得最优和最差节点选 择概率出现明显不同，因此，在下一周期内，最优节点选择概率将会较高，而最差节点被选择的概率将会较低。交叉操作是智能进化算法中GA（genetic algorithm）算法具备的原始性的独有的特征。在动态分簇过程中，为了增加簇与簇之间的重组，本文采用了交叉操作。对于选定的多个簇，随机选择多个交叉点，构成新的交叉集合。

将L位节点重新划分到新簇的相关位置的集合为：

算子形式定义为：

在采用不同的交叉算子对GA 定性计算时影响较大，在不同的簇内随机选取两个不同节点si、sj，可按下列进行交叉操作。

再对WSNs（wireless sensor networks）中传感器节点进行重新划分成簇时，当时间为t1=T时，某簇中的节点重新划分到另一簇时，对于本簇而言，其链表结构发生了变化，就可以认为该节点发生了变异。在遗传算法中，变异算子是通过按变异概率pm随机反转某个传感器节点来实现的，公式如下：

适应值函数是评价重新组建簇内成员覆盖质量的可行解集，是评价所需要的关于节点适应值函数的计算次数。显然，该值越小说明相应的GA 的搜索效率越高。适应值函数分为在线搜索和离线搜索两种形式。

在线性能反映了节点集合平均适应值经平滑处理后的变化情况，描述了节点集合的整体性和进化能力。

其中，f(a*,t)=max{f(a1,t),f(a2,t),…,f(an,t)}，即当前节点集合中最优节点的适应值。该指标反映了节点集合中最优节点适应值经平滑处理后的变化情况，描述了节点的进化能力和GA 搜索能力。

式（16）中，b的理想值miny=y*，由于|y-b|=a＞0 时，Fit(y)=0.5，故在理想情况下，α是适应值为0.5。α、β是阈值参数，一般情况下α取值为[0.5,1.5]，β取值为[1.5,2.0]。

利用GA 思想可以通过改变遗传算子改善簇内结构，从而优化了网络资源，抑制了节点能量的开销，达到了延长网络生存周期的目的。其主要原因在于在GA 算法中采用了可控制阈值参数改变分簇结构，以保持簇内节点的能量的均衡，这样可以避免大量节点由于能量消耗过快而导致的网络瘫痪，同时也克服了由于收敛速度过快而导致收敛于某一局部的极值点，而出现的早熟现象。当某簇内成员节点si和邻居节点sj由竞争关系（剩余能量、与簇首之间的距离）进入下一周期，由式（16）计算出si和sj适应值，即Fit(si)和Fit(sj)，当Fit(sj)-Fit(si)＜0 时，sj直接进入下一周期；否则，将si带入下一周期，采用上述过程可以将某簇内所有成员均遍历一次后，保证簇内所有成员能量的均衡，进一步避免了算法过早进入局部最优解的可能性。

2 覆盖质量与OCC-CT 算法分析

2.1 有效覆盖分析

对于移动目标而言，其所行走轨迹与传感器节点所覆盖形成的区域均显现出不规则形状。为了研究问题的方便，本文采用正方形区域加以说明和计算。计算正方形监测区域内的传感器节点期望值和随机选择k个覆盖期望值均可以依托概率相关理论知识。

定理1传感器节点的覆盖率为p，对移动目标节点完成N次覆盖后，该传感器节点覆盖期望值为E(X)=[1-(1-p)N]p-1。

证明设X为传感器节点首次覆盖移动目标节点时的转换次数，即X∈[1,2,…,N]，当X=k时，存在1 ≤k≤N-1 时，表示传感器节点在N-1 次前并没有覆盖移动目标节点，因此X的分布密度函数为：

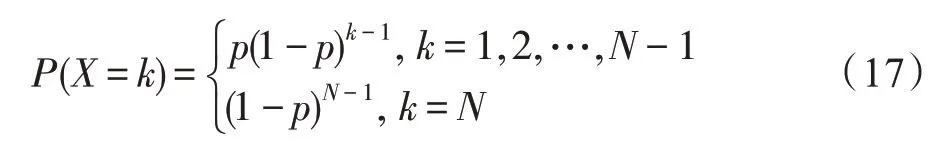
计算式（17）可得：

即：

将式（20）代入式（18），可得：

证明完毕。

推论1传感器节点的覆盖率为p，传感器节点首次完成对移动目标节点覆盖的期望值为：E(X)=1/p，D(X)=(1-p)/p2。

证明依题意可知，在监测区域内任意传感器节点的覆盖率为p，未被传感器节点所覆盖的概率为1-p，令q=1-p，可得传感器节点首次覆盖移动目标节点的期望值为：

覆盖问题的研究本质是要在兼顾感知、通信和连通前提下，监测区域上节点部署时使用的节点数量少，即重复最少的无盲区覆盖。在上述分析中，节点覆盖的物理模型应因不同的物理空间而取不同的形式（如：物理参数），才能够使监测区域上节点部署时在保证无盲区覆盖的前提下使用的节点数量最少[25-27]。因此，本文引入了定理2 和推论2。

定理2在面积为A监测区域内，随机从节点集合中选择k个传感器节点，其覆盖期望值满足：

证明根据定义1 可知，在监测区域内，任意传感器节点的覆盖率为：

由于传感器节点感知半径服从于正态分布(R0,σ2)，R0表示为均值，σ2为方差。对于移动目标节点而言，其被覆盖到的覆盖率为：

计算可得：

化简式（28）可得：

化简式（29）可得：

由于传感器节点在工作中彼此之间相互独立，根据概率理论中独立性质可知，移动目标节点被k个传感器节点所覆盖的期望值为：

证明完毕。

为了减少网络延时，以最大限度提高网络生存周期，在覆盖过程中尽量要用最少节点完成最大面积的覆盖，因此，本文引入了推论2。

推论2完成监测区的有效覆盖，节点最少数量为：

证明给定一个非常小的正整数ε=10-5，对于任意传感器节点覆盖期望值均大于ε可得：

对式（32）两边取对数，可得：

求k：

即：完成监测区域内有效覆盖时，所需最少传感器节点数量为：

证明完毕。

2.2 成簇分析

分簇的目的在于将监测区域内所有传感器节点划分成地位等同的若干相邻域。每个簇内，均由一个主簇首节点和若干个簇成员节点组合而成。低一级网络的簇首节点是高一级网络中的簇成员节点，由最高层的簇首节点和网关节点通信。在分簇拓扑管理结构中，网络内部节点可能划分为簇首节点和簇成员节点。簇首节点是按照某种算法或规则选举出来的，用于控制与管理簇成员节点，协调簇内各类任务，完成簇内数据收集和融合的指挥中心。在经过N轮周期，簇首节点要按照某种算法进行重新选举，以保证簇首节点有足够能量完成上述操作。在分簇过程中，难免会出现节点分配不均匀现象，这样就形成了冗余节点存在。当移动目标节点通过工作冗余节点时，必然产生大量的冗余数据，对簇内节点之间通信造成影响。本文就非对称性链路的双通信机制的研究引入了定理3 和定理4。

定理3删除非对称性链路后，子图Gs连通性保持不变。

证明依据题意可知，图Gs是图G的子图。则∀sj∈C(hi)，hi→sj，即hi与sj之间互相可达。假设d(hi,sj)＜R(hi)和d(hi,si)＞R(sj)，则在sj与hi之间存在一条有向路径l=sj→sl→…→sk→hi。由于簇内成员节点的同构性，si→sj⇒sj→si，因此sk→sl→…→sj。由于R(hi)≥R(sk)，sk→hi⇒hi→sk。因此，可得到hi→sk→sl→…→sj。即删除有向边(hi,si)，也不会影响hi与sj之间的双向连通性。

证明完毕。

定理4当m个移动目标节点经过某簇时，至少存在一条路径，使得m个目标节点所移动的最优路径的概率Pr(¬Pm) 大于或等于1-(1-cm-1p)S，其中，，且C=(1-ρ)L。

证明当且仅当，设从源节点到目的节点的所构成的边集为(k,l)，有限多的路由路径为u，则：

因为Δτkl≥0 且ρ＞0，对于从源节点到目的节点所构成的边集而言，即τkl的值在m+1 周期相同的，如果常数C＞0，则：

由式（37）和式（38）计算可得：

λkl在m+1 周期与m周期是相同的，因此，使用递归计算法可以得到式（40）：

在不失一般性的条件下，假定期望值ηkl(u)可以使用Γ=1 的方法被规范化，即对所有路由边集(k,l)及全局进行优化，可得：

由遗传算法的转移概率公式计算节点r∉u时，满足不等式条件为：

由式（36）和式（43）可得：

由于节点之间相互独立，由概率理论相关知识可得：

证明完毕。

2.3 算法描述与实现

本文OCC-CT 算法是传感器节点建立在传感器节点协同覆盖基础上，将所有传感器节点划分成若干个簇，并以节点能量较高，计算能力较强，距离Sink节点较近的节点充当簇首节点。网络运行的初始阶段，由于每个传感器节点能量均等，成员节点首先向簇首节点发送一个“Coverage”消息，当簇首节点成功接收后，开辟一定存储空间，构建存储链表，并将收集到的消息存放在该链表中，其中“Coverage”消息中包含了发送节点的ID 信息和当前覆盖特性以及该节点当前的位置信息和覆盖期望值等。经过一轮或几轮周期后，簇首收集完成本簇的数据信息之后，对本簇所有节点按照能量和距离优先规则进行重新排序，并将新产生的节点序列存储在链表之中，同时对覆盖期望值和能量以及距离较优的传感器节点赋予最高的权值以充当簇首节点；而后，利用单向查找算法在链表中查找满足下一周期覆盖条件的节点，并向该成员发送“Notice”消息，以调度该节点对移动目标节点的覆盖。本文OCC-CT 算法分为七个步骤：

步骤1根据式（23）和式（24）节点的协同特性对每个传感器节点的覆盖期望值进行计算以确定分簇结构。

步骤2簇首节点建立链表，接收成员节点发送的“Coverage”消息。其中包含了该成员节点的ID 和覆盖特性以及位置消息和覆盖期望值等信息。

步骤3经过多轮周期后，簇首节点依据式（29）和式（31）对存储在链表中的节点按照覆盖期望值和能量大小进行排序，同时对覆盖期望值和能量以及距离较优的传感器节点赋予较高的权值。

步骤4簇首节点在链表中查找符合下一周期覆盖条件的传感器节点，并做以标注；同时利用式（43）选举出下一轮的簇首节点。

步骤5当簇首完成上述操作后计算该节点是否满足下一周期的覆盖条件；如果满足，向该节点发送“Notice”消息，该节点接收到“Notice”消息后启动感知模块完成对移动目标节点的覆盖；否则转入步骤2。

步骤6当移动目标节点被k个节点所覆盖时，簇首节点重新在链表中进行遍历，查找满足覆盖条件的节点，并返回步骤5；否则执行步骤7。

步骤7当移动目标节点离开本簇时，由簇首节点发送消息给相邻簇的簇首节点，重新开始下一周期的覆盖，并返回步骤1，直到移动目标节点被传感器节点完全覆盖。

3 体系评估与分析

为了进一步验证本文OCC-CT算法的稳定性和有效性，本文仿真工具借助于Matlab2013与文献[11-13]在网络覆盖率、网络生存周期以及网络能量开销等方面进行对比实验，仿真参数如表1 所示。

Table 1 Parameter list表1 参数列表

图2 至图4 给出了不同时间下簇首与簇成员的分簇结构示意图。从图中可以看出，不同时间下，簇首与簇成员所形成的簇是不同的。本文采用了动态参数为α=0.5，β=1.5，λ=1.2，同时本文考虑到簇首与簇成员节点之间的距离关系以及簇首节点与基站之间的距离关系，所选择节点更趋向于离基站较近和节点能量较高的节点作为簇首节点，这样就可以有效地减少簇成员节点在传输数据时的能量消耗问题。本文OCC-CT 算法依据节点在链表中的排序以及权值大小，随机选举多个节点作为簇首节点，簇内成员节点个数也显现随机性，这样可以保证簇的覆盖范围较为均衡，平衡了成员节点在覆盖过程能量不均衡等问题。而文献[10]则是利用主副双簇头管理方式。在竞争簇首时，由于成簇原因较为复杂，NDADA（node deployment，assignment method with data association attributes）算法采用主簇头位于簇中心，以快速收集数据；副簇头位于基站较近位置，以便于将主簇头发来的数据快速传输给基站，但文献[10]并未考虑簇内节点能量均衡问题，导致簇内节点能量消耗过快。

Fig.2 t=300 s,clustering structure of cluster head and member nodes图2 t=300 s，簇首与成员节点分簇结构

图5 和图6 以及图7 和图8 给出的是300 m×300 m 和600 m×600 m 监测区域不同参数下，传感器节点数量与网络覆盖率比对示意图。本文选取了四组不同参数，分别为：（α=0.7,β=1.8,λ=1.2），（α=0.5,β=1.5,λ=1.0），（α=0.9,β=2.0,λ=1.5），（α=0.6,β=1.6,λ=1.3）。从上述四个图中可以看出，网络覆盖率与传感器节点数量显现出正比现象，即：网络覆盖率随传感器节点数量递增而增加。通过比对可知：本文OCC-CT 算法在任意传感器节点数量下的网络覆盖率均高于其他三种算法。在图5 中，当传感器节点数量为90 时，本文OCC-CT 算法的网络覆盖率达到了60%和52%，而其他三种算法的网络覆盖率分别为48%、44%和34%；当传感器节点数量为130时，本文OCC-CT 算法网络覆盖率为92%、80%，其他三种算法的网络覆盖率为74%、68%和47%，其本文OCC-CT 算法平均网络覆盖率为86%，高于TMLBSs算法0.12，MWSAC算法0.18和NDADA算法0.39。在图6 中，在传感器节点数量为90 时，本文OCC-CT 算法的网络覆盖率达到了72%和64%，而其他三种算法的网络覆盖率分别为51%、47%和42%；当传感器节点数量为130时，本文OCC-CT算法网络覆盖率为98%、90%，其他三种算法的网络覆盖率为79%、76%和67%，其本文OCC-CT算法平均网络覆盖率为94%，高于TMLBSs 算法0.15，MWSAC 算法0.18 和NDADA算法0.27。综合上述分析，在参数为（α=0.7,β=1.8,λ=1.2），（α=0.5,β=1.5,λ=1.0）时，本文OCC-CT算法网络覆盖率平均高于其他三种算法网络覆盖率为0.23；在参数为（α=0.9,β=2.0,λ=1.5），（α=0.6,β=1.6,λ=1.3）时，本文OCC-CT 算法网络覆盖率平均高于其他三种算法网络覆盖率为0.20。

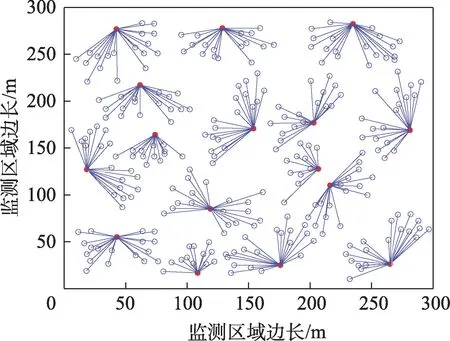
Fig.3 t=500 s,clustering structure of cluster head and member nodes图3 t=500 s，簇首与成员节点分簇结构

Fig.4 t=800 s,clustering structure of cluster head and member nodes图4 t=800 s，簇首与成员节点分簇结构

Fig.5 Comparison of network coverage rate and number of nodes under different parameters in 300 m×300 m图5 300 m×300 m，不同参数下的网络覆盖率与节点数量比对

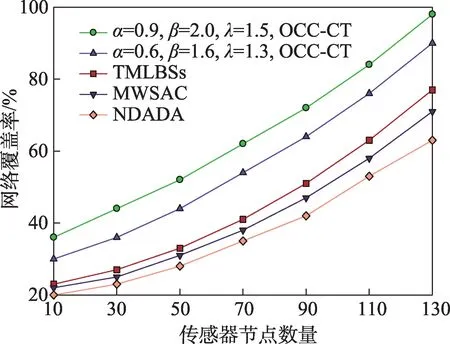
Fig.6 Comparison of network coverage rate and number of nodes under different parameters in 300 m×300 m图6 300 m×300 m，不同参数下的网络覆盖率与节点数量比对

图9 和图10 以及图11 和图12 给出的是300 m×300 m 和600 m×600 m 监测区域不同参数下，网络运行时间与网络覆盖率比对示意图。本文选取了四组不同参数，分别为：（α=0.7,β=1.8,λ=1.2），（α=0.5,β=1.5,λ=1.0），（α=0.9,β=2.0,λ=1.5），（α=0.6,β=1.6,λ=1.3）。从图9 和图11 可以看出，随着网络运行时间的增加，网络覆盖率也随之增加。当网络运行时间达到300 s 和700 s 时，四种算法的网络覆盖率均达到平衡状态，但本文OCC-CT 算法的网络覆盖率要高于其他三种算法。从图9 中可以看出，当网络运行时间为300 s 时，本文OCC-CT 算法网络覆盖率达到了99%、92%，而其他三种算法的网络覆盖率分别为：77%、72%和62%；网络运行时间为300 s 时，本文OCC-CT 算法平均网络覆盖率为96%，分别高于其他三种算法0.19、0.24 和0.34；从图11 中可以看出，当网络运行时间为700 s 时，本文OCC-CT 算法网络覆盖率达到了99%、86%，而其他三种算法的网络覆盖率分别为：78%、70%和65%；网络运行时间为700 s时，本文OCC-CT 算法平均网络覆盖率为93%，分别高于其他三种算法0.15、0.23 和0.28；图10 和图12给出的是在监测300 m×300 m，600 m×600 m 不同参数下的网络运行时间与网络覆盖率比对示意图。图10 和图12 采用的参数为（α=0.9,β=2.0,λ=1.5），（α=0.6,β=1.6,λ=1.3），从图中可以看出，随着网络时间的推移四种算法的网络覆盖率均处于平稳状态，但本文OCC-CT 算法网络覆盖率要高于其他三种算法。在图10中，当网络运行时间为400 s 时，本文两组参数均达到了100%，而其他三种算法均低于该值，分别是83%、76%和68%，平均值高于其他三种算法分别为0.17、0.24 和0.32；在图12 中，当网络运行时间为800 s 时，本文OCC-CT 算法分别高于其他三种算法分别为0.13、0.22和0.27。综合上述分析结果可以看出，本文OCC-CT 算法在传感器节点数量与网络覆盖率和网络运行时间与网络覆盖率对比实验中，均高于其他三种算法，从而进一步说明了本文OCC-CT 算法具有较强稳定性和有效性。

Fig.7 Comparison of network coverage rate and number of nodes under different parameters in 600 m×600 m图7 600 m×600 m，不同参数下的网络覆盖率与节点数量比对

Fig.8 Comparison of network coverage rate and number of nodes under different parameters in 600 m×600 m图8 600 m×600 m，不同参数下的网络覆盖率与节点数量比对

Fig.9 Comparison of network coverage rate and running time under different parameters in 300 m×300 m图9 300 m×300 m，不同参数下的网络覆盖率与运行时间比对

Fig.10 Comparison of network coverage rate and running time under different parameters in 300 m×300 m图10 300 m×300 m，不同参数下的网络覆盖率与运行时间比对

图13 至图16 给出的是300 m×300 m 和600 m×600 m 监测区域不同参数下，传感器节点数量与网络生存周期比对示意图。从图13 和图14 中可以看出，随着传感器节点数量的增加，网络生存周期也随之增加，从增加的幅度可以看出，本文OCC-CT 算法的增幅明显高于其他三种算法。在图13中，当传感器节点数量为90 时，本文OCC-CT 算法网络生存周期分别为525 s、465 s，而其他三种算法的网络生存周期分别为375 s、335 s 和260 s，其本文OCC-CT 算法网络生存周期平均值分别高于其他三种算法为120 s、160 s和235 s；而在图14 中，当传感器节点数量为70 时，本文OCC-CT 算法网络生存周期分别为615 s、500 s，而其他三种算法的网络生存周期分别为405 s、345 s 和315 s，其本文OCC-CT 算法网络生存周期平均值分别高于其他三种算法152.5 s、212.5 s 和242.5 s。其主要原因在于本文OCC-CT 算法采用的是对移动目标节点局部连续覆盖方法，在覆盖过程中利用遗传算法动态参数的可控性对网络生存周期和网络覆盖率进行优化控制，以达到网络资源的最佳配比结果；而TMLBSs 算法和MWSAC 算法则采用的是对移动目标节点连续覆盖方法完成对移动目标节点的覆盖控制，而没有考虑当移动目标节点远离某簇后，该簇的工作状态，NDADA 算法采用的是一种连续全局覆盖方法对移动目标节点的连续覆盖，也就相当于对整个监测区域的完全覆盖，并没有考虑网络能量的消耗问题。图15和图16的工作原理与图13和图14相似。

Fig.11 Comparison of network coverage rate and running time under different parameters in 600 m×600 m图11 600 m×600 m，不同参数下的网络覆盖率与运行时间比对

Fig.12 Comparison of network coverage rate and running time under different parameters in 600 m×600 m图12 600 m×600 m，不同参数下的网络覆盖率与运行时间比对

Fig.13 Comparison of network lifetime and number of nodes under different parameters in 300 m×300 m图13 300 m×300 m，不同参数下的网络生存周期与节点数量比对

Fig.14 Comparison of network lifetime and number of nodes under different parameters in 300 m×300 m图14 300 m×300 m，不同参数下的网络生存周期与节点数量比对

图17 至图20 给出的是300 m×300 m 和600 m×600 m 监测区域不同参数下，网络运行时间与网络能耗比对示意图。从图中可以看出，随着网络运行时间增长，四种算法网络能耗均有所下降，但本文OCCCT 算法网络能耗下降的幅度较少，而NDADA 算法网络能耗下降幅度较大。现以图17 为例进行分析，当网络运行时间为400 s 时，本文OCC-CT 算法剩余能量为585 J 和555 J，而其他三种算法剩余能量为535 J、515 J 和510 J，其本文OCC-CT 算法剩余能量平均值分别高于其他三种算法35 J、55 J 和60 J；在图18 中，当网络运行时间为500 s时，本文OCC-CT 算法剩余能量为610 J 和560 J，而其他三种算法剩余能量为560 J、520 J 和485 J，其本文OCC-CT 算法剩余能量平均值分别高于其他三种算法25 J、65 J 和100 J；综合上述分析结果，本文OCC-CT 算法网络生存周期和网络能耗均明显高于其他三种算法，从而验证了本文OCC-CT 算法的有效性和适应性。

Fig.15 Comparison of network lifetime and number of nodes under different parameters in 600 m×600 m图15 600 m×600 m，不同参数下的网络生存周期与节点数量比对

Fig.16 Comparison of network lifetime and number of nodes under different parameters in 600 m×600 m图16 600 m×600 m，不同参数下的网络生存周期与节点数量比对

Fig.17 Comparison of running time and network energy consumption under different parameters in 300 m×300 m图17 300 m×300 m，不同参数下的网络运行时间与网络能耗比对

Fig.18 Comparison of running time and network energy consumption under different parameters in 300 m×300 m图18 300 m×300 m，不同参数下的网络运行时间与网络能耗比对

Fig.19 Comparison of running time and network energy consumption under different parameters in 600 m×600 m图19 600 m×600 m，不同参数下的网络运行时间与网络能耗比对

Fig.20 Comparison of running time and network energy consumption under different parameters in 600 m×600 m图20 600 m×600 m，不同参数下的网络运行时间与网络能耗比对

4 总结

基于无线传感器网络在覆盖过程出现的节点能量问题和数据冗余对通信链路的影响，本文提出了一种带有可控阈值的优化协同覆盖算法。本文OCCCT 算法首先利用覆盖模型对移动目标节点进行了分析，同时给出了覆盖模型的具体分析方法。其次，本文对覆盖期望值进行了分析和计算。给出了对移动目标节点完成N次覆盖后，该传感器节点覆盖期望值计算方法以及完成对移动目标节点所需覆盖的最少传感器节点数量的计算过程以及最优路径选择的概率计算方法。再次，本文给出了OCC-CT 算法描述过程和实现方法以及本文OCC-CT 算法复杂度的相关说明。最后，本文利用仿真软件对网络成簇结构、网络覆盖率、网络生存周期以及网络能耗四方面进行了相关实验并给出了仿真实验对比步骤和方法，以此进一步地说明本文OCC-CT 算法具有较高的有效性和稳定性。