地震-列车移动荷载耦合作用下高铁路基振动特性研究

高 盟, 彭晓东, 李大勇, 石传志, 陈 昊

(1. 山东科技大学 山东省土木工程防灾减灾重点实验室, 山东 青岛266590;2. 山东科技大学 土木工程与建筑学院, 山东 青岛 266590)

0 引言

我国高速铁路的大规模建设及列车运营班次的增加,使得列车运行时遭遇地震的几率大幅提高。列车运行过程中遭遇地震极易引发脱轨事故[1-2],给人们的生命财产安全带来了严重威胁。因而有关轨道和路基的振动特性成为重要研究课题,研究将有利于解决列车遭遇地震时的脱轨问题,同时可为高速铁路地震预报预警系统的优化提供理论指导。

上述问题主要涉及两个方面,一方面是列车移动荷载,另一方面是地震荷载。有关列车移动荷载下铁路路基与轨道的动力响应已有较多研究成果,主要分为试验研究、数值计算和现场实测三大类。牛婷婷等[3]建立大比例尺模型试验,分析了桩网复合地基的动力响应特性,研究了加载频率、加载幅值及振次等因素对复合地基振动速度的影响;蒋红光等[4]在全比尺试验的基础上,分析移动荷载下轨道路基的动力响应,提出高速铁路路基加速试验的设计准则;Alshear等[5]建立1∶3缩尺模型试验,利用多个作动器模拟移动荷载效应,得到加速度、位移等结果,实验结果表明路基动力特性与列车移动荷载循环次数密切相关。在数值计算方面,Eason[6]研究了移动点荷载作用下三维半空间的稳态响应,采用积分变换的方法求解基本方程;Yang等[7]用2.5维有限元方法分析了考虑离散轨枕支撑时轨道和地基在列车荷载作用下的动力相互作用;Thach等[8-9]利用有限元软件,分析了列车移动荷载作用下加固路基与天然地基的动力响应;罗震等[10]建立梁-板-板有限元模型,计算不同运行速度下轨道的动力响应,分析车速对轨道振动特性的影响;Takemiya等[11]考虑列车的几何形状和运行速度,模拟瑞典高速列车X-2000运行引起附近软土地基的振动传播情况;高广运等[12]基于Biot波动方程和边界条件,利用Fourier变换和Galerkin法推导出2.5维有限单元方程,研究列车荷载作用下地面振动特性;巴振宁等[13]推导了移动荷载作用下饱和层状地基的动力格林函数,建立2.5D边界元数值计算模型,分析得出了列车移动荷载引起的饱和地基的动力响应规律。在现场实测方面,高盟等[14]对青岛地铁3号线和上海地铁10号线进行了现场实测,分析了列车移动荷载作用下地铁运行的振动响应值;聂志红等[15]对秦沈客运专线进行了现场测试,得到了不同车速下的动应力与加速度值,分析了它们在基床表层的分布规律;张晓磊等[16]开展京沪高铁段现场测振试验,分析列车速度在250～350 km/h时高速铁路路基的振动频域与振幅并基于加速度对场地振动水平进行评价。

目前,关于地震-列车移动荷载耦合作用下铁路路基与轨道的动力响应鲜有研究。张铭哲[17]基于ANSYS计算软件,建立四线高铁连续桥计算模型,研究地震荷载和移动荷载共同作用下高铁连续梁桥的动力响应,提出高铁连续梁桥动力性能计算方法;韩艳等[18]基于桥梁结构动力学和车辆动力学理论,编制仿真计算程序,通过控制车速和不同地震力大小,分析了斜拉桥在地震和列车荷载同时作用下的振动特性;郜新军等[19]基于有限元分析软件,建立车-桥耦合分析模型,研究了不同地震波入射角度及车速对桥梁动力响应的影响;安会峰等[20]采用有限元建模软件,建立钢桁架桥模型,研究了地震荷载、列车荷载及两者共同作用下钢桁架桥的加速度时程变化规律。以上研究均涉及的是桥梁领域中高速铁路路基的振动特性研究,然而桩承式路基与自由式路基在高速铁路中也占有很大比重,因此研究地震-列车荷载共同作用下桩承式路基与自由式路基的振动特性是十分必要的。

针对上述研究现状,本文基于轨道结构-路基-地基动力相互作用理论,采用ABAQUS有限元计算程序建立考虑地震-列车移动荷载耦合输入的轨道结构-路基-地基三维动力学模型,研究了地震-列车移动荷载耦合作用下高速铁路轨道与路基的振动响应问题。

1 数值模型建立与分析验证

1.1 模型建立与参数选择

根据文献[21]建立轨道结构-路基-地基三维有限元模型。模型纵向长度为52 m,地基表面宽度为52 m,模型高度为25.456 m。模型系统由钢轨-扣件-轨道板-CA砂浆层-底板-基床表层-基床底层-路基本体-桩-地基组成。其中,钢轨采用60 kg·m-1标准钢轨,轨距为1.435 m;扣件支点间距为0.65 m;钢轨与轨道板之间的联结件等效为线弹性体,不考虑联结件非线性因素,联结件采用弹簧-阻尼单元进行模拟[22],扣件刚度的横向、垂向及纵向等效刚度分别为37.5、25、37.5 kN·m-1,阻尼系数分别为30、37.5、30 kN·s·m-1;轨道板、CA砂浆层、路基和地基均采用8结点实体单元。由于轨道板与基床表面、路基底面与土体之间的滑动均相对较小,施加摩擦特性为“罚”的切向作用,同时轨道板与基床表面、路基本体底面与土体设置Tie接触,通过Tie接触[23]保持各接触面之间的变形协调。具体几何模型与网格划分如图1所示。

图1 有限元计算模型Fig.1 Finite element computing model

本模型轨道板采用CRTSⅠ型板式无砟轨道,轨道结构从上至下依次是钢轨、轨道板、CA砂浆层和底板。在路基下方设置群桩,桩长为10 m,直径为0.8 m,桩间距为2 m,采用正方形布置。本文在整个结构中设置4个监测点,分别是监测点1-轨道,监测点2-基床表层,监测点3-路肩边,监测点4-路基。模型剖面示意如图2所示。

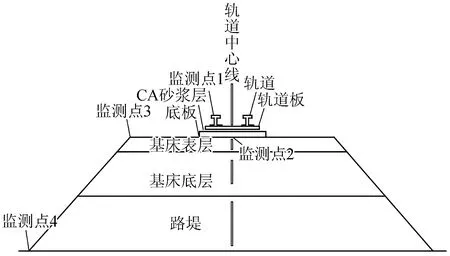
图2 有限元计算模型剖面示意图Fig.2 Profile of finite element calculation model

参考文献[24],计算模型各组成部分均采用弹性本构,模型边界采用三维黏弹性人工边界。计算参数列于表1。

表1 有限元模型计算参数

1.2 地震荷载

对于地震波的施加,较为合理的方法是将地震波转化为边界节点上的等效荷载参考文献[25],将地震波加速度直接从模型底部输入。地震波采用Imperial Valley地震波,抗震设防烈度设为7度,根据《铁路工程抗震设计规范(GB50111-2006)》[26]中抗震设防烈度和地震动峰值加速度值的对应表,列于表2,将地震波峰值调整为0.1g,其水平方向加速度时程曲线如图3所示。取地震加速度时程曲线2～3.6 s加速度从模型底部输入,经计算,此时地面的加速度峰值约为0.13g,相当于烈度为7度的地震。

表2 抗震设防烈度和地震动峰值加速度值Ag对应表

图3 Imperial Valley 地震加速度时程曲线Fig.3 Acceleration time history of Imperial Valley wave

1.3 列车移动荷载

列车在运行过程中,轨道所受到的列车荷载包括3部分:移动的动荷载、固定作用点的动荷载、移动的轴荷载[27]。本文通过编制DLOAD子程序,将列车移动荷载与ABAQUS程序联立,进而实现列车移动荷载的施加。列车被模拟为一系列轴重荷载组成,边学成等[28]将列车产生的连续轴重荷载用下式表示:

(1)

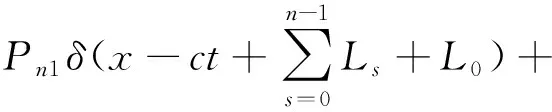
(2)

式中:Pn1和Pn2分别表示车厢前轮和后轮轴重;Ln为车厢长度;L0为从第1节车厢前某一个设定的测量点开始的距离;an和bn为轴之间的距离。

列车选用CRH3型动车组,动车组长度约200 m,列车轴重为17 t,中间车车辆长度为25 m,车辆定距为17.375 m,转向架的固定轴距为2.5 m,两辆车之间轴距为4.5 m。列车荷载示意如图4所示。

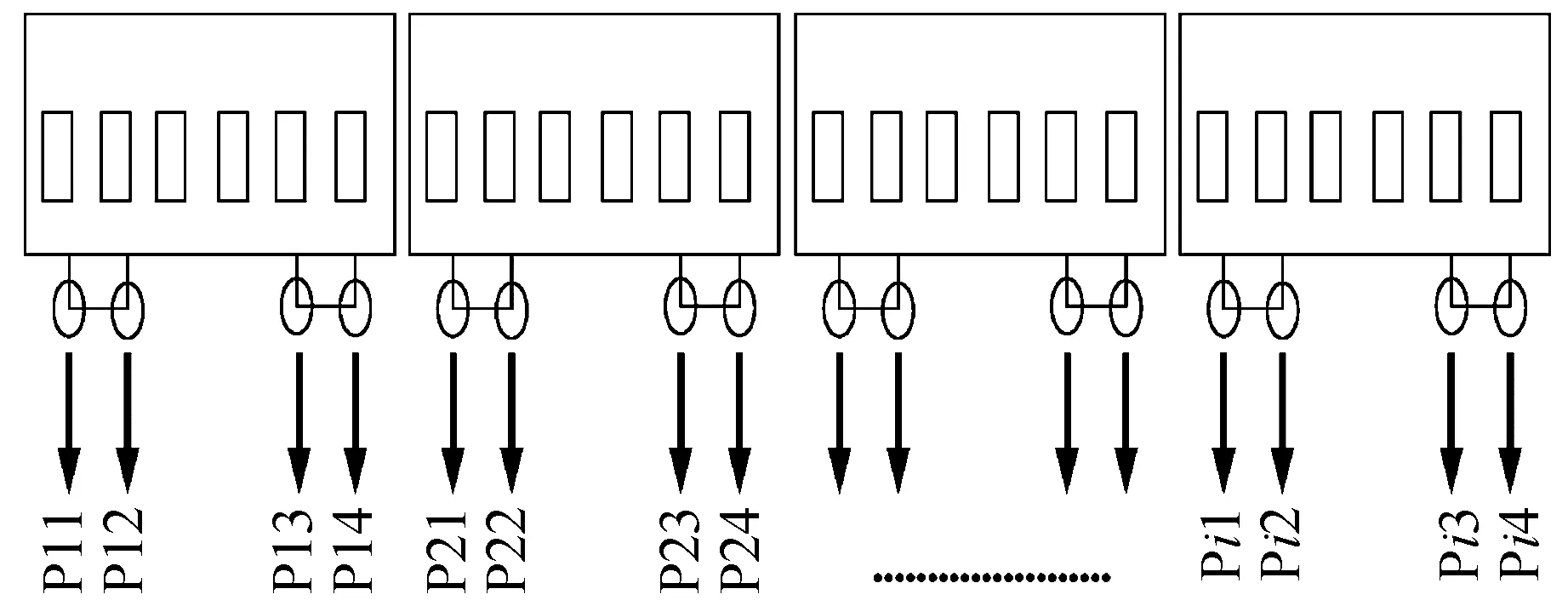
图4 列车轴重荷载分布图Fig.4 Distribution of train wheel-axel loads

1.4 计算模型验证

为了验证模型有效性,本节建立了与参考文献[29]与文献[6]相同计算参数的模型,得到基床表层中心线处水平和竖向归一化振动位移幅值,将该计算结果与文献[29]和文献[6]进行对比(图5)。

根据图5可知,基床表层中心线水平和竖直方向归一化振动位移幅值曲线在列车经过时产生剧烈变化,其余时间产生细微变化,符合客观事实规律,且计算结果与文献[29]和文献[6]计算结果变化趋势高度吻合,计算结果基本一致。但水平方向2.46～2.53 s振动位移幅值与竖直方向2.50～2.53 s、2.57～2.60 s的振动位移幅值存在细微差别,原因是文献[29]和文献[6]为精确的解析解,研究方法不同造成了计算结果产生细微差别。综上分析,本文计算模型具有较高可靠性与有效性。

图5 归一化振动位移幅值Fig.5 Normalized value of vibration displacement amplitude

2 桩承式路基与自由式路基振动特性分析

本文取列车速度为252 km/h,地震波最大加速度为0.1g,列车轴重为17 t,桩承式路基桩径0.8 m,桩长为10 m,桩间距为2 m,路堤高度2 m;分析时间0～1 s设为地震荷载作用,1 s后开始施加列车移动荷载作用,分析时间设为0.6 s。计算轨道与路基的振动位移幅值、加速度时程与频谱曲线,对比分析桩承式路基与自由式路基的振动特性。

2.1 振动位移幅值分析

图6为自由式路基与桩承式路基在各监测点的振动位移幅值对比图。由图可知,桩承式路基与自由式路基的振动位移幅值差别较大,取1.33 s时轨道和路基的振动位移幅值大小,如表3所示。由表3可知,在地震和列车耦合作用下桩承式路基中监测点(路肩边除外)的振动位移幅值皆大于自由式路基。根据已有工作结果分析,在单独施加列车移动荷载或者地震荷载时,桩承式路基的振动位移幅值和加速度皆小于自由式路基。

图6 路基及轨道振动位移振幅对比Fig.6 Vibration displacement amplitude comparison of subgrade and track

表3 自由式路基与桩承式路基位移振幅对比

2.2 加速度时程分析

图7和图8分别为自由式路基与桩承式路基中轨道与路基加速度时程曲线。由图7与图8中(a)、(b)、(c)6幅图可知,列车荷载对轨道加速度影响较大,而地震荷载对轨道加速度影响较小;由图7(d)与图8(d)可知,前1 s内加速度变化较小,1～1.6 s加速度变化剧烈,说明列车荷载对基床表层加速度影响较大,地震荷载对基床表层加速度影响较小;由图7(e)与图8(e)可知,列车荷载对路肩边加速度影响较小;由图7(f)和图8(f)可知,列车荷载对路基坡脚加速度几乎没有影响。自由式路基与桩承式路基各监测点加速度对比分析列于表4。由表4可知,桩承式路基中轨道与路基加速度小于自由式路基加速度,轨道X方向加速度减小6.2%,轨道Y方向减小30.7%,在轨道Z方向减小0.5%,基床表层竖向加速度减小0.9%,路肩边竖向加速度减小50%,路基坡脚竖向加速度减小28.6%。由此可知,桩承式路基对轨道X和Z方向影响较小,但在轨道Y方向有良好的减振作用。桩承式路基对路肩边的加速度影响较大,路基坡脚减振效果也较显著,但是对基床表层影响非常小。基床表层加速度主要是列车移动荷载通过轨道、轨道板和底板直接传递到基床表层,所以受桩承式路基影响较小。总体来说桩承式路基在加速度方面有较好的减震作用。

图7 自由式路基中轨道和路基加速度时程曲线Fig.7 Acceleration time history curve of rail and subgrade in freestyle subgrade

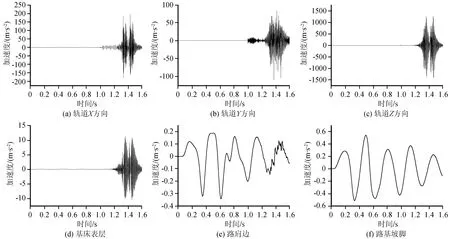
图8 桩承式路基中轨道和路基加速度时程曲线Fig.8 Acceleration time history curve of rail and subgrade in pile-supported subgrade

表4 自由式路基与桩承式路基加速度最大值对比

2.3 加速度频谱分析

图9和图10分别为自由式路基和桩承式路基中轨道与路基加速度频谱曲线。由图可知,轨道主导频率范围为120～160 Hz,属高频振动,另外轨道X方向在40～60 Hz还有一个副主频。基床表层主导频率为120～160 Hz,跟轨道主导频率相同,可以看出基床表层受列车移动荷载影响较大。路肩边和路基坡脚主导频率为0～10 Hz,受地震荷载影响较大。自由式路基与桩承式路基各监测点加速度频谱曲线对比分析列于表5。由表5可知,高速铁路桩承式路基并不会影响路基及路基上方轨道的振动频率,但会改变轨道和路基的振动加速度大小。

图9 自由式路基中轨道与路基加速度频谱曲线Fig.9 Acceleration spectrum curve of rail and subgrade in freestyle subgrade

图10 桩承式路基中轨道与路基加速度频谱曲线Fig.10 Acceleration spectrum curve of rail and subgrade in pile-supported subgrade

表5 自由式路基与桩承式路基频谱曲线对比

3 结论

本文建立轨道结构-路基-地基三维有限元模型,研究了桩承式路基与自由式路基在地震-列车移动荷载耦合作用下的动力响应问题。文中分别以桩承式路基和自由式路基为模型,讨论了在耦合作用下两种路基的振动位移幅值、加速度时程与频谱,并对比分析了两种路基的差异,主要得到了以下四点结论。

(1) 在地震-列车移动荷载耦合作用下,桩承式路基中轨道和路基发生共振,桩承式路基的振动位移幅值大于自由式路基。

(2) 桩承式路基的减振效果在加速度方面具有良好的体现,特别是对轨道X方向、路肩边及路基坡脚处的加速度影响显著,比自由式路基分别减小6.2%、50%、28.6%。

(3) 轨道与基床表层加速度频谱受列车移动荷载影响较大,主要为高频振动,主导频率为120～160 Hz,其中轨道X方向在40～60 Hz内有副主频;路肩边与路基坡脚受地震荷载影响较大,主要为低频振动,主导频率为0～10 Hz。

(4) 在地震-列车移动荷载耦合作用下,高速铁路桩承式路基并不影响路基及路基上方轨道的振动频率,但会影响其振动加速度大小。