基于Python的圆形截面配筋计算方法研究

朱亚萍, 马朋涛

(中交第一公路勘察设计研究院有限公司， 陕西 西安 710075)

1 概述

1.1 Python语言

Python语言于1989年由Guido开发，目前，Python有两个版本影响最为广泛，2.x版及3.x版。该文相关代码都采用3.7版的Python编写。

Python语言的核心包含数字、字符串、列表、字典、文件等常见类型和函数，同时Python还提供了一个很强大的标准库，用于实现系统管理、网络通信、文本处理等额外的功能。而Python更强大之处在于社群为其提供的庞大的第三方模块。这些第三方模块的使用方式与标准库类似，它们的功能覆盖科学计算、Web开发、数据库接口、图形系统多个领域。由于第三方模块可以使用Python或者C语言编写，其他语言也常常将自身的程序库转化为Python模块，因而Python常被用做其他语言与工具之间的“胶水”语言。

该文除了使用Python自身的基本核心和标准库之外，还使用了numpy、pandas、matplotlib等第三方模块。numpy是Python进行科学计算的基础软件包；pandas是一个强大的分析结构化数据的工具集，可以与电子表格(excel)进行数据交换；matplotlib则是一个Python的2D绘图库。这些模块的功能丰富，具体的使用办法该文不赘述。

1.2 圆形截面配筋公式

圆形截面是桥梁下部结构最常使用的截面形式，比如柱式桥墩的墩柱和桩基础。

JTG 3362-2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》于2018年11月1日正式实施，以下简称“JTG 3362”。其在第5、6章中对圆形截面承载能力和裂缝验算的相关内容进行了较大的调整。

根据条文说明JTG 3362第5.3.8条，圆形截面的承载能力计算公式尽管进行了修改，与JTG D62-2004《公路钢筋混凝土及预应力混凝土桥梁设计规范》(简称JTG D62)相比，两者公式推导的基本原理是一致的，不同的简化处理方法，导致不同的表达式。

在JTG D62第6.4条中，钢筋混凝土构件裂缝宽度验算公式进行了调整，同时在JTG D62第6.4.4条和6.4.5条中对圆形截面相关的计算公式进行了调整。

该文对相关计算公式进行分析研究，根据不同的计算模式将公式进行变形，得到相应的计算模型，采用Python语言编写代码加以实现，得到最终所需的截面承载力或配筋。

2 计算公式研究及代码

2.1 圆形截面抗压承载力计算公式

JTG 3362第5.3.8条，沿周边均匀配置纵向钢筋的圆形截面钢筋混凝土偏心受压构件(图1)，其正截面抗压承载力计算应符合下列规定：

(1)

(2)

式中:各参数意义详见JTG 3362。

图1 沿周边均匀配筋的圆形截面

为了方便求解，避免符号冲突，将式(1)、(2)中圆形截面的面积由“A”改为“A0”。同时，令ρ=As/A0，g=rs/r，令：

(3)

由于式(3)中A、B、C、D4个参数只与参数α相关，均可表示为α的函数。这里α的意义与规范一致，对应于受压区混凝土截面面积的圆心角(rad)与2π的比值。为方便起见，在程序中设置了函数A(α)、B(α)、C(α)、D(α)来计算这几个参数。

根据上述定义，式(1)、(2)可以改写为：

γ0Nd≤Nud=(Afcd+Cfsdρ)A0

(4)

γ0Ndηe0≤Mud=(Bfcd+Dfsdρg)A0r

(5)

令:

(6)

(7)

(8)

则式(4)、(5)中的等式部分可进一步改写为：

nu=A+Cρr

(9)

nuer=B+Dρrg

(10)

观察式(6)、(7)、(8)可以发现：nu、ρr、er均为无量纲参数，这样式(9)、(10)所表示的圆形截面承载力公式就更具有一般性意义。

2.1.1 竖向承载力计算

对配筋已知的截面，保持竖向荷载偏心距不变，求截面最大的竖向承载力。按式(9)、(10)可描述为已知ρr、er，求nu。

由式(9)、(10)可得：

(11)

由于ρr、er均为已知，则式(11)为关于α的方程。由于方程中包含关于α的正弦函数项，方程无法直接求解，可以通过试算迭代的方法求解。为了确定求解算法，可以将式(11)的右边看成关于α的函数er(α)，分别取ρr为0.30、0.60、0.90、1.20，绘制er(α)的函数曲线，如图2所示，图中曲线均采用Matplotlib进行绘制。

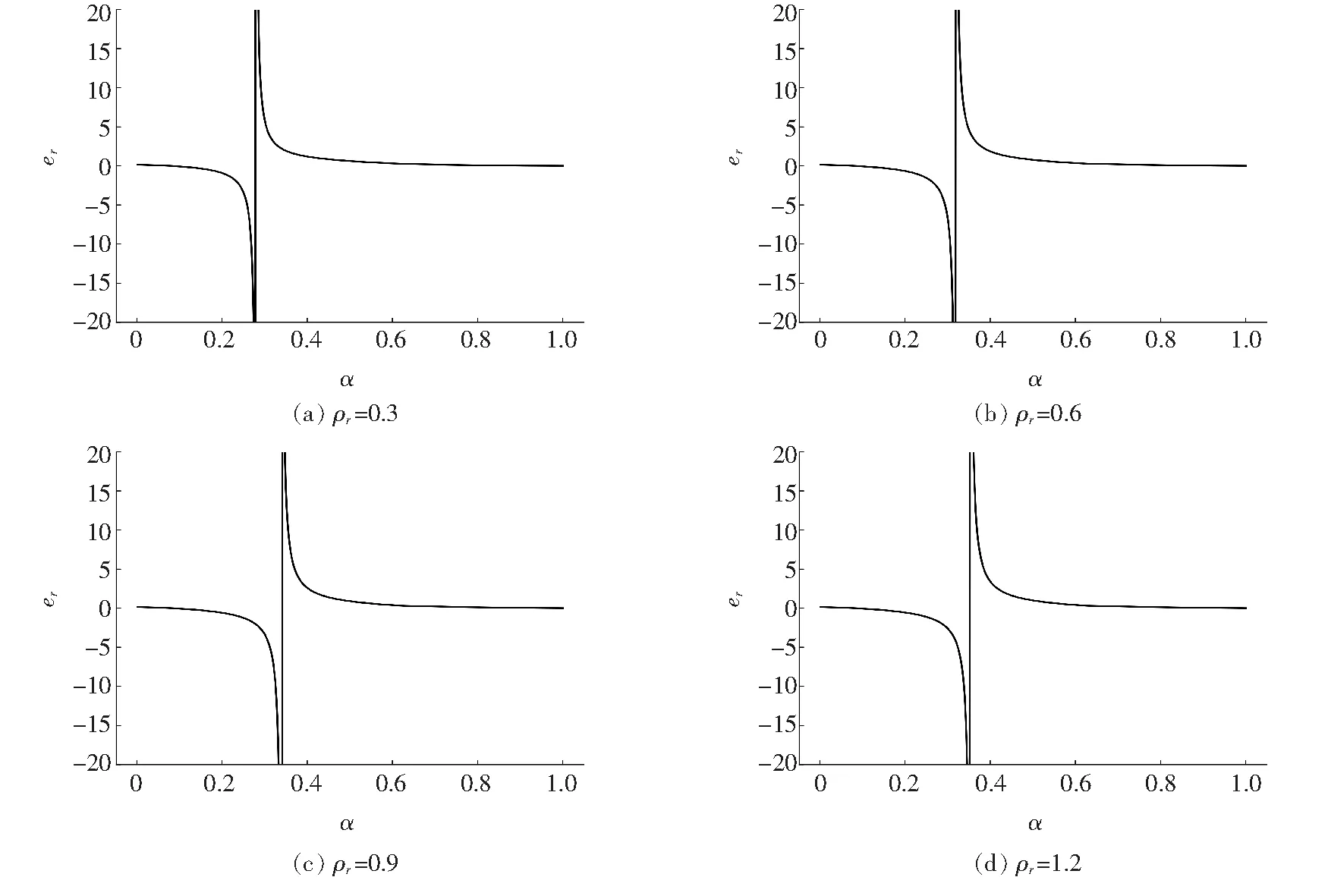
图2 er(α)的函数曲线

由图2可以看出：er(α)为类似双曲函数的曲线，有两条渐近线er=0和α=αasym。

当α<αasym时，er(α)<0；当α>αasym时，er(α)>0。er(α)函数在两段定义域内都是单调递减的，因此可以考虑使用二分法求解。基于er(α)函数的特点，考虑到所求的er值必为正值，因此在迭代过程中需要进行特别的处理。

JTG 3362附录F表F.0.1(表1)中的每个数值均可以采用上述nu()函数进行计算，将计算数值采用pandas模块保存于F01.xlsx文件中(表2)。

与表1进行对比，表2大部分计算值均与规范吻合，很少部分数值误差在万分之一左右。

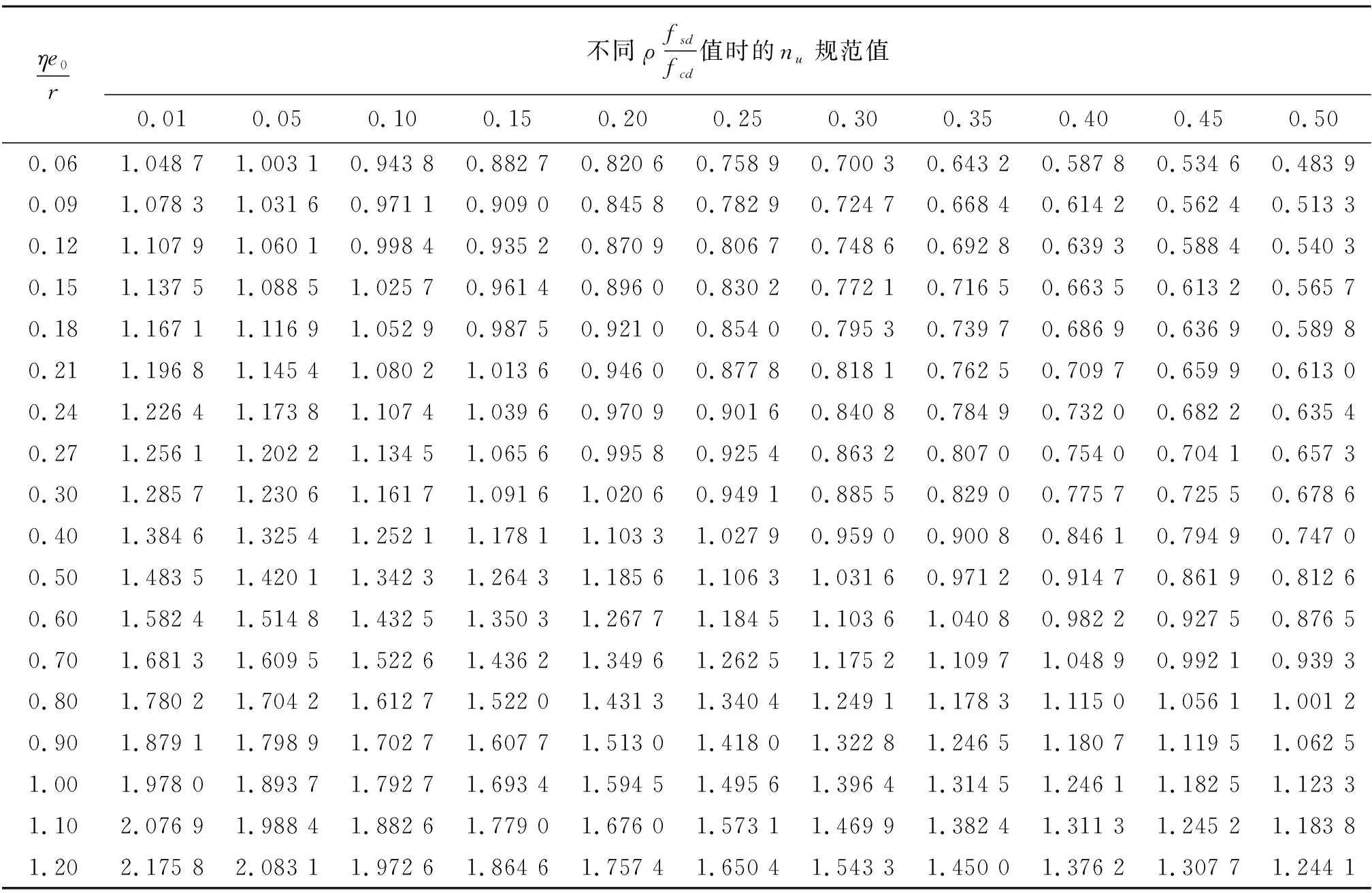
表1 JTG 3362表F.0.1

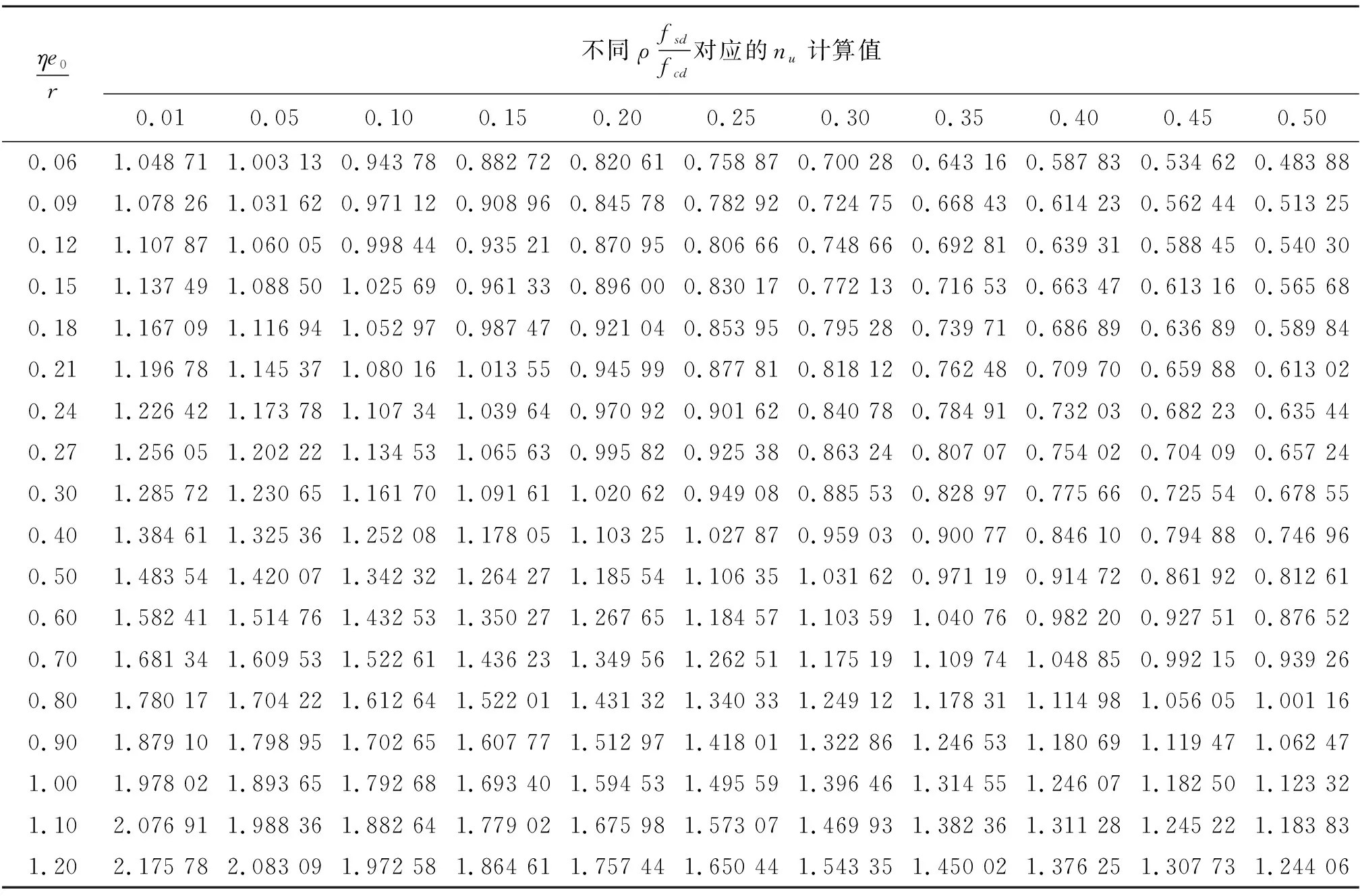
表2 抗压承载能力nu计算值

2.1.2 弯矩承载力计算

对配筋已知的截面，保持竖向荷载不变，求截面承受的最大弯矩。按式(9)、(10)可描述为已知ρr、nu，求er。

由式(9)可知，由于ρr、nu均为已知，可以将式(9)的右边看成关于α的函数nu(α)，分别取ρr为0.30、0.60、0.90、1.20，绘制nu(α)的函数曲线，如图3所示。

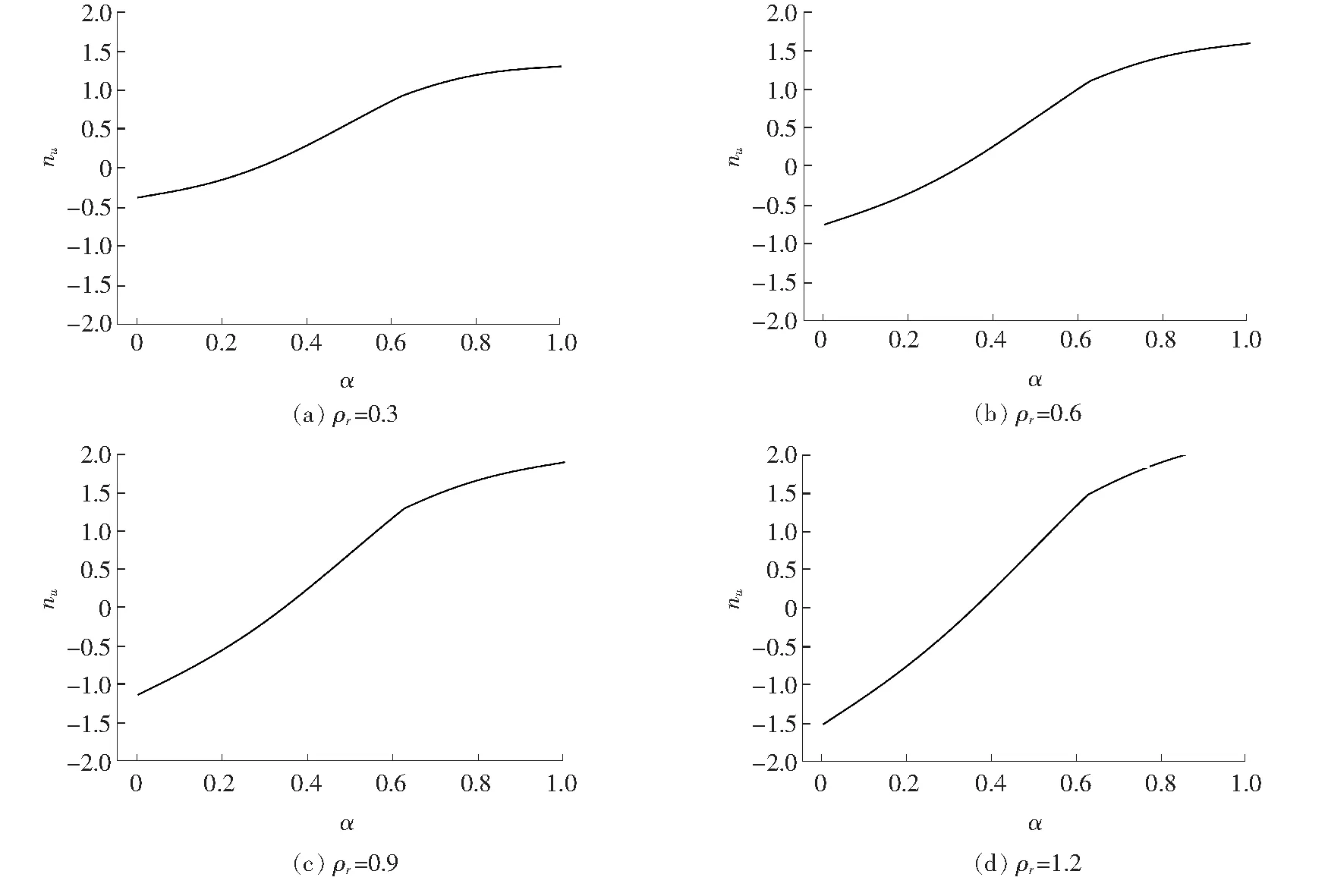
图3 nu(α)的函数曲线

由图3可以看出:nu(α)函数在定义域内是单调递增的，因此可以考虑使用二分法求解。

2.1.3 按承载力计算配筋

作用于圆形截面的轴力和弯矩已知，求截面所需的配筋。按式(9)、(10)可描述为已知nu、er，求ρr。

由式(9)、(10)可知：

(12)

将式(12)代入式(9)得：

(13)

由于er为已知，可以将式(13)的右边看成关于α的函数nu(α)，分别取er为0.01、0.05、0.25、1.25、6.25，绘制nu(α)的函数曲线，如图4所示。

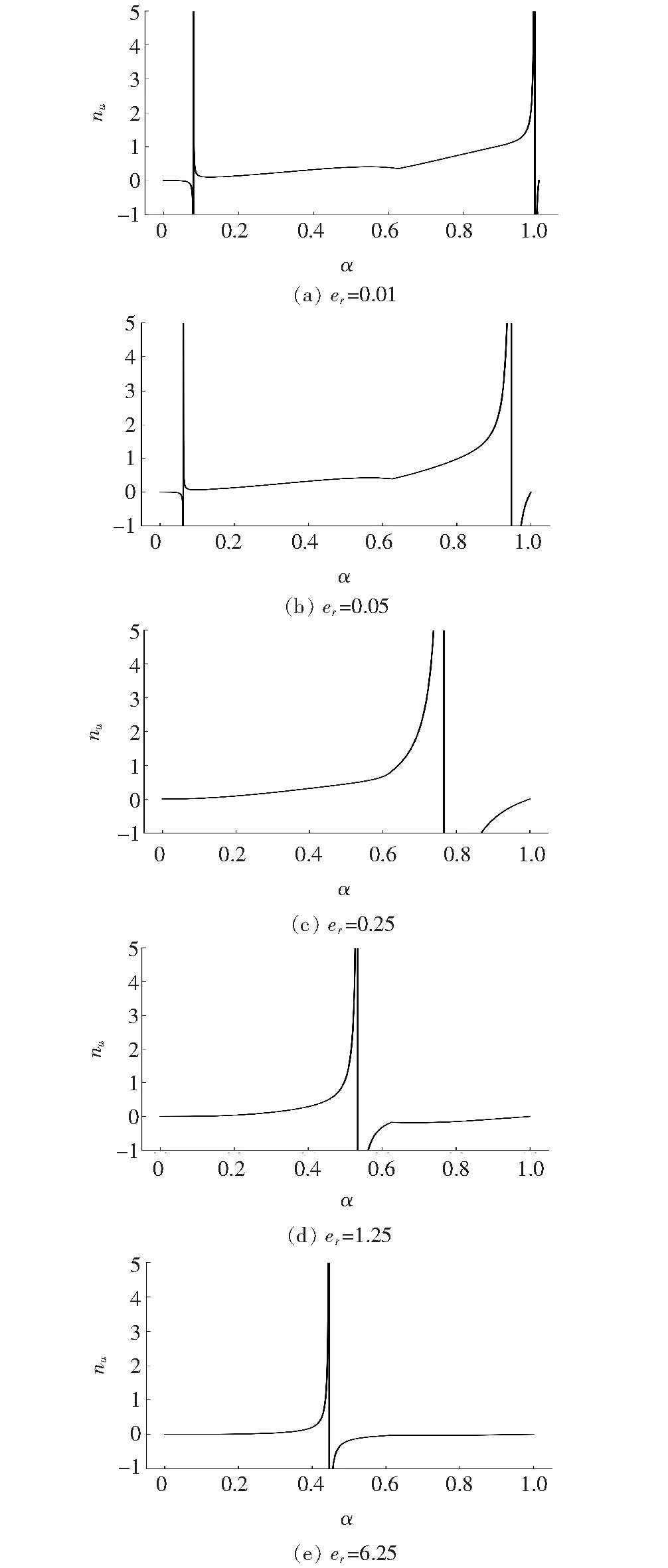
图4 nu(α)的函数曲线

由图4可以看出：nu(α)的函数曲线比较复杂，局部与双曲线类似，存在多组渐近线。考虑nu的取值应为正值，关注nu(α)函数曲线大于0的部分可发现，这部分函数都是单调递增的，还是可以采用二分法进行求解，遇到负值的情况需要特殊处理。

将JTG 3362表F.0.1中的nu、er代入rho_r()函数中，即可验证代码执行的正确性。经过测试，rho_r()函数工作正常，这里不再赘述。

2.2 圆形截面裂缝宽度验算公式

JTG 3362第6.4.3条规定，钢筋混凝土构件的最大裂缝宽度应满足：

(14)

其中：

(15)

(16)

r1=r-2as

(17)

(18)

由于已知截面荷载及配筋，将相关数据代入公式求解裂缝宽度即可。

以下讨论已知截面荷载、根据给定的裂缝宽度计算截面配筋的情形。

令：

(19)

(20)

将As=ρπr2以及式(18)、(19)、(20)分别代入式(15)、(16)，整理得：

(21)

(22)

令：

(23)

将式(22)、(23)代入式(14)得：

(24)

将式(24)整理为关于ρ的方程得：

4.25βrρ3+0.68βrρ2+1.44g(1-g)ρ-4g·(1-g)C0=0

(25)

其中：

求解式(25)关于ρ的方程即可求得截面配筋率。

根据JTG 3362要求，纵向受拉钢筋的有效配筋率ρte，当ρte>0.1时，ρte=0.1；当ρte<0.01时，ρte=0.01。故应对上述计算所得的截面配筋率代入式(22)进行验证。若不满足要求，则可假定ρte=0.1或ρte=0.01，代入式(24)重新计算截面配筋率ρ，直到找到满足条件的截面配筋率。

3 算例

以某φ200 cm的圆柱形桥墩为例，墩柱计算长度为28.5 m，基本组合Nu=12 000 kN，Mu=9 000 kN·m;频遇组合Ns=10 000 kN,Ms=8 000 kN·m，计算该截面所需要的纵向主筋面积。墩柱采用C30混凝土，纵向主筋采用直径28 mm的HRB400钢筋，主筋中心到混凝土表面距离为9 cm，结构重要性系数γ0=1.0，最大裂缝宽度为0.15 mm。

裂缝宽度采用rho_()函数计算，求解方程6.114 726 8ρ3+0.978 356 3ρ2+0.117 936 0ρ-0.001 345 484=0，得ρ=0.010 445，配筋面积As=328.13 cm2，0.01<ρte=0.019 5<0.1，设计配筋采用54根直径28 mm的钢筋，配筋面积为332.51 cm2。按裂缝宽度计算公式对计算结果进行验算，钢筋应力σss=110.6 MPa，Wcr=0.148 mm<0.15 mm，满足要求。

4 结语

Python作为目前最受欢迎的编程语言之一，入门简单，功能强大。该文采用Python实现了一种解决圆形截面配筋的计算方法，能够按承载能力的相关公式计算截面的承载力及配筋，也可以按裂缝宽度验算的相关公式计算截面的配筋。采用Python语言实现的计算方法代码简洁易读，还可以结合图形实现算法优化，非常方便。