单向复合材料直梁的自由振动研究
黄 欣,郜浩然,郝 颖
(华北水利水电大学土木与交通学院,河南郑州 450045)
1 微分方程
采用高性能纤维增强复合材料部分代替传统金属材料,是建筑物和汽车实现轻量化有效途径。复合材料在变形过程中存在着拉伸—扭转、弯曲—扭转,以及不同面内变形之间的互相耦合。传统的 Euler-Bernoulli 梁理论和 Timoshenko 梁理论[1、2]基本上都延用平截面假定,忽略梁横截面的翘曲变形的影响。本文除了考虑空间轴线的曲率和扭率、经典的轴向、剪切变形和转动惯量的影响之外,另外计入扭转有关的翘曲变形的影响,推导得到单向复合材料矩形截面梁由14 个微分方程组成的运动微分方程来研究单向复合材料直梁的耦合振动。数值算例的结果证明方程的有效性,如图1 所示。

图1 矩形截面单向复合材料梁
设单向复合材料的柔度矩阵S 和刚度矩阵C=S-1,得到单向复合材料的应力应变关系。根据广义虎克定律和经典层合板理论可得 σ2=σ3=σ4=0,得到:

假定梁只发生伸长、扭转以及弯曲,则其位移场为:
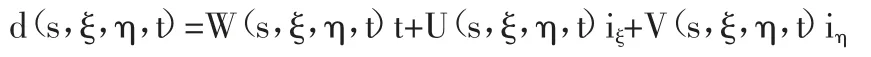
单向复合材料矩形截面杆自由扭转的圣维南扭转翘曲函数为:

假定梁在外力作用下,作频率为ω 的简谐振动。则梁的运动微分方程为:

矩阵中各元素如下所示。本文采用改进的Riccati 传递矩阵法求解固有频率。


表1 高宽比变化对梁固有频率的影响(L=1m)

表2 梁长变化对梁固有频率的影响

2 数值算例
两端固支的单向复合材料矩形截面直梁,E1=40E2,E2=E3=2Gpa,G12=G13=0.6E2,G23=0.5E2,μ=0.25,ρ=1500kg/m3,截面 2a×2b,梁长为L。
算例2.1:令L=1m,表1 展示了高宽比a/b 对梁固有频率的影响,如图2、图3 所示。

图2 不同高宽比对梁固有频率的影响
算例 2.2:令 2a=0.1m,2b=0.15m,表 2 展示了梁长 L 对梁固有频率的影响。

图3 不同梁长度对梁固有频率的影响
由表2 可知,随着梁长度的增大,梁的固有频率随之减小,翘曲效应的影响也随之增大。

