基于自适应虚拟惯量的孤岛VSG频率动态响应控制

李昱磊，赵巧娥

(山西大学 电力工程系，山西 太原 030013)

0 引 言

分布式电源通过电力电子变换器连接到电网以及向地区负荷供电[1]1，逆变器作为核心换流器件，其控制策略的设计对电力系统的稳定性和动态响应特性具有重要影响。

下垂控制逆变器缺乏充足的惯性和阻尼以支撑系统频率稳定[2]。因此，学者们提出了虚拟同步发电机(virtual synchronous generator，VSG)的概念[3]。VSG通过虚拟同步发电机的转动惯量和阻尼抑制受扰时功率和频率的波动。文献[4]建立了VSG的工频小信号模型，分析了控制参数对VSG性能的影响，给出控制参数的设计方法。但VSG受扰时，恒定虚拟惯量不能适应不同运行时段VSG对虚拟惯性的需求。为解决恒定虚拟惯量灵活性差的问题，学者们提出通过改变虚拟转动惯量来提高VSG动态响应性能。文献[5]提出一种自适应惯量的控制策略，根据VSG的角速度变化率和角速度偏差选取不同的虚拟转动惯量。文献[6]75提出一种不需要采样频率微分项的自适应虚拟惯性控制方法，但该控制算法实现时较为复杂。文献[7]提出一种协同控制虚拟惯量与阻尼的自适应控制策略，但阻尼系数与下垂控制相关一般设为固定值不宜改变。

为进一步提高VSG受扰时频率动态响应性能，本文提出一种基于角速度偏差以及角速度偏差与角速度变化率乘积的自适应虚拟惯量控制策略。在VSG不同运行时段内对虚拟惯量补偿不同的数值，从而抑制系统频率振荡并增强频率动态响应性能。通过MATLAB/Simulink对比另两种自适应虚拟惯量控制策略，验证了本文控制策略在VSG孤岛运行下的优越性。

1 VSG基本原理

孤岛模式下与负荷连接的VSG主要结构与控制如图1所示。

图1 VSG的拓扑图

图1中:Udc为逆变器直流侧等效电源;Lf和Cf分别为LC滤波器电感和电容；Ll和Rl分别为线路电感和阻抗；UPCC为公共连接点(point of common coupling，PCC)的电压；Iabc为输出电流；滤波电容电压Vabc为VSG输出电压。根据瞬时功率理论，计算P、Q输入到VSG控制。

VSG控制的有功频率和无功电压控制分别产生相角和电压幅值并合成调制正弦波，发送到脉宽调制模块产生逆变器的触发信号，控制框图如图2所示。

图2 VSG控制框图

有功控制与无功控制的方程如下：

(1)

式中：J为虚拟转动惯量；Pm为参考输入有功功率；Pe为电磁功率；D为阻尼系数；ω为角速度；ωn为稳态角速度；E为VSG内电动势；Eref为参考电压；K为调压系数；Qm为参考无功功率；Q为输出无功功率；Dq为无功功率调节系数。

2 VSG虚拟惯量自适应控制

2.1 虚拟惯量与系统稳定性关系

令Pm0=Pm-D(ω-ωn)，依据式(1)中有功频率控制方程得：

(2)

VSG输出功角δ的方程为：

(3)

依据式(2)、式(3)绘制功角特性曲线如图3所示。结合图4所示的孤岛VSG受扰后角速度振荡曲线仿真图，分析孤岛运行下VSG电磁功率和角速度的振荡机理。

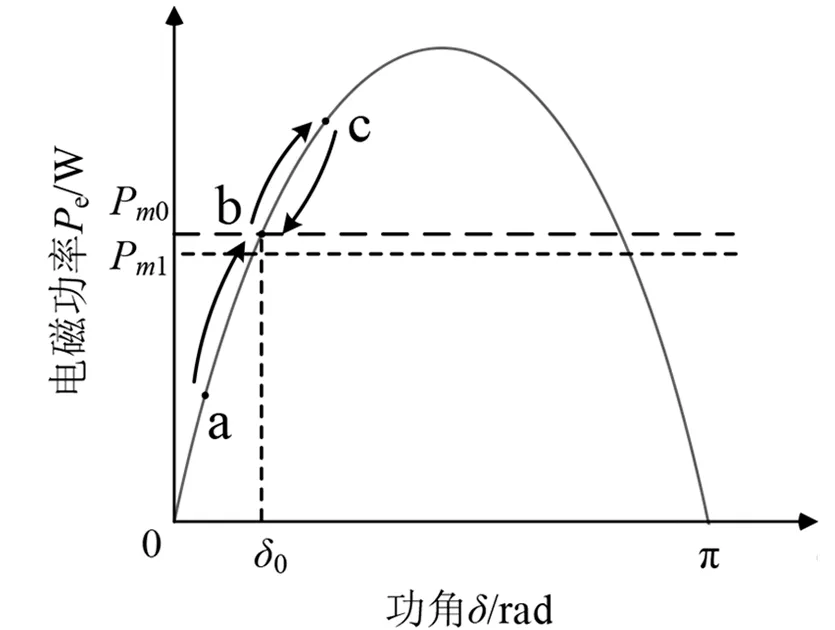
图3 VSG功角曲线

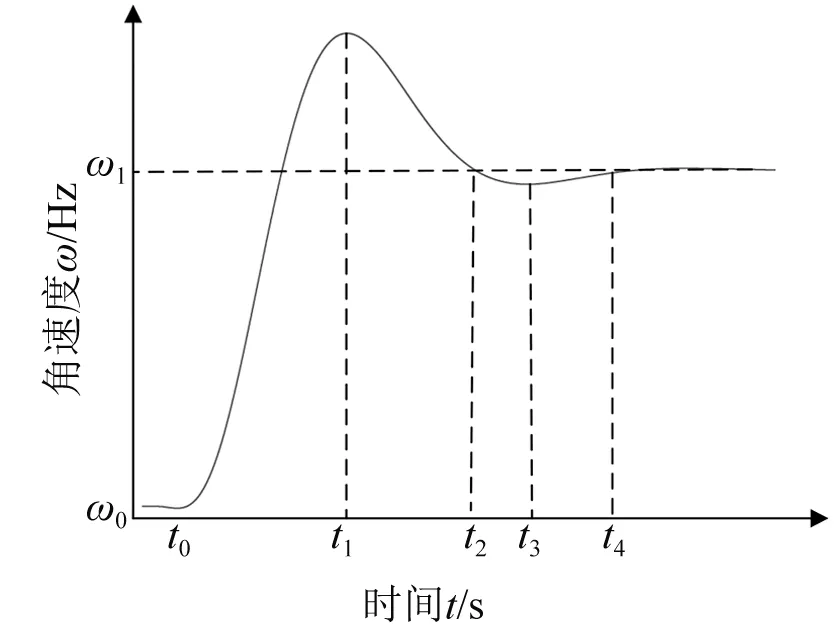
图4 角速度振荡曲线

t0时刻负荷减小，电磁功率Pe从平衡点b降低至a点，ΔP>0。由式(2)可知，角速度变化率增大dω/dt>0，系统角速度ω上升，如图4中t0～t1时间段所示。此时段内角速度偏差Δω=(ω-ω0)>0(ω0为受扰前的角速度稳态值)。随着电磁功率向b点移动，ΔP和dω/dt逐渐减小，ω上升到t1时刻Δω达到最大值。由式(3)可知,Pe运行到平衡点b时dδ/dt>0，Pe将越过b点向c点移动。

由b至c时段内，ΔP由正转负，即ΔP<0且偏差值逐渐增大，dω/dt与ΔP同号为负值。因此，ω由最大值逐渐减小直到运行至c点，如图4中t1～t2时间段所示。在Pe运行至c点时，Δω=(ω-ω1)=0(ω1为受扰后的角速度稳态值，由下垂控制决定)，但dω/dt<0，ω将减小，导致Δω<0。由式(3)可知，功角δ减小，使Pe减小向受扰后新的稳态平衡点(Pm1与功角特性曲线的交点)移动。t2～t3时段和t3～t4时段的分析与之类似。VSG受扰后角速度的偏差和变化率的动态过程如表1所示。

表1 角速度动态过程

由上述分析可知，VSG受负荷扰动后，在Δωdω/dt>0时，增大虚拟惯量可降低dω/dt值，具有抑制频率振荡的作用，但将增大调节时间。若下个负荷波动发生时角频率无法恢复稳定，角速度将在此基础上进一步波动，可能超出其要求的范围，严重时可造成功角失稳。当Δωdω/dt<0时，减小虚拟惯量可降低调节时间，却会增大角速度的峰值。

2.2 自适应虚拟惯量的控制策略

为平衡频率的响应快速性与抑制振荡之间的矛盾，本文提出一种以Δω和Δωdω/dt作为虚拟惯量补偿值的自适应控制策略。虚拟惯量取值原则为：

(4)

式中：J0为虚拟惯量稳态值；ka和kb为相应补偿项的补偿系数；C为判定阈值。目的是避免VSG处于稳态运行时，由于角速度偏差值或角速度变化率出现细微偏差而引起自适应虚拟惯量控制的误动导致虚拟惯量的变化，保证VSG稳态时的稳定性。

式(4)对虚拟惯量的调节有如下特点：

(1)角速度偏离稳态值时(如图4中t0～t1时间段)，对J0补偿ka|ω-ωn|。由于角速度变化初期ω-ωn的值较小，J0的补偿量较小，有利于角速度迅速向新的稳态值过渡以提高快速响应性能。当角速度临近稳态值时ω-ωn较大，使J大幅增加，有利于抑制频率振荡。

(2)角速度向稳态值恢复时(如图4中t1～t2时间段)，通过减小J0的值使角速度快速向稳态值恢复；当角速度靠近新的稳态值时Δω较小，使J0的减小量Δωdω/dt很小，避免由于虚拟惯量的减小使角速度变化率较大影响VSG稳定性。

因此引入式(4)，可提高VSG响应的快速性，同时增强抑制频率振荡的性能。

2.3 参数整定

1)阻尼系数D

设定VSG角速度限制范围为[ωmin，ωmax]，为使VSG稳定运行阻尼系数取值应满足式(5)。

(5)

式中：Pmax和Pmin为VSG允许输出有功功率的最大值和最小值。

2)虚拟惯量稳态值J0

VSG控制设计为二阶系统，阻尼比ζ为：

(6)

为便于参数的整定认为功角的初值δ0≈0°，cosδ0≈1，取ζ∈[0.1～0.8]，得稳态虚拟惯量J0的取值范围为：

(7)

3)补偿系数ka

根据式(4)，角速度偏离稳态值时补偿系数ka满足：

(8)

VSG受扰过渡到稳态的角速度偏差为：

Δω=-ΔP·D

(9)

将式(8)代入式(9)得ka的表达式为：

(10)

参见文献[1]3设计的VSG方案虚拟惯量J的取值为：

(11)

结合式(7)、式(10)和式(11)可依据实际情况综合整定ka的取值。

4)补偿系数kb

角速度向稳态恢复时kb可参见文献[6]79取值：

(12)

式中：ΔPmax为有功功率允许偏差的最大值。

实际工程设计中，补偿系数ka和kb的取值还需要参考直流侧储能装置的容量以及响应特性等方面综合设定。

3 仿真分析

通过MATLAB/Simulink搭建图1所示的单台VSG仿真模型。在VSG孤岛运行模式下对文献[6]76和文献[8]提出的自适应虚拟惯量控制策略进行对比，验证本文所提控制策略的优越性。仿真主要参数如表2所示。负荷变化后频率波动的仿真结果如图5所示。

表2 仿真参数

0 s时VSG启动，初始负荷有功功率10 kW，无功功率5 kvar；0.1 s时切除有功功率2 kW，无功功率2 kvar的负荷；0.2 s时新增有功功率10 kW，无功功率5 kvar的负荷。三种自适应虚拟惯量控制策略的对比仿真如图5所示。

图5(a)为分别采用三种自适应虚拟惯量控制的VSG投切负荷时的频率波动图。图5(b)为切负荷后频率偏离初始稳态值的横纵坐标放大波形图[图5(a)中0.11～0.12 s]。图中实线表示自适应虚拟惯量控制策略相比于其他两种控制策略可降低系统频率波动的峰值，即可减小超调量防止频率超出允许的变化范围。表明本文设计的控制策略具有优于另两种控制策略的抑制频率振荡的性能，从而进一步提高了系统稳定性。

图5 负荷变化时VSG仿真波形图

图5(c)为除负荷后频率稳定至新稳态值的横纵坐标放大波形图[图5(a)中0.12～0.13 s]。如图5(c)所示，本文的控制方法在频率恢复阶段的波形曲线始终位于另两种曲线之下，表明本文所提的自适应虚拟惯量控制策略可进一步降低受扰后VSG的调节时间，增强了VSG频率快速响应性能。

图5(d)为0.2 s增负荷后频率跌至最小值的横纵坐标放大波形图。由图可知，采用本文的控制策略在负荷增加时可更有效地抑制频率振荡幅值，提高了频率的动态响应性能和稳定性。可见，本文的控制策略更有效地降低VSG受扰后频率振荡幅值和调节时间。

4 结束语

本文对VSG受扰后频率响应进行研究，设计了一种基于角速度偏差和角速度偏差与角速度变化率乘积为虚拟惯量补偿量的自适应控制策略。该策略具有动态平衡频率响应快速性与抑制频率振荡的作用。通过MATLAB/Simulink对孤岛VSG进行仿真，在不同负荷波动的情况下对比另两种自适应虚拟惯量控制，验证了本文控制方法可更有效抑制频率振荡，减少超调量，同时降低频率响应的调节时间。