梯级变幅交变荷载下伤损RC梁静动力性能全过程演化

费忠宇，王少杰，苗嘉伟，石若汐，张坤强

(1.山东农业大学 水利土木工程学院，山东 泰安 271018；2.北京交通大学 土木建筑工程学院，北京 100044)

客货共线铁路旧桥在中国铁路桥梁中占比巨大，普通钢筋混凝土(RC)梁桥早期得到普遍应用，且其中绝大部分已步入生命周期中老年阶段[1]。回顾中国铁路发展历程[2-3]可知，在1997年首次提速前，客货共线列车运速较低、运力较弱，铁路旧桥在此状况下承受的应力值较低；至2007年左右，我国铁路完成了六次大提速，列车运速与运力得到提高，桥梁承受的应力值增大；之后，高速铁路、动车的快速发展释放了铁路客运压力，使得货运列车增多，铁路旧桥在交变荷载作用下承受的应力值再次提高。综上可知，中国客货共线铁路桥承受的载荷实际上呈现梯级变幅增长特点，而梁的疲劳寿命又与承受的应力幅三次方成反比例关系[4]，且RC梁桥允许带缝工作[5]，因此以客货共线铁路实际服役历程为背景对伤损RC梁开展梯级变幅交变荷载下的全过程性能演化研究，对铁路旧桥的长期安全稳定服役具有重要意义[6]。

围绕RC梁在疲劳荷载作用下的静动力性能演化，国内外研究主要集中在等幅疲劳[7-13]。然而，实际中仅仅承受等幅疲劳荷载的状况较少[14]，中国客货共线铁路旧桥实际承受的是梯级变幅交变荷载，故必须采用与实际情况相吻合的变幅疲劳试验。相较于等幅疲劳，有关变幅疲劳的研究多数集中在两级变幅或随机变幅且相对较少。其中，冯秀峰等[15]通过研究表明，随机变幅疲劳寿命要远低于以等幅疲劳为加载制度获得的疲劳寿命，因此以等幅试验结果去衡量构件的疲劳寿命十分危险；雷俊卿等[16]针对2片后张法PC梁，分别开展了二级与多级变幅疲劳加载试验，基本结论是PC梁在变幅疲劳荷载下的疲劳累积损伤更为严重；Keerthana等[17]对混凝土材料开展了4级变幅疲劳试验研究并进行理论分析。然而关于伤损RC梁在梯级变幅交变荷载作用下的试验研究相对匮乏。

本文以铁路旧桥为背景，采取双作动器同步疲劳方式对伤损RC梁进行梯级变幅交变加载，研究伤损RC梁在不同疲劳状态下对应的静力性能、受迫动力响应及自振特性全过程演化规律，旨在深入认知考虑低应力加载历程时伤损RC梁体的服役性能，能为RC铁路旧桥科学管养提供成果支持。

1 试验概况

1.1 试件设计

试验梁的尺寸及配筋图见图1，采用三分点加载，相同规格的试件共设计制作2根，其中B1梁进行静力加载、B2梁进行梯级变幅交变荷载下的疲劳加载。试验梁截面尺寸为150 mm×300 mm(宽×高)梁长3.3 m、支座间距3.0 m。试验梁为钢筋混凝土梁，混凝土强度实测等级为C30，保护层为25 mm；上下侧的架立筋与纵筋直径分别为14、18 mm，钢筋等级为HRB400；箍筋直径为8 mm，钢筋等级为HPB300，加密区与非加密区间距分别为100、150 mm。

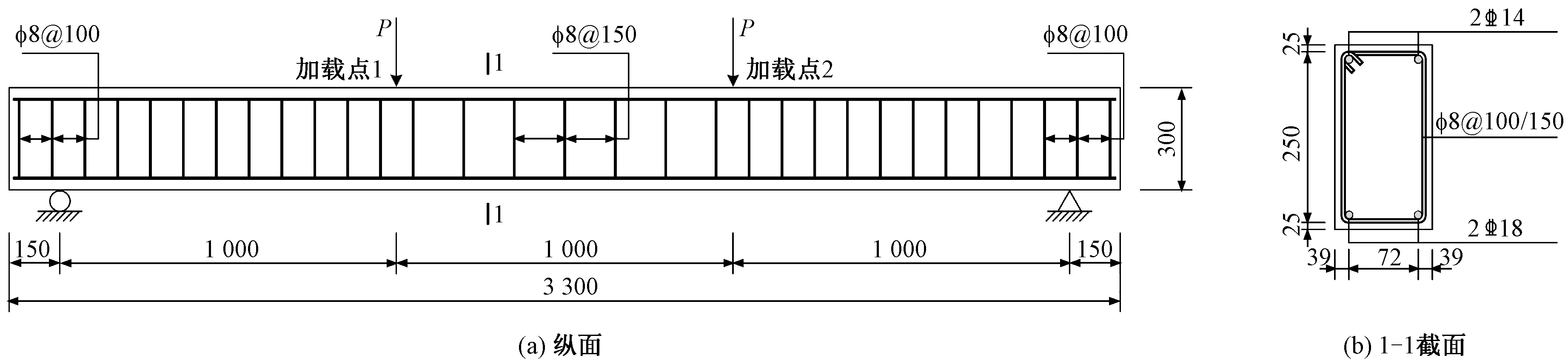
图1 试验梁尺寸及配筋(单位：mm)

1.2 静力加载

依据GB/T 50152—2012《混凝土结构试验方法标准》[18]对B1梁进行静力加载至破坏，荷载-变形曲线见图2，对应弯矩实测极限承载力Mu为40.53 kN·m。梁失效破坏后对应裂缝分布见图3(方格尺寸为50 mm×50 mm)，静载全过程共产生21条裂缝，有5条宽度超过1.5 mm的主裂缝，其中位于跨中的裂缝最宽达4.25 mm并延伸至受压纵筋，裂缝主要对称分布在梁体纯弯段。

图2 B1梁弯矩-变形曲线

1.3 疲劳加载1.3.1 加载制度

实际桥梁因大部分带裂缝服役而表现出一定的损伤状态，B2梁则以此为背景，在梯级变幅交变加载前，先将梁体静力致裂，在确定开裂荷载后转入疲劳(加载频率为2.0 Hz)，加载制度见图4，以货运列车应力水平Si为上限，以客运列车应力水平0.76Si为次上限，下限定为0.10Mu，整体呈梯级变幅与客货交变特点。具体而言：前100万次疲劳为低应力水平(0.31Mu)，模拟裂缝的“呼吸”特征；100万～200万次为较低应力水平(0.34Mu)，较前阶段增大约10%用来模拟列车提速；200万次后，为加速试件损伤累积使其最终发生疲劳破坏，将中、较高、高应力水平分别设定为0.55Mu、0.65Mu、0.75Mu。五级变幅交变加载能充分反映实际客货铁路旧桥的长期服役特点，并为同类桥体在服役周期内的疲劳性能评估提供有益探索。

图3 B1梁裂缝分布(单位：mm)

图4 疲劳加载制度

1.3.2 加载装置

采用MTS液压伺服控制系统加载。

梁的两端分别使用滚轴支座、固定铰支座来支承梁体，加载时通过竖向反力架提供反力；为保证两加载点所受荷载相一致，未采用“单一作动器+分配梁”方案，而是在两三分点处分别采用1个最大量程500 kN、变形±250 mm的作动器并由同一MTS系统控制。后续试验证明了上述MTS双作动器同步加载技术与装置满足试验要求，且能长期稳定运行。

1.4 测点布置与数据采集

针对静力与疲劳试验，主要测试变形、应变等静动力响应，其测点布置详见图5。共5个变形测点(D1—D5)分别布置在跨中、支座、四分点处；14个钢筋应变测点(L/RS1—L/RS7)分别布置于下侧纵筋；14个混凝土应变测点(L/RC1—L/RC7)沿梁体高度方向在跨中两侧分别布置。静力采集时，各项数据的采样频率为2.0 Hz；疲劳采集时，为提升精确度将采样频率提升至1 024 Hz；疲劳过程中对各项数据进行实时监测并在每一次停机后统计残余变形。

图5 测点布置方案(单位：mm)

结构自振特性是结构自身固有属性，可从一定程度反映其损伤状态[19]。为了揭示不同疲劳次数下伤损RC梁体的自振特性全过程演化规律，在达到预定循环加载次数并停机后，测试试验梁B2的横向与竖向前6阶振型、自振频率与阻尼比等自振特性，测试过程中梁体竖向、横向采样频率分别定为5 012、2 560 Hz。依据上述方法，能够通过测试得到试验梁竖向、横向各阶自振特性。

2 试验现象

2.1 裂缝演化

梯级变幅交变荷载下试验梁B2在各应力水平加载结束后对应的裂缝发展情况详见图6。开裂伤损状态对应的裂缝分布见图6(a)，首条裂缝对应开裂荷载为9.50 kN·m，首批两裂缝宽度均为0.10 mm、长5 cm，之后停止静力加载，转入疲劳加载。首级疲劳加载(开裂～100万次)对应低应力水平，裂缝于前30万次集中产生(总共11条)，后70万次仅产生1条裂缝，表现为先迅速后稳定的发展状态(见图6(b))。至第2级疲劳加载(100万～200万次)，相应应力水平较首级提升10%，全过程仅出现3条新裂缝(见图6(c))，且均在应力水平提升初期(100万～115万次)。第3级疲劳加载(200万～300万次)的荷载峰值对应0.55Mu，该阶段前25万次有5条新裂缝产生，而后75万次仅在北侧加载点处新出现2条细微裂缝，本级加载约以225万次疲劳为分界点，裂缝在其之前迅速演化，而后步入稳定阶段(见图6(d))。第4、5级疲劳加载全程仅出现2条短裂缝，裂缝整体数量已趋于平稳(见图6(e))，主要表现为旧裂缝在原有基础上的不断扩展；至4 268 798次时梁体于跨中偏北约10.50 cm处突然产生疲劳断裂，缝高瞬间发展至架力筋处(见图6(f))。试验梁B2破拆证实梁体下部有1根纵筋发生脆性断裂，断口有明显颈缩现象、断裂面较为平直。

图6 各级应力水平加载结束后对应的裂缝分布(单位：mm)

综上可知，梁体裂缝在梯级变幅交变荷载作用下表现出以下规律：大部分裂缝在每级应力水平提升的初期出现并快速演化；针对试验全过程，裂缝出现在加载初期较多后期较少(约以275万次为界)，且分布趋势从纯弯段向加载点移动；以跨中截面为中心，裂缝均匀对称分布；疲劳断裂时，断裂处裂缝大幅扩展，其余裂缝迅速闭合。

2.2 残余变形

试验梁B2对应的累积残余变形-疲劳次数关系曲线详见图7。由图7可知：伴随疲劳加载次数增加，累计残余变形不断增加；在每次应力水平提升初期，对应的残余变形增速较大；高应力水平作用下对应的累积残余变形显著大于低应力水平，至梁体疲劳破坏时对应的累积残余变形为1.33 mm，对应挠跨比约为1/2 256。

图7 累积残余变形-疲劳次数关系曲线

3 结果分析

3.1 伤损RC梁静力性能全过程演化

3.1.1 应变

梯级变幅交变荷载反复作用后，试验梁在同等静荷载下的应变存在演化。以跨中测点LS4、LC6为例，绘制不同疲劳次数加载后梁体静力荷载-应变关系曲线，见图8。由图8(a)可知，疲劳加载全过程对应的纵筋应变先增后降再增加，即疲劳10万次后相同荷载对应的应变较开裂增大、疲劳55万次后相同荷载对应的应变较10万次降低、至疲劳加载100万次相同荷载对应的应变才再次增长至大致与10万次对应的应变相当但仍略小、之后伴随疲劳次数增加纵筋应变渐次增大，加载至325万次应变片失效前规律未变；疲劳加载之初，纵筋应变伴随疲劳次数增加反而呈下降特点，是因为纵筋与混凝土之间产生黏结滑移致使钢筋回缩、应变降低，且应变降低量大于低应力水平下伴随疲劳次数增加致钢筋应变的增加量，在应力水平提高后，纵筋应变伴随疲劳次数的增加而增长。图8(b)反应了疲劳过程中混凝土应变与纵筋应变演化规律的不同，具体表现为相同静载下混凝土应变随着疲劳单调增加，至400万次疲劳后最大静载下混凝土应变达289.8×10-6；另外，高应力水平下的混凝土应变增速要显著大于低应力水平。

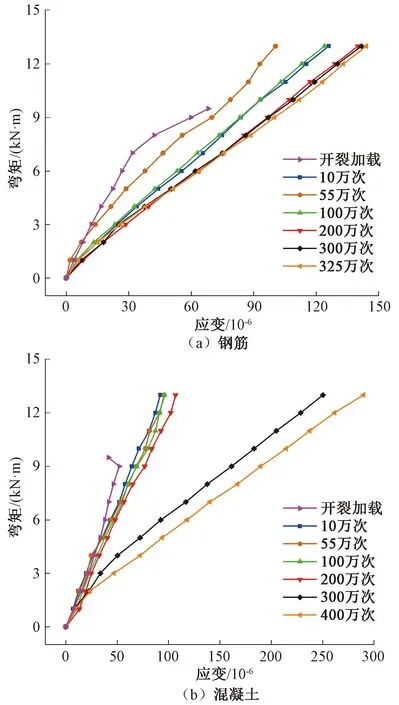
图8 不同疲劳次数后梁体静力荷载-应变关系曲线

3.1.2 变形

静力荷载下梁的变形性能直接表征其抗弯刚度，以试验梁B2对应的跨中变形测点D3为例，据实测数据绘制其在不同疲劳次数后梁体静力荷载-变形关系曲线，见图9(a)；经过线性拟合[20]，得到抗弯刚度退化曲线，见图9(b)。由图9可知，伴随疲劳次数、应力水平的增加，梁体抗弯刚度出现明显退化，体现为梁体静刚度在疲劳加载全过程的伤损退化。进一步分析：疲劳初期(开裂～10万次)，梁体抗弯刚度从7.82 kN/mm下降至6.24 kN/mm，降幅达20.20%；至疲劳100万次，应力水平没有变化，梁体抗弯刚度微幅降低，即低应力水平下梁体抗弯刚度的降低主要集中在疲劳加载初期阶段；100万～400万次疲劳加载阶段，梁体的抗弯刚度近似呈线性降低趋势，平均降速达到每百万次0.61 kN/mm，疲劳加载至400万次时梁体对应的抗弯刚度约是开裂加载状态的58.31%。

图9 不同疲劳次数后梁体变形与刚度退化

3.2 梯级变幅交变荷载下伤损RC梁动力性能全过程演化

3.2.1 应变

与静力荷载作用下的受力性能相比，梁体在梯

级变幅交变荷载下产生应变演化的同时存在动力放大效应。为便于对比，取与3.1.1节相同的应变测点LS4、LC6，绘制其不同疲劳加载次数后梁在低应力水平(0.31Mu)交变荷载作用下的应变-时程关系曲线，见图10。

图10 不同疲劳次数后梁体在低应力水平交变荷载下的应变-时程曲线

由图10(a)可知，与静力荷载作用下的应变演化类似，因纵筋与混凝土之间黏结滑移，致使纵筋回缩其应变亦呈“先增后降再增加”的演化特点；由图10(b)可知，相同疲劳荷载作用下梁体混凝土应变随疲劳次数增加而单调增加，整体以200万次为界，演化速度在低、较低应力水平下较慢，应力水平提高后明显增加。取同阶段梁体动、静力应变比值表征应变动力放大效应，以低应力水平对应荷载12.56 kN·m为例，在经历100、200、300、400万次疲劳加载后，纵筋在动力荷载作用下的应变幅值分别是153.5×10-6、160.8×10-6、164.6×10-6、172.2×10-6，静荷载作用下的应变分别是124.0×10-6、140.0×10-6、141.8×10-6、144.0×10-6，即对应的动力放大系数分别为1.24、1.15、1.16、1.20；与纵筋相对应，梁体混凝土应变在动力荷载下的幅值分别是109.8×10-6、117.1×10-6、276.1×10-6、316.0×10-6，静荷载作用下分别是96.3×10-6、106.8×10-6、250.4×10-6、289.8×10-6，即对应的动力放大系数分别为1.14、1.10、1.10、1.09。

3.2.2 变形

(1)跨中位置

不同疲劳次数后梁体在低应力水平交变荷载作用下跨中变形-时程关系曲线及峰值变形演化曲线，见图11，由图11可知，伴随疲劳次数、应力水平的增加，梁体在同等动力荷载作用下跨中变形逐渐增大，动刚度逐步下降；就变形增速而言，低应力水平明显小于高应力水平，即应力水平大小会对梁体刚度及疲劳寿命产生直接影响。低应力水平的应力上限、次上限荷载对应的跨中峰值变形-疲劳次数关系曲线见图11(b)。由图11(b)可知，两条曲线近乎平行，在各级应力水平提升之初梁的变形会有突增，次上限荷载下的跨中峰值变形约是上限荷载的0.75倍，与次上限荷载所占上限荷载的比例系数0.76近乎相等。对动力放大效应的分析以上限荷载为例，在经历100万、200万、300万、400万次疲劳加载后，动力荷载作用下梁体跨中对应的峰值变形分别是2.01、2.16、2.47、2.73 mm；与之相对应，经历相同疲劳次数后跨中对应的静力变形分别是1.95、2.12、2.45、2.65 mm，即对应动力放大系数分别是1.03、1.02、1.01、1.03，由此可知跨中变形存在动力放大效应但不明显。

图12 各级应力水平下加载点处对应的荷载-变形曲线

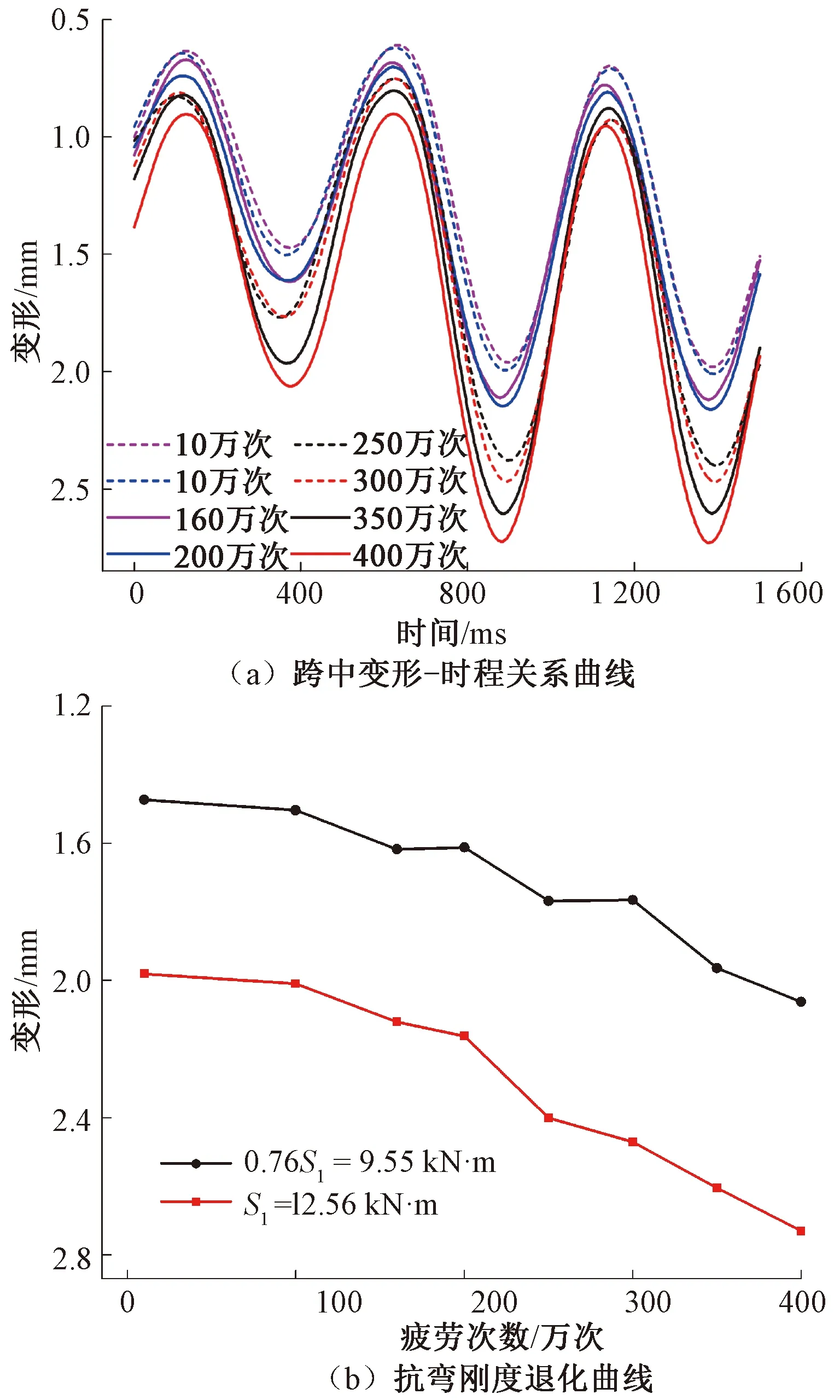
图11 不同疲劳次数后低应力水平交变荷载作用下梁体跨中变形的演化

(2)加载点处

如1.3.2节所述，在进行试验加载时直接在三分点处分别采用MTS作动器施加，故可以分别得到梁体在两个加载点处的荷载-变形曲线。各应力水平下(S1～S4)特定疲劳次数(0、100万、200万、300万、400万次)对应的荷载-变形曲线，见图12。图中的实线对应加载点1，虚线对应加载点2。由图12可知，随着疲劳次数增加，各级荷载-变形曲线均呈现向右移动的趋势，表明梁体刚度在逐渐退化，且高应力水平对应的退化程度明显大于低应力水平；应力水平与疲劳次数均相同时，两个加载点处对应曲线存在差异，可归因于加载点处局部损伤的随机差异性发展；伴随疲劳次数的增加尤其是应力水平的提高，曲线所包围的面积逐渐增加，体现为梁体耗散的能量在增加，内部损伤在累积演化。在高应力水平S5作用下，试验梁B2在加载至4 268 798次时突然疲劳断裂，梁体断裂及之前50次疲劳加载对应的荷载-变形曲线见图13。由图13可知，在疲劳断裂前的极短时间里，梁体快速变形，最终的疲劳破坏体现为典型的脆性断裂。破拆梁体断裂处发现，有1根纵筋发生脆性断裂、另1根纵筋表观完好。

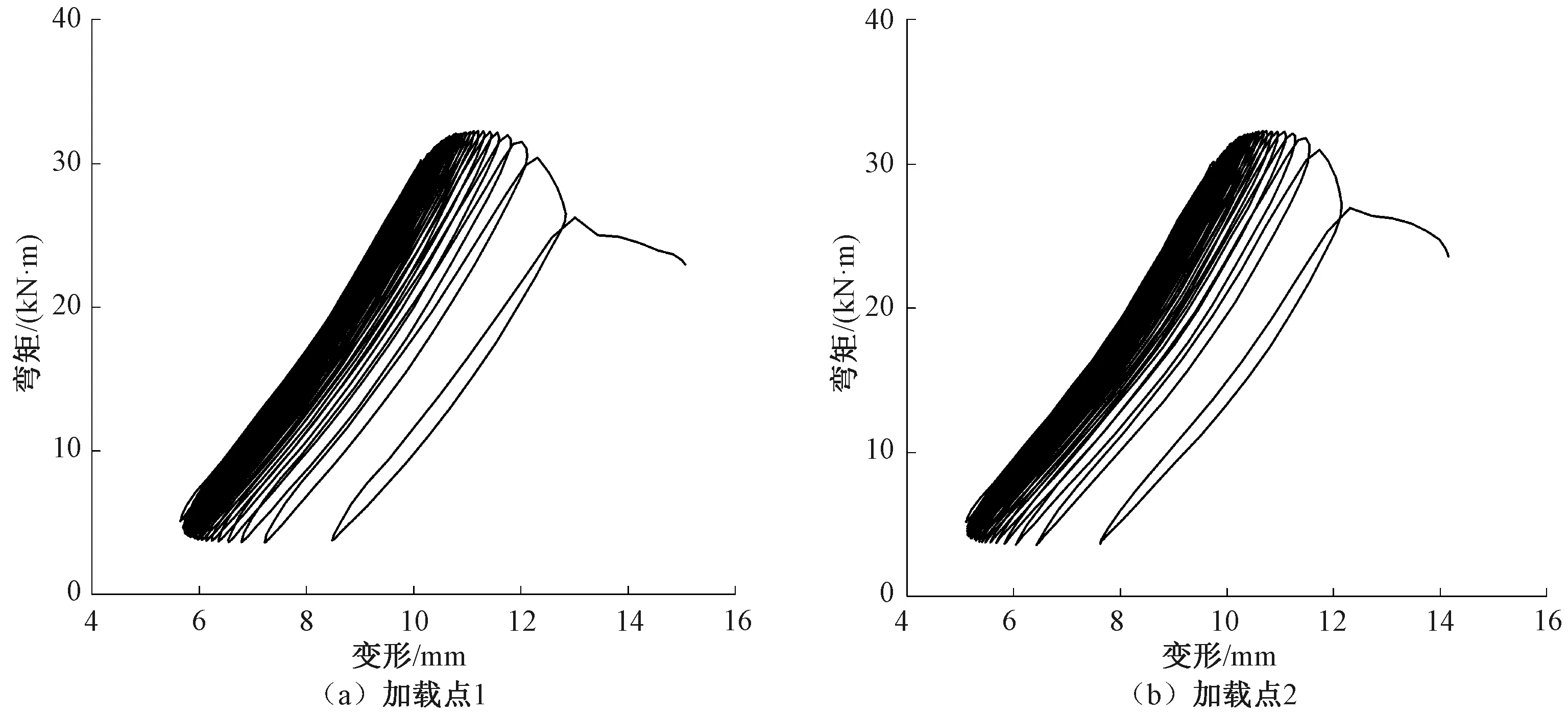
图13 疲劳破坏前加载点处的荷载-变形曲线

3.3 伤损RC梁自振特性全过程演化

3.3.1 振型

以B2梁疲劳加载至300万次为例，其竖向前6阶实测弯曲振型见图14；MAC(模态显信准则)验证见表1，表明测试准确可靠。基于验证后的梁体振型，可通过自振特性测试辅助精准确定梁体在不同时刻对应的各阶自振频率、阻尼比，最终用于评价RC梁的伤损演化状态。

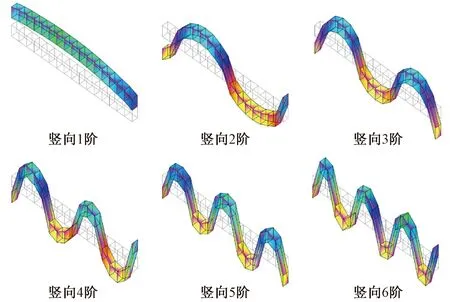
图14 疲劳加载300万次后试验梁B2对应的模态测试结果

表1 MAC验证

3.3.2 自振频率

试验梁B2的模态测试在实验室内完成，能最大程度保证测试环境的稳定性，梁体各阶自振频率统计详见图15。由图15可知：随着疲劳加载次数的不断增加，梁的横、竖向不同阶自振频率均有所下降，且高阶下降幅度大于低阶；同完好状态相比较，裂缝是梁自振频率产生下降的最主要原因；疲劳至100万次时对应的自振频率延续了上述下降特征；200万～400万次期间，梁体横、竖向各阶自振频率亦有下降，但下降幅度明显收窄；疲劳断裂后，梁体各阶自振频率下降程度更为明显，其中B2梁断裂后的第6阶横、竖向自振频率较400万次疲劳加载后分别下降85、278.125 Hz，自振频率的巨幅变化为判断梁体筋材是否发生疲劳断裂提供了简便方法(前述已知未发生疲劳断裂前梁体自振频率变化较小)，尤其适用于钢绞线成束布置的工况，即部分钢绞线失效时可以通过测试梁体自振频率予以充分表征。

图15 梁体疲劳全过程前6阶弯曲振型对应的自振频率变化

3.3.3 阻尼比

统计分析各加载阶段梁体的横、竖向不同阶阻尼比发现仅有前1阶存在变化规律，见图16。

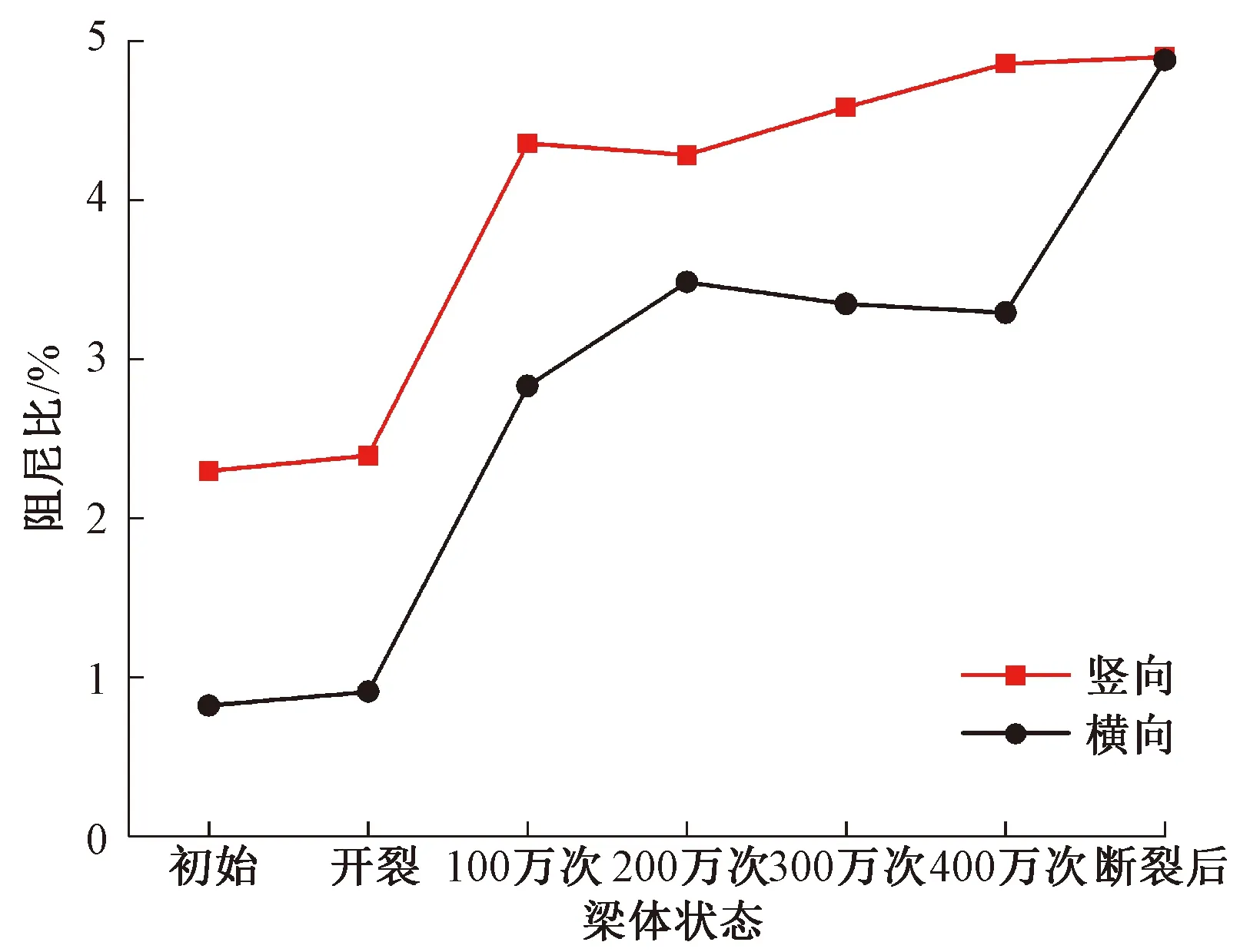
图16 梁体疲劳全过程1阶竖向、横向阻尼比变化曲线

由图16可知，疲劳加载过程中梁的横、竖向阻尼比均呈增大趋势，初始状态至疲劳400万次时梁的横、竖向阻尼比分别由0.82%、2.29%各自增至3.29%、4.85%，增幅较为明显；断裂前，梁体竖向阻尼比大于横向；断裂后梁体横、竖向阻尼比分别为4.88%、4.90%，二者近乎相等。

4 结论

(1)梯级变幅交变荷载作用下，裂缝、残余变形多集中在各级应力水平提升之初扩展或累积；纵观试验全过程，裂缝出现集中在加载初期、中期，至后期多是先期裂缝的变宽、变长；伴随疲劳次数的增加累积残余变形不断增加，后期高应力水平对应的残余变形明显大于低应力水平；试验梁加载至4 268 798次时突然在跨中断裂，纵筋断口有明显颈缩、断面较为平直。

(2)加载全过程，纵筋应变呈先增后降再增加的演化特点，即在低应力水平下，纵筋与混凝土之间黏结滑移致钢筋回缩、应变降低，且降低量大于疲劳伤损所致应变的增加量；混凝土应变随疲劳次数增加而单调增加，高应力水平下的增速明显大于低应力水平。

(3)随着疲劳次数、应力水平的不断增加，梁的抗弯刚度存在明显退化，梁体耗能增多，整体呈三阶段特征，即加载初期虽应力水平较低，但裂缝萌生、发展迅速，至疲劳加载10万次时刚度降幅已达20.20%；之后，近似呈线性趋势降低，平均降速约为每百万次0.61 kN/mm；至疲劳断裂前，梁的变形明显增加，刚度再次快速下降。

(4)梁体在梯级变幅交变荷载作用下，应变、变形均存在动力放大效应；以跨中测点为例，纵筋应变、混凝土应变、梁体变形对应的动力放大系数平均值分别是1.188、1.108、1.023，即同种应力水平下，纵筋所承受的动力放大效应最大。

(5)随着疲劳次数和应力水平的不断增加，梁的横、竖各阶自振频率均出现不同幅度下降(高阶大于低阶)，第1阶阻尼比均呈增大趋势；单根纵筋疲劳断裂后，梁的横、竖向各阶自振频率均明显下降，这为建立基于自振频率的筋材失效断裂评估方法提供了潜在路径。