基于粒子群算法与RBF 神经网络的露天矿边坡稳定系数预测

韩 亮，贺昌斌，柴书罡

（中煤平朔集团有限公司 安太堡露天矿，山西 朔州 036006）

现有边坡稳定性分析的确定性方法理论完善，推导严谨，在工程实践中具有一定的实用性及可靠性；然而，露天矿边坡是一个动态、开放的复杂系统，其稳定性不但受地质、工程等各种可测的确定性因素影响，还受多种随机、模糊、可变、不可测的不确定性因素影响，各种影响因素之间的关系复杂，且往往是非线性的，导致边坡稳定性分析评价很难或不可能建立明确的数学、力学模型并进行准确地求解；此外，由于确定性方法在进行边坡稳定性分析评价时，仅选择了其中起主要控制作用的可测因素建立模型，对不可测因素进行了简化，导致了评价结果存在一定程度的不可靠性[1]。

RBF 神经网络预测精度很大程度上依赖于网络的隐含层基函数中心值C、宽度σ 以及隐含层至输出层的连接权值w 等参数的选择，RBF 神经网络参数主要通过经验与试算的方式确定，极易由于参数选取不当对RBF 神经网络的收敛性及预测精度产生较大影响。为克服RBF 神经网络参数选取不当产生的问题，引入具有全局搜索能力的粒子群算法（Particle Swarm Optimization，PSO）对RBF 神经网络参数进行优化，在此基础上，构建RBF 神经网络预测露天矿边坡稳定系数。

1 粒子群算法与RBF 神经网络

1.1 粒子群算法

粒子群算法（Particle Swarm Optimization，PSO）是Kennedy 与Eberhart 于1995 年提出的群体智能仿生优化算法，算法采用“群体”与“进化”的概念，群体由在n 维搜索空间中的个体（粒子）构成，个体在搜索空间以一定速度飞行，飞行速度由个体的飞行经验和群体的飞行经验进行动态调整，并依据个体的适应值大小决定下一步操作。

粒子群算法初始时刻，将数据进行聚类后得到的聚类中心设置为第一批潜在解，并随机生成第一批速度向量Vi，在每一次迭代中，粒子通过跟踪个体极值Pbest和全局极值Gbest更新自己的位置与速度[2]：

式中：k 为当前迭代次数；V 为粒子速度；X 为粒子位置；c1、c2为加速因子，为非负常数；r1、r2为分布于[0，1]之间的随机数。

1.2 RBF 神经网络

RBF（Radial Basis Function，径向基函数）神经网络由于具有结构自适应确定、系统输出与初始权值无关等优良特性，在多维曲面拟合、自由曲面重构等领域得到广泛应用[3]。

基本RBF 神经网络由3 层构成，第1 层是输入层，其作用是连接网络与外界环境，将信号传递到隐层；第2 层为唯一的一个隐层，其作用是从输入层到隐层之间进行非线性变换，与BP 神经网络不同，大多数情况下隐层都具有较高的维数，其神经元传递函数由呈辐射状的作用函数-径向基函数构成；第3层是线性输出层，它对作用于输入层的激活模式做出响应。

RBF 神经网络常用的基函数有以下几种形式[4]：①高斯函数；②复二次函数；③广义复二次函数；④逆复二次函数。最常用的是高斯核函数：

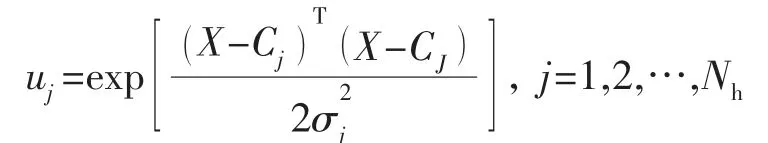
式中：uj为第j 个隐层节点的输出；X 为输入样本；Cj为高斯函数的中心值；σj为标准化常数；Nh为隐层节点数。

由上式可知，节点输出范围在0～1，且输入样本越靠近节点中心，输出值越大。

相关研究表明[5]，RBF 神经网络与BP 神经网络一样具有以任意精度逼近任意连续函数的能力，两者的主要差别在于各自使用了不同的作用函数。BP神经网络隐节点作用函数的函数值在无限大的输入空间范围内为非零值，而RBF 神经网络中的径向基函数作用则是局部的。由于RBF 神经网络的隐层径向基函数族是闭集，可以达到与被逼近函数距离范数的下确界，是最佳逼近，而BP 神经网络隐层作用函数的逼近函数族是非闭集合，所以不具有最佳逼近性质。因此，RBF 神经网络具有BP 神经网络无法比拟的优点：全局优化、最佳逼近的性质，以及相对快速的学习方法[6]。

2 基于粒子群与RBF 的边坡稳定系数预测模型

2.1 露天矿边坡稳定系数的原理

基于粒子群算法与RBF 神经网络预测边坡稳定系数的实质是曲面插值，认为影响边坡稳定性的定量化因素与稳定系数的空间分布能够用一个复杂的非线性函数进行逼近，建立边坡稳定性影响因素与稳定系数之间的函数关系：

式中：x1,x2,…,x 为影响边坡稳定的定量化因素；fs为边坡稳定系数。

RBF 神经网络以边坡岩体密度ρ、黏聚力C、内摩擦角φ、边坡角α、边坡高度H、孔隙压力比γu等6 个可量化的影响因素作为网络输入，以边坡稳定系数fs作为网络的输出，即网络的输入层节点数为6，输出层节点数为1。用已获得的量化的边坡稳定性影响因素及稳定系数为训练样本对RBF 神经网络进行训练，将边坡稳定性影响因素属性值与边坡稳定系数之间的非线性函数关系隐藏在收敛后的RBF 网络之中，然后将待预测的边坡影响因素量化属性值作为网络输入，利用训练好的RBF 神经网络进行仿真预测，即可得到待预测边坡的稳定系数。

预测边坡稳定系数的RBF 神经网络拓扑结构如图1。

图1 边坡稳定系数预测RBF 神经网络拓扑结构

粒子群算法模拟的蚁群搜索方式克服了传统算法依赖初始聚类中心且容易陷入局部最优的缺点。粒子群算法以RBF 输入数据拟合残差绝对值的和为适应度值，并将粒子群算法作为RBF 神经网络训练的前导性计算，以期获得RBF 神经网络训练的最优参数值。

粒子群算法的目标函数min f（i）为：

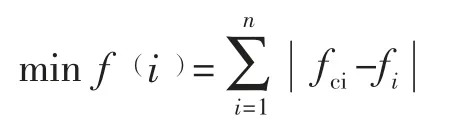
式中：fci为通过模型计算得到的边坡稳定系数值；fi为已知样本点边坡稳定系数值；i 为样本数据序号；n 为样本数据组数。

2.2 露天矿边坡稳定系数模型的建立

1）训练样本数据归一化。由于所选取的边坡稳定性影响因素量纲不同，因此各因素之间具有不可共度性，不能进行直接比较，必须把这些量化的因素按某种效用函数归一化到某一无量纲区间。采用线性归一化方法对所选取的6 个边坡稳定性影响因素及边坡稳定系数训练样本数据进行归一化处理。若训练样本数据中第i 个影响因素的最大与最小值分别为ximin与ximax，则归一化后的第i 个影响因素为xi′。设训练样本数据中边坡稳定系数的最大、最小值分别为fsmax、fsmin，则归一化后的第i 个边坡稳定系数为fsi′。

2）应用粒子群算法优化RBF 神经网络模型参数。①确定粒子群算法初始潜在解：采用随机方法确定输入数据的中心向量；②确定粒子群参数值：粒子个数取20，最大迭代次数取100，加速因子c1=c2=1.494 45；③初始化粒子初值和速度，并用适应度函数计算粒子群中各粒子的适应度值；④对每个粒子，比较其适应度与它所经历的最好中心点的适应度，如果更好，则更新Pbest；⑤对每个粒子，比较它的适应度与群体所经历的最好中心点的适应度，如果更好，则更新Gbest；⑥更新粒子的速度与中心点；⑦重复步骤④～步骤⑥，直到适应度值满足结束条件或达到最大迭代次数，返回全局最小适应度值对应的中心点Gbest对应的粒子作为RBF 神经网络参数。

3）RBF 神经网络建立与训练。将经粒子群算法优化得到的全局最小适应度值对应的中心点Gbest作为RBF 神经网络的结构参数，利用MATLAB 神经网络工具箱建立RBF 径向基函数神经网络，将归一化后的6 个边坡稳定性影响因素（边坡岩体密度ρ、黏聚力C、内摩擦角φ、边坡角α、坡高H、孔隙压力比γu）样本值作为网络输入层的输入，对应的归一化后的边坡稳定系数样本fs作为网络输出，对RBF 神经网络进行训练，建立起边坡岩体密度ρ、黏聚力C、内摩擦角φ、边坡角α、边坡高度H、孔隙压力比γu与边坡稳定系数fs之间的非线性映射关系，并储存于网络之中。

4）网络仿真。将待预测边坡的岩体密度ρ、黏聚力C、内摩擦角φ、边坡角α、边坡高度H、孔隙压力比γu数据进行归一化处理，将处理后的数据输入到训练好的RBF 神经网络进行仿真，RBF 神经网络预测出与各组输入数据对应的边坡稳定系数fsi*，将此预测数据按下式进行反向还原，即得到各边坡稳定系数预测值fs：

式中：fs*为RBF 神经网络预测的边坡稳定系数值，fs为反向还原后的边坡稳定系数值。

3 应用实例与结果分析

基于MATLAB 软件平台，编制基于粒子群算法与RBF 神经网络[7]的露天矿边坡稳定系数预测程序PSO-RBF。原始边坡样本数据共45 组，经粒子群算法优化RBF 神经网络参数后，建立RBF 神经网络网络模型，另外5 组样本作为检验数据，用以检验RBF神经网络的泛化能力。另选取6 组边坡数据[8]，分别应用PSO-RBF 神经网络与单纯RBF 神经网络预测边坡稳定系数。

选取其中的40 组边坡样本数据见表1。

边坡稳定系数分析计算值与PSO-RBF 神经网络预测值见表2。

RBF 与PSO-RBF 神经网络边坡稳定系数预测值对比见表3（表中边坡稳定系数计算值是采用二维刚体极限平衡法计算得出）。

由表2（表中边坡稳定系数计算值是采用二维刚体极限平衡法计算得出）可知，PSO-RBF 神经网络预测边坡稳定系数最大相对误差3.02%，最小0.35%，平均误差1.60%，预测精度完全能够满足实际工程需要。

由表3 分析可知，RBF 神经网络预测性能不够稳定，6 组数据中有2 例预测结果误差较大，相对误差已分别达到11.48%和15.10%，PSO-RBF 神经网络预测结果相对比较均衡，相对误差最大仅为2.49%，与单纯的RBF 神经网络方法项目比，PSORBF 神经网络边坡稳定系数预测方法的预测性能更稳定、精度更高。

表1 PSO-RBF 神经网络训练样本数据

表2 边坡稳定系数分析计算值与PSO-RBF 神经网络预测值

表3 RBF 与PSO-RBF 神经网络边坡稳定系数预测值对比

4 结语

1）RBF 神经网络是由大量处理单元组成的非线性大规模自适应系统，其隐层可实现从输入空间到隐空间的非线性变换，对解决诸如边坡稳定系数预测这类复杂非线性问题具有独特的优势。利用粒子群算法全局搜索能力对RBF 神经网络参数进行优化，避免了由于RBF 神经网络参数选取不当对边坡稳定系数预测精度的影响。

2）在影响露天矿边坡稳定的众多因素中，选取了边坡岩体密度ρ、黏聚力C、内摩擦角φ、边坡角α、边坡高度H、孔隙压力比γu等6 个可量化的典型影响因素，建立了基于粒子群算法的RBF 神经网络边坡稳定系数预测模型。

3）实践应用表明，基于粒子群算法与RBF 神经网络预测边坡稳定系数结果可靠，能够满足实际工程需要。与单纯的RBF 神经网络方法相比，PSO-RBF神经网络的预测精度更高，性能更稳定。