粒子群优化最小二乘支持向量机的短期负荷预测研究

陈金菊，涂志达，蔡成鑫，黄敬淋，刘书瑞

（宁德师范学院信息与机电工程学院 福建 宁德 352100）

1 引言

目前电力系统的短期负荷预测正处于由人工经验运算转换到了智能预测时代。国内外负荷预测方法具体有两种方向，一种是较为新型的人工智能预测方法，另一种是相对传统的数学统计预测方法[1-2]。

人工智能类的短期负荷预测方法具有良好的发展前景，在面对非线性的情况时有更好的处理效果。神经网络是智能处理的一种方法，通过不断的学习获得更优的参数，在预测的过程中会随着变化的训练样本自动优化。

2 粒子群优化算法

粒子群算法，对鸟类的群体觅食行为和迁徙群居行为进行研究[3-4]，粒子群算法的主要步骤[4]：

（1）设定粒子个体的最优位置pi=xi以及整个种群的全局最优位置pg，c1和c2是学习因子的参数，d则是空间维度的大小，N是粒子种群数值，vij与xij则是初始任意粒子速度和位置；

（2）根据适应度函数的情况，解出各个粒子的适应数值；

（3）若粒子本身的最优值优于适应值则维持粒子本身的最优值，否则舍弃原本的最优值用适应值进行替代；

（4）通过比较的方式来决定全局最优值；

（5）更新粒子与种群的位置与速度；

（6）更新速度、位置的粒子进行判别，循环直到算法得以满足结束。

3 最小二乘支持向量机

对于最小二乘支持向量机的目标函数[5-6]：

定义拉格朗日函数:

则 LSSVM 非线性预测模型可表示为

4 仿真与分析

以某地区2月1日—2月7日的历史负荷数据为样本，对该地区2月8日的负荷进行预测。粒子群算法寻优后得到的惩罚系数C∈[0.1,150],核函数参数σ∈[0.1,10]，取最大迭代次数为100，种群规模为100。

惯性权重系数w是用来控制粒子以前速度对当前速度的影响，即粒子对以前速度的信赖性，这会使粒子在寻找最优解过程中错过最优解的位置，为了尽可能达到平衡全局和局部搜索的能力，以实现提高效率、减少迭代次数以及加快收敛速度，最终得到最优解，本文通过调试选取权重系数w ∈ [0.15,0.92]。

学习因子c1和c2分别为粒子接近Pibest位置的统计加速权重和粒子接近Gbest位置的统计加速权重，由于c1过大会导致粒子在局部区域内错过最优目标，c2过大会导致粒子过早收敛，通过多次调试，本文选择的学习因子C1=1.3，C1=1.7。

负荷预测值与真实负荷值进行对比，采用相对误差和相对平均误差值来评判误差。图1为第8d负荷预测值与真实值的对比图。

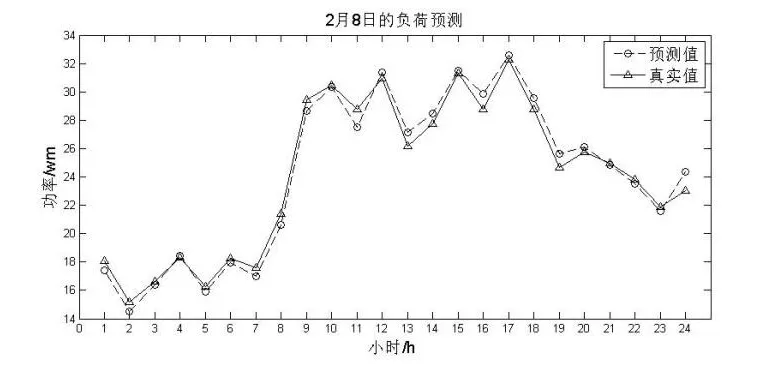
图1 PSO-LSSVM真实值与预测值对比

如图1为2月8日的电力负荷真实值与预测值的平均相对误差为：

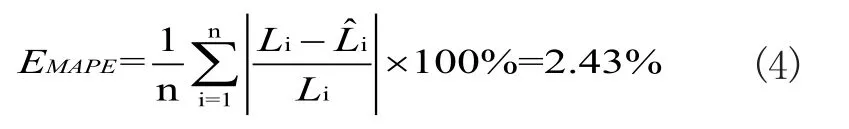
如图1和式(4)可知：粒子群-最小二乘支持向量机的负荷预测的结果，相对误差最大值为EREmax=-5.39%，最小值为EREmin=0.36%，平均相对误差为EMAPE=2.43%，预测精度较高。

5 结语

采用SLSVM模型对短期负荷进行预测，以PSO算法优化SLSVM模型中的惩罚系数C与核函数σ的值，提高了短期负荷预测的精度，具有较广泛的工程应用价值。