考虑荷载作用效应的混凝土中氯离子扩散细观数值模拟

柳子然 ，袁春坤，李世森，王元战

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2.中国路桥工程有限责任公司，北京 100011)

海洋环境中，氯离子侵蚀引起混凝土内钢筋锈蚀，是钢筋混凝土结构发生耐久性破坏的重要原因，且混凝土结构在设计使用基准期内，普遍处于承受荷载作用的状态，有些结构在受荷状态下会形成裂缝。由机理上分析，荷载对混凝土内氯离子侵蚀过程的影响可以分两种[1]：荷载水平较低时，即混凝土在受荷情况下其内应力水平未达到其强度前，混凝土未产生明显裂缝，氯离子侵蚀受外荷载的影响，可以视为由外荷载引起孔隙率的改变对氯离子扩散的影响；当荷载水平较高时，即受荷情况下混凝土形成裂缝，裂缝决定其中氯离子的侵蚀过程。在正常使用荷载水平下，荷载对混凝土中氯离子扩散行为的影响由孔隙率的改变决定。本文针对正常使用荷载水平情况，即荷载作用下混凝土内应力水平未达到其强度前，混凝土中未形成明显裂缝，研究荷载对氯离子扩散过程的影响规律。

氯离子在混凝土内的扩散过程较为漫长，物理试验和数值模拟是研究受荷混凝土中氯离子扩散的两种主要手段。其中物理试验又分为原位测试和室内试验两种。原位测试方面：Kwon等[2]现场观测得出服役7 a与11 a的码头混凝土结构中氯离子扩散系数，通过蒙特·卡罗法预测其耐久性。室内试验方面：Wang等[3]采用自行设计的潮汐循环装置和盐雾室，研究了荷载水平为构件抗折强度的0、0.3和0.5倍时，潮汐区和盐雾区中混凝土构件内氯离子的扩散规律，并建立了考虑荷载水平影响的混凝土内氯离子浓度的预测模型；崔衍强[4]研究了暴露于海洋环境水位变动区与盐雾区内，荷载水平改变对混凝土中氯离子扩散过程的作用，根据其实测值拟合出氯离子扩散系数的荷载影响系数。

相较于数值模拟而言物理实验周期长，耗费物力、财力和人力更多，研究效率较低。通过数值模拟来探求荷载对混凝土中氯离子扩散过程的影响，是种较为快捷且高效的研究方法。在宏观尺度上，即将混凝土视为连续均匀介质，Xiang等[5]采用现象学损伤模型，用条分法模拟混凝土结构的非线性响应，研究疲劳损伤混凝土中氯离子扩散的时变性。Pijaudier-Cabot等[6]采用相似方法，经研究得到荷载水平引起的损伤对混凝土渗透性的影响很大，不可忽略。上述对于该问题的数模研究大多从宏观层面上，把混凝土看作均匀介质，难以体现其细观结构对氯离子扩散特性产生的影响。

混凝土的细观结构由水泥砂浆、骨料与界面过渡区(ITZ)三部分构成，这三者各自特性可能对混凝土中氯离子扩散产生不同影响。为更深入探求受荷混凝土中氯离子的扩散规律，研究者们的研究方式开始由宏观深化至细观。Du等[7]将混凝土视为由水泥浆体、骨料和ITZ及构成的复合材料(其中，骨料不具有渗透能力，氯离子可以在浆体中扩散，ITZ具有较高扩散性)，建立了模拟混凝土氯离子扩散的细观分析计算模型。吴静新[8]模拟了非受荷混凝土在二维细观凸多边形骨料模型中的氯离子扩散模型，及三维宏观混凝土梁受荷时的氯离子扩散过程。何明伟[9]模拟了轴向荷载作用下混凝土在球形粗骨料、ITZ与水泥砂浆组成的三维细观模型内的氯离子扩散过程，对不同应力水平中，混凝土单轴受拉时其内氯离子扩散情况进行了分析：应力水平较低时，混凝土中的轴向拉应力对氯离子扩散的作用可忽略；在高应力水平中，裂缝的产生会对氯离子扩散产生较大影响。

当前，多数学者主要结合有限元数值模拟的手段建立混凝土的二维模型来分析荷载对混凝土内氯离子扩散过程的作用，少量三维细观模型也重点模拟轴向荷载对混凝土立方体中氯离子扩散的影响。而在服役期内多数海工钢筋混凝土构件的受力环境也不仅是单轴(拉、压)荷载作用的单一状态。因此，建立混凝土构件的三维数值模型，进一步分析其他荷载形式的影响(如：氯离子在受弯混凝土梁构件中的扩散规律)，对研究混凝土耐久性有一定意义。

本文采用数值模拟的手段，将混凝土视为由固化水泥砂浆、碎石粗骨料、固化水泥砂浆与粗骨料之间的界面过渡区构成的复合材料，认为氯离子传输扩散行为只发生在固化水泥砂浆和界面过渡区中；基于荷载作用使混凝土孔隙率发生变化、进而导致氯离子扩散系数变化的假设，提出了考虑荷载作用效应的混凝土中氯离子扩散系数模型。进而建立受荷混凝土中氯离子扩散细观数模模型，并与物理试验实测值对比验证了此细观数模结果。通过对受荷简支梁氯离子扩散细观数值模拟，分析了荷载水平对氯离子扩散规律的影响，为研究荷载作用下混凝土氯离子扩散特性提供了一种有效手段。

1 混凝土细观组成

图1 混凝土细观物理分析模型Fig.1 Meso-scale physical analysis model of concrete

在混凝土构件有限元细观分析里，首先应建立合理混凝土细观模型。在细观尺度上，混凝土被概化成三相复合材料[10]，即粗骨料、界面过渡区(ITZ)和水泥砂浆，ITZ是附着在粗骨料表层的可供氯离子传递的均匀介质，使粗骨料简化成圆，混凝土三相细观模型如图1所示。

1.1 水泥砂浆

水泥砂浆是一种典型的多孔复合材料，由水泥、水和细骨料组成，其力学特性可视为弹性均质体，而其中有许多微裂缝与毛细管孔隙结构，因此可供氯离子在其中传递。

1.2 粗骨料

粗骨料是可有效提升混凝土结构力学性能的组成材料，亦为混凝土内不能被氯离子通过的主要材料，即粗骨料内氯离子扩散系数约等于0。混凝土非均匀性的主要原因即为粗骨料在水泥砂浆中含量与随机分布[11]，其会影响混凝土中毛细管孔隙率与细观结构，其中氯离子的扩散机能也随之改变[12]。研究证实[13]，混凝土内氯离子传递受粗骨料影响有3种表现：曲折、稀释与界面过渡区(ITZ)效应。曲折和稀释效应使混凝土中氯离子的扩散系数降低，而ITZ效应相反[14]。

(1)稀释效应。

粗骨料的致密性远大于水泥砂浆，因此可将其视为不能被氯离子通过的不可扩散介质。若在原可扩散介质(即水泥砂浆)中掺入更多粗骨料，将导致混凝土中可扩散材料的比例减少，混凝土整体的氯离子扩散系数变小，即稀释效应。基于此效应，受粗骨料体积分数影响的混凝土内氯离子扩散系数为[15]

DD=D0(1-v)

(1)

式中：DD为基于稀释效应的混凝土内氯离子扩散系数；v为粗骨料体积分数；D0为水泥砂浆的氯离子扩散系数。

(2)曲折效应。

氯离子不能穿过粗骨料进行传递的现象表明粗骨料会使氯离子扩散路径变长，降低氯离子扩散系数，即曲折效应。基于粗骨料的曲折及稀释效应，受粗骨料体积分数影响的混凝土内氯离子扩散系数为[16]

DT=D0(1-v)3/2

(2)

式中：DT为基于曲折及稀释效应的混凝土内氯离子扩散系数。

(3)界面过度区效应。

水泥的水化反应会使混凝土的水泥基与骨料间产生一层有别于水泥基的微观结构，其厚度较小(通常不超过100 μm)，但Ca(OH)2含量与孔隙率更大，被称为界面过渡区(interfacial transition zone，简称ITZ)[17]。ITZ内孔隙率比水泥砂浆更大，故其氯离子扩散系数比水泥砂浆氯离子扩散系数更大，使得仅考虑粗骨料的稀释和曲折效应的参考氯离子扩散系数相较试验拟合出的结果偏小，即界面过渡区(ITZ)效应[18-19]。

1.3 界面过渡区

Nilsen和Monteiro[20]发现：如果仅假设混凝土是由粗骨料和水泥砂浆组成的复合材料，不考虑ITZ，其数模结果与试验实测值有差别，不能用以研究混凝土结构耐久性。为探求ITZ参考氯离子扩散系数，将粗骨料看作粒径不一的三维球体，且其表面有层均匀等厚的薄膜，即ITZ，如图1所示。综合粗骨料的曲折、稀释和ITZ效应，混凝土参考氯离子扩散系数如式(3)所示[14]

D28=D0(1-v)3/2+(DITZ-D0)vI

(3)

式中：D0为水泥砂浆中氯离子扩散系数；DITZ为ITZ氯离子扩散系数；v为粗骨料体积分数；vI为界面过渡区体积分数。D0(1-v)3/2反映粗骨料曲折、稀释效应， (DITZ-D0)vI反映ITZ效应。

Wang[21]等基于试验，分析了粗骨料体积分数v对DITZ的影响。结合式(3)，可推出DITZ与v的关系如式(4)所示

(4)

式中：h为ITZ厚度；v为粗骨料体积分数；da为粗骨料平均粒径。

2 受荷混凝土内氯离子扩散系数

荷载作用使混凝土微观结构变化(如裂纹扩展、孔隙率变化等)，引起混凝土的抗侵蚀性能改变。当受荷混凝土中应力在其强度范围里时，混凝土未产生新裂缝，荷载对氯离子扩散的影响可看作荷载使孔隙率改变影响了氯离子扩散。因此将受荷混凝土体积应变和孔隙率作为荷载场与氯离子扩散间的参数变量，其氯离子传输数值模拟逻辑如图2所示。

图2 外荷载作用下混凝土内氯离子扩散数值模拟思路Fig.2 Numerical simulation of chloride diffusion in concrete under external load

混凝土的孔隙率φ即混凝土中孔隙体积与混凝土总体积的比值，当混凝土因受荷产生形变后，其内孔隙率φ为[8]

(5)

式中：εv为混凝土的体积应变；φ0为混凝土的初始孔隙率，如下式所示[25]

(6)

式中：w/c为混凝土水灰比；α为水化度，取值区间为(0.3,0.9)[22]，根据水灰比为w/c=0.38，考虑混凝土在实验室经28 d养护后的水化程度较好水化度取α=0.9，则初始孔隙率为φ0=0.224。

用选取常用的氯离子扩散系数的时变模型，将基准时间统一为28 d，则氯离子扩散系数时变模型表示为

表1 混凝土龄期系数m取值表Tab.1 Concrete age coefficient values of m

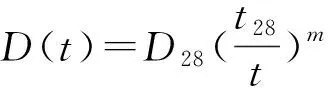
(7)

式中：D(t)为t时刻的氯离子扩散系数；D28为基准时间为28 d的氯离子扩散系数；m为龄期系数，其取值同混凝土材料性质及位置相关，如表1所示[23]。

混凝土的渗透特性取决于其中可供氯离子通过介质的孔隙率，现有文献得到了氯离子扩散系数和水泥浆体孔隙率的量化关系[11,24-25]。Zheng等[11]基于有效介质理论，将硬化水泥浆体看作由液相、固相构成，得到了水泥浆体中氯离子扩散系数的解析解，如式(8)所示

(8)

式中：Dp为硬化水泥浆体孔隙溶液中的氯离子扩散系数，取1.07×10-10m2/s[11,26]；φ为水泥砂浆孔隙率，n为待定参数。

Xu[27]结合混凝土细观结构，用上式(8)表示水泥砂浆中氯离子的扩散系数与孔隙率的关系，并在二维平面中进行了氯离子在受荷混凝土内氯离子扩散的数值模拟，其数值模拟结果与实验数据吻合良好，证明了式(8)在受荷混凝土内氯离子扩散数值模拟的可靠性。

结合氯离子扩散系数时变性，将式(8)Dcp代入式(7)中的D28，得到同时考虑受荷混凝土内孔隙率改变与氯离子扩散时变特性影响的氯离子扩散系数表达式，如下

(9)

式中：待定系数n为与D28所对应的拟合回归参数。

3 混凝土细观数值模型

混凝土材料不均匀性主要是由于其内粗骨料的随机分布和含量不同所引起[28]。通过MATLAB编写随机生成及投放粗骨料的算法程序，建立了混凝土三维球形骨料模型[29]。

3.1 混凝土梁随机骨料模型生成过程

将混凝土中的粗骨料简化为球形，通过MATLAB建立随机生成及投放混凝土球形骨料的程序，要明确混凝土几何参数、粗骨料体积分数、ITZ厚度hITZ、骨料最大粒径与最小粒径，接着基于理想Fuller级配曲线生成随机的骨料粒径，并按条件将骨料投放到混凝土模型中，完整过程为：

(1)混凝土试件的三维尺寸X、Y、Z、粗骨料最大粒径dmax、最小粒径dmin、体积分数v和ITZ厚度hITZ与实验值保持一致。

(2)粗骨料总体积如式(10)所示

V=X×Y×Z×v

(10)

(3)为了令混凝土内粗骨料粒径符合连续级配曲线的累积筛余百分率标准，基于Monte-Carlo法在[0,1]范围中随机生成一个数Fi，使P(d)=Fi，可得与Fi相应的骨料粒径di，随机分布的di满足Fuller级配曲线，骨料的累积分布函数如式(11)所示。

(11)

(4)判断随机生成的di满不满足dmin≤di≤dmax，如不满足，返回上一步重新生成di；如满足，继续下一步。

(5)计算已生成的全部i个球形粗骨料总体积表达式为

(12)

(6)判断已生成的球形粗骨料总体积满不满足Vi≥V，若满足条件，则停止运算，并保存全部数据；如不符合，应到第3步再次得出新骨料，依次进行第4、5、6步，直至条件成立。

(7)将上一步得到的骨料粒径从大到小排序，并依据下列条件从大到小依次投放。

为了令模型内骨料分布符合实际情况，基于Kreijger[29]的实验结果，混凝土表面0.1 mm中没有骨料，0.1～5 mm中骨料比例较小，5 mm以里的骨料在水泥砂浆中随机存在。本文考虑Kreijger[30]的研究结论，并进行简化：在混凝土外层0～3 mm中不含骨料，3 mm以里骨料在其中随机投放，是以骨料球心坐标(xi,yi,zi)须符合下式

(13)

在满足式(13)的区间范围内，基于Monte-Carlo法随机生成第i个骨料球心坐标，不能与已经成功投放的前i-1个球形粗骨料重叠。若符合条件，则将第i个球形粗骨料投放到混凝土细观数值模型当中，并保存(xi,yi,zi)的结果；若不符合条件，重新生成第i个球心坐标，判定是否存在重叠，直到符合条件为止。判别骨料是否重合的表达式如下

(14)

式中：{Li}表示第i个球心距前面i-1个球心的空间向量，其中Li,1、Li,2、…、Li,i-1分别是第i个骨料球心与第1、第2、…、第i-1个骨料球心间的间距；hitz是界面过渡区厚度。

(8)保存骨料粒径及球心坐标。

3.2 建立三维混凝土梁球形骨料模型

依照以上步骤，建立100 mm×100 mm×400 mm混凝土试件，其他相关参数如下设置：dmax取27.5 mm、dmin取 5 mm、体积分数v取0.3、hitz取40 μm，三维混凝土梁球形骨料随机分布模型如图3所示。

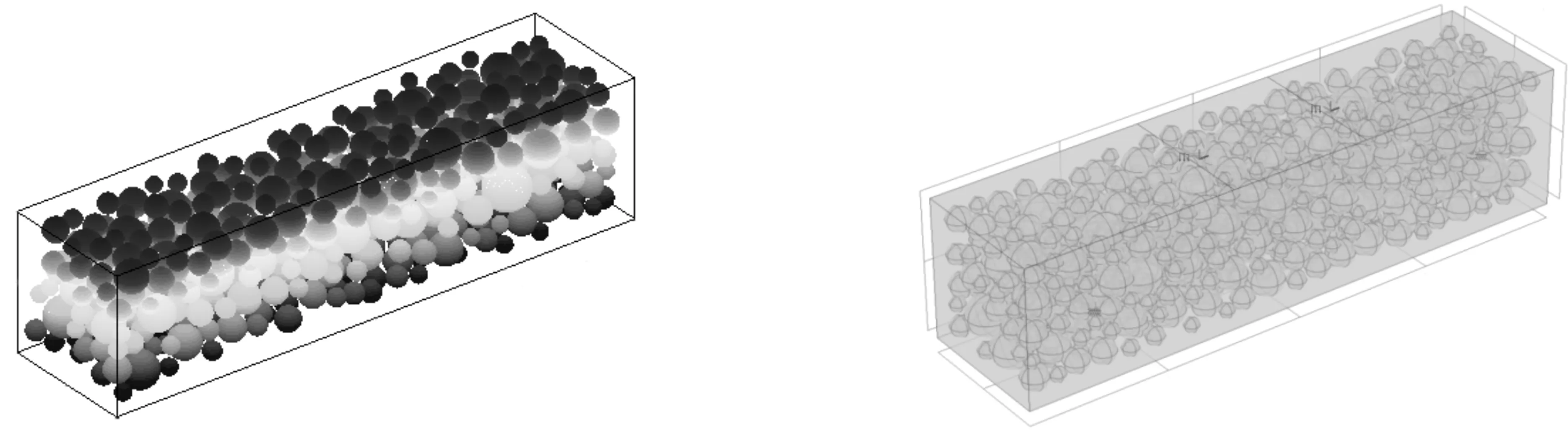
图3 混凝土梁的三相细观结构Fig.3 Three-phase meso-structure of concrete beam图4 三维细观混凝土梁模型Fig.4 3D meso-model of concrete beam

将通过混凝土梁三维球形随机骨料模型获得的骨料信息，将数据导入到有限元软件COMSOL Multiphysics 5.3a中，利用COMSOL内App开发器模块，编写Java程序，得到混凝土梁的三维细观数值模型。基于COMSOL Multiphysics 5.3a中的固体力学模块(solid)模拟混凝土的受力情况，本文为研究受弯混凝土构件，选用线荷载来模拟实验的荷载形式，将中性层与支座界面的交线固定作为简支梁的约束方式，模型建立结果如图4所示。用稀物质传递模块(tds)模拟混凝土内的氯离子扩散过程，tds模块中的控制方程为Fick定律，如式(15)所示，故本模块可模拟混凝土内氯离子的扩散过程。

(15)

4 细观数模结果验证与分析

4.1 试验介绍

崔衍强[4]为研究荷载对混凝土中氯离子扩散的影响，试验制作了100 mm×100 mm×400 mm的素混凝土梁试件。实验主要材料参数如下：标号42.5的普通硅酸盐水泥，石子用碎石，沙子为河砂(中砂)，取水灰比为0.4，材料用量如表2所示。试件制作过程如下：(1)制作试件养护28 d；(2)用环氧树脂把5个面密封，剩余一个400 mm×100 mm面作氯离子侵蚀面；(3)用三分点自锚加载法做为加载形式，将抗折强度的50%和30%作为实验荷载，分别模拟受弯构件中的受拉区(用T表示)和受压区(用C表示)。

表2 混凝土材料表Tab.2 Concrete material

试验模拟荷载作用下干湿循环区混凝土的氯离子扩散情况：将加载好的试件置入人工海洋潮汐循环自动化模拟试验装置，取浓度3.5%的氯化钠溶液模拟海水，干燥12 h、浸泡12 h反复循环。当30 d、70 d、120 d时，拿一个试件，钻直径10 mm圆柱作样本，每5 mm分层磨得混凝土粉，并使其通过0.63 mm筛子，随后烘干，最后其浓度利用氯离子含量快速测定仪测得。

4.2 参数选取

为了确保基于有限元数值模拟计算结果的合理性和可靠性，在建模过程中应保证混凝土细观数值模型的初始条件、边界条件、氯离子扩散系数等相关参数设置正确、取值合理。

表3 材料参数表Tab.3 Material parameters

(1) 初始条件：制作混凝土使用的材料均无氯离子存在，合理假设其内氯离子初始浓度取0，即C(x,0)=0。

(2)边界条件：试验里，试件5个面密封，故数值模拟时设为无通量属性；试件一个面作为侵蚀面，根据崔衍强[4]的实验结果，考虑表面氯离子浓度Cs的时变特性，用Origin软件进行处理，侵蚀面氯离子浓度为

Cs(t)=0.894 5+0.149 8ln(t)

(16)

式中：t为扩散时间，单位是年。

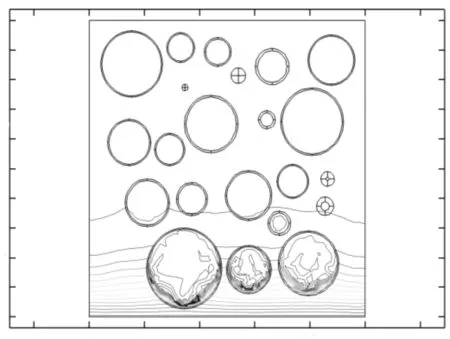
图5 混凝土氯离子浓度分布图Fig.5 Distribution diagram of chloride concentration

(3)初始孔隙率。根据公式(6)，试验混凝土的水灰比0.38，认为试验混凝土水化程度良好，水化度取0.9，带入公式(6)，得到初始孔隙率φ=0.32。

(4)氯离子扩散系数。其中水泥砂浆中氯离子扩散系数根据公式(9)进行设置，龄期系数根据表1，取普通硅酸盐混凝土在潮汐区的值m=0.37，由试验实测值[5]可拟合得到混凝土第28 d氯离子扩散系数D28，根据式(3)可求得水泥砂浆的扩散系数D0，式中待定参数经拟合得n=0.408。基于式(4)可得到ITZ中氯离子扩散系数为水泥砂浆中的24.805倍。粗骨料中氯离子扩散系数为0。

(5)相关其他参数，如表3所示[27]。

4.3 混凝土内氯离子扩散数值模拟结果及验证

以受拉区荷载水平0.3、扩散70 d通过tds模块模拟得到结果举例，氯离子扩散情况如图5所示。

利用Origin处理细观数值模拟结果和物理试验实测结果进行对比(C表示受压区，T表示受拉区)，具体结果如图6所示。

6-a 0.5 C6-b 0.5 T

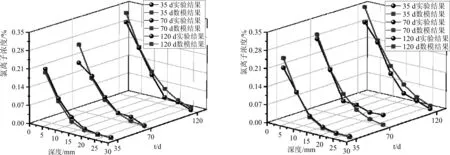
6-c 0.3 C6-d 0.3 T

6-e 无荷载图6 氯离子浓度分布对比图Fig.6 Comparison chart of chloride ion concentration distribution

误差分析情况如图7所示。对细观数值模拟结果与试验结果的有效数据点比较分析可得，采取受荷混凝土梁细观模型的数值模拟方法得到的氯离子浓度值分布与物理试验实测值的数值大小及变化趋势均基本吻合，忽略浓度值较小的点，二者的相对误差基本包含在±30%的范围内，35 d、70 d、120 d数模与试验结果相比平均误差分别为19.2%、15.8%、13.3%。因此，利用有限元计算受荷混凝土细观模型内氯离子扩散数值模拟有其可行性与可靠性，可将本细观数模手段用来预估海洋环境下考虑荷载作用效应的混凝土结构物内氯离子扩散情况。

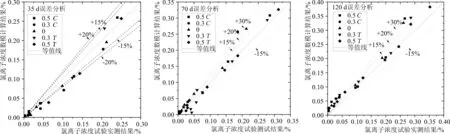
7-a 35 d7-b 70 d7-c 120 d图7 宏观数值模拟误差分析图Fig.7 Macro numerical simulation error analysis chart

图8 混凝土应力分布图Fig.8 Stress distribution diagram of concrete

4.4 混凝土受力情况数值模拟结果及分析

为了验证细观数值模拟手段模拟荷载作用可行，以荷载水平0.3的应力模拟情况举例分析，调整颜色范围即应力最低值取0时，能明显区分受压区与受拉区，与简支梁的受力情况相符，如图8所示。

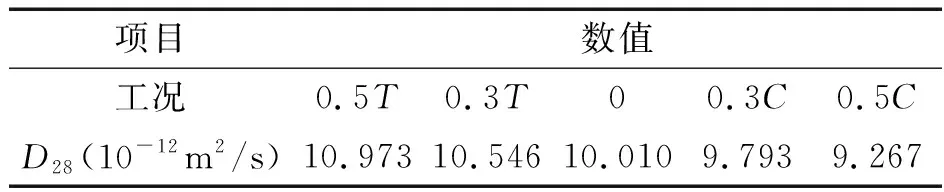
表4 第28 d氯离子扩散系数Tab.4 Chloride diffusion coefficient at the 28th day

利用Fick第二定律处理数模计算出的不同荷载水平下混凝土内氯离子扩散的浓度分布，可得其受荷混凝土28 d氯离子扩散系数，如表4所示。对其进行观察发现，混凝土内氯离子扩散受荷载影响明显，受拉区混凝土的扩散系数随荷载水平的增大而增大，而受压区则相反。究其原因，是荷载作用改变了混凝土中的应力、应变，混凝土孔隙率又受应变影响，即受压区混凝土在荷载水平增大时，其内应力、应变增大，导致孔隙率减小，氯离子扩散系数随之减小；而受拉区反之同理。

5 结语

本文用荷载作用下混凝土中氯离子扩散细观数值模拟手段，建立了考虑荷载作用效应的混凝土内氯离子扩散预测模型，主要结论有：

(1)本文假定在设计外荷载作用下，即混凝土中未产生新裂纹时，外荷载对混凝土中氯离子扩散行为的影响，可视为荷载所引起孔隙率的改变影响了氯离子扩散性能。鉴于此，通过孔隙率与外荷载(以体积应变来表征)之间的定量关系，建立了受荷混凝土内的氯离子扩散系数(主要受孔隙率影响)与外荷载之间的定量关系。

(2)将COMSOL多物理场耦合算法与受荷混凝土内氯离子扩散的数值模拟手段结合，提出了考虑荷载作用效应的混凝土内氯离子扩散的细观数值模拟方法。

(3)结合不同理论与多个试验结果，建立了混凝土第28 d氯离子扩散系数与水泥砂浆的氯离子扩散系数的关系，以及ITZ与水泥砂浆中氯离子扩散系数的关系，使得数值模拟的适用性更高，即在已知粗骨料体积分数的情况下，通过实测数据得到混凝土第28 d氯离子扩散系数或者水泥砂浆的氯离子扩散系数，便可以利用本文的数值模拟方法对受荷混凝土内氯离子扩散进行细观上的数值模拟。

(4)将受荷混凝土梁细观数模计算情况与对应的物理试验的实测值做比较，结果较为吻合，验证了受荷混凝土梁中氯离子扩散细观数值模拟方法的合理性。